带有耗散梯度函数的抛物方程爆破与有效性分析

凌征球, 何 冰

(1.玉林师范学院 数学与统计学院, 广西 玉林 537000; 2.吉林大学 数学学院, 长春 130012)

0 引 言

在混合边界条件下考虑下列带有耗散梯度函数的抛物方程解的爆破问题:

(1)

其中：Ω是3维空间3中具有凸性和光滑边界∂Ω的一个有界区域;p,m,a>0,q>2; Δ和分别表示Laplace算子和梯度算子;T表示可能的爆破时间; (∂u/∂ν)表示在边界∂Ω向外的法向单位导数;u0(x)为平凡有界、 适当光滑的非负函数.形如问题(1)的非线性抛物方程在热传导与种群动力系统等领域应用广泛[1-2].目前, 关于非线性抛物方程解的爆破分析已得到广泛关注, 多种抛物方程解的爆破时间下界已被确定[3-7].Li等[8]在齐次Dirichlet边界条件下研究了问题(1)的爆破现象, 借助Sobolev与一阶微分不等式得到了爆破时间的下界估计.本文在混合边界条件下扩展文献[8]的工作, 由于边界条件不同, Sobolev不等式将不再可用, 当方程的解发生爆破时, 通过建立一些合适的Sobolev型不等式, 给出爆破时间的下界估计, 进而给出下界估计的有效性分析.

1 主要结果

假设问题(1)的每个正解除了在某些时刻可能发生爆破外都是古典解, 本文考虑当m,p>1时如果问题(1)的解在有限时刻T发生爆破, 建立T的下界估计.为此, 定义辅助函数

(2)

其中k>max{8m-9,16m-8q-9,8p-q,3q-4}.利用Green公式, 可得

(3)

为讨论方便, 令v=u(k+q)/q, 则根据Höder和Poincare不等式, 得

(4)

(5)

这里λ1是下列弹性膜问题的第一正特征值:

于是, 从混合边界条件, 式(5)可变成

(6)

(7)

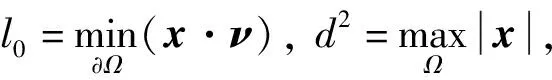
(8)

这里θ是任意正的常数.由式(6),(8), 有

(9)

(10)

(11)

从而式(3)变为

(12)

由于式(12)的右边有两项含有梯度函数, 下面用两种方法计算当爆破发生时爆破时间的下界估计.

1.1 方法1

下面通过计算第一项抵消第三项.类似于式(7),(8), 得

因此,

(13)

其中μ1是一个正的常数.把式(13)代入式(12), 并选择μ1满足d(k+m)μ1-2kl0=0, 得

(14)

下面分别估算J1,J2,J3.

1)估算J1.根据Hölder不等式与arbs≤ra+sb,r+s=1,a,b>0, 可得

(15)

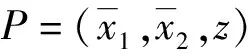
从而

(16)

类似地, 有

(17)

将式(16),(17)相乘并在Dz上积分, 得

(18)

将式(18)代入式(15)得

(19)

其中

(20)

为了计算式(19)中ω3在Dz上的积分, 把区域Ω在截面Dz上面的部分与边界分别记为Ω+和∂Ω+, 下面的部分相应记成Ω-和∂Ω-.于是由散度定理得

从而

(21)

再利用Schwarz不等式, 有

由式(21)得

(22)

类似式(7),(8), 有

(23)

再由Young不等式(a+b)3/2≤21/2(a3/2+b3/2),a,b>0, 则式(22)可变为

(24)

这里ε1是一个任意的正常数.再根据Hölder不等式, 有

(25)

因此, 根据J1的定义, 并结合式(24),(25), 且选择ε1满足

可得

(26)

(27)

采用上述分析方法计算函数u9(k+q)/8的积分, 可得类似式(24)的不等式:

(28)

其中ε2是一个任意正的常数.将式(28)代入式(27)并选择ε2满足

可得

(29)

(30)

(31)

其中：

(32)

定理1如果p,m>1,τ1>0, 则对于每个按测度式(2)在时刻T爆破的非负古典解u,T有下界估计式(32).

1.2 方法2

下面通过计算式(12)的第一项抵消第四项.类似于式(13), 可得

(33)

(34)

类似前面估算J1,J2,J3的方法, 可得

其中:

将式(35)～(37)代入式(34), 即可得关于函数φ的一阶微分不等式:

φ′(t)≤K4φ(t)+K5φ(t)9/8+K6φ(t)3/2,

(38)

其中:

于是可得爆破时间T的下界估计:

(39)

综上, 有:

定理2如果p>1,m>(q+1)/2,τ1>0, 则对于每个按测度式(2)在时刻T爆破的非负古典解u,T有下界估计式(39).

2 有效性分析

下面分析定理1和定理2的有效性, 即讨论下界估计式T1和T2哪个更趋向于爆破时间T.根据定理1和定理2的条件, 当p>1, 11,m>(q+1)/2.

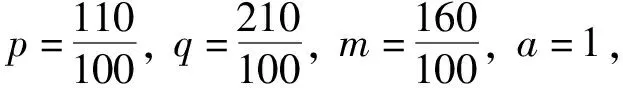
显然l0=1,d=1, |Ω|=1,k>6.7.此外, 为了简化计算, 假设第一特征值λ1和常数θ满足：

λ1-3a(k+q)/(2l0)=1,C1=[λ1-3a(k+q)/(2l0)]-ad(k+q)θ/(2l0)=1/2.

根据上述分析得到的计算公式, 经过计算可得定理1和定理2的相关数据，分别列于表1和表2.

表1 定理1的相关数据

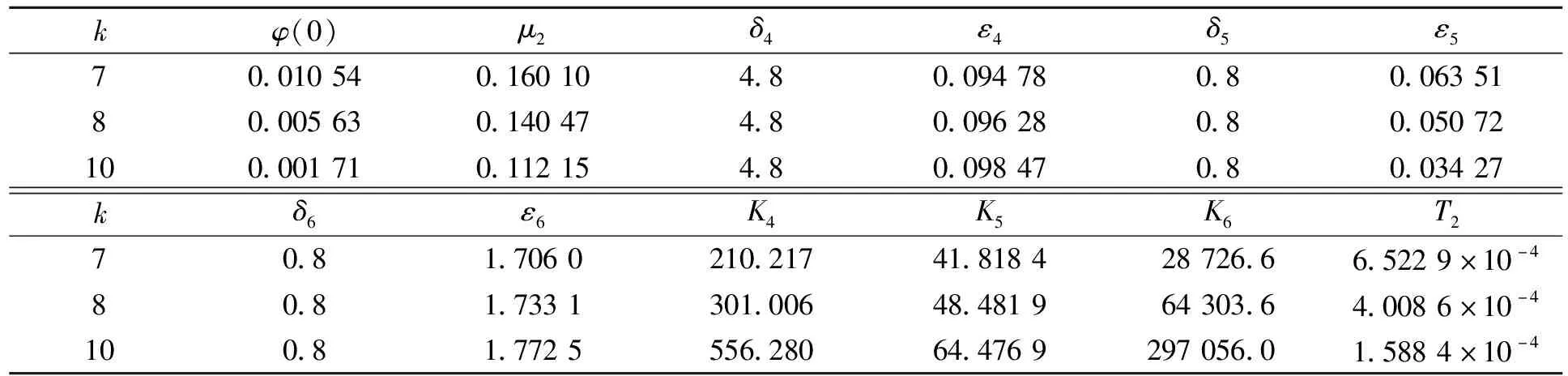
表2 定理2的相关数据

首先, 对于固定的参数k, 由表1和表2可见, 爆破时间的下界T1和T2满足T1