基于可辨识集消解策略的覆盖决策系统约简算法

林荣德， 李进金,2， 陈东晓， 黄建新， 施晗娟

(1. 华侨大学 计算科学福建省高校重点实验室 数学科学学院 福建 泉州 362000； 2. 闽南师范大学 数学与统计学院 福建 漳州 363000)

0 引言

特征选择或属性约简是数据挖掘及机器学习中一种重要的数据预处理方法。在信息系统中数据对象的性质是通过一系列属性表达的，而其中部分属性可能与对象的性质无关。属性约简就是去除与保持某种分类性质无关的属性的过程。由Pawlak提出的粗糙集理论[1-2]作为一种重要理论工具在属性约简、规则提取、数据挖掘和知识发现中得到了多种应用。经典粗糙集通常只适合处理离散型的数据，当处理连续数值型数据时需要先将其离散化，该操作会造成信息损失，因此邻域粗糙集方法[3]被提出并运用于处理连续数值型数据和离散型数据的属性约简[4-10]。近年来，对连续数值型数据以及信息缺失的数据采用基于覆盖粗糙集[11-13]的方法进行属性约简等方面的研究也已有许多研究成果[14-22]。

对象之间的可辨识集是指形成它们之间的可辨识关系所依赖的属性、特征或其他要素等所构成的集合。Skowron和Rauszer[23]建立了基于可辨识关系的属性约简理论框架。Yao等[24]提出通过属性重要度将辨识矩阵转化为最简辨识矩阵从而得到属性约简的方法，但未给出得到各属性重要度的方法。葛浩等[25]研究了信息粒度和辨识能力的关系，通过计算各属性之间的相对辨识能力直接从信息系统得到约简属性集。杨蕾等[26]研究了在序决策系统中用辨识函数构造一种树型结构，并利用其优势关系的分配性质得到约简集的启发式算法。 陶玉枝等[27]研究了基于辨识矩阵的属性约简问题与集覆盖求解问题的等价性，扩展了辨识矩阵的求解方法。在高效构造辨识集的研究方面，杨涛等[28]提出了辨识矩阵的压缩表示方法及相应属性集求核算法。 Wei等[29]和Ma等[30]分别研究了动态数据集中属性增加时用增量法构造辨识矩阵的问题，以及采用压缩的布尔向量来存储对象的可辨识集的属性约简算法。Chen等[31]研究了在覆盖决策系统中建立对象之间的超链接图来表达可辨识关系并进行属性约简的算法。此外，在不协调信息系统、序决策信息系统和概念格的属性约简中高效构造辨识矩阵的问题等方面的研究有了启发性的结果[32-34]。但上述工作主要针对可辨识集的构造方法，或根据属性之间的条件信息熵及相对优势关系确定属性重要度等问题。

为了进一步挖掘覆盖决策系统的可辨识集中所包含的信息来获取约简集，本文首先根据覆盖决策系统协调覆盖集与可辨识集簇之间的联系，提出覆盖在可辨识集簇中的相对辨识能力的概念，给出相对辨识能力下的覆盖核心集的相关性质。接下来给出可辨识集簇在给定覆盖下进行消解操作的定义，得到提取最大辨识能力的覆盖，然后对可辨识集簇进行消解的逐次“提取-消解”的迭代，直到可辨识集簇被完全消解最终得到约简覆盖集，同时对算法的正确性和计算复杂性进行分析。最后将若干UCI数据集转化为覆盖决策系统，并运用本算法进行了属性约简实验，验证了所提出算法的有效性。

1 覆盖决策信息系统相关概念

本文的论域U={x1,x2,…,xn}为有限集,C={K1,K2,…,Kn}为U的幂集的一个子集。如果C上每一个集合K均为非空，且满足∪{K|K∈C}=U，则称C为U上的一个覆盖。以下给出来自于文献[11]和文献[15]的覆盖粗糙集相关定义和定理。

定义1[11]设C为U上的一个覆盖，即∪{K|K∈C}=U,对于任意x∈U，令(x)C=∩{K∈C|x∈K},则称Cov(C)={(x)C|x∈U}为覆盖C所诱导的一个覆盖。

定义2[11]设A为U上的一簇覆盖，B={C1,C2,…,Cm}⊆A，对于任意x∈U，称

(x)B=∩{K|x∈K,K∈Ci,i=1,2,…,m}

为x在覆盖簇B下的邻域。并称覆盖Cov(B)={(x)B|x∈U}为覆盖簇B诱导的U上的一个覆盖。

定理1[11]对于任意B⊆A，x,y∈U有性质

1)y∈(x)C当且仅当(y)B⊆(x)B； 2) (x)B=∩C∈B(x)C； 3) (x)A⊆(x)B； 4) (x)B=(x)Cov(B)。

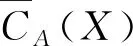
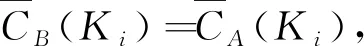
给定(U,A,D)的决策覆盖D={K1,K2,…,Km}，对于任意Ki∈D，根据定义3有

因此下近似约简集的求解可以按照上近似约简集的求解方法进行。本文以下内容仅考虑上近似协调覆盖集或约简集，并记Core(A,D)为上近似核心覆盖集。

定义5[15]设(U,A,D)为覆盖决策信息系统，对于任意x,y∈U，x相对于y的可辨识集

并称L={d(x,y)|d(x,y)≠∅，x,y∈U}为覆盖决策信息系统(U,A,D)的可辨识集簇。

定理2[15]设L为(U,A,D)覆盖决策信息系统的可辨识集簇，则有性质1)、2)：

1)B为(U,A,D)的协调覆盖集，当且仅当对于任意d(x,y)∈L，有B∩d(x,y)≠∅;

2)C是(U,A,D)的核心覆盖元C∈Core(A,D)，当且仅当存在d(x,y)∈L,d(x,y)={C}。

定理2在覆盖决策信息系统(U,A,D)的协调覆盖集与对象之间的可辨识关系中建立了一种联系。其中1)指出了覆盖决策信息系统(U,A,D)的可辨识集簇L中每个可辨识集d(x,y)必定包含协调覆盖集B⊆A中的某些覆盖，这说明出现在可辨识集d(x,y)中的某些覆盖对于辨识对象x、y所起的影响。而2)则进一步强调了约简覆盖集B⊆A中的核心覆盖对于辨识集d(x,y)非空的重要性。

2 覆盖的辨识能力及可辨识集的消解

本节内容将给出一种覆盖C∈A相对于可辨识集簇L的辨识重要度和辨识影响度，以及覆盖C∈A在可辨识集簇L上的消解等概念及相应性质。

定义6给定可辨识集簇L={d1,d2,…,dm}，其中每一个di表示覆盖决策信息系统(U,A,D)中一个非空可辨识集d(x,y)≠∅，对于任意覆盖C∈A，d∈L，记

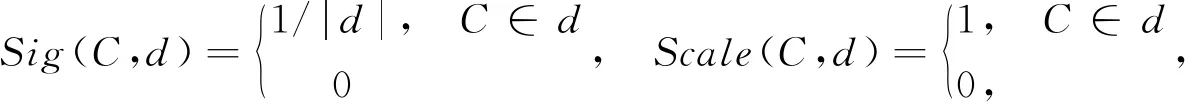
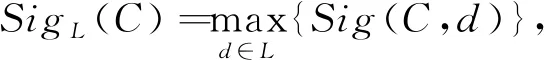
令CapL(C)=(SigL(C),ScaleL(C)), 称CapL(C)为覆盖C相对于可辨识集簇L的辨识能力(简称覆盖的辨识能力)，并记Cap(L)={CapL(C)|C∈A}。

定义7给定任意两个覆盖C1和C2相对于L的辨识能力CapL(C1)=(SigL(C1),ScaleL(C1))和CapL(C2)=(SigL(C2),ScaleL(C2))，则CapL(C1)≥CapL(C2)当且仅当SigL(C1)>SigL(C2)，或，SigL(C1)=SigL(C2)且ScaleL(C1)≥ScaleL(C2)，并记max(L)={C∈A|CapL(C)≥cap,∀cap∈Cap(L)}，表示L中具有最大辨识能力的覆盖构成的集合。

从上述定义6可知，如果L中某个可辨识集是由单覆盖C组成的单点集时，则CapL(C)=1，因此定理2中的2)在可辨识集簇L的重要度上也得到了保证，由定理3给出。

定理3设(U,A,D)的可辨识集簇L是根据定义5所构造的，则覆盖C∈Core(A,D)当且仅当CapL(C)=1。

证明略

定义8给定覆盖C∈A和可辨识集簇L={d1,d2,…,dm}，其中每一个di表示在(U,A,D) 中一个非空可辨识集d(x,y) ≠∅。设LCL是所有包含覆盖C的可辨识集构成的集合，即LC={d|d∈L,C∈d}，则称Diss(L,C)=L-LC是覆盖C∈A对L中的可辨识集的消解，并称V=Diss(L,C) 为C对L消解的结果。

定义8描述了通过给定覆盖C来清除原可辨识集簇L中所有包含覆盖C的可辨识集，因此经过一次消解运算后得到的可辨识集簇V将不含有覆盖C的任何信息，原来的可辨识集簇L规模也严格缩小了，即有V⊂L。

由定义8可看出，如果可辨识集簇V含有核心覆盖，则它在新可辨识集簇V中重要度仍然不变。即这些核心覆盖不被消解过程所去除，可由定理4给出。

定理4给定(U,A,D)的可辨识集簇L，V为可辨识集簇L在某个覆盖C′下的消解结果：V=Diss(L,C′)，则当C≠C′时，如果SigL(C)=1, 则SigV(C)=1。

证明根据定义8中的一次消解操作的过程可以得到，如果L中有一个由单覆盖C(满足C≠C′)组成的可辨识集d={C}，则d不可能被覆盖C′对L的消解操作所去除，仍存在于消解后的结果V中。再由定义6有关覆盖相对于可辨识集簇的重要度定义可得结论成立。

3 基于可辨识集消解策略的覆盖约简算法

由定义6～8，以及定理3和定理4可得到基于“求协调集-去冗余”二阶段求约简集的算法，如算法1所示。

算法1基于可辨识集消解策略的覆盖决策信息系统(U,A,D)的约简算法。

输入：覆盖决策信息系统(U,A,D)；

输出：(U,A,D)的约简集B。

Calculate L ∥计算可辨识集簇L

Let B=∅

While (L≠∅)∥取出最大辨识能力的覆盖，消解迭代直至L为空

Let C=max(L).get()

Let B=B∪{C}

Let L=Diss(L,C)

EndWhile∥第一阶段结束，以下开始第二阶段去除冗余覆盖

Let redundant=true

While(redundant==true)

Let redundant=false

Let Q=duplicate(B)∥从B复制一份到Q

While (Q≠∅)

Let C=Q.get()∥从Q中取一个覆盖

Let B′=B-{C}∥根据定义4对B′进行协调性检查

Let consistent=true

For Diin D

Let consistent=false

break

EndIf

EndFor

If (consistent==true)∥B′是协调的

Let B=B′

Let redundant=true

EndIf

EndWhile

EndWhile

Return B

算法1的第一阶段是逐次获取具有最大辨识能力的覆盖并用该覆盖对原可辨识集簇进行消解来获取协调集。具体过程为：首先从可辨识集簇L提取辨识能力最大的覆盖C并加入到协调集变量B中，然后用该覆盖C对L进行一次消解操作得到新的可辨识集簇V，接着再从V提取辨识能力最大的覆盖并进行下一次消解操作，依次类推，直到可辨识集簇为空。最终得到B即为协调集。

算法1的第二阶段是从协调集B中去除冗余覆盖。 主要的策略是反复检查协调集B是否存在某个覆盖去除后仍能保持协调性，直到无法找到为止，最后返回的协调集即为约简集。

从算法1可知该算法可终止，并由定理3和定理4可知，由算法1得到的结果必定包含所有核心覆盖，同时该覆盖集是去除了冗余覆盖的一个约简，结论由定理5给出。

定理5给定决策覆盖信息系统(U,A,D)，采用算法1进行计算，则算法能够结束，且返回的结果B⊆A是(U,A,D)的一个约简覆盖集。

以下给出算法1的时间复杂度和空间复杂度分析，设|U|和|A|分别为论域和覆盖簇的规模大小。

第一阶段：计算可辨识集簇L的时间复杂度为O(|U|2·|A|)，可辨识集簇L的空间复杂度为O(|U|2·|A|)。因为可辨识集簇在消解过程中的规模是逐渐变小的，考虑最坏可能性为覆盖在L中平均分布的情况下，计算辨识能力最大覆盖的平均时间复杂度为O(|U|2·|A|)，空间复杂度为O(|U|2·|A|)。可辨识集簇L的一次消解计算的平均时间复杂度为O(|U|2·|A|，)，平均空间复杂度为O(|U|2·|A|)。算法的循环总数至多为O(|A|)。综合第一阶段时间复杂度为O(|U|2·|A|2)，空间复杂度为O(|U|2·|A|)。

第二阶段：完成去除冗余计算最多去除|A|个，去除一个冗余覆盖最多需要|A|次协调性检查，综合时间复杂度为O(|U|·|A|2)，空间复杂度为O(|U|2·|A|)。两个阶段综合计算复杂度：时间复杂度为O(|U|2·|A|2)，空间复杂度为O(|U|2·|A|)。

由上述计算复杂度的分析可知，采用“提取-消解”迭代逐次得到最大辨识能力的覆盖算法是高效的。

4 相关实验及结果

为了验证算法在实际决策信息系统进行约简的有效性，选取由UCI(university of California Irvine)所提供的5组数据集(如表1所示)进行约简实验，通过对照约简前后的分类准确性来验证算法的有效性，并与相关研究[6]的约简结果进行对比。数据集约简前后的CART (classification and regression tree)、SVM(support vector machines)和3NN(3-nearest neighbor algorithm)分类实验采用Python环境下的scikit-learn库所提供的函数。

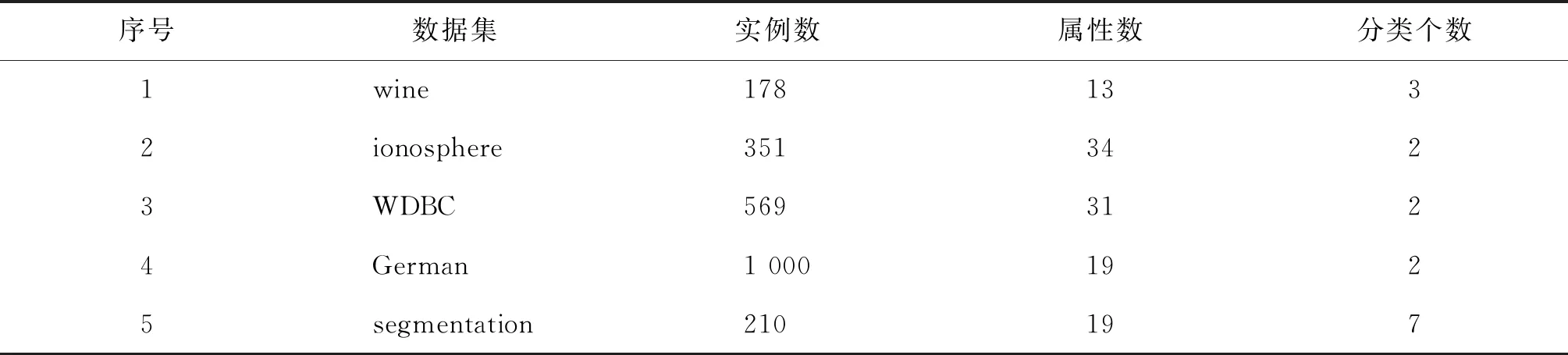
表1 实验使用的UCI数据集Table 1 UCI datasets used in experiment

如表1所示的UCI数据集可视为一个决策信息系统(U,A,F,d)，A是属性集，d是决策属性。F={fa:U→Va}，其中fa表示对象集U在属性a的值域Va上的取值映射，即对象x∈U在属性a∈A上的值可表示为fa(x)。采用文献[14]的方法将决策信息系统(U,A,F,d)转化为覆盖决策信息系统(U,A′,D)，即在任意属性a∈A上构造一个相应的覆盖C∈A′，在决策属性d上构造一个覆盖D。简要叙述如下。

第1步，构造U上对象之间在任意属性a∈A上的邻域关系Ra={(x,y)|x,y∈U, |fa(x)-fa(y)|≤δa}。δa是属性a的邻域半径，它的选取是根据文献[4, 6]给出的方法δa=std(a)·δ，其中：std(a)是属性a的标准差；δ是修正参数，取0.8～1.3可得比较好的约简结果。

第2步，根据每一个属性a的邻域关系Ra构造一个覆盖Ca={Ra(x)|x∈U}。决策覆盖D也按照类似的方法由决策属性d得到，但不同的是还需要考虑具体数据集的决策属性值之间的相容性，如果不相容则决策覆盖D由决策属性d直接得到一个划分。

表2、表3所示的是上述数据集所对应的决策信息系统进行约简实验的结果，其中NRS所在行的数据是基于邻域粗糙集(neighborhood rough set，NRS)的约简结果[6]，CRS(covering rough set)所在行的数据是由本文算法得到的约简结果。

表2给出了来自邻域粗糙集约简和本文算法得到的约简结果。表3给出了数据集未进行约简前的CART、SVM和3NN分类准确率，以及来自邻域粗糙集约简[6]和本文算法的约简属性集(如表3所示)所分别构造的约简数据集进行相应分类实验的准确率。

从表2和表3可知，运用本文算法对数据集进行计算可得到较高的约简率(最大达87.1%)，约简后数据集的分类准确率与约简前相比有一定的提高；同时本算法与邻域粗糙集约简[6]所提供的约简结果相比也有一定的优越性。表明本文基于可辨识集消解策略的覆盖决策信息系统的约简算法能够较好地去除原数据集中的冗余属性。

表2 数据集约简后的属性集Table 2 Selected attributes with different reduction algorithms

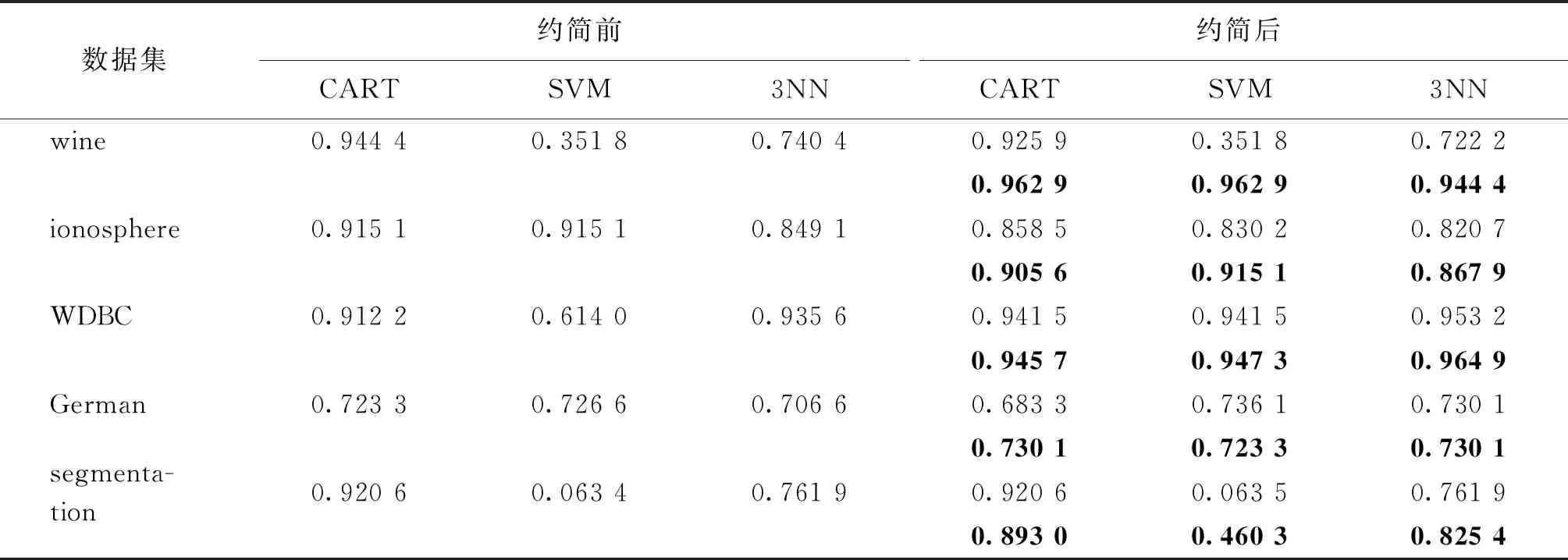
表3 数据集约简前后分类结果对比Table 3 Comparison of the classification accuracies of reduced data

注：约简后的分类结果中加粗数据为本文约简算法的结果，未加粗数据为NRS方法的结果。

5 总结

通过分析覆盖决策系统中的协调覆盖集与对象的可辨识集之间的关系，本文给出了覆盖相对于可辨识集簇的辨识重要度和辨识影响度所构成的覆盖辨识能力，以及覆盖对可辨识集簇进行消解的概念和性质。提出了从覆盖决策系统的可辨识集簇中提取最大辨识能力的覆盖，然后用该覆盖对原可辨识集簇进行消解的逐次迭代计算，直至可辨识集簇完全消解来得到协调覆盖集的算法。

本文算法对可辨识集簇进行逐次地“提取-消解”的迭代计算是很高效的。未来可针对动态信息系统中的增量可辨识集[29]和可压缩的可辨识集[30]运用本算法思想进行高效属性约简的探索工作。