气升式内环流浆态床流动特性实验及数值模拟

薄紫一，夏良志，王浩南，董瑞庭

大连理工大学化工学院化工机械与安全系，辽宁 大连 116024

自21 世纪以来，石油化工产业发展迅速，以乙烯、丙烯为源头的基础原料生产取得长足进步，但部分精细化工产品，如低碳脂肪二胺类产品相对短缺，主要原因在于连续生产装置难以实现工业化[1]。 1,3-丙二胺系列精细化学品是低碳脂肪二胺化合物的重要品种之一，目前制备1,3-丙二胺的工艺主要采用丙烯腈氨化还原法，即以氨化剂与丙烯腈为原料制备3-氨基丙腈，再经加氢催化还原合成 1,3-丙二胺。反应过程需要在一定压力条件下，同时保证气液固三相充分混合，因此对三相反应器有较高的要求。

气升式环流反应器（Air-lift Loop Reactor，ALR）作为由鼓泡床改进而来的新型反应器，是目前应用最广泛的三相反应器之一。ALR 综合了鼓泡床和搅拌釜的优点，与鼓泡床相比，ALR 结构简单、无运动件、混合效果更好、剪切应力更小、传质/传热性能更好、运行功耗更低，且能在较低的表观气速下实现固体颗粒的完全悬浮，更有利于反应物之间的混合和传质过程[2-5]。目前，ALR 广泛应用于费托合成、一步法合成甲醇与二甲醚、汽油脱硫、重油氢化、生物废水处理及发酵工程等[6-10]。

近年来，三相环流反应器的研究逐步成为热点。实验研究方面，黄青山等[11]综述了环流反应器的流动、混合及传递特性。王铁峰等[12]指出气含率和循环液速是环流反应器设计及放大的重要参数。GUO 等[3]讨论了顶部间隙对环流反应器气含率的影响。YANG 等[13]设计了一种带有水力旋流器的内循环浆态床，旨在实现反应器的连续操作。JIN 等[14]使用ERT 技术测定了外循环床上局部气含率和平均气含率，同时讨论了操作条件和固含率对床内气含率的影响。RAZZAK 等[15]同样采用ERT 技术测量环流浆态床升液管的局部相含率，并结合压力传感器确定气、固相含率的轴向和径向分布，采用光纤探头单独测量气含率，利用光纤数据区分升液管内气泡和固体颗粒。BURLUTSKII 等[16]研究了气升式内环流反应器中升、降管截面积比对气含率和循环液速的影响。结果表明，气体流量增加，液体循环速率几乎保持不变；张念等[17]研究了大颗粒催化剂体系下气升式环流浆态床内的流动特性。结果表明，增大固含率，最小循环气速和起始流化速度均显著增大。数值模拟方面，刘敏[18]综述了气升式环流反应器相间作用力模型及简化计算模型，同时分析了气泡分散机理及对湍流作用的影响。LESTINSKY 等[19]基于COMSOL 软件研究了导流筒直径的变化对流动特性的影响，确定了气泡直径和气泡阻力系数的适用条件。采用瞬态模拟模型，分析了0～60 s 反应器内部的流动过程，忽略了气泡的破裂和聚并。XU 等[20]根据各相物性及研究角度的不同，将浆态床相间作用力封闭模型划分为4 类。杜峰等[21]采用双流体模型研究了导流筒直径对环流反应器流动的影响及放大。YUAN等[22-23]基于CFD研究了两相体系下环流浆态床的流动及传质特性；BURLUTSKII 等[15]基于双流体模型建立了气升式外环流反应器的三维数学模型，相间作用力考虑了气动阻力、剪切升力和附加质量力，模型另考虑了湍流扩散效应和气泡的分裂-聚并过程。LAW 等[24]模拟了外环流反应器内气液两相流动过程，研究了不同类型降液管结构对流动的影响。徐斌等[25]采用三欧拉模型描述各相流动，同时采用改进的相间曳力模型，描述二维体系下内环流生物反应器的流动过程，讨论了降液管内的最大及时均液体循环速度变化规律。

本工作设计了一种带有固液分离装置的气升式内环流浆态床反应器。从实验和数值模拟两个方面，对气含率及液相循环速度两个重要参数开展研究，讨论了压力及固含率对流动特性的影响。基于Fluent软件，建立气升式内环流浆态床的数值模型。作为可实现1,3-丙二胺系列精细化工产品连续化制备的载体，气升式内环流浆态床内部多相流动和传递行为十分复杂、工业放大设计难度大。因此，针对反应器流动特性的研究为后续结构设计和传热、传质的优化具有重要意义。

1 实验部分

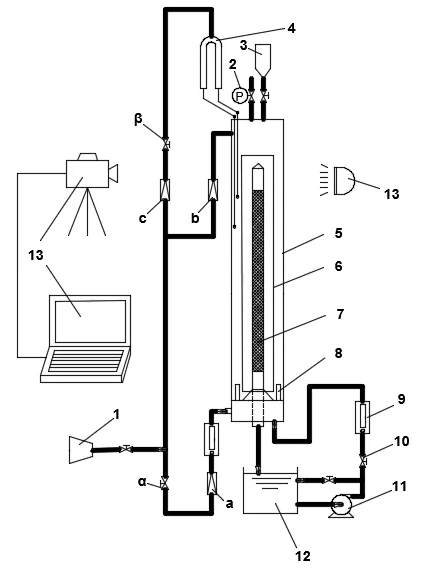
图1 实验装置 Fig.1 Experimental setup

1.1 实验装置

实验装置如图1 所示，平台主要由气升式内环流浆态床、空气供给系统、液相循环系统、液固分离系统、高速摄像采集系统及压差测量系统6 部分组成。浆态床筒体材料为玻璃，通过4 根不锈钢柱和2 个法兰实现密封，上法兰盘装有背压阀、填料器和倒置U型管压差计。相比于电导探针和光纤探头，倒置U 型管压差计更适用于高固含率、透光性能差和电导率低的气液固三相体系压差测量。浆态床高1 000 mm，内径100 mm，导流筒高800 mm；导流筒内安置外径32 mm，高810 mm，滤网目数为400 的液固分离器。气体分布器由6 个外径8 mm，高20 mm 的气泡器组成，气泡器在周向上呈环形阵列均布。以空气-水-白炭黑为实验体系，各相的物性参数如表1 所示。

采用Photron 公司的FASTCAM SA4 型高速摄像机，最高分辨率为1 024×1 024 像素，最短曝光时间1 µs，最大拍摄速度为5×105fps。摄像机及光源布置如图2 所示，实验采用AF 50mm f/1.4D 镜头近距拍摄，综合考虑采样时长与气泡辨识度，确定最佳采样频率为1 000 fps。考虑到设备外壁为玻璃圆柱，为减小光线折射对参数采集的影响，因此采样区域所在横截面的圆心角2α应小于60°。

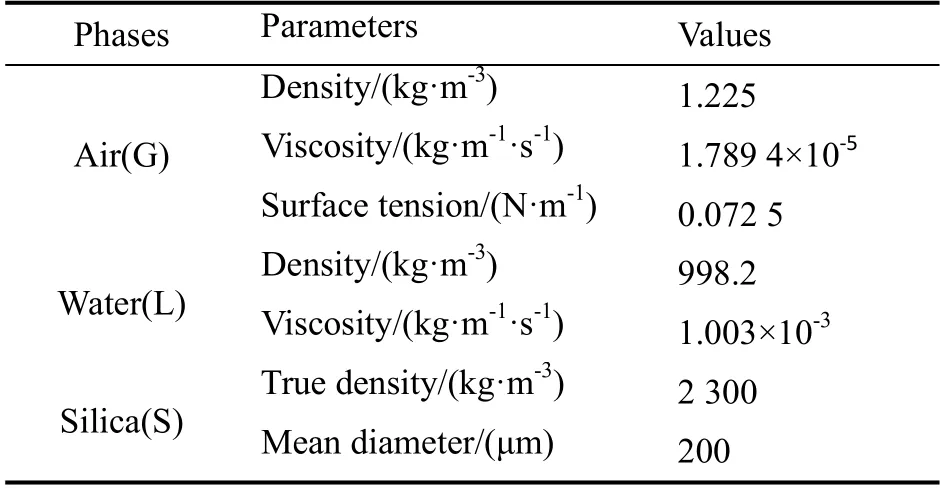
表1 各相物性参数 Table 1 Property parameters of each phase

图2 高速摄像机及光源布置 Fig.2 Shooting angle and light source arrangement

1.2 气含率

气含率测量区域为轴向高度在500～800 mm 的升液区，因为此处流场已发展完全，如气泡形状、分布及上升速度等特性参数的波动较小。实验测定该区域内任意两点对应的U 型管内液面高度差 （ΔH，m），则流场内两点间的压差（ΔP，Pa）与各相含率关系如式（1）所示：

式中：ρ为密度，kg/m3；ε为相含率；g为重力加速度，m/s2；下标g，l 和s 分别代表气相、液相和固相。气液固三相间满足归一化方程，如式（2）所示：

由于固相颗粒密度及粒径较小，可在较低的表观气速条件下实现均匀分布，因此，固含率可通过式（3）求解，再由式（1）和（2）求解两点间的平均气含率。

式中：Ws为固相总质量；V为反应器连续相所占容积。

实验装置在稳定运行时液相产率为5 kg/h。浆相在床内循环流动时，部分固相会附着在滤网表面形成滤饼。循环的浆相不断冲刷滤饼表面，成长到一定程度的滤饼会脱落，继续参与下一循环。周期性变化的过滤阻力波动幅度小，频率低，因此，忽略周期过滤阻力波动对床内整体流动特性影响。

实验测定的气含率随压力变化关系实验如图3（a）所示，固含率均为0.10。由图可知，不同压力条件下，气含率随表观气速近似呈线性增加。低表观气速下，各压力工况间气含率相差不大，最大偏差产生于表观气速0.028 m/s。图4 为固含率0.10、压力0.0～0.2 MPa 下气泡平均直径随表观气速的变化规律。随表观气速增大，0.2 MPa 气泡的平均直径的增幅小于常压工况，表观气速达到0.028 m/s时，0.2 MPa 和常压对应的气泡平均直径分别为4.09 和4.31 mm。由实际流场拍摄图5（a）和（b）看出，相比带压操作，常压下气泡平均直径更大，多呈椭球状。椭球状气泡上升时受到的流动阻力较比同体积的球状气泡更大，且轨迹多为螺旋式上升，气泡平均上升速度更低，因此单位体积内气泡个 数减少，气含率降低。操作压力改变了气泡形状，进而影响气泡的上升速度，这是气含率发生变化的主要因素。表观气速较低时，不同压力下气泡平均直径相差较小，且形状区别不大，实际观测中并未观测到大量螺旋式上升气泡，因此气含率几乎没有差别。

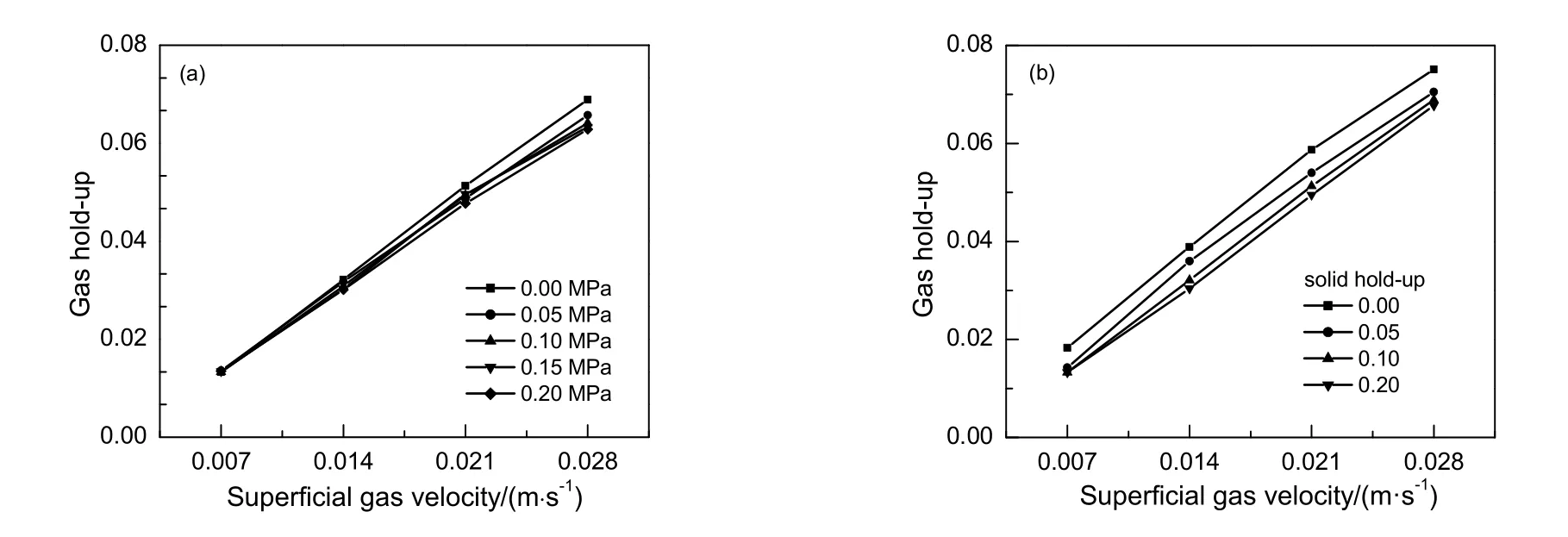
图3 不同压力和固含率工况下气含率随表观气速的变化规律 Fig.3 Changes of gas hold-up with superficial gas velocity under different pressure and solid hold-up

气含率随固含率变化关系如图3（b）所示，操作压力均为常压。由图可知，不同固含率工况下气含率随表观气速的增高均增大，在同一压力及表观气速下，高固含率工况具有较低的气含率。主要原因在于气相和浆相密度差增大，推动气泡上升的浮力增大。另一方面，固相的引入增大了浆相的黏度，因此表面张力增大，液面有收缩的趋势，流场内部气泡球形度增大。由流动阻力与迎风面积的关系可知，球形度更高的气泡所受阻力更小。二者共同作用下，高固含率体系内气泡平均上升速度增大，单位体积内气泡数量减少，同表观气速下气含率更低。

图4 压力0.0～0.2 MPa 下气泡平均直径随表观气速的变化 Fig.4 Changes of average bubble diameter with superficial gas velocity under 0.0-0.2 MPa pressure

图5 常压（a）和0.2 MPa（b）下的气泡特性 Fig.5 Bubble characteristic of (a) normal pressure and (b) 0.2 MPa solid hold-up 0.1; superficial gas velocity 0.028 m/s

1.3 流型转变气速

流型转变气速同样是环流浆态床的重要参数之一。随着升液管中表观气速的不断提升，环流浆态床共经历了3 个流型即均匀鼓泡流、过渡流和非均匀鼓泡流，或称流型I、流型II 和流型III。流型II属于一个相对稳定状态，在表观气速的轻微波动下，流型II 会向流型I 或III 转变，本装置降液管中较难观测到清晰而稳定的气泡悬浮区。因此定义流型转变气速为脱离流型I 状态前的最大表观气速与维持流型III 状态的最小表观气速之和的算术平均值。

流型转变气速随压力和固含率变化规律如图6 所示，由于固含率达到0.20 时难以直接观测到降液管内气泡运动状态，因此实验只在固含率0.00，0.05 和0.10 三种工况下进行。由图可知，压力相同时，固含率较高的体系具有更高的流型转变气速。达到流型III 需要满足降液区中气泡滑移速度小于浆相宏观运动速度，可以从两方面对这一现象进行解释：1）相同操作条件下，高固含率体系中 气-浆相密度差更大，气泡所受浮力增大。另外，固相引入会使气泡球形度更高，气泡所受阻力减小，二者共同抑制气泡流入降液区，即抑制流型向III 转变；2）引入固相后，浆相的黏度上升，循环阻力增大，因此降液管中浆相宏观运动速度下降，同样抑制流型向III 转变。另外，由图可知，固含率相同，压力对流型转变气速的影响较小。这是因为在本实验操作范围内，因压力变化产生的气泡特性差异对流型转变气速作用效果并不显著，通过观察法确定流型转变气速的精确度存在一定的局限性，难以捕捉小尺度特性变化对宏观流动的影响。

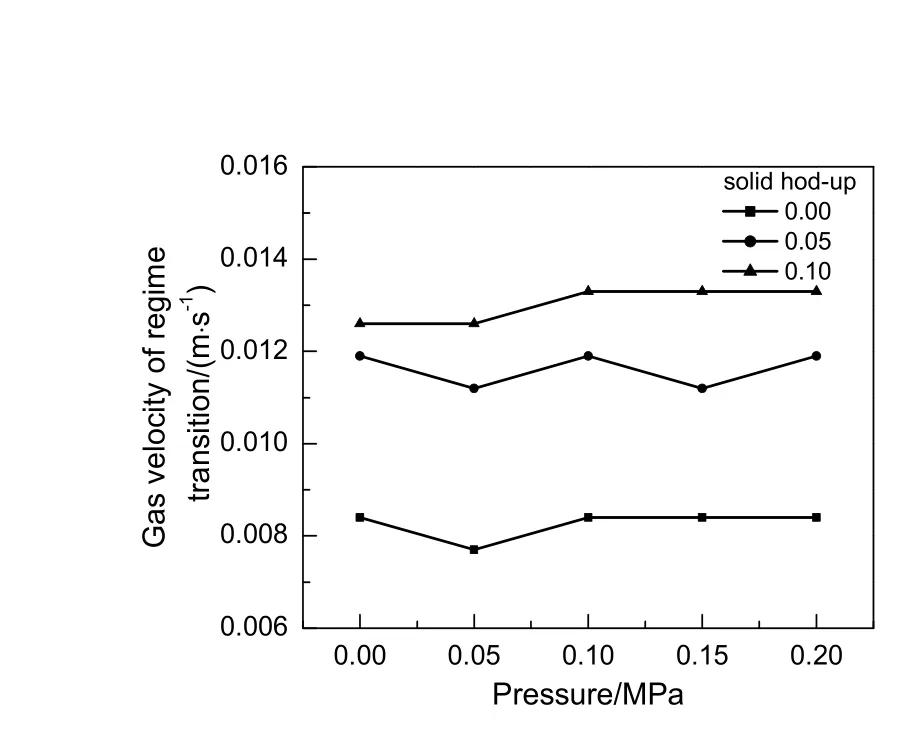
图6 不同压力及固含率下流型转变气速 Fig.6 Gas velocity of regime transition under different pressure and solid hold-up conditions

图7 物理模型 Fig.7 Physical model

2 气升式环流浆态床数值模型建立

2.1 物理模型及网格划分

本工作建立的物理模型基于Fluent 平台，模型尺寸与实际设备尺寸之比为1:1。实验装置结构的分布为轴对称式，为了减小计算量，采用周期性边界条件建立三维内环流浆态床物理模型，如图7 所示。采用Gambit 对反应器网格进行划分，网格数目约1.7×105个，在模型计算中开启自适应网格，以提高收敛速度及准确程度。

2.2 数学模型

（1）连续性方程

采用三欧拉模型模拟气液固三相流动。各相所占据的空间体积通过各自的体积分数描述，其中三相体积分数εg，ε1和εs之和为1，如式（4）～（6）所示。

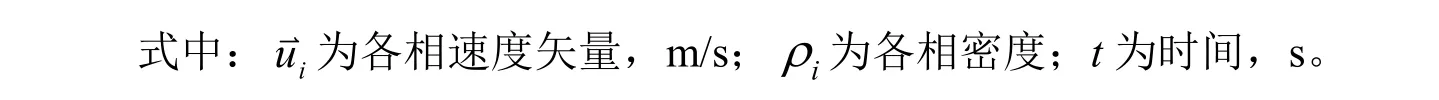
（2）动量方程

式（7）和（8）分别为气、液相的动量守恒方程，两等式右侧各项分别代表应力、压力梯度、重力和相间动量交换作用力。式（9）为固相的动量守恒方程，等式右侧分别代表固相应力、固相压力梯度、因颗粒碰撞产生的附加固相压力、固相重力和相间动量交换作用力。

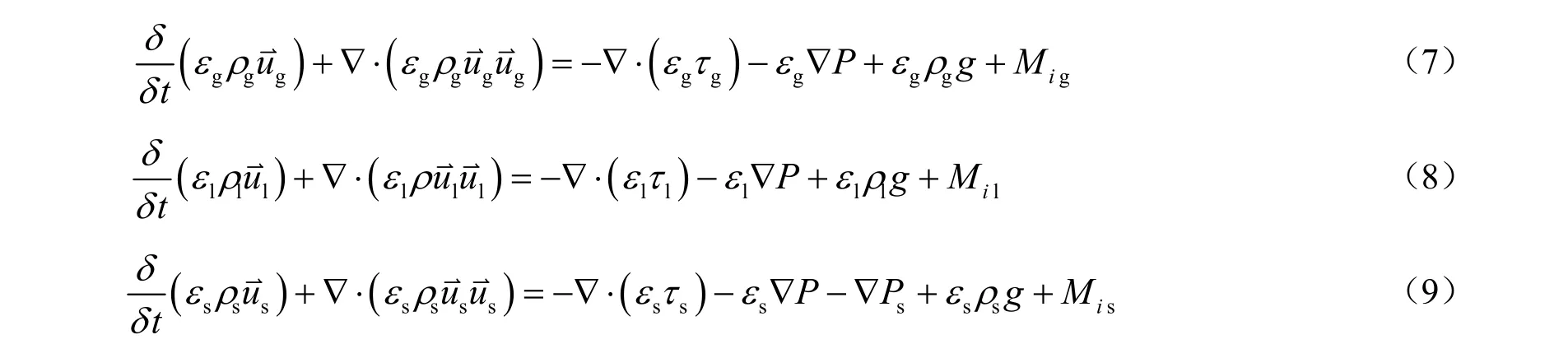
式中：Mi为各相相间作用力，N/m3；τi为流体微元中各相所受应力张量，Pa。

动量守恒方程中应力表达式如式（10）～（12）所示，有效黏度公式如式（13）～（15）所示。

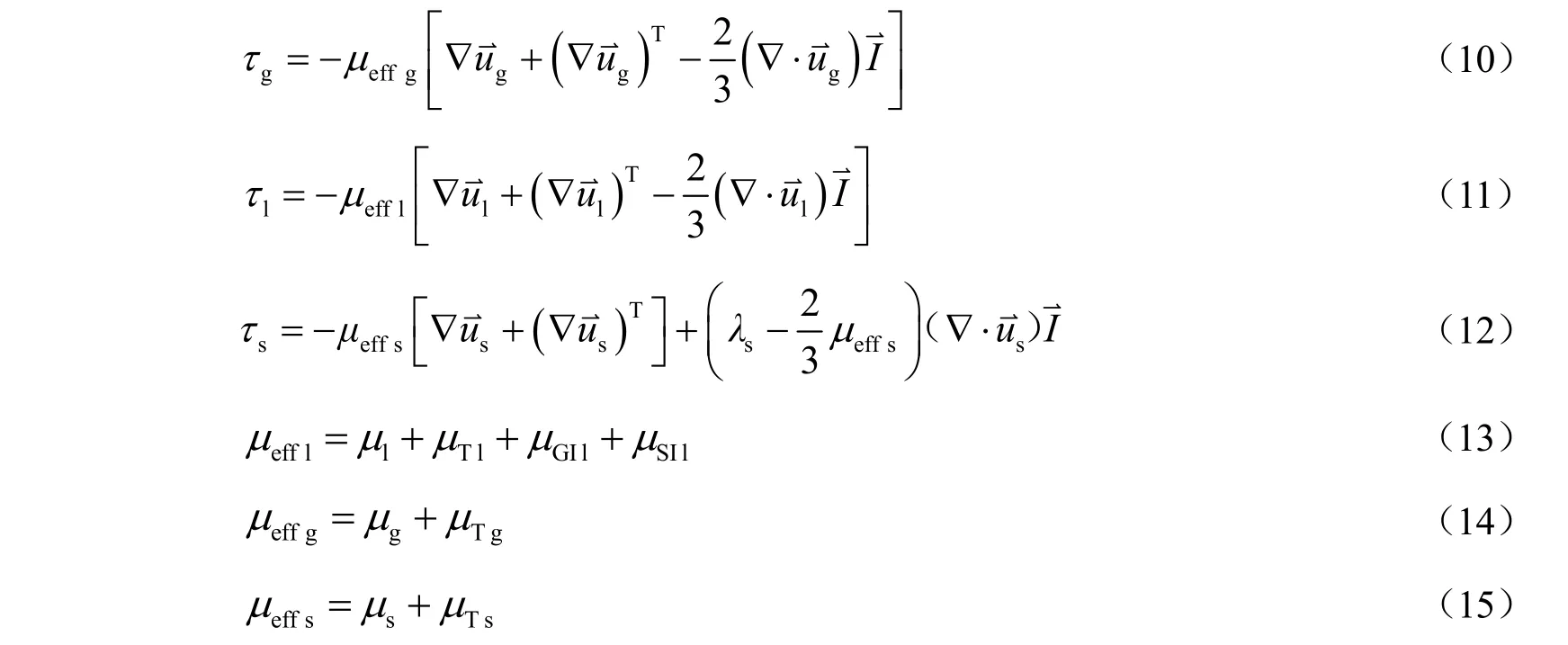
式中：μeffi为各相有效黏度，Pa·s；λs为颗粒剪切黏度，Pa·s；⇀I为单位张量；T 为转置符号。

液相有效黏度由4 部分构成，分别为液相黏度μ1，由涡黏度引起的剪切或液相湍流黏度（μTl），气相和固相引起的湍动黏度（分别为μGIl和μSIl）。式（10）～（12）中各项表达式如式（16）～（21）所示：

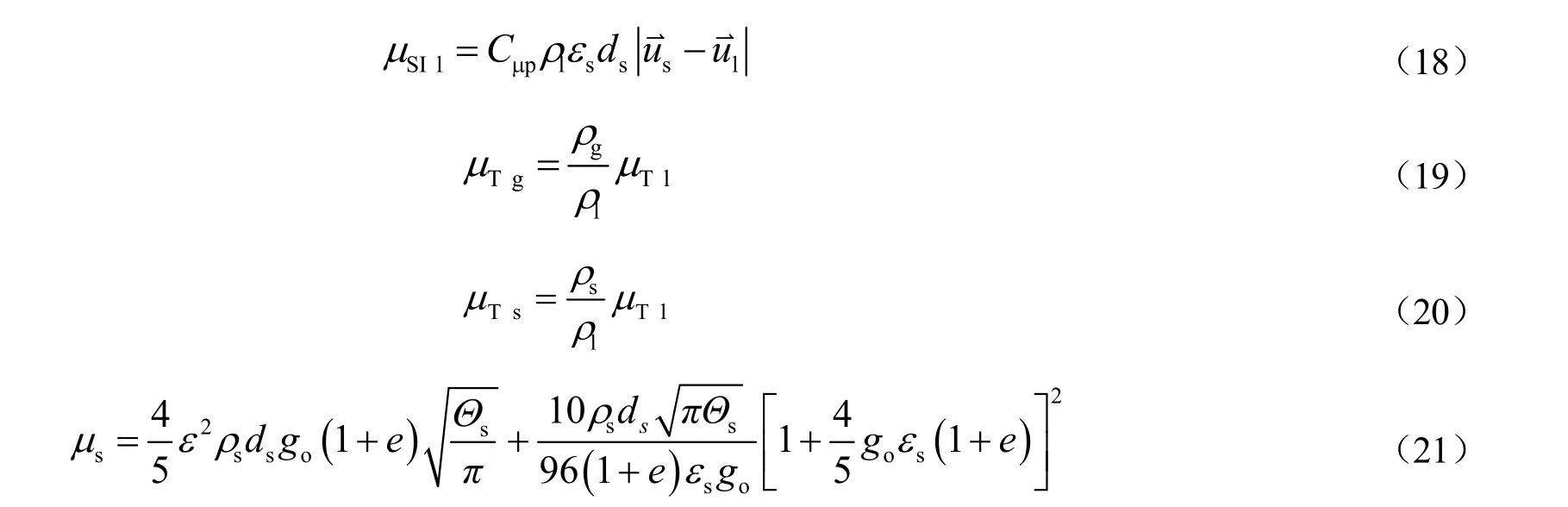
式（10）为固相的动量守恒方程，采用颗粒动力学模型（Kinetic Theory of Grannular Flow，KTGF）对颗粒相应张量（τs，N/m2）和附加固相压力（Ps，Pa）进行封闭，如等式（22）～（25）所示。模型中考虑了颗粒间的碰撞作用。

（3）湍动模型

根据文献[26]可知，RNG kε湍流模型能够更好地描述鼓泡床中的湍流运动。RNG 模型对N-S方程进行重整，以获得对小尺寸运动的影响。相比于标准k-ε湍流模型只采用一个湍动尺度计算涡黏度，RNGk-ε湍流模型通过变化生成项考虑各个尺度运动情况，其表达式如式（26）和（27）所示。

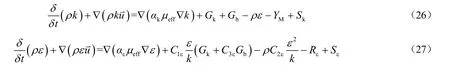
RNGk-ε湍流模型中，σk表示为有效施密特数σeff，其计算公式如式（29）所示，1/σ0≈1.0。

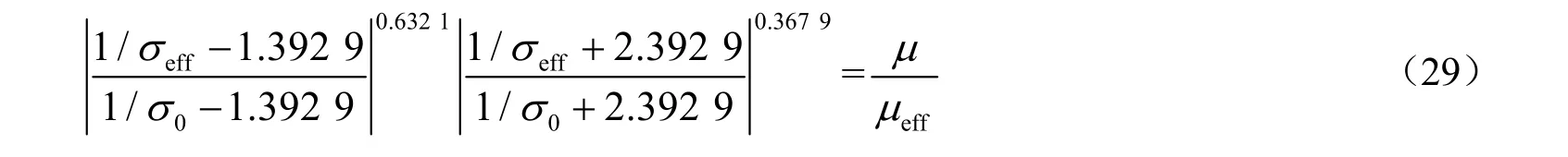
（4）相间作用力

环流浆态床中相间作用力主要包括：曳力、升力、附加质量力、湍动扩散力、壁面润滑力和Basset力[27]。其中，曳力起到决定性作用，另外，升力在气液分离区及浆态床底部这样的大速度梯度变化区起到作用不可忽视[18]，因此相间作用力同时考虑曳力和升力，忽略其它作用力。气液相间曳力及升力选择低雷诺数下广泛采用的Tomiyama 模型，液固间升力作用采用基于漩涡涡脱落的非黏性叠加理论与实验拟合的Moraga 模型[28]，忽略气固相间的曳力作用。曳力及升力模型设置如表2 所示。

表2 相间作用模型设置 Table 2 Interphase interaction model settings

2.3 边界条件设定

采用三欧拉模型进行气液固三相流的非稳态模拟计算。RNG kε湍动模型设置为Dispersed，动量方程采用二阶迎风格式，时间和空间导数采用一阶迎风格式求解，压力与速度耦合采用phase-coupled SIMPLE 法，壁面条件为无滑移。模型采用单一固定的气泡直径。添加不同轴向高度的升、降液区气含率监测，待流场达到伪稳定状态后，进行时间平均采样。模型初始化设置中，固相以均匀分布形式Patch 在主流域以缩短稳定时长。计算中模型约在20 s 达到伪稳定状态，总时长达到50 s后停止计算。模型其它基本参数设置如表3 所示。

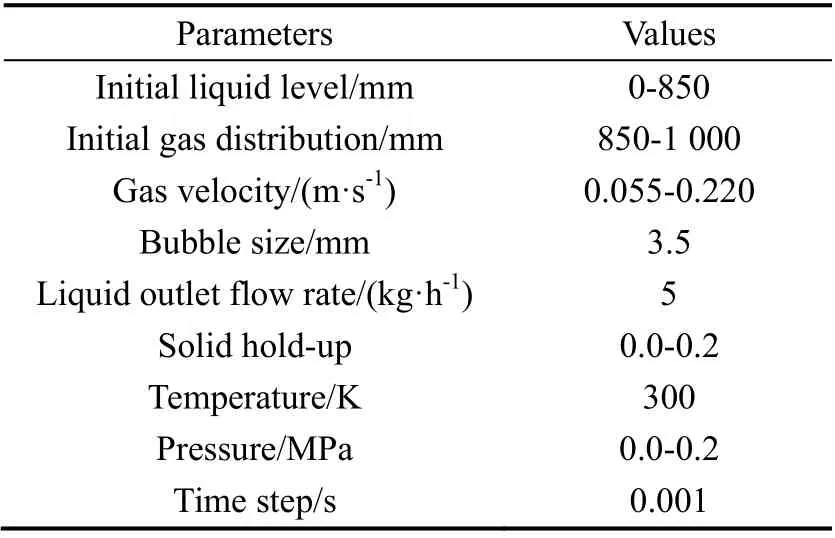
表3 模型基础参数设置 Table 3 Model base parameters settings

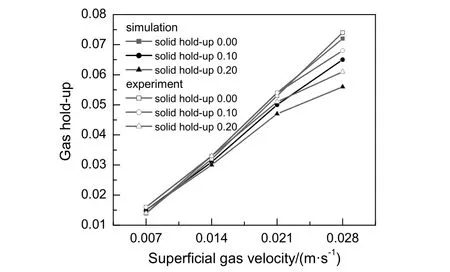
图8 气含率模拟计算与实验结果对照 Fig.8 Comparison of gas hold-up between simulation and experimental results

2.4 模型验证

气含率模拟计算结果与实验数据对照如图8 所示，由图可知，模拟结果与实验测量值吻合情况较好，固含率0.20、表观气速为0.028 m/s 的工况条件下，存在8.9%的最大相对偏差。另外，固含率0.10和0.20 工况下的实验测量值一般高于模拟结果，除模型方面的原因外，倒置U 型管差压计测气含率时同样会产生一定误差，这是由于管内浆相几近停滞，部分固相发生沉降，管内近液面处的浆相平均 密度减小，液柱间的差值增大，气含率实验结果偏大。另从流型转变气速进行模型验证，如表4 所示。模拟计算的流型转变气速，定义为降液区近液面处恰好产生y轴负方向气相矢量与降液区中气相恰好产生y轴正方向气相矢量，两时刻下对应的表观气速的算术平均值。在固含率为0.00～0.10 条件下，模拟计算的流型转变气速与实验数据存在5.0%的最大偏差，吻合情况较好。

表4 流型转变气速模拟与实验结果偏差 Table 4 Deviation of gas velocity of regime transition between simulation and experimental results

2.5 液相循环速度

液相循环速度随压力变化的模拟结果如图9（a）所示，模拟工况固含率为0.10。这里的液相循环速率定义为降液管中浆相的轴向宏观运动速度。由图可知，表观气速在0.007～0.028 m/s 范围内，不同压力下的液相循环速度均有增加，但相同压力下差别不大。因此在同一固含率下，液相循环速度受压力变化影响较小。

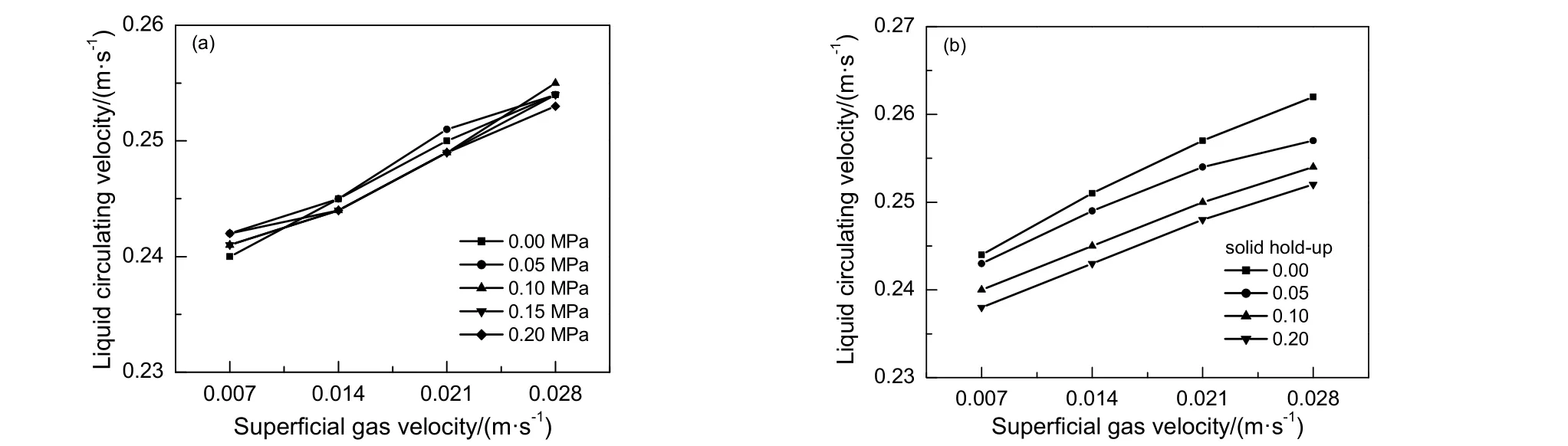
图9 不同压力和固含率工况下循环液速随表观气速变化 Fig.9 Changes of liquid circulating velocity with superficial gas velocity under different pressure and solid hold-up conditions

液相循环速度随固相浓度变化模拟结果如图9（b）所示，模拟工况为常压。表观气速达到0.028 m/s时，固含率0.20 工况下液相循环速度为0.252 m/s，固含率0.05 对应的值更高，但依然小于气液两相体系下的循环速度。从循环动力角度解释，增加固相后，连续相的表观黏度提升，因此上升管气含率减小，进而升降液区的压差减小，推动力减弱，液体循环速度下降。从循环阻力的角度来解释，浆相的平均密度及表观黏度上升，环流阻力上升，同样会造成循环速度下降。

3 结 论

本工作设计了一种可实现连续操作的气升式内环流浆态床反应器，采用三欧拉法及RNG kε湍流模型建立其数值模型。表观气速0.007～0.028 m/s 的范围内，实验及数值模拟分析得到主要结论如下：

a）压力0.0～0.2 MPa 范围内，压力对气含率和液相循环速度的影响较小。不同压力下气含率存在一定的差异，主要原因在于压力改变了气泡形状，导致气泡平均上升速度不同，造成气含率的不同；

b）固含率0.00～0.20 范围内，固含率增大会降低相同条件下气含率及液相循环速率，增大流型转变气速；

c）采用倒置型U 型管压差计测量气含率得到的结果一般高于模拟计算结果，主要因为测量时U型管内部固相发生沉降，浆相密度减小，测得实际气含率数值偏高。倒置型U 型管对高固含率体系中气含率测量存在一定局限性。