振幅对振荡流结晶器传热效果影响的数值研究

刘子矜，张春桃

武汉科技大学化学与化工学院, 湖北 武汉 430081

振荡流是指按照一定规律如正（余）弦周期变化流动的流体，振荡换热就是利用振荡流来代替稳态流，获得换热效果的新技术[1-3]，其对传热及流动特性的研究[4-8]也成为近几年的研究焦点，CHANG 等[9]利用数值法研究了水平挡板对平行垂直明渠中振荡流动体系传热特性的影响，发现当雷诺系数（Re）增加时，振荡流动逐渐主导了通道中的速度振荡，传热效果随Re的增加而增加，振荡流动结合带挡板的通道具有更好的传热效果。SUKSANGPANOMRUNG 等[10]利用数值模拟研究了振荡流动对矩形钝板上二维流动和对流换热的影响，结果表明在低雷诺数状态下，振荡流的振幅和频率的改变将破坏流体稳态流动，并随着涡流的形成而迫使流体流态变得不稳定，这些漩涡在能量传输中起重要作用。OLAYIWOLA 等[11]通过实验研究了矩形翅片管内流动脉动对横流输运和对流换热强化的影响，研究发现，随着振幅的增大，振荡流动对换热系数的强化作用越来越明显。HOFMANN 等[12]研究了振荡对流动结构以及传热效果的影响，发现对流换热受流体周期波动的影响。

振荡流结晶器（Oscillatory Baffled Crystallizer，OBC）是一种新型连续型化工工程生产设备，由于其具有特殊的周期性速度边界及挡板式结构，流体湍动程度提高，因此研究振荡流结晶器的传热效果对优化振荡流结晶器性能有重要意义。

1 振荡流结晶器的物理模型及数学模型

1.1 物理模型

传统的振荡流结晶器为套管式，通过在外部套管通入冷凝水来达到内外换热的目的，壳程冷凝水流量较大时，冷凝水进出口温度变化较小，为简化计算去掉振荡流结晶器的壳程套管，内流体的外边界选取固定壁面温度的操作，使之等效于套管换热的效果。图1 为振荡流结晶器几何结构示意图。管壁材质采用3.3 硼硅酸盐玻璃，其物理化学性质为密度为2 230 kg/m3，比热为900 J/(kg·K)，以及热导率为1.2 W/(m·K)。

图1 振荡流结晶器几何结构示意图 Fig.1 Structure diagram and grids of oscillatory baffled crystallizer

1.2 数学模型

振荡流结晶器内的振荡流体的流动由以下3 个无因次参数进行表征：

振荡雷诺数：

净流雷诺数：

斯特劳哈尔准数：

其中：f代表频率，Hz；x代表振幅，m；D代表管道内径，m；ρ代表流体密度，kg/m3；µ代表流体黏度，Pa·s；u代表平均净流速度，m/s。振荡雷诺数Re0反映了振荡流反应器内流体的混合强度；斯特劳哈尔准数St代表管径与振荡幅值的比值，表征漩涡的传播程度。

根据压缩黏性流体非稳态控制方程[13]，描述可压缩振荡流动和传热的控制方程如下：

连续性方程：

动量方程：

能量方程：

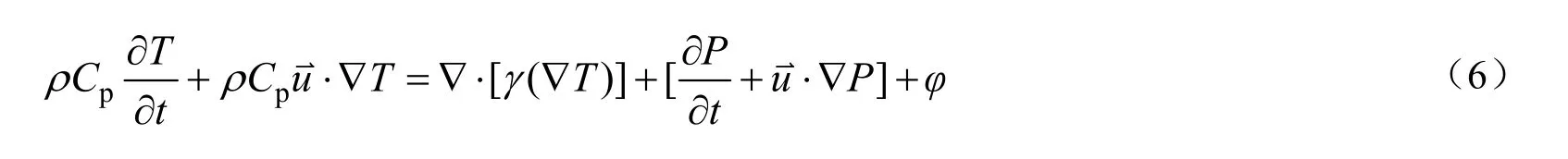
其中：t代表时间，s；P代表压力，Pa；T代表温度，K；Cp代表定压比热容，J/(kg·K)；γ代表热导率，W/(m·K)；u⇀代表速度矢量，m/s；φ代表由黏度引起的能量耗散，W/m3。

振荡流结晶器内流体的混合受到反应器的结构、振荡频率和振幅的控制，而几乎不受净流速的控制[14]，所以探究同一几何结构下的振荡流结晶器的传热效果，振荡幅度以及振荡频率便是最重要的两个参数。本工作通过数值模拟的方法探究不同振幅对振荡流结晶器传热效果的影响。

数值模拟计算采用三维双精度求解器，计算模型选择SSTk-ω湍流模型。压力控制方程选择PREST0!离散方式进行压力插值，压力和速度耦合选择PISO 算法，时间步长设为1/8 周期。模型采用周期性速度进口以及压力出口，周期性速度边界表达式见公式（7），采用水作为数值模拟计算的流体介质，进口温度为353 K，恒定壁温设置为293 K，壁面厚度1 mm。探究5 种不同振幅下振荡流结晶器的传热效果，边界条件的设置见表1。

表1 边界条件设置 Table 1 Setting of boundary conditions

1.3 模型验证

1.3.1 网格独立性验证

瞬态计算对网格的质量要求较高，既要保证模拟的准确性不受网格尺寸的影响，又要尽可能的降低网格数量节省计算资源，因此需要先进行网格独立性验证。采用Meshing 18.0 对流体域进行六面体网格的划分，并采用四套网格尺寸，网格数量分别为239 774，123 552，27 447 和18 887，图2 为网格数为123 552 时的流体域网格划分示意图。

图2 振荡流结晶器内流体网格划分示意图 Fig.2 The grids of oscillatory baffled crystallizer

不同网格尺寸对振荡流结晶器壁面平均热流密度在第8 周期内随时间的影响分别如图3 所示。振荡流结晶器壁面平均热流密度随着网格数量的增加而增加，但当网格数量由123 552 增加至239 774时，两条壁面平均热流密度曲线较为接近（相差1.82%），而网格数量为27 447 和18 887 的壁面平均热流密度曲线较网格数量为239 774 的壁面热流密度曲线相差较大，分别相差分别为4.63%和4.87%。综合考虑计算精度和计算资源，本研究数值模拟均采用网格数量为123 552。

1.3.2 流动变化规律稳定性验证

对于振荡流结晶器特殊的周期性速度边界条件，理论上在一个周期内流体介质的传热与流动规律应与前后周期内的变化规律相似，然而数值模拟研究中发现，计算所得到的流动变化规律常常需要一定时间才会趋于稳定，在此之前计算模拟结果受初值影响较大；而在此之后振荡流动在不同振荡周期内变化规律趋于相同，更能准确反应出振荡流结晶器管程内流体的流动与换热特性。本研究通过检测第1 至第8 周期的壁面平均热流密度以及Nu数确定流动变化规律来确定达到稳定所需时间。

图4 为不同周期下壁面热流密度随相位点的变化图，第1 周期内壁面热流密度曲线与第2 至第8 周期的热流密度曲线形状差异极大，第2 周期壁面热流密度曲线较后面6 个周期有较小的差异，而从第3 周期开始，壁面热流密度曲线基本趋于平行。图5 为不同周期Nu数随时间的变化图，从第3 周期开始，Nu数的变化规律趋于稳定。第4 周期与第3周期的壁面热流密度平均相差1.80%，Nu数平均相差仅有0.78%。因此，综合考虑换热效应和计算计时消耗，将第3 周期后的流动视为流动变化规律进入稳定后的状态。

图3 采用不同网格尺寸计算得到的壁面热流密度在第8 周期内随时间的变化图 Fig.3 Variation of wall heat flow density calculated with different grid sizes over time in the 8th cycle

图4 不同周期下壁面热流密度随相位点的变化图 Fig.4 Variation of wall heat flux with phase point at different periods

图5 不同周期Nu 数随时间的变化图 Fig.5 Change of Nu number with time in different periods

2 振荡流结晶器流动特性研究

图6 为具有周期性速度边界的振荡流结晶器中心腔室在一个周期内的速度矢量图。通过观察可以得到流体的运动规律，上半周期，流体向右运动，在腔室左侧挡板和管壁之间先出现对称的漩涡，与此同时流体在右侧流体中心处也形成一对对称的漩涡，随着流体的流动以及不断有回流液体涌入腔室，漩涡逐渐变大，到(3/8)T时腔室右侧中心处漩涡逐渐扩散到与管壁接触，与腔室左侧漩涡形成对称，腔室内四个漩涡填充满整个腔室，随后腔室右侧漩涡减小，腔室左侧漩涡向腔室中心扩散，流体在(1/2)T时与(1/8)T时的流动方向相反但流态基本一致；下半周期，流体的运动规律与上半周期一致，而流动方向与上半周期相反。

图6 一个振荡周期内流体的速度矢量图 Fig.6 Velocity vector of fluid in one oscillation cycle

图7 为不同振幅下流体的速度矢量图，选取同一周期内的(1/8)T，(3/8)T和(5/8)T三个相位点作为参考点，通过观察可以发现，当x为30 和50 mm 情况下，随着振幅的增加，主体流速增大，同一个相位点下的漩涡增大，增强了流体的湍动，但在x为50 mm 下，腔室内漩涡不明显。

图7 不同振幅下流体的速度矢量图 Fig.7 Velocity vector of fluid at different amplitudes

3 振荡流结晶器传热特性研究

图8 为不同振幅下第1，4，8 和11 腔室中心点温度随时间的变化图，在不同振幅下，观测点的温度随时间的变化趋势一致，在每个周期内，观测点的温度先降低后上升呈现波浪状，而上升后的温度又低于周期开始时的流体温度。由图8 可知，振荡流结晶器振幅小的温度曲线平均温度大于振幅大的温度曲线平均温度，且振荡流结晶器振幅越大，降温速度越快，观测点的温度曲线振幅也越大，当温度降低到与壁面温度和出口温度相同时，观测点的温度曲线周期变化，周期间相对稳定，当x为100，50，30 和20 mm 时，观测点的温度分别大约在10，12，15 和25 s 时趋于稳定，而当x为10 mm 时，观测点的温度在25 s 时还未达到稳定。

图8 不同振幅下腔室中心点温度随时间的变化图 Fig.8 Change of temperature of cell center point with time at different amplitudes (a) 1st cell(b) 4th cell(c) 8th cell (d) 11th cell

3.1 振荡流结晶器轴向温度分布规律

图9 为振幅为20 和50 mm 下流体的温度云图。

图9 不同振幅下流体的温度云图 Fig.9 Temperature distribution of fluids at different amplitudes

由图8 可知，在相同振幅的情况下，随着流动时间的增长，流体的温度沿管长方向逐渐降低，第11 腔室的温度最先降低，而在不同振幅的情况下，对比同一时间下的温度云图可以看出，振幅越大，管内流体轴向温度降低的越快，管内流体与壁面之间的传热效果越好，管内流体的平均温度就越低，其原因可根据图7 得到的结论进行分析，振幅增加，管内生成的漩涡尺度增大，流体的返混程度加剧，流体的湍动增加，降低了边界层的厚度，使流体与恒温壁面之间的传热效果提高。

3.2 振荡流结晶器径向温度分布规律

在第1，4，8 和11 腔室中心截面选取3 个参考点来观测径向温度的变化规律，其中point 1 为 第i腔室中心截面的中点，point 2 为第i腔室中心截面半径中点，point 3 为第i腔室中心截面近壁点。图10 为3 个参考点温度随时间的变化图，可以发现振荡流结晶器的径向温度分布规律，近壁点温度最低，截面中心点温度最高，且近壁点的温度远小于管内点的温度。

图10 参考点温度随时间的变化图 Fig10 Change of temperature of reference point with time

图11 第11 腔室中心点径向速度随时间变化图 Fig.11 Change of radial velocity with time at the center point of the 11th cell

图12 第11 腔室中心点温度随时间变化图 Fig.12 Change of temperature with time at the 11th cell’s center point

通过对比两者之间的关系可以发现，当径向速度为流向腔室中心方向时，观测点的温度升高；当径向速度为由腔室中心流向管壁方向时，观测点的温度降低，因此，在振荡流动时，流体的温度受径向速度的影响剧烈，这也是振荡流结晶器轴向温度呈波浪形下降趋势的主要原因。

4 振荡流结晶器流动阻力特性研究

流体流经振荡流结晶器时，由于其周期性的进口速度边界条件以及特殊的挡板式腔室结构，往往会比传统进口速度为常数的圆形直管存在更大压力损失，即振荡流反应器的进出口压差。图13 为第8 周期内不同振幅下进出口压差随时间的变化图，可以看出，无论振幅的大小，振荡流结晶器的进出口压差曲线趋势基本一致，在一个周期内均存在正压差及负压差，负压差的形成是因为流体回流导致，振荡流结晶器原本的出口相当于流体回流时的速度进口，沿管程负方向存在压差。比较不同振幅下的压差曲线可以看出，大振幅的压差的绝对值始终大于小振幅的压差绝对值，通过观察第8 周期内不同振幅下振荡流结晶器内流体平均速度随时间的变化图（图14）可知，较大的振幅使得流体在振荡流结晶器中存在较大的平均流速，而流体流速又是影响压力损失的一个因素，由伯努利方程可知在流体介质及管道形状一致的情况下，流体流速越大，沿管程的压力损失越大。

图13 不同振幅下进出口压差随时间的变化图 Fig.13 Change of pressure difference with time under different amplitudes

图14 不同振幅下振荡流结晶器内流体平均速度随时间的变化图Fig.14 Changes in the average velocity of a fluid over time under different amplitudes

5 振荡流结晶器传热特性综合评价

图15 不同振幅下Nu 数随时间的变化图 Fig.15 Changes of Nu number with time under different amplitudes

Nu数是一个常见的评价传热效果的无量纲指数，Nu数越大，其换热效果越好。图15 为第8 周期内不同振幅下Nu数随时间的变化规律，可以看出，不同振幅操作条件下Nu数随时间的变化规律基本一致，但在较大振幅操作条件下Nu数明显大于在较小振幅操作条件下的Nu数，即在较大振幅条件下流体与恒温壁面之间的传热效果更加显著。 图16 为振荡流结晶器流动摩擦阻力系数随时间的变化图。可以看出，振荡流结晶器在较小振幅操作条件下的阻力系数大于较大振幅操作条件下的阻力系数，这是因为在较小振幅操作条件下流体的平均流速较小。通过观察图16 还可以发现，阻力系数随时间的变化曲线在1.45 与1.55 s 左右时，都有一个明显的突起，这是由于流体回流使管内流体的平均流速较小导致的（对比图14）。振荡流结晶器的振荡流和挡板，在强化换热的同时也增加了流动阻力，如果流动阻力太大，不仅会增加泵功消耗，甚至会因流速降低而削弱流体换热；相反，如果流阻和功耗较小，则意味着换热器的流动工况较佳，与之相应的换热效果也会较好。因此振荡流结晶器的强化传热设计应包含两个方面，一是强化对流换热；二是减少流动阻力[15]。为了反应强化传热效果，可采用PEC值评价系数评价其综合性能，PEC值越大，振荡流结晶器综合性能越好[16]，表达式如下：

图16 振荡流结晶器阻力系数随时间的变化图 Fig.16 Changes of drag coefficient with time

在x为10 mm 下的Nu和λ为基准，即公式（8）中的Nu0和λ0，分别用x为10，20，30，50 和100 mm下的Nu和λ与x在10 mm 进行对比得到相应的PEC记为PEC-0，PEC-1，PEC-2，PEC-3 和PEC-4。图17 为PEC值随时间变化图，计算周期内各个PEC的平均值分别为PEC-0 为1，PEC-1 为2.53，PEC-2 为4.74，PEC-3 为6.53，PEC-4 为16.98，通过对比不同振幅操作条件下的PEC平均值可以认为振幅增加，传热效果提高。

图17 PEC 值随时间变化图 Fig.17 Changes of PEC with time

6 结 论

a）从网格独立性及流动变化规律稳定性两个方面对模型进行验证。在网格独立性验证中，壁面热流密度的数值研究结果表明当网格数量为123 552 时足以达到精确计算的目的；而在流动稳定性验证中，壁面热流密度及Nu数数值研究结果表明在第3 周期开始达到稳定。

b）通过对具有周期性速度边界的振荡流结晶器在一个周期内的速度矢量图进行分析，得到了振荡流动流体的运动规律，并对比了不同振幅下相同时间点的速度矢量图，发现振荡所产生的漩涡随振幅的增大而增大，但当振幅大于单元腔室高度时，矢量图中的漩涡变化不明显。

c）不同振幅下第1，4，8 和11 腔室中心点温度随时间的变化均呈波浪式下降，振幅越大，观测点温度达到稳定的时间越短、振荡流结晶器轴向降温速率越快，而恒温壁面与流体之间的传热主要集中于边界层处，流体的温度受径向速度的影响剧烈。

d）振荡流结晶器在一个振荡周期内均存在正压差及负压差，振幅越大，流体平均流速越大，进出口压差就越大。

e）振荡流结晶器在较大振幅操作条件下Nu数明显大于在较小振幅操作条件下的Nu数，即在较大振幅条件下流体与恒温壁面之间的传热效果更加显著，在较小振幅操作条件下的阻力系数大于较大振幅操作条件下的阻力系数，通过PEC评价系数对振荡流结晶器换热特性进行综合评价，结果表明振幅越大，传热效果越好。