声源聚集度的波叠加法虚拟源强配置

王玉江，廖 阳，向 宇，李晓妮，林贤坤

(1.广西科技大学 广西汽车零部件与整车技术重点实验室，广西 柳州 545006；2.广西柳州福臻车体实业有限公司，广西 柳州 545003)

0 引言

波叠加法最初是由文献[1]提出的，假设实际声源可用辐射体内一定数量的虚拟声源来替代，进而拟合出实际声场。但虚拟源强的配置方法影响声场重建的精度[2-3]，优化配置虚拟声源对提高声场重建精度具有一定的意义。

目前对于虚拟源强配置方法的研究，按照所采用等效源的不同可以分为两类：采用简单源(单极子或偶极子等)作为等效源和采用球面波作为等效源。在采用简单源作为等效源研究方面，等效源分布在实际声源表面背离分析域一定距离的虚源面上,且等效源的个数等于表面节点数时，数据仿真结果最佳[4-5]。但对于结构复杂的振动体，特解源配置的选择存在一定的局限性。在采用球面波作为等效源研究方面，实际辐射声场用不同阶次的球面波源近似代替,按照傅里叶级数展开，应包含所有阶次的球面波源,而为了计算的方便，需进行截断处理，选取最优的展开项数是等效替代的重点[6-7]。文献[8]采用多球形虚拟源强替代振动体近场声场，有效地解决了球面波有限阶数截断的问题。文献[9-10]将统计最优的方法应用于近场声全息，提出了一种适用于平面测量的柱面波函数近场声全息方法。文献[11]通过改变测量孔径与测点数，提出一种基于稀疏贝叶斯学习的高分辨率近场声全息方法。但以上方法均没有克服虚拟源强配置中简单源分布与声源表面的共形问题，而为了将波叠加法应用于任何结构和形状的振动体，需要适用性较高的虚拟源强配置方法。

本文采用多球形虚拟源强作为等效源，根据各个点源的位置坐标，将各点声源的声压值作为权值，预置一定的搜索半径，计算出以每个声源为中心的声源聚集度，并按照声源聚集度进行归类分析。然后通过重心法求出虚拟源强的球心坐标，进而实现虚拟源强的配置，克服了采用简单源分布与声源表面的共形问题，更适用于结构复杂的振动体。

1 声源聚集度的聚类分析法

区别于以往采用单个虚源面的形式，本文采用多个球形虚源面，同时将多个球形虚源面的中心放在与测量面平行的平面上，以减小虚源面与源面的非共形引起的误差[12-13]。多球形虚拟源强配置面与测量面的布置图如图1所示。当配置n个虚源面时，任意一点P的声压可由叠加原理和虚拟源强技术[14]得出：

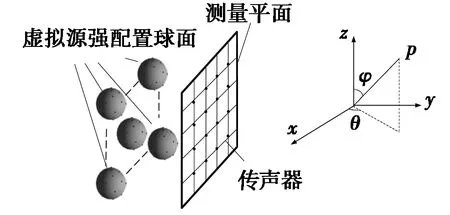
图1 多球形虚拟源强配置面与测量面的布置图

(1)

将虚源面上的源强密度函数沿子午线方向和周向展开，可得：

(2)

将式(2)代入式(1)，可得：

(3)

根据等效源强理论，利用矩形积分计算式(3)中的积分，并代入式(1)，可得：

(4)

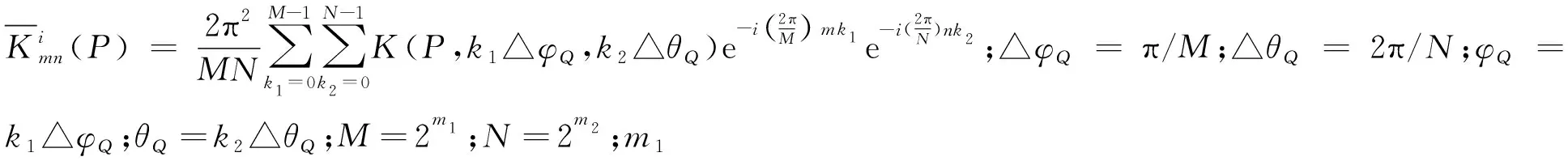
在以往的声源分析中，采用的声源分布并不是随机的，是按照一定的规律进行分布的。而对于任何结构和形状的振动体，由于声源产生是随机分布的，需要根据声源的空间聚集度分布特性进行虚拟声源的布置。聚类分析将抽象对象的集合分组为多个类，且每一类由类似的对象组成，其目的是在相似的基础上收集数据来归类[15-16]。声源聚集度可以定义为：不规则振动体内，单位体积内聚集的实际声源的数量和大小的规模。声源的空间聚集度主要反映不规则振动体内实际声源的数量和大小聚集的程度。本文假设声源的数量和大小对一定区域的声源聚集度的影响是同等重要的，各占一半，则定义某区域的声源聚集度F为：

(5)

其中：a为单位体积内的点声源数量；A为声场系统内总的点声源数量；b为单位体积内点声源的声压值之和；B为声场系统内点声源的声压值之和。

2 波叠加法的虚拟源强配置原理

文献[8]依据重心法的原理，解决了多球域波叠加法的虚拟源强的选址问题。本文以每个声源为中心，预置一定的搜索半径d，根据声源聚集度进行归类分析，计算出以每个声源为中心的声源聚集度，并遴选出最大的声源聚集度。然后，将搜索半径内的声源剔除，并在预置搜索半径d内重新搜索，遴选出次优的声源聚集度。一直循环搜索至剩余的声源聚集度小于10%时，剩余的点声源以点源进行替代，进而将虚拟声源分为质心球虚拟源强、非质心球虚拟源强和点声源3类。

按照声源聚集度进行聚类分析，将多球形虚拟源分为质心球虚拟源强和非质心球虚拟源强两类。其中，质心球虚拟源强球心坐标[8]为：

(6)

其中：(xi,yi,zi)为各点声源的坐标；p(xi,yi,zi)为点声源(xi,yi,zi)的声压值；v为点声源的数量。

根据声源聚集度的聚类分析结果，将属于同一类别的点声源构成一个子系统，同样通过重心法求出各个子系统的重心坐标，作为非质心球虚拟源强的球心坐标，可以表示[8]为：

(7)

3 仿真结果分析

在加入信噪比为20 dB的高斯白噪声情况下，本文假设测量面的一侧为不规则振动体，其中，S为25个点声源组成的任意形状的振动体，分布在0.4 m×0.8 m×0.8 m的长方体内。坐标原点设在测量面中心位置，x轴为测量面指向声源S的轴向方向，测量距离初始值l=0.8 m，测量面声源采用8个× 8个的声阵列布置方式，仿真对象示意图如图2所示。

设置搜索半径d=0.2 m，采用聚类分析法计算区域内声源的聚集度，结果如表1所示。根据声场聚集度进行搜索归类后，其中，区域1～区域4的声场聚集度分别为40%、24%、16%和12%，而剩余的两个散点距离较远，用独立的点声源进行替代。进而采用聚类分析法将25个点声源分为6个区域，其中，区域5与区域6均只包含一个点声源。

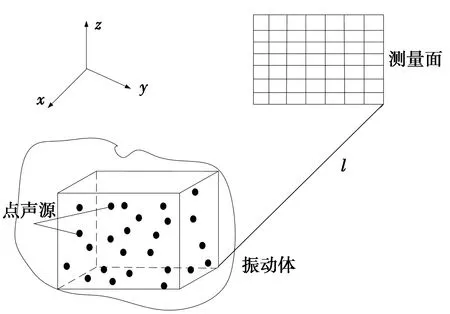
图2 仿真对象示意图

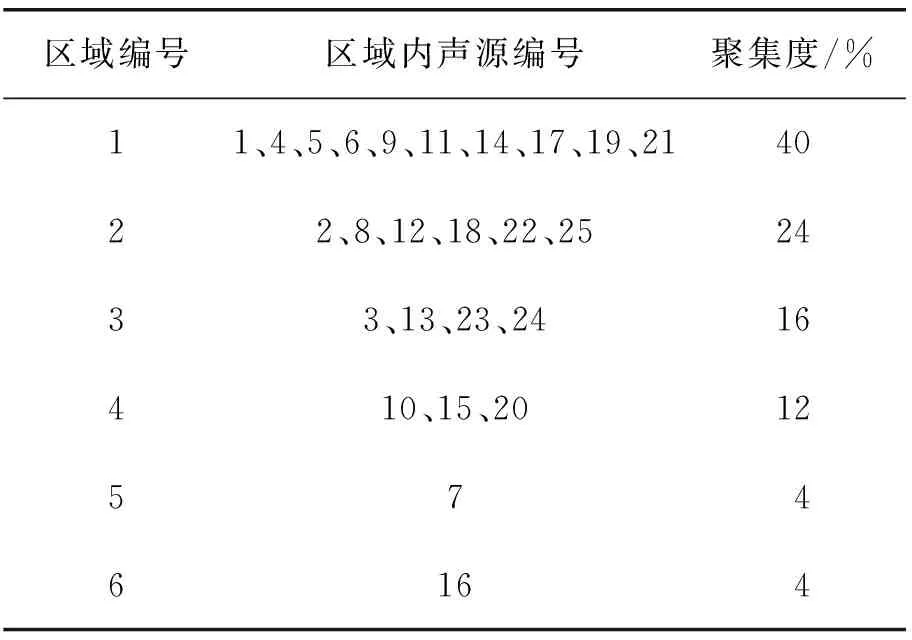
表1 采用聚类分析法得到的声源聚集度

利用式(3)求出整个系统的重心，假设质心位置虚拟球的半径r0=0.05 m。然后，根据聚集度的大小，采用不同半径的球形虚拟源强替代区域内的实际声源，其中，区域1～区域4分别用半径为0.100 m、0.050 m、0.030 m和0.025 m的球形虚拟源强替代，而仍用两个散点对实际声源7和声源16进行声场计算。利用式(4)求出区域1～区域4内非质心球虚拟源强的重心。

声压幅值重建结果与误差图如图3所示，初相位重建结果与误差图如图4所示。

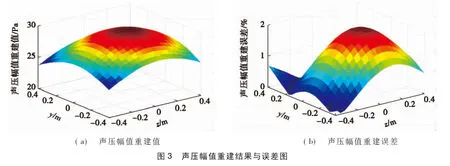
由图3a可以看出：声压幅值重建值与实际声压幅值理论值比较接近。由图3b可以看出：声压幅值重建误差的最大值为1.812%，声压幅值重建误差最大值分布在质心球虚拟源强正对的位置，出现位置与文献[8]一致，但重建精度比文献[8]的(声压幅值误差最大值为5.396%)要高。

由图4a可以看出：声压初相位重建值与实际初相位幅值理论值比较接近。由图4b可以看出：初相位重建误差的最大值为1.617%，初相位重建误差最大值出现在振动体的边界位置，且误差有一定的激变，这是由于采用两个散点对实际声源替代所导致的。初相位重建误差比较大的区域分布在非质心球虚拟源强正对的位置，这与文献[8]一致，但重建精度比文献[8]的(初相位重建误差最大值为4.547%)要高。

通过采用质心球虚拟源强和非质心球虚拟源强的配置，对不规则振动体的聚集度比较高的声源进行替代，而对于振动体离散的声源采用点声源进行替代。采用两种声源相结合的方法，克服了采用简单源配置与声源表面的共形问题，更适用于结构复杂的振动体。

4 结论

(1)在基于多球域波叠加法理论的基础上，提出了声源聚集度的聚类分析法，并与重心法相结合，改进了原有的虚拟源强配置方法。在加入信噪比为20 dB的高斯白噪声情况下，声压幅值和初相位的误差均小于2%，证明了该方法的有效性。

(2)通过采用3类虚拟源强(质心球虚拟源强、非质心球虚拟源强和点声源)的配置，克服了采用简单源配置与声源表面的共形问题，更适用于结构复杂的振动体。

(3)声源聚集度的聚类分析法，在优化配置质心球虚拟源强、非质心球虚拟源强和点声源虚拟源强关系上取得了一定的突破，为进一步研究虚拟源强的合理配置提供了理论依据。