利用声压有效值信息进行白噪声声源识别

罗瀚波，赵晓丹，周海川，赵秀亮

(江苏大学汽车与交通工程学院，江苏 镇江 212013)

0 引 言

近年来随着计算机计算能力与信号处理技术的不断进步，基于传声器阵列信号处理的声源识别方法[1-3]取得了较大发展，其中主要包括波束形成方法[4-6]与近场波束形成技术[7-8]，传统波束形成通过对信号进行相位对齐与累加求和来判断声源位置，近场声全息需要使用阵列在近场测量声全息信息，经声场空间变换实现声场重建与正向预测，以上两种方法在计算过程中都需要用到声压相位信息，在工程实践中存在声源辐射白噪声信号的情况，对其诊断是有需求的，白噪声[9]是不相干的信号，没有相位，无法使用基于声信号相位的声源识别等方法进行识别，目前国内外针对此类白噪声的声源识别研究少，尚未看到文献报道。

本文提出利用声压信号有效值进行内积运算识别白噪声声源，以典型的球面波声源[10]为对象，分析推导利用声压信号有效值识别白噪声的方法，继而建立声源识别步骤，首先研究对单个声源的识别，继而研究多个点源的识别，通过仿真计算与实验对本方法进行验证。

1 理论分析与识别步骤

本文以球面波为例来进行声源识别研究。假设在阵列面的上方空间内存在一个辐射白噪声的球面波声源 S，示意图见图1，球面波声源 S的声压信号有效值P与传播距离满足如下关系：

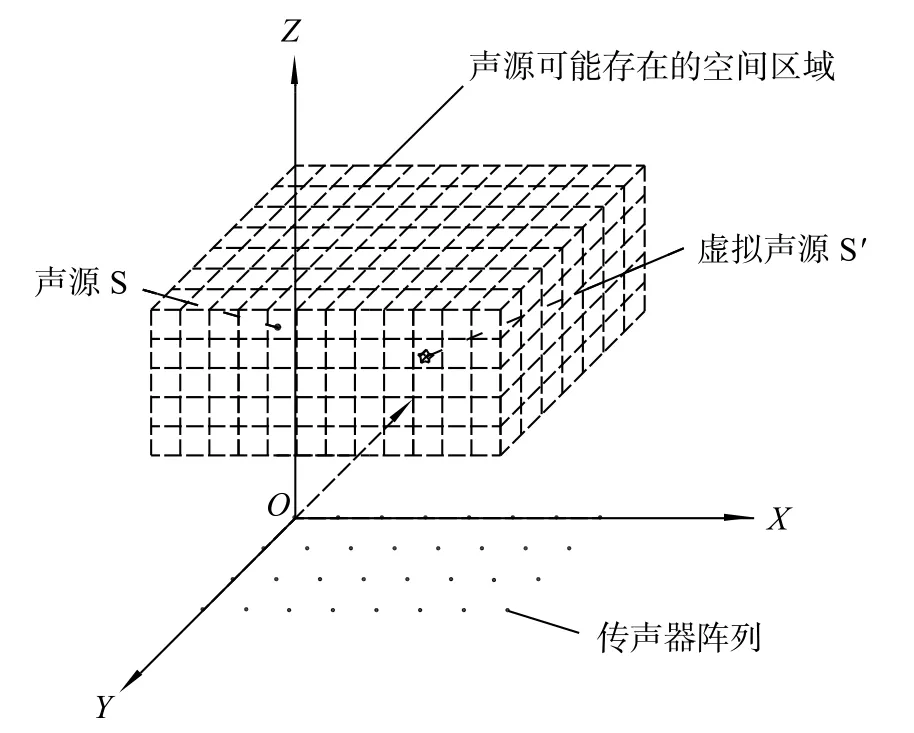
图1 利用声压有效值进行声源识别示意图

式中：Q——声源强度；

r——接收点到声源的距离。

基于以上理论分析进行声源识别，建立识别步骤，绘制识别步骤流程图如图2所示。

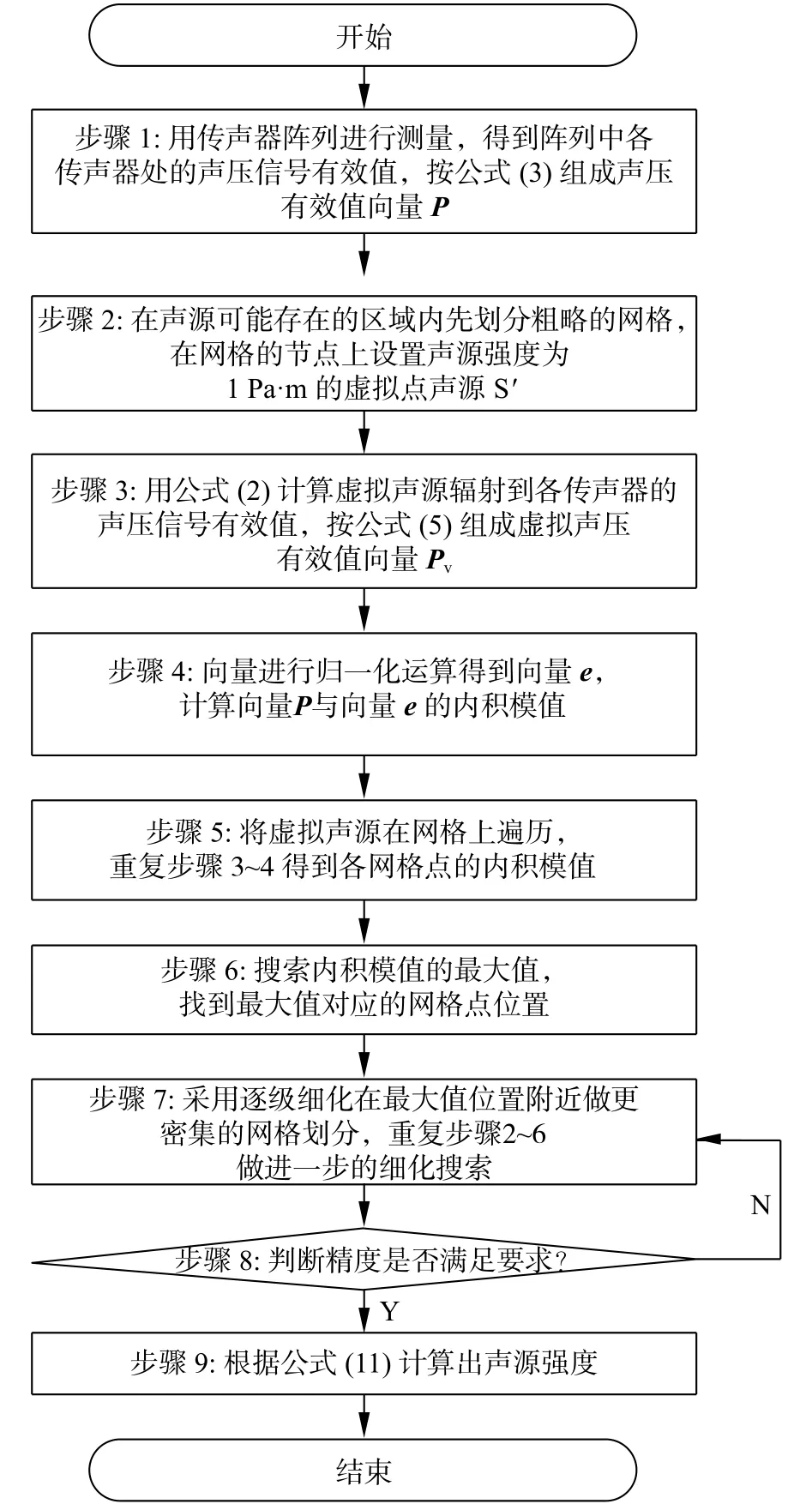
图2 识别步骤流程图

2 单个白噪声声源识别

首先对单个辐射白噪声的点声源进行识别。

设声源面距离测量面1 m，声源理论位置为(0.6359，0.5688)m，声源辐射强度为6 Pa · m的白噪声。使用11×11的传声器阵列进行测量，传声器间距为0.1 m×0.1 m。观察声源面上内积模值的分布情况，如图3所示，内积模值最大值处与声源位置基本一致。

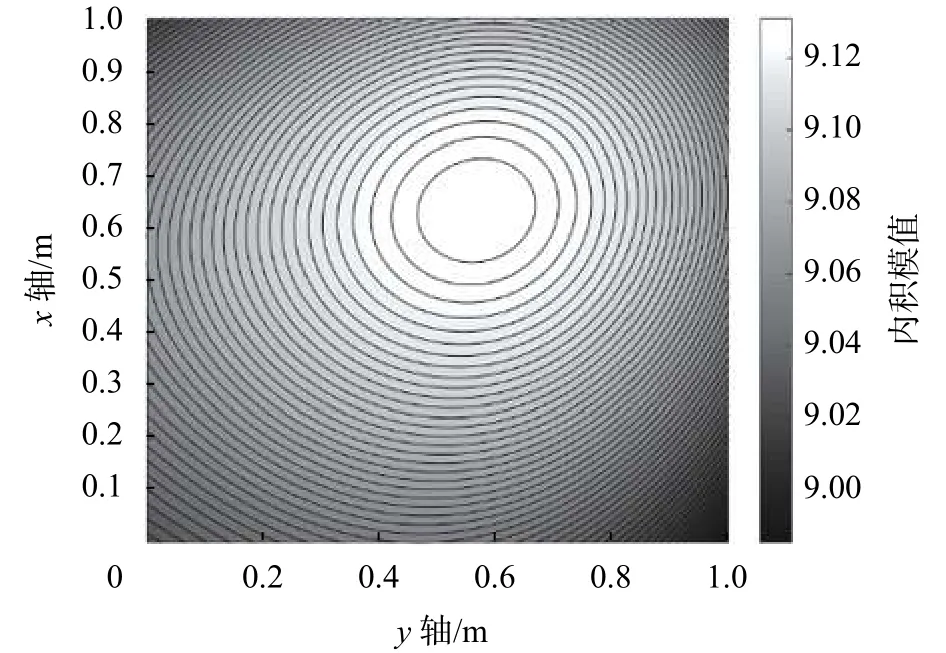
图3 声源面上内积模值分布图

使用前面的步骤进行识别，识别结果见表1。可以看出，该方法识别出的声源位置与强度准确。使用本文方法可以准确识别出声源面上的单个白噪声声源。

表1 平面上点声源识别结果

在工程中测量白噪声信号有效值时会存在误差，前面没有考虑这种误差的影响。下面考虑测量误差和测量距离的影响，将前面算例中声源与测量面之间的距离设为 0.5 m、1 m、2 m、5 m，同时在向量P中加入15 dB随机噪声模拟测量误差对声压有效值的干扰，观察此时的识别情况，结果如表2所示。

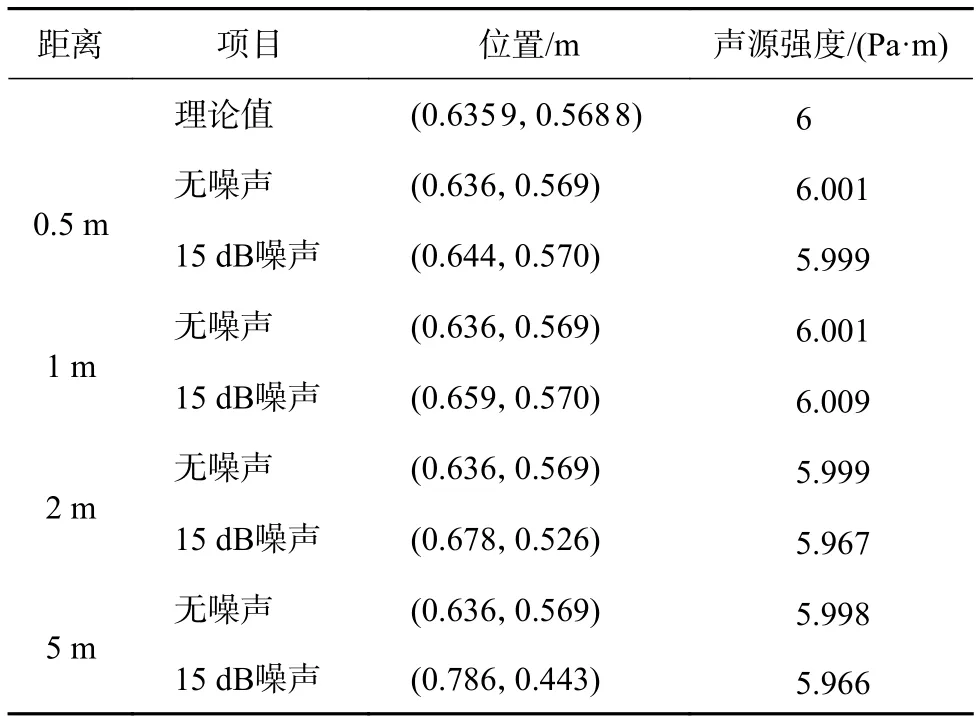
表2 识别距离与测量误差对识别效果的影响

从表2可看出：不考虑测量误差，测量距离远、近都可以做到准确识别。加入干扰噪声后，测量距离为0.5 m、1 m时的识别误差小，测量距离增大到2 m时误差增加，当测量距离增大到5 m时，识别误差大，这是由于当声源与测量面之间的距离很大时，各测量点处声压有效值的差异很小，容易受到噪声干扰的影响，导致识别结果出现大的偏差。

由于本文方法不使用相位信息，因此在传声器布置时有一个便利：不需要考虑传声器布置间距的限制[12]，针对测量距离增大后识别误差大的情况，可以通过调整阵列中各传声器之间的间距增大来改善识别效果，将仿真算例中传声器之间的间距增大到0.3 m，干扰噪声仍然是15 dB，声源面与测量面之间的距离是5 m，声源识别结果如表3所示。

表3 传声器间距对识别效果的影响

由表3可知，当传声器间距增大后，识别结果准确。

前面分析的是平面上的白噪声声源识别，下面用该方法对空间中的点声源进行识别。设声源位于 1 m×1 m×1 m 的空间区域内，传声器阵列与识别区域下表面之间的距离是0.2 m，声源理论位置为(0.5356，0.4685，0.7354) m，声源辐射白噪声的强度为6 Pa · m，同时观察噪声影响，用15 dB的随机信号模拟测量误差对声压有效值的干扰，识别结果如表4所示。

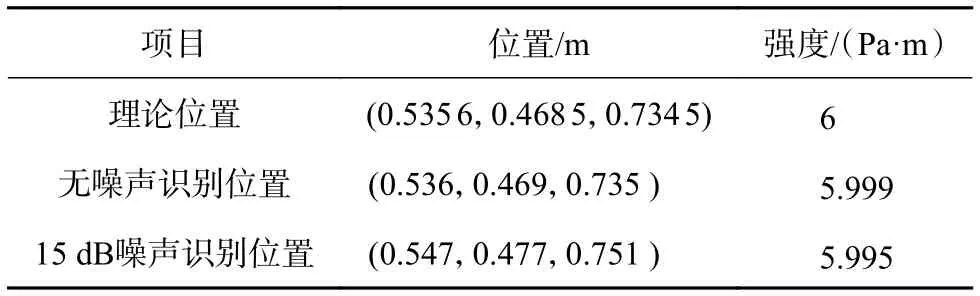
表4 空间中白噪声声源识别结果

由表4可知，在信噪比为15 dB的情况下，识别出的声源位置与强度与理论值之间出现一定偏差，但在工程测量可以接受的范围之内。

3 多个白噪声声源识别

设声源面上存在两个辐射白噪声的声源 S1与 S2，强度分别为 2 Pa·m 和 4 Pa·m，对应的声源间距为0.6 m、0.4 m、0.2 m，声源 S1与 S2的具体位置见表5，利用迭代方法进行识别，迭代10次后识别结果如表5所示。

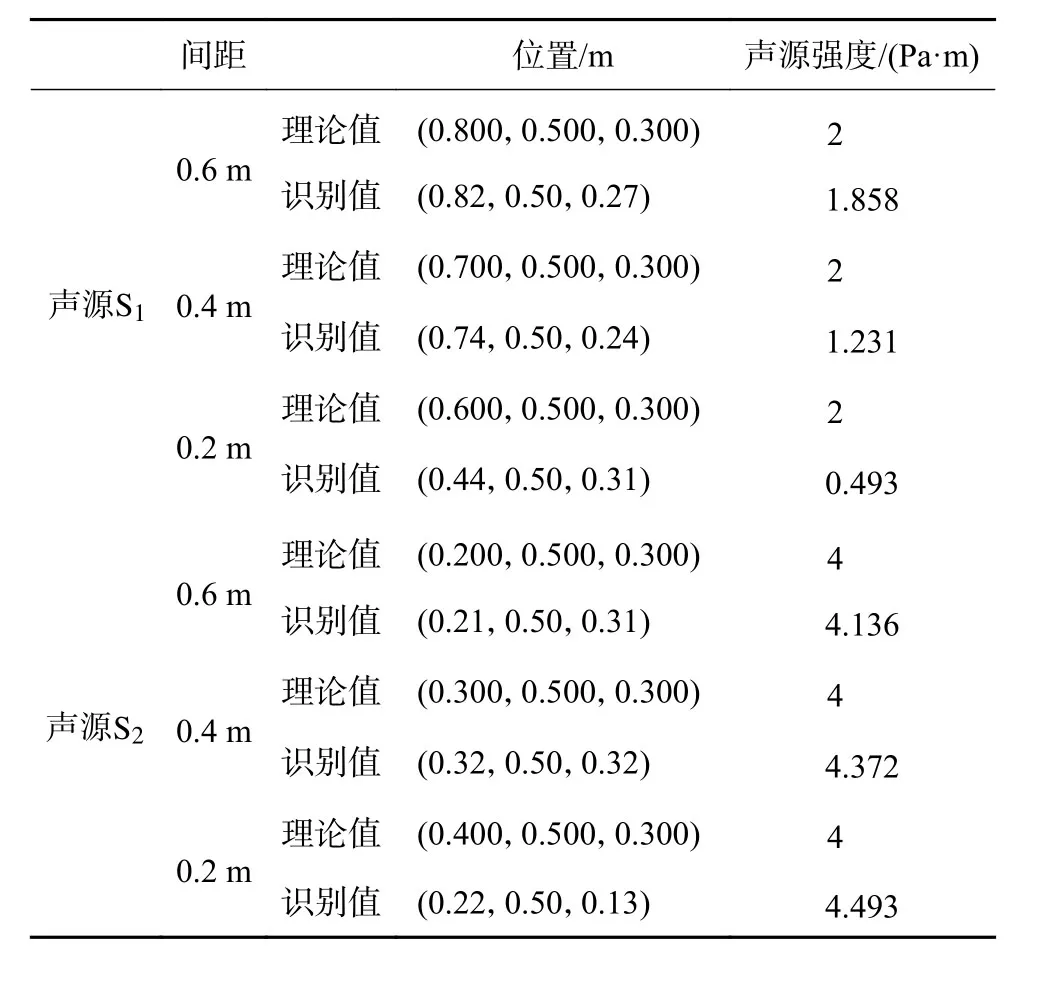
表5 声源间距对循环迭代识别多点声源的影响

由表5可知，当声源间距为0.6 m时，循环迭代10次可以较准确地识别出声源信息；当声源间距等于0.4 m时，迭代10次后的声源识别结果有一定误差；当声源间距等于0.2 m时，迭代10次后的声源识别结果偏差很大，这是因为当声源位置十分接近时，声源之间互相干扰严重，使得无法识别。

下面使用本文方法结合施密特正交对距离较近的两点声源进行识别，设声源面距离测量面1 m，声源面上存在两个声源S1与S2，声源强度分别为2 Pa·m和4 Pa·m，将声源 S1与 S2之间的距离分别设为0.2 m和0.1 m，；两个声源的具体坐标见表6。使用11×11的传声器阵列进行测量，传声器间距为0.1 m×0.1 m，识别结果如表6所示。

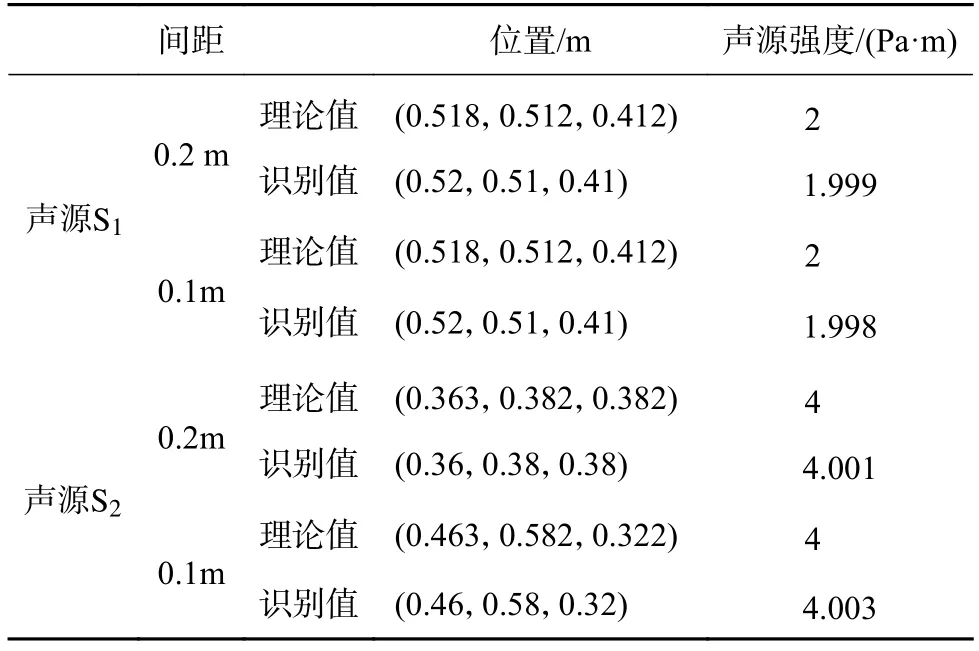
表6 利用施密特正交识别多点声源结果

从表6中可以看出，在两种声源间距的情况下，该方法识别出的声源位置与声源强度均准确。使用施密特正交消除了声源之间的相互干扰，即使在声源之间距离较近时，也能取得良好的识别效果。

为了考察测量误差产生噪声对多点声源识别的影响，在向量P1,P2加入信噪比为15 dB的干扰噪声，观察加入噪声以后的识别结果，声源之间的距离是0.1 m。

由表7可知，测量误差带来的噪声干扰对识别结果产生了一定影响，但仍然可以做到有效识别，因为施密特正交本质上是一种内积运算，具备一定的抗干扰能力，因此即使在距离0.1 m的情况下，也可以消减相互干扰，进行多点声源的准确识别。

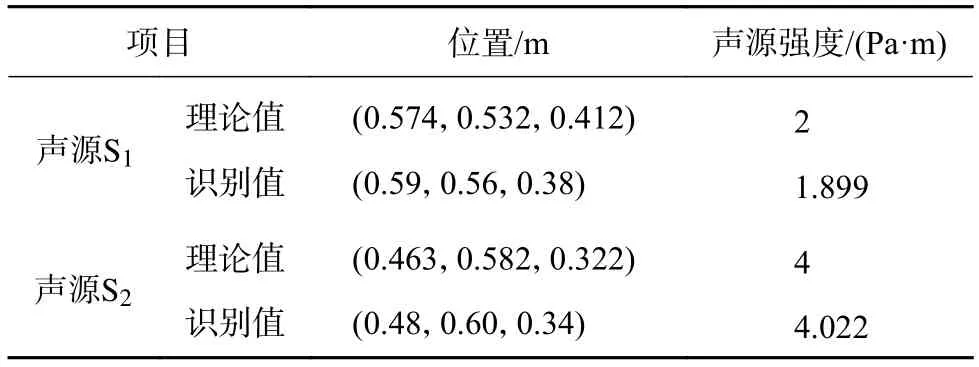
表7 噪声干扰对识别两点声源的影响

4 实验验证

在半消声室内进行实验，实验装置的示意图与现场照片如图4和图5所示，球声源球心与阵列之间的距离为 1 m，球声源的空间坐标是（1.10，0.45，1.00） m。使用YG201型传声器组成的4×8通道阵列进行测量，传声器间距为 0.3 m×0.3 m。控制OS003型无指向型球声源产生白噪声信号，使用信号采集系统进行采集，采样频率为51200 Hz。在开始识别声源前，选择阵列中3个典型位置的传声器，一个位于阵列中部，传声器序列号为 M34；两个位于传声器阵列边角，传声器序列号为 M18和 M41，3个传声器测得的声压信号有效值分别为 0.1241 Pa 、0.0801 Pa 和 0.1042 Pa，根据球面波辐射关系公式（2）分别计算出声源强度并取平均，获得声源强度Q为 0.1291 Pa·m，将此声源强度值作为标准与识别声源强度进行对比。

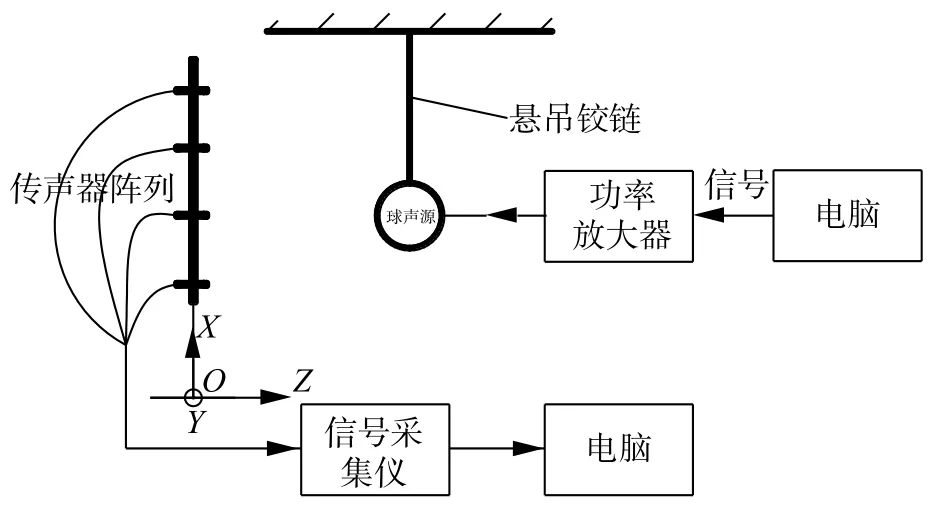
图4 声源识别装置示意图

图5 实验现场照片

对辐射白噪声的球声源进行识别，观察距离阵列1 m平面上的内积模值分布情况见图6，可以看到峰值位置出现在声源位置附近。识别出声源位置后，由公式（11）计算得到声源强度，声源识别实验结果如表8所示。

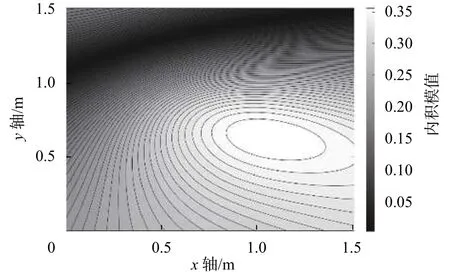
图6 内积模值等值线图

表8 点声源识别实验结果

由表8的识别结果可看出，沿各坐标轴方向的识别误差均小于0.05 m，声源强度误差为2.47%，识别出了白噪声声源的位置与强度。

5 结束语

1）辐射白噪声的声源没有相位信息，无法用波束形成方法进行识别，本文提出一种利用声压有效值信息进行声源识别的方法，建立了相应的识别步骤。

2）利用本文方法对点声源进行识别，在没有噪声干扰的情况下，测量距离远近都可以准确识别，考虑测量误差后，有噪声干扰，测量距离远时的识别结果误差大，可以通过增大传声器之间的间隔提高识别精度。

3）当声源间距较远时，利用本文方法结合迭代可以进行多点声源的识别；当声源间距较近时，提出引入施密特正交方法来消除声源之间的干扰，可以准确识别出各声源信息。

4）在半消声室内用OS003型球声源辐射白噪声信号，使用本文方法对声源位置和强度进行了识别，验证了该方法的有效性。

5）本文方法无需使用相位信息，阵列中各传声器之间间隔不受限制，测试过程中无需进行相位匹配，测量方便，测试成本低。