稳涡内构件对旋风分离器内流场和性能的影响

沈 聪，董振洲，王佳音，杨景轩，郝晓刚

(太原理工大学 化学化工学院，太原 030024)

高效率和低压降一直是旋风分离技术开发追求的目标。随着持续不断的改进，现代高效旋风分离器已能基本除净粒径大于10 μm的颗粒，但对于5 μm以下的超细颗粒的捕集能力仍需进一步挖掘。目前，国内外学者通过实验和数值模拟的方法对旋风分离器内颗粒运动进行研究，发现排尘口颗粒返混夹带现象是超细颗粒逃逸的主要因素之一。因此，深入地认识颗粒的返混夹带现象对旋风分离器结构参数的设计优化具有十分重要的意义。

黄学东[1]通过实验方法研究颗粒返混夹带问题，发现颗粒返混夹带主要影响内旋流区域的颗粒浓度，内旋流对返混颗粒具有一定的二次分离作用。韩恒标等[2]通过实验方法研究了PSC型旋风管排尘锥内颗粒浓度分布，发现开缝的排尘结构具有二次分离作用。万古军等[3]、薛小虎等[4]、宋健斐等[5]从数值计算的角度去研究颗粒返混问题，发现排尘口附近存在明显的颗粒返混。孙涛[6]通过实验回归分析得到灰斗返混量的计算公式，计算得到的总效率与实验得到的总效率误差在0.79%以内。上述研究揭示了影响颗粒返混的因素，但并未说明颗粒返混的形成原因。祝华腾等[7]对不同结构的旋风分离器二次涡的数值模拟和分析发现排尘口处的局部旋涡流动会对颗粒返混产生影响。元少昀等[8]、吴小林等[9]通过实验研究发现旋进涡核现象能够引起这种局部流动。旋风分离器全空间内都存在旋进涡核现象，但涡核的运动频率会随轴向位置而变化，并在排尘口达到最大[9-11]。因而，旋进涡核会将部分已被壁面捕集的颗粒重新带入内旋流，造成大量颗粒的返混逃逸[12]。KOSAKI et al[13]通过实验及CFD模拟的方法发现在分离器内部加入稳涡杆或在排尘口下方加入圆锥能够稳定旋风分离器内部流场，从而提高分离效率。吴小林等[14-15]、YOSHIDA et al[16-18]通过对相似内构件的实验与模拟研究，也得到类似观点。虽然众多学者发现了旋进涡核的旋转特性与颗粒返混存在联系，但是至今还鲜少有对于两者之间定量关系的研究。因此，深入研究涡核的旋转特性与颗粒返混的定量关系成为本文重点。

为了研究涡核的旋转特性与颗粒返混的定量关系需要排除旋风分离器的基本结构参数对涡核旋转特性的影响。通过KOSAKI et al[13]的研究发现，内构件能够有效地改变涡核的旋转特性。所以笔者选用圆锥作为稳涡内构件，通过对比在不同入口气速下有无圆锥的两个尺寸旋风分离器的内流场，来揭示涡核的旋转特性与颗粒返混的定量关系，并对分离效率和压降进行分析。

1 模拟方法及验证

1.1 边界条件

求解控制方程时压力速度耦合项采用SIMPLEC(semi-implicit method for pressure linked equations consistent)算法，压力梯度项采用PRESTO(pressure staggering option)方法进行处理，各对流项采用QUICK(quadratic upwind interpolation of convective kinematics)差分格式。由于旋进涡核现象是随时间变化的，采用非稳态模拟，时间步长选为2×10-4s.

入口气体为常温下的空气，入口边界条件为速度入口，分别给出垂直进入入口截面的时均速度值，速度大小分别为15，20，25 m/s，入口处设置相应的水力直径和湍流强度。出口边界条件设置为充分发展出口(outflow边界条件)，为保证充分发展条件的成立，计算中将旋风分离器出口段加长。气相流场在壁面采用无滑移边界条件。

两相流场模拟计算时，选用密度为2 700 kg/m3，粒径为1 μm的颗粒，在入口处的射流源采用面源，即颗粒由入口截面上的每一个网格的中心位置射入。颗粒的入口速度设定与气相入口速度相同；入口质量浓度取10 g/m3.

1.2 几何模型

图1展示了旋风分离器的基本结构型式。坐标系原点在顶板圆截面圆心处，旋风分离器的中心轴为Z轴，且方向向下为正，气体进入旋风分离器的方向为Y轴。Type-A旋风分离器是标准平顶蜗壳式旋风分离器，其内径为186 mm，筒体长180 mm，锥体长560 mm，矩形入口高度为110 mm，入口宽度为45 mm，排气管直径为90 mm，排气管下端与入口底端平齐。Type-B旋风分离器的结构参数与Type-A旋风分离器相同，区别仅是在排尘口处增加了圆锥。采用六面体结构化网格对计算区域进行离散，为了方便网格划分，将圆锥顶角去除，具体尺寸见图1.

1.3 模型验证

为了验证计算模型的准确性，与高翠芝等[19]文中筒体直径186 mm模型的试验结果进行了对比，模拟模型与其试验采用的旋风分离器模型完全相同，具体尺寸如上文所述，入口气速为20 m/s，进行模拟。对网格数目的无关性进行验证，通过对比筒体Z=100 mm处的速度沿径向的分布图，结果如图2，综合考虑精度和计算负荷，选取了网格数目为17万的网格为最终的模型，计算的总网格数为170 284.

图1 旋风分离器几何模型

图2 网格无关性验证

高翠芝等[19]采用点动态压力信号采集系统测量分离器各测点的压力，并利用快速傅立叶变换(Fast Fourier Transform，简称FFT)将测量到的原始时域信号转换成易于分析的频域信号(信号的频谱)，发现在分离器筒体及锥体段，分离器外旋流区压力信号没有明显的主频，而内旋流压力信号具有150 Hz的波动频率，因此，判定PVC的频率为150 Hz.

本文使用相近的手段分析涡核的运动频率。首先在排尘口截面建立一个虚拟面并监测它的面最小静压随时间的变化情况，这里认为面最小静压点即为涡核中心点，然后将这种变化记录下来。其次，对记录下来的数据进行快速傅立叶变换，得到频谱关系(如图3)。其中有一个主峰，对应的频率为152 Hz.模拟得到压力频谱特性与实验的基本相同，仅是峰值频率略低于实验观测。

此外，王璐等[20]提出利用监测面最小压力方法可以描述出排尘口横截面处涡核旋转一周的时间。本文利用王璐所提出的方法得到的涡核旋转一周的时间为0.006 8 s，与之对应的旋转频率为147 Hz，这与FFT得到的基本频率152 Hz非常接近，见图3.

图3 模拟验证结果图

2 结果与讨论

2.1 圆锥对切向速度与轴向速度的影响

本文通过对比在不同入口气速下，排尘口处有无圆锥的旋风分离器分离空间的切向速度来研究圆锥的加入对切向速度的影响。图4为Type-A与Type-B旋风分离器内流场的切向速度在不同轴向位置的分布图。由图可知，在整个分离空间内，Type-A与Type-B的切向速度分布曲线沿径向基本保持一致，为明显的双驼峰分布，各个位置处的速度值也基本相同。但是，在接近排尘口的地方，由于圆锥的约束，Type-B中切向速度分布的对称性明显优于Type-A，见图4(f).总体来说，圆锥对于分离空间中气流的切向速度影响较小。

图5为Type-A与Type-B在不同气速下轴向速度分布图，从中可以发现圆锥对于轴向速度影响主要存在于上行流中，特别是几何中心附近上行流速减小的现象(以下简称为滞流现象)，而对下行气流的轴向速度影响不明显。观察不同的轴向位置可以发现在筒体的几何中心附近，Type-B的轴向速度比Type-A的大；但是观察图5(f)可以发现，在靠近排尘口附近的区域，Type-A与Type-B的轴向速度分布有较大的差异，Type-A轴向速度的滞留层消失，而Type-B仍存在较明显的滞留层，且呈现较好的轴对称性。圆锥一方面减轻了分离空间上部的滞流程度，另一方面也扩大了发生滞流现象的区域。总体来看，圆锥并未明显改善分离空间内的轴向速度分布。

2.2 圆锥对短路流的影响

目前，国内外学者还很少研究圆锥对短路流的影响。笔者通过分析对比Type-A与Type-B的下行流量的变化来分析研究圆锥对短路流的影响。图6为不同气速下Type-A与Type-B的下行流量图，从图中可以发现，在轴向位置Z=110 mm到Z=135 mm之间，两个分离器内的下行流量都会突然减小，而这个位置正是排气管下放气流短路流出分离器的位置。圆锥的加入并不会改变短路流区的大小。统计这两个位置的下行流量之差即得到短路流量。在三个入口气速下，Type-A的短路流量分别是0.016 69 m3/s、0.021 06 m3/s和0.026 83 m3/s，Type-B的短路流量分别是0.015 74 m3/s、0.021 33 m3/s和0.026 22 m3/s.对应入口气速下，Type-B的短路流量与Type-A相差最多5.7%，变化很小。

图4 Type-A与Type-B的切向速度分布图

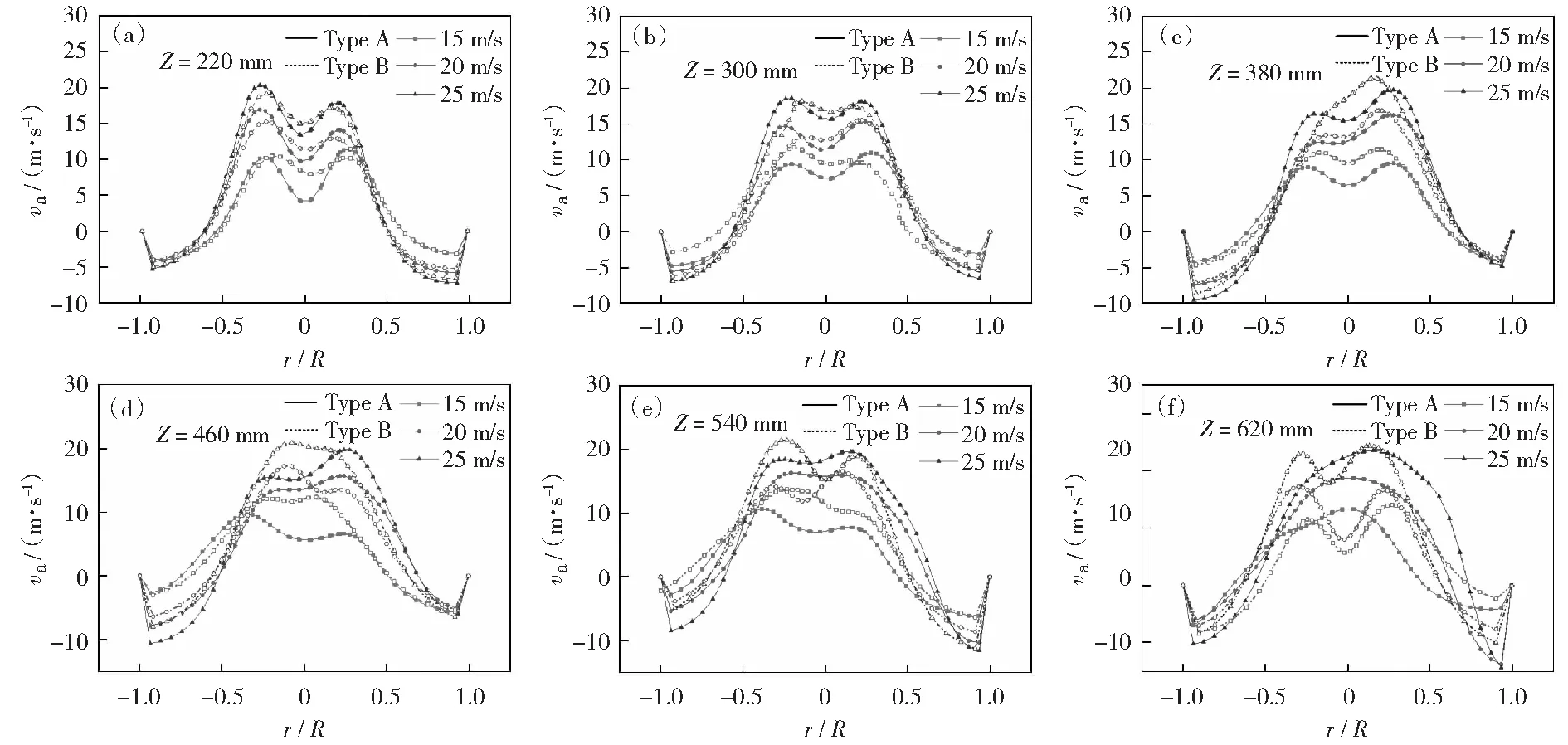
图5 Type-A与Type-B的轴向速度分布图

2.3 圆锥对旋进涡核旋转特性的影响

对旋风分离器Type-A与Type-B进行纯气相模拟，待其流场稳定后，得到涡核摆动的云图。图7为20 m/s下，Type-A与Type-B的纯气相条件下的静压分布图。可以看出Type-A中旋风分离器的旋涡尾端已经进入到了料腿中部，并且产生了很明显的摆尾现象；而Type-B的旋进涡核由于受到了圆锥的阻碍作用，无法进入料腿中，并且涡核尾端被牢牢固定到了圆锥上方，看不到明显的涡核摆尾现象。

在纯气相流场的基础上对两种旋风分离器内的气固两相流动进行模拟。计算过程中随时监测排气管出口的颗粒浓度，取浓度稳定之后2 s内的流场数据分析气固两相流场的非稳态性及颗粒捕集情况。

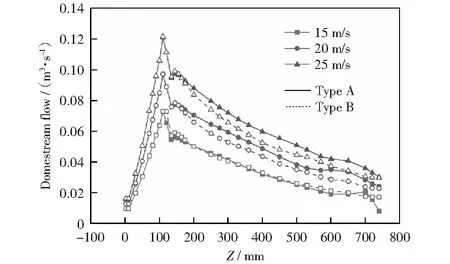
图6 Type-A与Type-B的下行流量图

图7 纯气相条件下的Y=0截面静压分布图

图8为Type-A与Type-B在气固两相下的静压云图。对比图7与图8可以发现，Type-A的两幅静压云图在插入管与分离空间差异较小，但是在排尘口与料腿处有较为明显的差异。在纯气相条件下，Type-A中的旋进涡核已经进入到料腿中，但是加入颗粒后可以明显发现它的自然旋风长变短了。

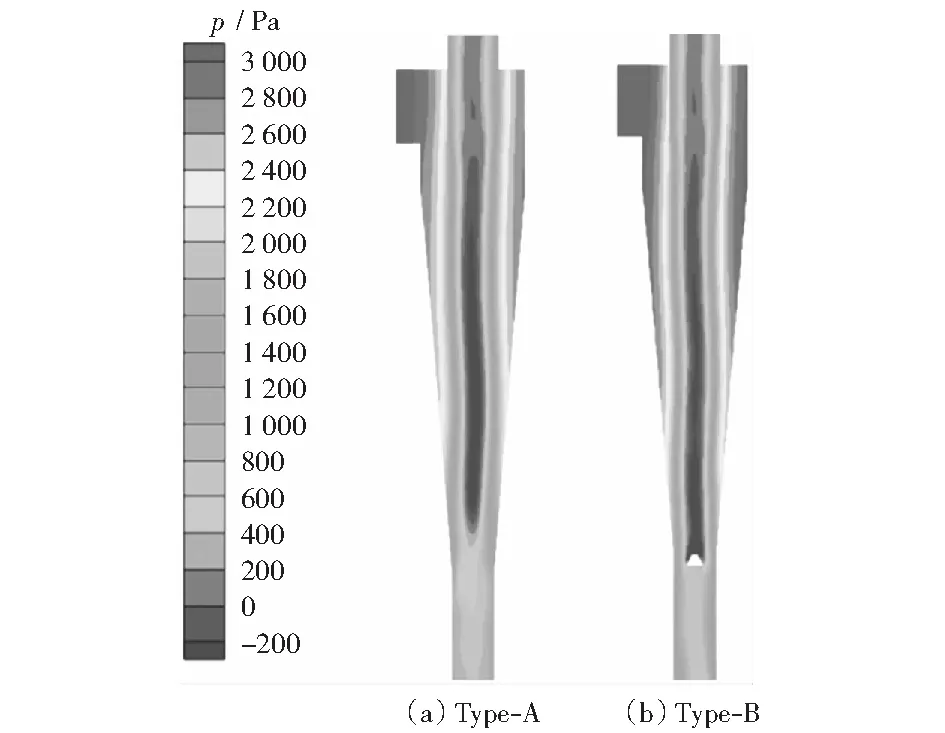
图8 气固两相共存稳定的Y=0截面的压力云图

同时，观察Type-B可以明显发现，加入圆锥后通入颗粒基本不会对自然旋风长造成影响，其旋进涡核依旧是被牢牢地固定在圆锥的上方。圆锥对于自然旋风长的影响很大。

图9 气固两相下排尘口截面涡核旋转特性图

2.4 涡核旋转特性对颗粒返混夹带率的影响

上文所开展的流场分析表明，圆锥的加入主要改变了旋进涡核的运动特性，而对各个分离效率理论模型所关注的外旋流区域的影响很有限。因此，有圆锥和无圆锥两种结构的捕集效率和颗粒逃逸情况的差别主要归因于旋进涡核特性的差别。由于短路流也会携带部分颗粒逃逸，因此，在旋风分离器的排气管正下方设置了如图10所示的监测面，分别统计短路流携带的颗粒(短路逃逸率)和上行气流夹带逃逸的颗粒(返混夹带率)。结果如表1所示。

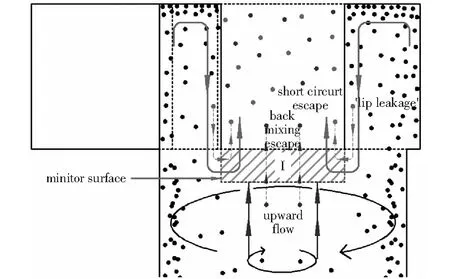
图10 颗粒逃逸的类型：短路流逃逸和返混夹带逃逸

表1 捕集效率、短路流逃逸率与返混夹带率

从中可以看出在各个入口气速下，Type-A的效率均逊于Type-B，加入圆锥后效率至少提高了20.9%。从颗粒逃逸情况看，圆锥的加入降低了短路逃逸的颗粒量，但影响非常有限，不足5%，而返混夹带的颗粒量则降低了大约20%，是提升捕集效率的关键，与涡核在排尘口处的运动特性密不可分。分离空间所捕集的颗粒汇聚于排尘口，而此处又是整个分离空间直径最小的部分，也是被捕集颗粒最靠近高速上行气流的地方。涡核内的压力是低于边壁处的，当其靠近边壁，在压差作用下边壁处的气流汇入，部分已分离的小颗粒受气流裹挟而进入上行流。如图9所示，Type-A中，涡核远离几何中心而非常靠近边壁，颗粒受气流裹挟而返混的几率大；Type-B中，涡核基本被固定在了圆锥上方，偏心幅度被极大的削弱，气流裹挟颗粒进入上行流的几率降低，另外，涡核旋转频率的降低意味着相同时间内涡核与壁面的接触减少，也有利于削弱颗粒因气流夹带而返混。

2.5 圆锥对压降的影响

压降是旋风分离器的另一性能指标，小压降意味着能量的节约。本文通过读取入口截面中心点和出口截面中心点的静压值，以两者的差作为旋风分离器的压降，结果如图11.从图中可以看出，随着气速的增大，压强呈线性增大的趋势，但是Type-A和Type-B的压降差值并不大，最大不超过200 Pa，不足压降的0.5%.因此，圆锥结构的加入在增加旋风分离器效率的同时并不会消耗额外的能量。

图11 两种结构的压降对比

3 结论

本文采用数值模拟方法研究了排尘口加入小圆锥对旋风分离器内流场与颗粒返混的影响，得到如下结论：

1) 排尘口处安放的圆锥可以改善其附近气流切向和轴向速度沿径向分布的对称性，但对分离空间大部分区域内气流的分布影响很小。

2) 在旋风分离器的排气管下方存在的气流短路逃逸现象不会因圆锥的加入而明显变化，相应的，颗粒随短路气流逃逸情况并没有明显改善。

3) 圆锥能够很好地抑制涡核偏离分离器几何中心的现象，降低已分离颗粒在气流裹挟下进入高速上行流的几率。相比未安装圆锥的结构，分离效率提升20%以上，同时压降没有明显增加。