充液圆管周向多股壁面燃气射流排水特性

胡雨博， 余永刚

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

0 引言

常规的水下枪炮发射方式通常为密封式发射或全淹没式发射[1-2]。密封式发射方式需要在每次发射前将身管内的水排出后密封炮口，使得炮口装置结构复杂，影响了火炮的发射速度。全淹没式发射方式是将身管直接淹没在水中，从而让炮口结构得到简化，但由于弹前空间充满水，弹前阻力急剧增大，使得膛内压力会随弹丸速度的增高而急剧上升，容易引发膛炸事故，为了提高发射安全性，弹丸初速通常较低。为实现水下枪炮高速发射，胡志涛等[3]提出了一种新的发射方式，即水下枪炮气幕式发射方式。该方式利用部分火药燃气在弹丸运动前将身管内的水实时排出，以形成气体通道，供弹丸在膛内运动，从而能够大幅度减小弹丸前的阻力。

气幕发展是典型的气体与液体相互作用的过程，对此国内外学者均进行了大量研究。Dai等[4]对音速和超音速条件下水下气体射流的流场特性进行了实验研究。施红辉等[5]通过实验证明了超音速射流的胀鼓和回击之间存在关联性。Weiland等[6]和Harby等[7]分别通过实验对垂直和水平射流入水过程中的射流夹断现象和射流边界不稳定性进行了研究。张焕好等[8]对超音速气体射流入水过程进行了数值模拟，分析了初始气泡的形成与形态的变化。上述研究均基于开放式液体环境，而对于射流在受限液体区域的研究，以液体发射药火炮为研究背景，有文献报道了燃气射流在液体工质中的扩展特性。莽珊珊等[9-10]和胡志涛等[11]通过实验及数值模拟方法，研究了储液室边界形状和喷孔结构等对单股高温燃气射流扩展的影响。Yu等[12]和Xue等[13]对双股燃气射流在渐扩型储液室中的掺混过程进行了研究。冯博声等[14]研究了边界形状对多股燃气射流扩展过程稳定性的影响。对于水下枪炮气幕式发射新方法，胡志涛等[3]设计了一种多孔结构弹丸，以此将部分弹后高温燃气引导到弹头前端进行排水，并通过实验探究了喷孔结构对射流扩展的影响。在此基础上，赵嘉俊等[15-16]改变了弹丸结构，将平面分布的喷孔改为锥形分布，并通过实验和数值模拟方法研究了喷孔结构变化对射流扩展以及排水性能的影响。周良梁等[17-18]通过实验研究与数值模拟方法分析了弹丸运动对射流扩展及排水性能的影响。但这种气幕生成方式会导致弹丸结构复杂、成本较高。

本文基于水下枪炮气幕式发射原理，通过在身管内壁设计若干道凹槽引导弹后燃气射流向前运动形成气幕，为气幕减阻发射提供一种新的途径，并对该方式下身管内气幕扩展过程以及排水特性进行了研究，为后续研究多参数变化以及弹丸运动对气幕形成及排水过程的影响做出铺垫。

1 理论模型

1.1 简化假设

针对高温高压的多股燃气射流在充液圆管中排水过程的特点，做出如下假设：1)将气体与液体相互作用视为三维非稳态过程，喷孔附近属于完全湍流状态；2)燃气为理想可压缩气体，且燃气射流在扩展过程中燃气组分保持不变；3)考虑到气体与液体相互作用时间短暂，可忽略液体工质汽化的影响。

1.2 数学模型

根据1.1节的假设，结合Navies-Stokes方程、流体体积函数(VOF)模型以及k-ε(k为湍动能，ε为湍动能耗散率)湍流模型，建立多股燃气射流在水下扩展的三维非稳态数学模型。

1)连续性方程

(1)

式中：α表示物质的体积分数，q=g、l分别表示气相和液相，αg+αl=1；ρ表示物质的密度(kg/m3)，其中ρl为常数；v为流体速度矢量。

2)动量方程

(2)

式中：p为静压(Pa)；ρ=α1ρ1+αgρg；μeff为有效黏性系数，μeff=μ+μt，μ为动力黏性系数，μt为湍流黏性系数；g为重力加速度矢量(m/s2)。

3)能量方程

(3)

式中：keff为有效热传导系数(W/m2)；E为流体总能(J)，

(4)

T为温度(K)，

(5)

4)燃气状态方程

p=ρRT，

(6)

式中：R为火药燃气常数，R=3.19 J/(mol·K)。

5)k-ε湍流模型

(7)

(8)

式中：Gk、Gb分别为速度梯度、浮力引起的湍动能；YM为可压缩湍流脉动膨胀对总耗散率的影响；C1ε、C2ε、C3ε、σk、σε为经验常数。

2 模型验证

为验证第1节理论模型的合理性，针对文献[19]中的实验进行数值模拟。模拟实验装置及模拟弹丸结构示意图如图1所示，充液圆管内径55 mm、长150 mm，8个贴壁喷孔沿模拟弹丸周向均匀分布，单个喷孔的形状均为2 mm×4 mm的矩形。实验利用电点火装置点燃燃烧室内的火药，使燃烧室内压力急剧升高，达到破膜压力时冲破紫铜膜片，高温高压燃气通过连接件，从多个狭缝形贴壁喷孔射入充满水的透明充液室中，形成了多股贴壁燃气射流，并随后在充液室内形成气幕，实验喷射压力为20 MPa.

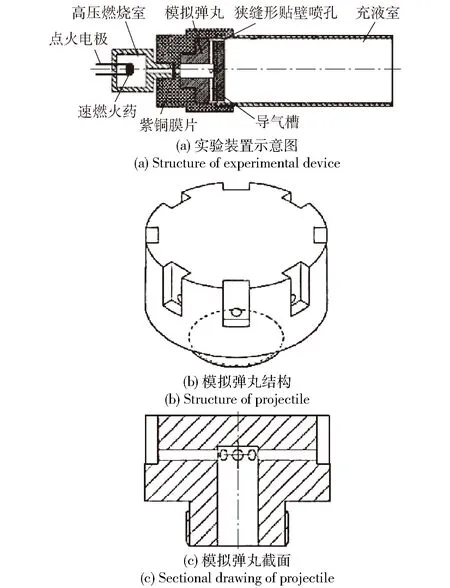
图1 实验装置和模拟弹丸结构示意图Fig.1 Structures of experimental device and projectile

对上述实验工况进行数值模拟，可得到射流气幕头部轴向位移l与时间的关系，如图2所示。由图2可见，模拟结果与实测结果基本一致，最大误差为4.86%，平均误差为3.52%，表明本文建立的数值计算模型基本合理。

图2 射流头部轴向位移计算值与实验值的对比Fig.2 Comparison between the calculated and experimental values of axial displacement of jet head

3 数值预测及分析

3.1 计算模型及网格划分

基于1.2节模型，对模拟弹丸运动前充液圆管周向多股壁面燃气射流的排水过程进行数值预测。图3所示为计算模型结构示意图。由图3可见，圆管内径30 mm、长1 000 mm，在内壁上均匀分布有8道凹槽，凹槽形状为3.5 mm×2.5 mm的矩形，凹槽长度与圆管长度相同，模拟弹丸为直径30 mm、长160 mm的圆柱体。由于模型的对称性，可取模型的1/16为计算域，网格总数约49万且在模拟弹丸表面进行了局部加密，并通过了网格无关性验证。

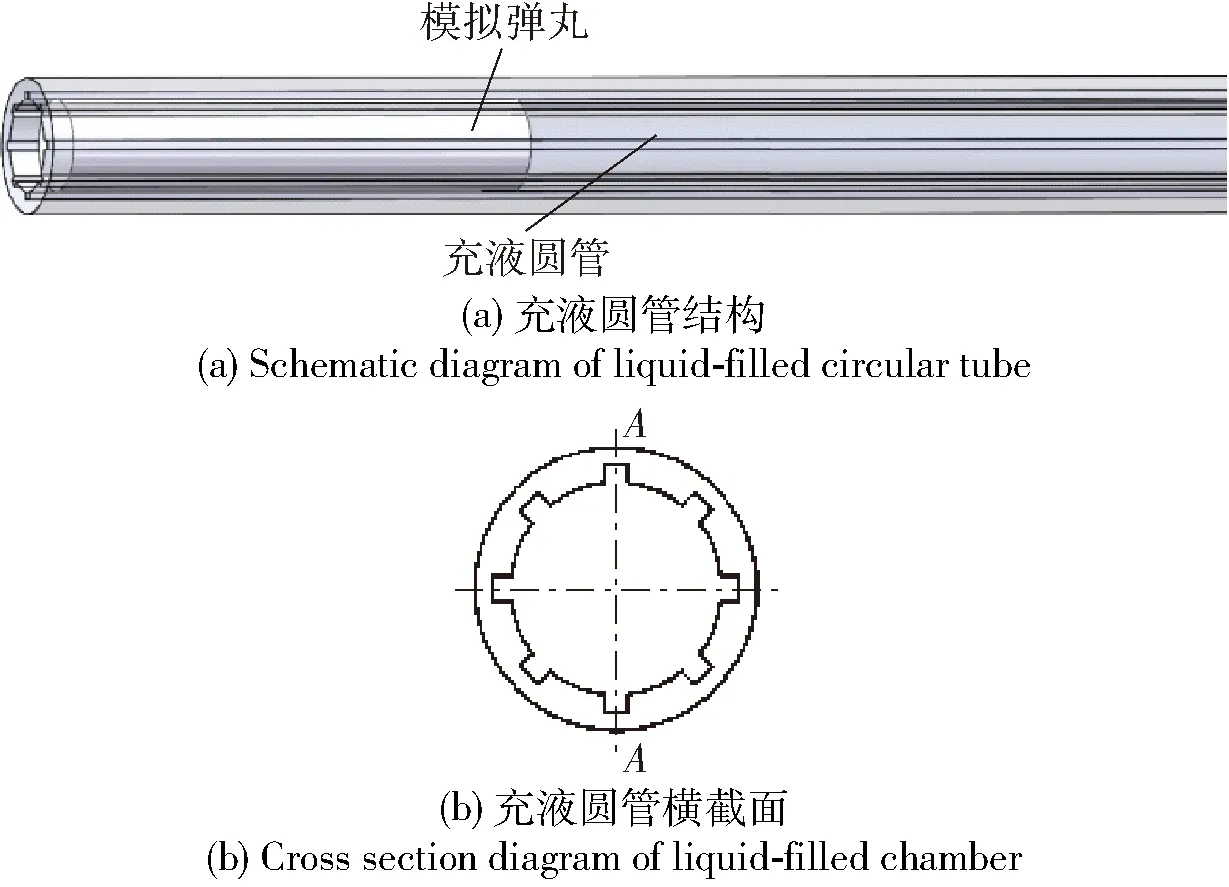
图3 计算模型示意图Fig.3 Cross section of tube

图4所示为计算域及边界条件，计算域的入口压力取10 MPa，入口温度2 200 K，出口条件为大气条件。计算采用基于压力的隐式算法求解，利用PISO算法求解压力- 密度的耦合，利用PRESTO!插值格式对压力项进行离散，为了避免1阶迎风格式可能引起的假扩散问题，密度、动量、能量项的离散采用2阶迎风差分格式。

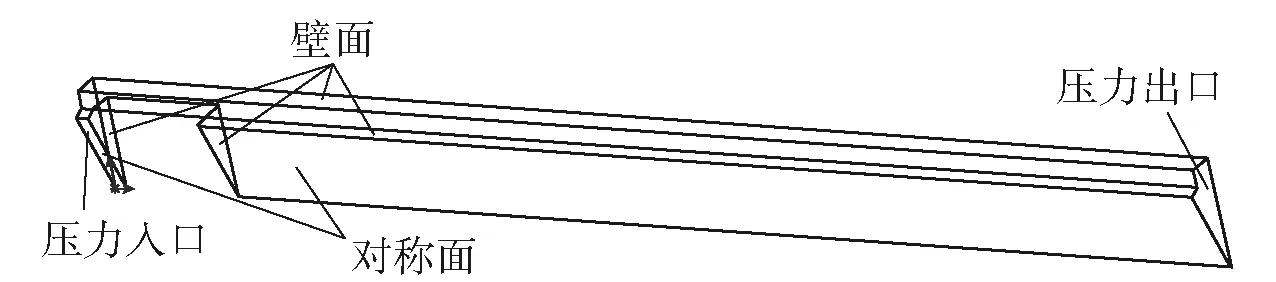
图4 计算区域示意图Fig.4 Schematic diagram of calculational domain

3.2 周向多股壁面燃气射流排水过程分析

图5 充液圆管内燃气扩展过程俯视图Fig.5 Top view of gas expansion process inliquid-filled chamber

为考察周向多股壁面燃气射流扩展及汇聚过程，从充液圆管管口向内观测，得到不同时刻充液圆管内燃气射流扩展过程的俯视图，如图5所示，以燃气射流扩展超过模拟弹丸头部、进入充液圆管内部的时刻为初始时刻t=0 ms. 由图5可见：燃气射流在0.3 ms时开始径向扩展；0.5 ms时开始沿壁面周向扩展，射流的周向扩展滞后于径向扩展；当燃气射流扩展到1.0 ms后，由于相邻凹槽间射流的相互抑制，射流周向扩展速度变慢，射流逐渐脱离壁面；1.9 ms时相邻凹槽间的燃气射流开始相互汇聚，多股燃气射流从独立扩展开始逐渐过渡为联合扩展，射流在不断径向扩展的同时，通过卷吸作用协同排出壁面附近的水；4.1 ms时某一径向截面率先将壁面附近的水完全排出，开始逐渐形成环状气幕；12.7 ms时某一截面上的燃气射流径向完全汇聚，该截面上的水完全排出，气幕基本形成。

为考察周向多股壁面燃气射流的轴向扩展过程，得到燃气射流在充液圆管的对称面A-A面内的组分分布及压力分布随时间的变化过程，如图6所示，x为距模拟弹丸头部的轴向距离，r为距圆管横截面圆心的径向距离。由图6可见：0.1 ms时射流超过模拟弹丸头部进入圆管内部，此时由于弹丸侧壁区域凹槽内的水被燃气不断排出，导致喷孔上方产生了局部高压区；0.3 ms时射流开始产生径向扩展，由于此时进入圆管的燃气量较少，径向扩展会导致射流轴向扩展速度迅速衰减，1.2 ms时射流出现夹断现象；在3.2 ms时可以看到，多股射流间由于卷吸和相互干涉作用，边界湍流掺混愈加明显，表现出了压力振荡现象，射流头部也因此逐渐弯曲靠近；随着多股燃气射流的不断扩展，射流推动水柱向前运动的同时，沿径向相互汇聚，模拟弹丸头部压力逐渐降低，到12.7 ms时燃气射流间已经看不到明显间隙，表明射流之间已基本汇聚，气幕基本形成，此时弹头表面压力降低至1.7 MPa.

图6 射流在对称截面上的气体- 液体组分及压力分布(左为相分布云图，右为压力云图)Fig.6 Phase and pressure distributions of jets in symmertrical section (Left: phase distribution， Right: pressure distribution)

图7所示为射流头部轴向位移及轴向扩展速度曲线。由图7中2条曲线可以看出，燃气射流进入圆管后，轴向扩展过程可以大致分为2个阶段：第1阶段燃气射流刚进入圆管后产生径向扩展，由于此时进入圆管内的燃气量较少，射流的径向扩展抑制了轴向扩展，因此射流的轴向扩展速度不断衰减；第2阶段由于进入圆管内的燃气量不断增加，射流的轴向扩展速度总体上将再次呈上升趋势，但当径向及周向扩展在扩展过程中占主导地位时，射流的轴向扩展速度将短暂地衰减，因此在第2阶段初期，射流轴向扩展速度在波动中逐渐上升，随着圆管内燃气的继续积累，在第2阶段中后期，射流轴向扩展逐渐占据扩展过程中的主导地位，轴向扩展速度的波动逐渐消失，射流轴向扩展速度开始呈非线性上升。

图7 射流头部轴向位移曲线及轴向扩展速度曲线Fig.7 Axial displacement and axial expansion velocity curves of jet head

为了进一步研究圆管内各截面上燃气射流的扩展规律，得到3个径向截面在不同时刻的相分布云图，如图8所示。由图8(a)可见：0.4 ms时射流扩展到x=30 mm截面时，射流头部已由凹槽内向圆管内偏移，随后燃气在该截面逐渐沿径向、周向及凹槽方向扩展，周向扩展明显滞后于径向扩展；0.8 ms时燃气充满该截面的凹槽区域，1.2 ms后该截面的燃气量开始迅速下降，直到1.7 ms时开始再次升高，这是因为在该截面射流出现了夹断现象，到5.7 ms时相邻燃气射流基本汇聚，壁面附近的水由射流的卷吸作用逐渐排出，到10.4 ms时该截面仅有中心区域存在部分液体工质。由图8(b)可见：6.6 ms时射流已扩展到x=230 mm截面，射流头部所在位置与x=30 mm截面几乎一致，表明射流头部没有随射流轴向扩展进一步地沿径向偏移，随后燃气在该截面同样逐渐沿径向、周向及凹槽方向扩展，周向及凹槽方向扩展滞后于径向扩展；7.0 ms时相邻燃气射流间开始汇聚，但此时该截面的凹槽区域内仍存在水，到7.9 ms时该截面凹槽区域内的水被完全排出，此时壁面附近仍存在部分水，直至14.0 ms时壁面附近的水被完全排出。由图8(c)可见：8.6 ms时燃气射流已扩展到x=330 mm截面，9.2 ms时相邻燃气射流开始汇聚，但此时该凹槽区域及壁面附近仍存在水；到11.0 ms时凹槽区域内的水被完全排出，直至16.0 ms时壁面附近的水被完全排出，随后燃气射流继续径向扩展直至汇聚。综合图8(a)、图8(b)、图8(c)可见，多股燃气射流沿轴向扩展的同时，在同一截面上的周向扩展明显滞后于径向扩展，壁面附近与中心区域的水通过卷吸作用逐渐排出，但壁面附近的水先排尽。

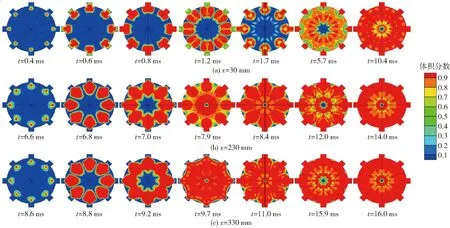
图8 不同时刻相分布云图Fig.8 Phase contours at different moments

图9所示为不同轴向截面燃气面积分数随时间的变化曲线。由图9可见：扩展到x=30 mm的截面时，燃气面积分数迅速上升，1.2 ms时燃气面积分数开始急剧下降，这是因为在该截面射流产生了夹断现象，导致经过该截面的燃气量迅速减小，燃气面积分数急剧下降；随着进入圆管内的燃气量不断增加，该截面的燃气面积分数再次迅速上升，直至该截面被燃气充满。其余各截面燃气面积分数的变化规律具有相似性：当燃气射流刚扩展到某一截面时，该截面燃气面积分数迅速上升，在随后的扩展过程中，该截面的燃气面积分数呈缓慢波动上升的趋势。

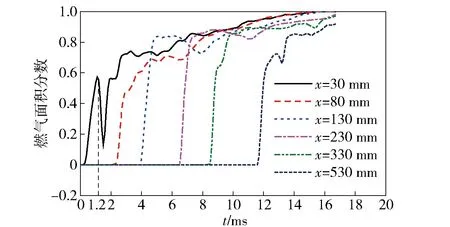
图9 不同轴向截面燃气面积分数变化曲线Fig.9 Curves of gas area fraction of different cross sections

图10所示为充液圆管内燃气体积分数随时间的变化曲线。由图10可见：8股燃气射流向下游扩展，不断推动模拟弹丸前的水排出圆管，使得圆管内燃气体积分数不断增加，排水率不断增大；燃气体积分数呈非线性增长，到15.0 ms时排水率达到86.6%. 由此可见，通过在圆管内壁设计凹槽的方式引导弹后燃气射流向前运动、形成气幕进行排水的效果明显。

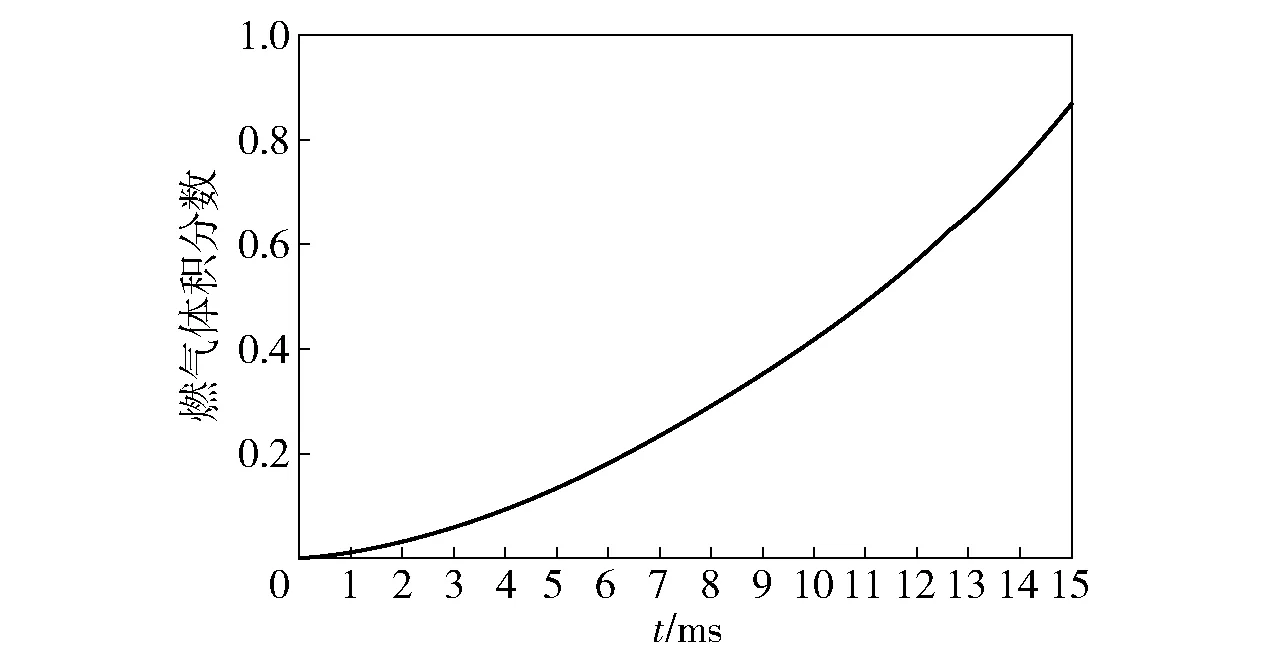
图10 充液圆管内燃气体积分数变化曲线Fig.10 Changing curve of gas volume fraction

4 结论

本文建立了三维非稳态两相流模型，针对30 mm充液圆管周向多股壁面燃气射流的排水过程进行了数值模拟。通过对数值计算结果的分析，得出如下主要结论：

1)燃气射流进入圆管后产生径向及周向扩展，周向扩展滞后于径向扩展；周向扩展沿壁面开始，但在扩展中逐渐脱离壁面。相邻射流在周向完成汇聚后继续沿径向扩展，并开始协同排出壁面附近的水，逐渐形成环状气幕，随后射流继续沿径向扩展，直至完成径向汇聚，形成柱状气幕。

2)充液圆管内，周向多股壁面燃气射流的轴向扩展速度先迅速衰减，随后在波动中缓慢上升，最后波动消失转变为非线性上升。燃气体积分数呈非线性增长，排水效果明显。

3)在喷孔近场区域内，由于强烈的湍流掺混及射流的夹断现象，各截面燃气面积分数在波动中逐渐上升。在喷孔远场区域内，当燃气射流刚扩展到某一截面时，该截面燃气面积分数迅速上升，在随后的扩展过程中，该截面的燃气面积分数呈缓慢波动上升的趋势。