滑模无速度传感器感应电机的简化预测转矩控制

尹华杰 郭志宇 曾君

(华南理工大学 电力学院,广东 广州 510640)

对交流电机来说,磁场定向控制(FOC)和直接转矩控制(DTC)已成为应用最广泛的两种控制方式[1- 2]。近期,模型预测控制(MPC)被认为是替代以上传统控制的一种优良的控制方法。它通过最小化成本函数来选择最佳电压矢量,可以看作最优控制的一种；还可以很容易地考虑各种非线性约束,具有很强的灵活性[3- 6]。

但MPC需要对每个变换器电压矢量的成本函数进行评估,硬件的计算负担很重。减少这种基于枚举的预测方式所带来的高计算负担已成为MPC研究的一个重要问题。文献[7]提出,在所有非零电压矢量中,离误差矢量最近的非零矢量是最优的;通过识别由零电压矢量引起的电流误差矢量的位置,将所需的预测计算数由7减少到1;同时将最佳非零矢量引起的电流误差与零矢量引起的误差矢量做进一步的比较,将二者中产生误差幅度较小的电流误差的电压矢量确定为最终的最佳电压矢量。文献[8]则首先计算下一控制周期结束时消除电流误差的参考电压矢量,并选择与参考电压矢量距离最小的电压矢量作为最佳电压矢量,达到了与传统MPC相同或相似的性能。

MPC的另一个问题是,如果想要控制多个目标,在设计成本函数时通常需要引入权重因子,但在大多数情况下,权重因子难以整定,往往只能通过经验式的试错过程来获得[9],这对许多用户来说不可接受。此外,MPC往往要由速度传感器来提供电机的精确转速,这与交流调速的研究者、生产厂家及用户的共同追求——高可靠性、低成本的无速度传感器控制是不相容的。因此,如果能够实现MPC的无速度传感器化,无疑是极有价值的。

就感应电机的无速度传感控制而言,以往采用模型参考自适应方法的较多[10- 11],它通过构造参考模型和可变模型来估算转速,对干扰较不敏感,但因含有纯积分环节,低速时的观测精度不高[12]。文献[13]构建了卡尔曼滤波器对速度进行观测,但其结构和算法较为复杂。目前,基于滑模理论的速度观测器因结构简单、易于实现、观测精度高、鲁棒性强,正逐渐得到重视[14- 16],已成为无速度传感器研究的热点。

本文针对以上情况,提出了一种基于滑模观测器的无速度传感器感应电机简化模型预测转矩控制策略。它采用多步多目标的控制方式,对系统中的每一个控制目标使用具有单一成本函数的顺序结构,所生成的策略避免了权重因子难以整定的问题;同时,还提出了一种预测计算的简化方法,通过等效变换,将预测转矩中预测电流的计算次数由7减少到1,极大地减少了枚举预测的计算量;最后,设计了一个滑模转速观测器,实现了感应电机MPC的无速度传感器控制效果,并基于Matlab/Simulink的仿真,验证该控制方法的有效性。

1 感应电动机经典MPC的原理

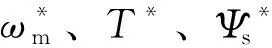
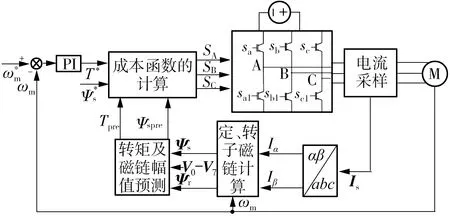
图1 经典MPC控制框图Fig.1 Control block diagram of traditional MPC

图2为两电平逆变器上下桥臂互补导通时8种可能的电压矢量,表1则为它们对应的开关状态SX(上桥臂开通为1，下桥臂开通为0)及α、β分量表示。

IM端口的三相电压瞬时值可表示为

(1)

其中，VDC为逆变器直流侧电压。它们的α-β变换为

(2)

图2 2L-VSI产生的电压矢量Fig.2 Voltage vector generated by 2L-VSI

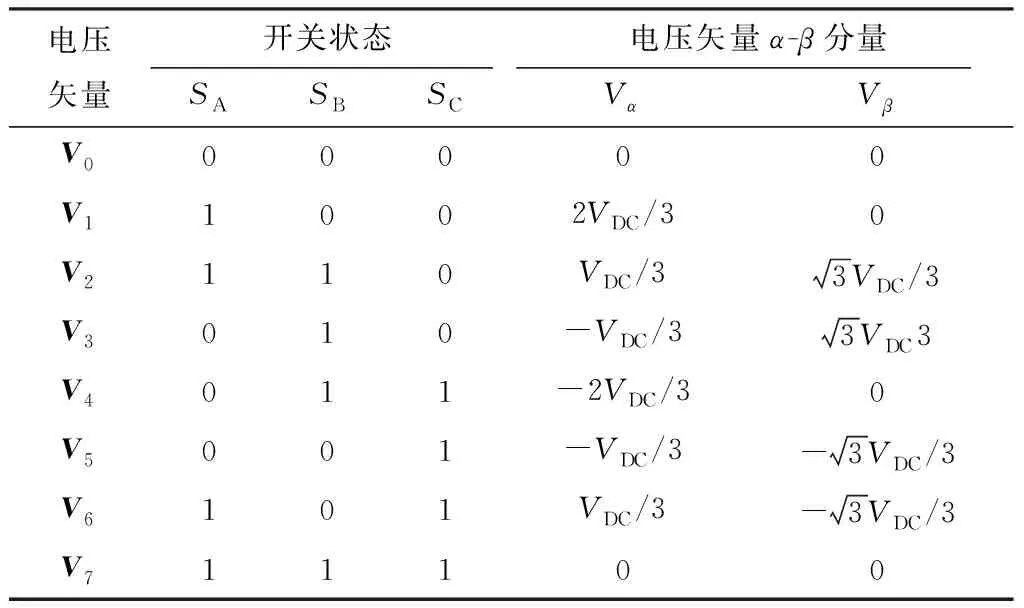
表1 2L-VSI产生的电压矢量及对应的开关状态

选择定子磁链Ψs、定子电流Is为状态变量,则IM在三相静止坐标系下的动态模型为

(3)

(4)

Ψs=LsIs+LmIr

(5)

Ψr=LmIs+LrIr

(6)

(7)

式中:Vs为电压矢量;Ir为转子电流;ω为转子电角速度;p为极对数;Rs为定子电阻;Rr为转子电阻;Lm为互感;Ls为定子电感;Lr为转子电感;T为电磁转矩;TL为负载转矩;J为转动惯量;j为虚数单位。

在MPC控制中,控制器是通过系统模型和k时刻的采样值来预测k+1时刻的系统状态值的。为了得到转矩和磁链幅值的预测值,需要首先计算Ψs、Ψr。

Ψr可根据mt参考系中的等效方程计算,mt坐标系为与转子绕组的磁场轴线对准的旋转坐标系,在mt坐标系中,有:

(8)

式中,tr=Lr/Rr,为转子电磁时间常数。设采样时间为ts,则利用后向欧拉公式,可将式(8)离散为

(9)

利用下式可以计算k时刻的Ψs:

(10)

再对式(3)应用前向欧拉公式,可得Ψs在k+1时刻的预测值:

Ψs(k+1)=Ψs(k)+tsVs(k)-tsRsIs(k)

(11)

对IM而言,定子电流的变化率可以表示为[17]

(12)

同样采用欧拉公式,可以得到定子电流的预测值为

(13)

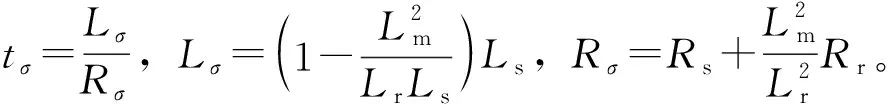
最后,可以得到k+1时刻转矩的预测值为

(14)

在传统MPC中,为了得出每个采样周期内的最优电压矢量,需要构造成本函数,常用的成本函数为[4]

(15)

传统MPC采用枚举法来计算成本函数,即对8个电压矢量依次计算成本函数。控制器在每个采样周期中的动作如下:

步骤1 测量当前时刻的Is(k)、ω(k);

步骤2 根据式(9)、(10)计算当前时刻的Ψr(k)、Ψs(k);

步骤3 选择电压矢量V0,根据式(11)计算k+1时刻的预测值Ψs(k+1);

步骤4 根据式(13)计算k+1时刻的预测值Is(k+1);

热箱室内模拟冬季室内环境，该试验设置温度参数为20 ℃.热箱室内长2.7 m，宽2 m，高2.4 m，外壁为双层彩钢板，中间由150 mm厚聚氨酯发泡塑料构成，其热阻值为4.8 (m2·K)/W，内表面黑度为0.85.热箱热源为电暖器.

步骤5 将步骤3、4中得到的预测值Ψs(k+1)、Is(k+1)代入式(14),得到k+1时刻的转矩预测值T(k+1);

步骤6 根据步骤3和5中得出的预测值Ψs(k+1)、T(k+1),计算式(15)中的成本函数,存储所得结果;

步骤7 将V0依次换为V1-V7,重复步骤3至6,直至获得全部8个电压矢量的成本函数结果;

步骤8 从8个成本函数结果中选择最小值,将对应电压矢量的开关状态应用于两电平逆变器,直至下一采样周期到来。

需要注意的是,上述的测量、数据处理、计算都会带来时间的延迟,因此最优电压矢量的应用必须对延迟进行补偿,通常是增加一个预测步长,即应预测k+2时刻的状态量。这可以很好地解决延迟问题[9]。

2 感应电机MPC的改进及滑模无传感器的实现

2.1 成本函数的改进

对于感应电机,文中选择2个控制目标,即转矩和磁链幅值。首先计算转矩控制的成本函数F1:

F1=|Tpre-Tref|

(16)

对于两电平逆变器的8个电压矢量,F1均会被计算。然后,选取F1最小的两个电压矢量用于下一步中磁通幅值的控制。

F2=||Ψspre|-Ψsref|

(17)

这仅需对上一步选出的两个电压矢量进行计算，然后选取使F2最小的电压矢量应用到两电平逆变器中。可见,改进后的成本函数无需引入权重因子,同时减少了成本函数的计算复杂度。

2.2 基于等效电流的算法改进

从2.1节中的分析可见,在传统MPC的每个采样周期开始时,预测值Ψs(k+1)、Is(k+1)和T(k+1)各要计算8次,尤其是式(13)的Is(k+1)的计算比较繁琐,计算量很大。为此,本文在下面引入一个等效电流来改进MPC,可使每个采样周期只需计算一次等效电流,从而极大地减少计算量。

观察计算预测值Ψs(k+1)、Is(k+1)的式(11)、(13)可见,两式中都有Vs,消去Vs,可得:

(18)

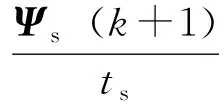
(19)

在转矩预测式中,基于以下矢量恒等式:

a⊗a=0

(20)

(21)

(22)

从而，

(23)

由式(21)可见,等效电流Ise仅与k时刻的定子电流、定转子磁链及角速度有关,而与电压矢量无关,即对于所有电压矢量,Ise均是不变的,因而在每个采样周期中,仅需计算一次Ise,就可以算得所有的转矩预测值,从而极大地减少了计算量。

2.3 基于滑模理论的自适应转速观测器设计

传统上基于MPC的感应电机转矩及磁链控制需要电机的瞬时转速,离不开速度传感器[4]。考虑到速度传感器带来的诸多不便及成本问题[11],文中设计了一个基于滑模理论的自适应速度观测器,以实现感应电机的无速度传感器MPC控制。

在α-β坐标系中,取定子电流、转子磁链为状态变量,并取定子电流为系统输出,可得转子磁链的滑模观测器为

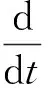
(24)

考虑到矩阵A中参数ω的变化,式(24)的误差等式为

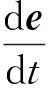
(25)

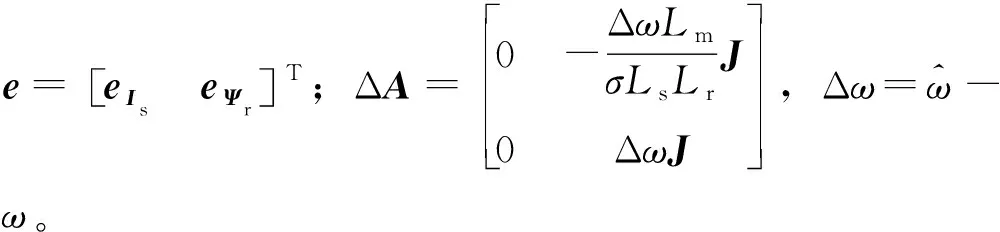
到达滑动模态时,有

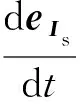
(26)

将式(26)代入式(25),可得:

(27)

式中,G=-K1sgn(s-Is)。当速度为已知参数且不考虑其他参数变化时[18],由式(27)可以得到:

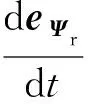
(28)

取Lyapunov函数为

(29)

令V对时间求导,得:

(30)

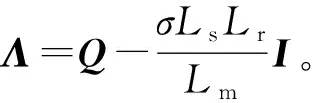
将式(30)的第1项配置为小于0,后两项之和等于0,则可满足Lyapunov稳定性定理[14],此时，

(31)

并可得出转速估计式为

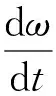
(32)

为提高系统性能,采用如下PI形式的转速自适应收敛律:

(33)

式中，kp为比例系数，ki为积分系数。

此外,由于采用sgn函数时系统的抖振问题比较严重,考虑使用如下的饱和函数代替sgn函数[15]:

(34)

式中，ε为正常数,其取值不能过大,否则会影响系统响应速度。

图3给出了滑模转速观测器的整体框图。

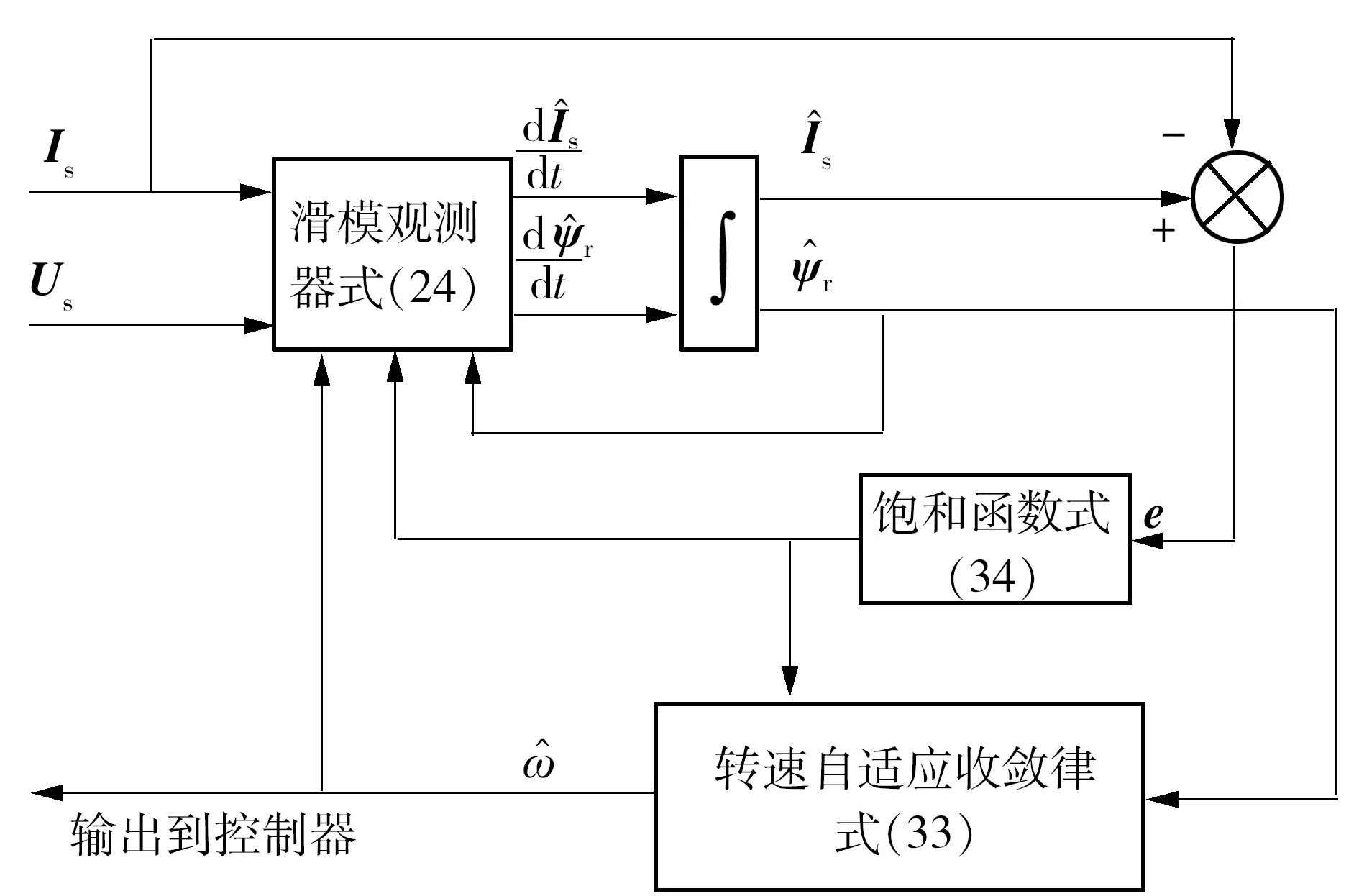
图3 滑模观测器的整体框图Fig.3 Overall block diagram of sliding mode observer

2.4 改善参数误差影响的抑制策略

在本文第1部分的计算过程中,由于感应电机参数的波动性,理论模型与实际系统存在误差,这可能会造成控制性能变差。为了改善这一问题,提高定、转子磁链计算的准确性,可以利用本文2.3节提出的滑模观测器。由图3中可见,本文设计的滑模观测器可以实现对转子磁链的观测。类似地,如果将定子电流和定子磁链设为状态变量,同样可以设计基于定子电流和定子磁链的滑模观测器,实现对定子磁链的观测。使用这两个观测值替换基于理论模型的计算值时,由于本文设计的滑模观测器具有自适应特性,故可以改善参数误差带来的影响。同时,对于定子磁链和转矩的预测值,可以引入反馈校正来提高其准确性[19- 21],具体做法如下。

定义预测误差epre为k时刻预测值与实际值间的误差,则有:

(35)

式中:eTpre、eΨpre分别为转矩及定子磁链在k时刻的预测误差;(k)为k时刻转矩的观测值;s(k)为k时刻定子磁链观测器输出的观测值;Tpre(k)、Ψspre(k)分别为k-1时刻模型输出的预测值。(k)可由k时刻的定子电流实测值及s(k)根据式(14)计算。

由于电机参数变化可以看作是一个缓慢的过程,在相邻两个采样周期内,电机参数可视为常量[22],故可以假设未来时域内的预测偏差与当前时刻相同,即

(36)

从而可以在式(11)、(23)中引入反馈校正:

Ψs(k+1)=Ψs(k)+tsVs(k)-

tsRsIs(k)+eΨpre(k+1)

(37)

(38)

2.5 整体MPC算法流程

采用前述改进的控制策略并引入滑模转速观测器时,MPC控制器每个采样周期的动作如下:

步骤2 由式(35)、(36)计算k+1时刻的转矩及定子磁链的预测误差eTpre(k+1)、eΨpre(k+1);

步骤3 根据式(21)及步骤1的结果计算等效电流Ise;

步骤4 选择电压矢量V0,根据式(37)计算k+1时刻的预测值Ψs(k+1);

步骤5 根据式(38),得出k+1时刻的转矩预测值T(k+1);

步骤6 计算式(16)中的成本函数,存储所得结果;

步骤7 将V0依次换为V1-V7,并重复步骤4至6,直至获得全部8个电压矢量的成本函数结果;

步骤8 从8个成本函数结果中选出最小的两个值,将其对应的电压矢量在步骤4中计算出的磁链预测值代入式(17)中计算成本函数,选择最小的结果,并将对应的电压矢量应用于两电平逆变器,直至下一采样周期到来。

图4给出了相应的控制算法整体框图。

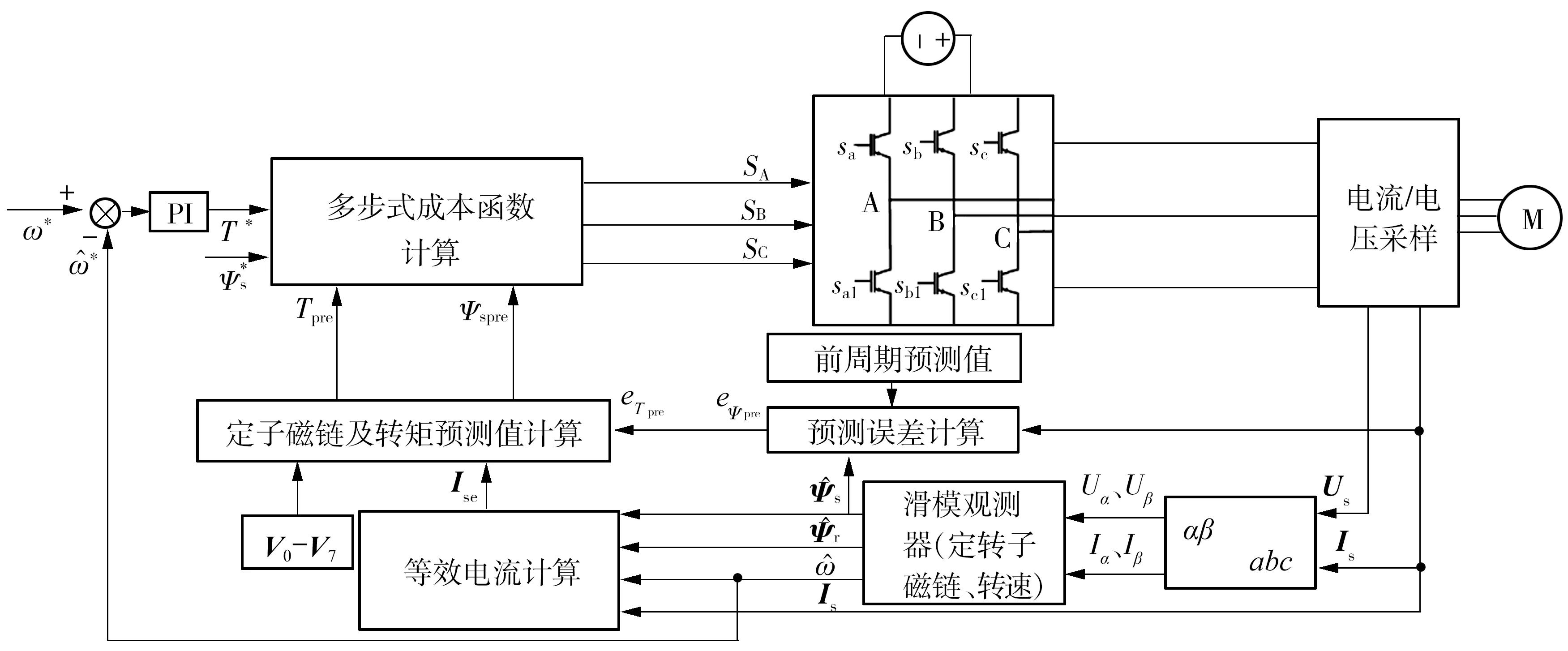
图4 文中所提控制算法的整体框图Fig.4 Overall block diagram of the proposed control algorithm

3 仿真验证

为了验证所提改进的MPC控制及滑模观测器的有效性,并检验其相对传统双闭环矢量控制策略及直接转矩控制策略的优越性[23],针对表2的电机参数,在Matlab/Simulink中对3种策略进行了建模仿真与对比。其中，3种策略均采用了本文所提的速度观测器。

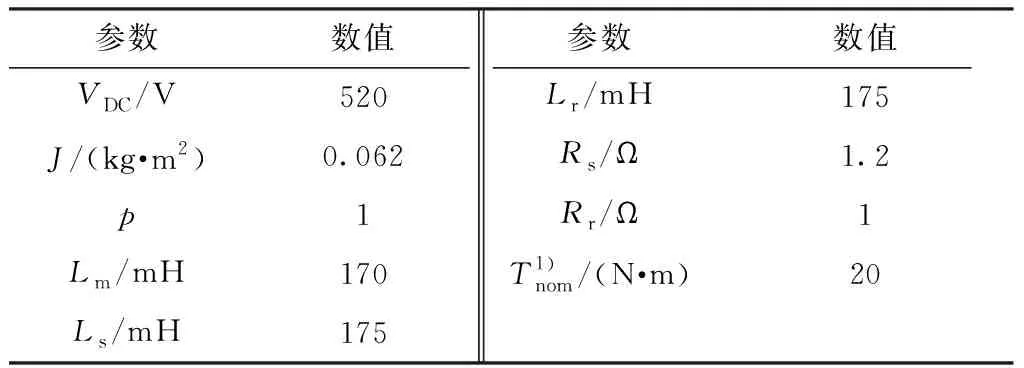
表2 仿真模型的主要参数Table 2 Main parameters of simulation model

1)Tnom为额定转矩。

首先对转速观测器的性能进行验证。图5所示为电机先从0 rad/s加速到150 rad/s,然后再在1.5 s处开始下降到-150 rad/s的过程中,感应电机的实际转速和观测转速,图6则为对应的观测转速和实际转速间的误差曲线。

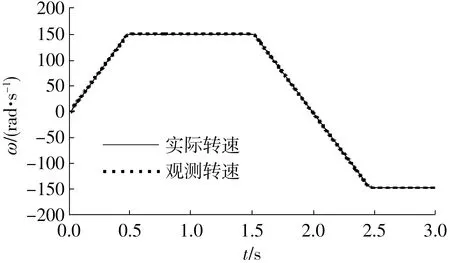
图5 电机的实际转速及观测转速Fig.5 Actual speed and observed speed of IM

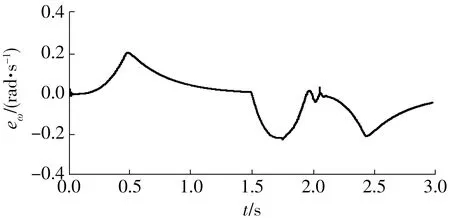
图6 观测转速与实际转速间的误差曲线Fig.6 Error between observed speed and actual speed

由图6可见,观测转速的误差最大值约为0.15 rad/s,且曲线的平滑度很好,这表明该滑模转速观测器具有高精度、低抖动、鲁棒性强的优点。

文中还对系统的稳态及动态性能进行了验证和对比。图7为3种控制方式的输出转矩波形;图8(a)、8(b)分别为稳态和转速参考突变时转矩的动态响应波形放大图;图9为定子A相电流的波形图;图10为定子A相电流在稳态下的放大图;图11为本文所提控制方式的磁链圆图。

可见,在同样采用滑模观测器的情况下,相对于矢量控制及直接转矩控制,本文改进的MPC控制不仅定子电流正弦度好，输出转矩波动小，磁链的幅值波动较小，稳态性能更好,而且转矩的动态响应更迅速、无超调(矢量控制及直接转矩控制的转矩有一定的超调)。

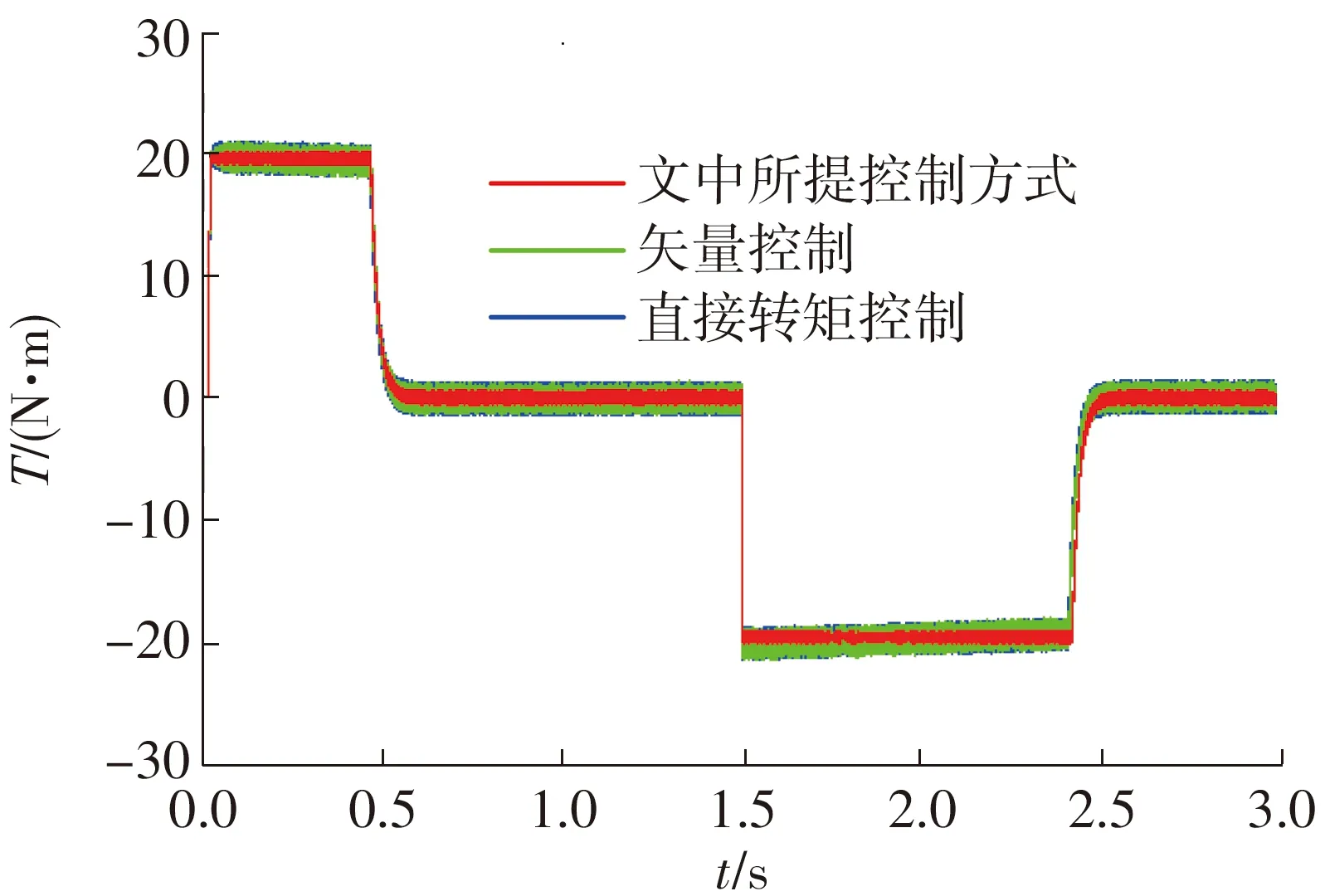
图7 输出转矩波形Fig.7 Waveform of output torque

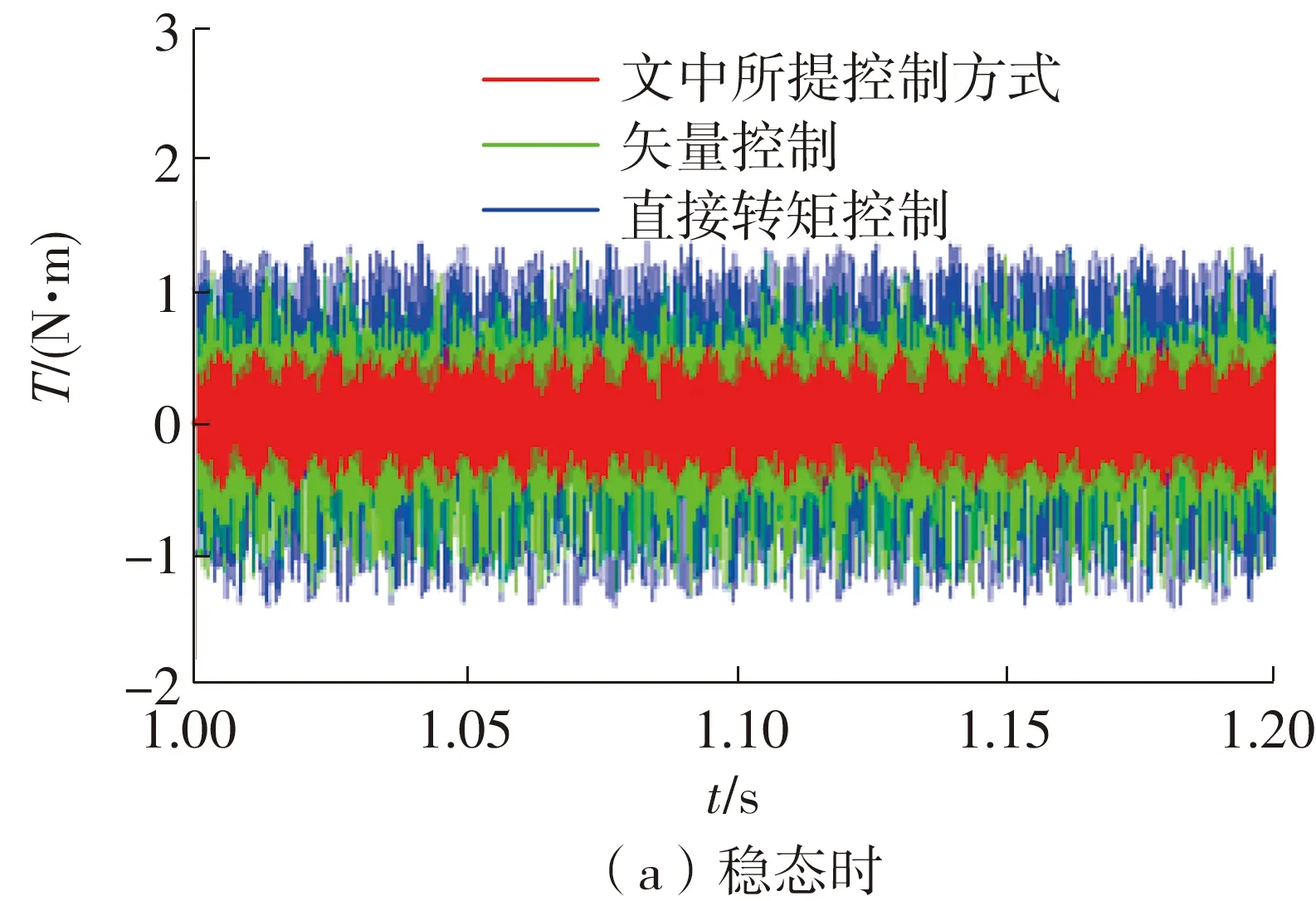
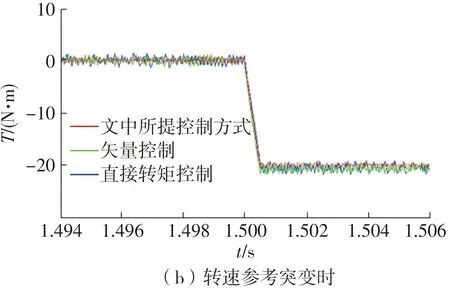
图8 稳态和转速参考突变时转矩的动态响应波形放大图

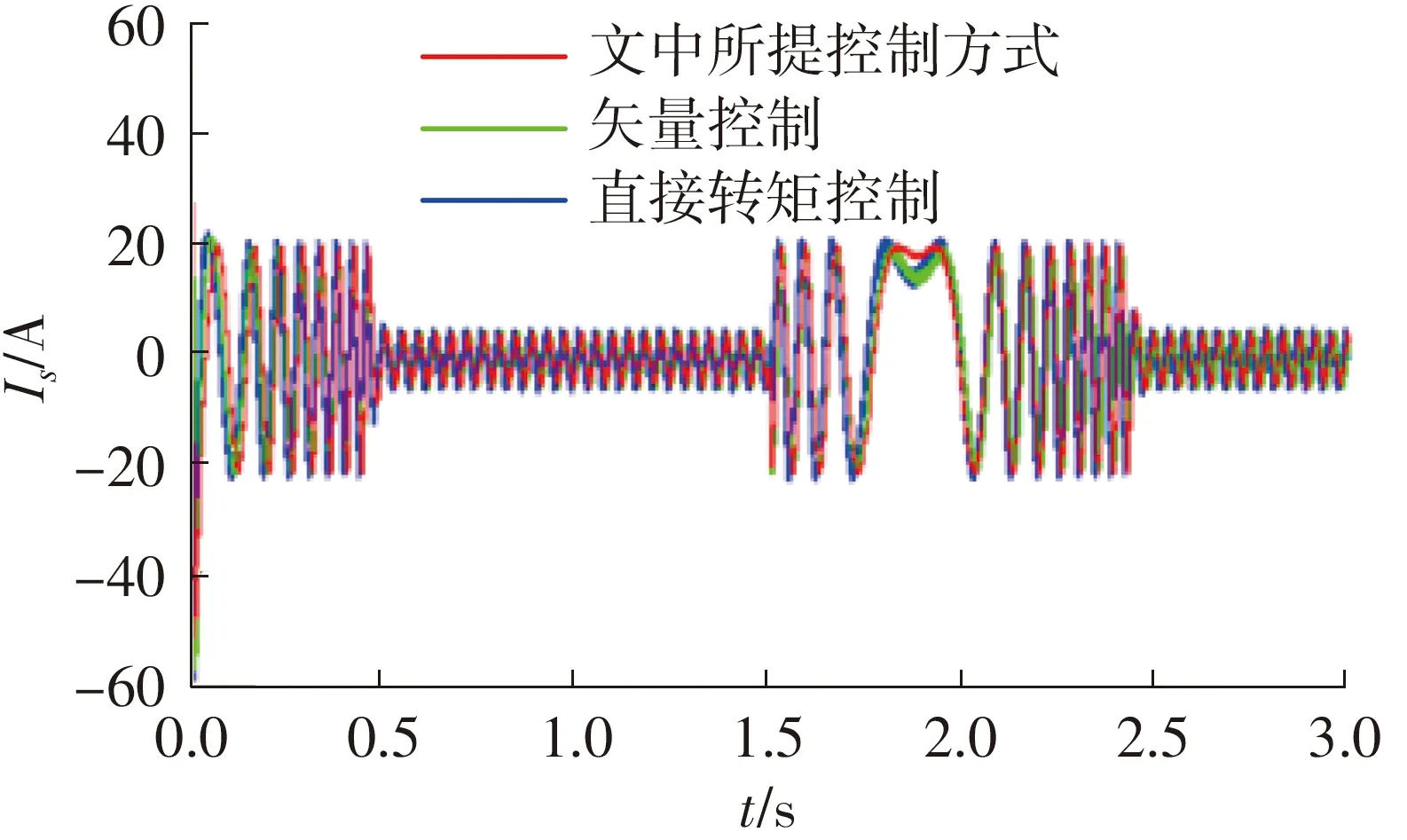
图9 定子A相电流波形Fig.9 Waveform of stator A-phase current

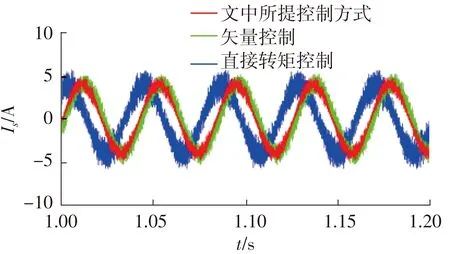
图10 定子A相稳态电流波形放大图

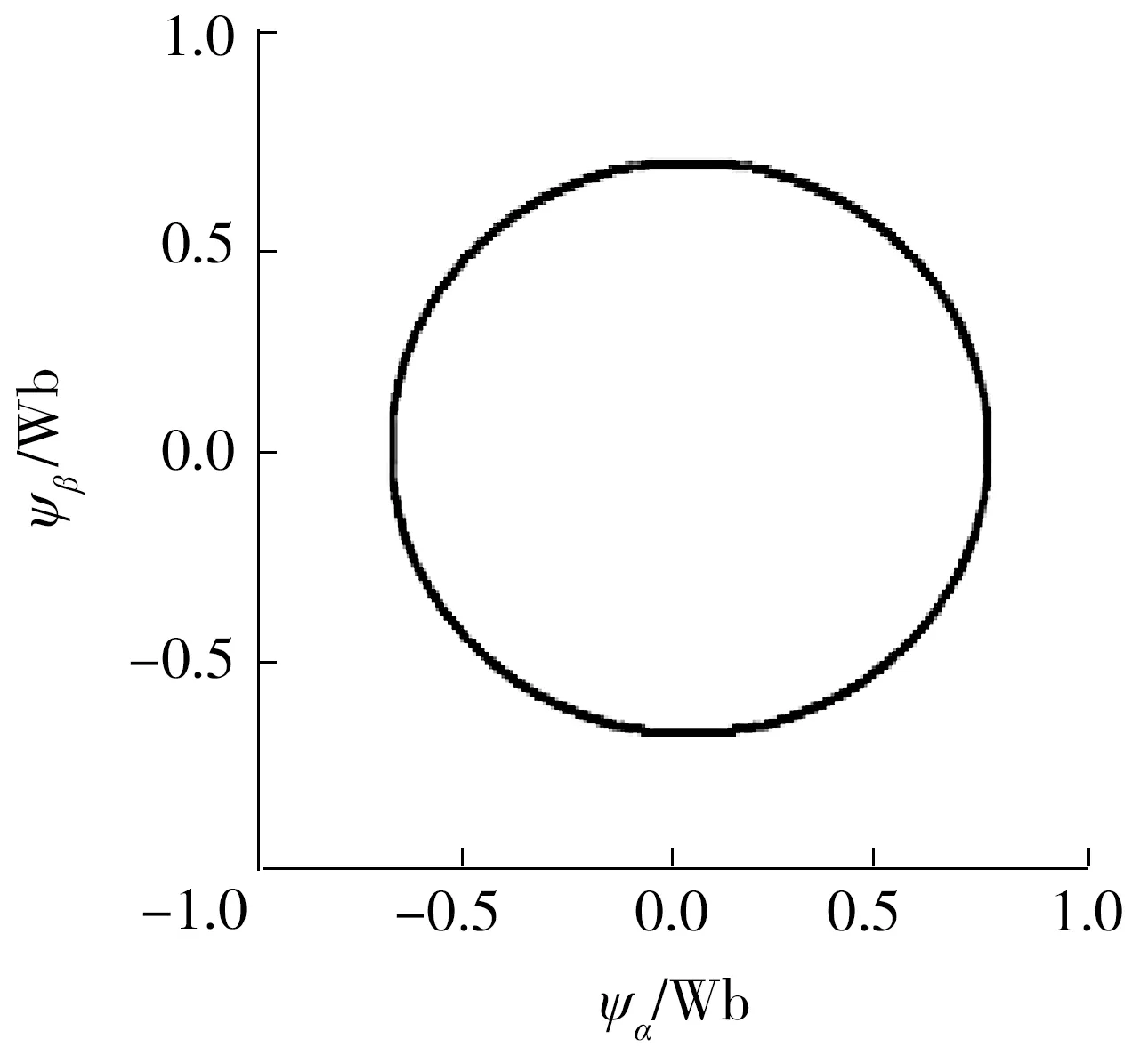
图11 磁链圆图Fig.11 Flux circle

应用过程中,由于本控制策略在计算量上的优势，且无需使用速度传感器,因此在软硬件成本上相比传统的控制策略会有所减少。

4 结论

本文提出了一种两电平逆变器驱动感应电机的改进MPC控制方法。与传统MPC相比,它具有较小的计算量且无需考虑权重因子;又通过引入滑模转速观测器,实现了感应电机的无速度传感器MPC控制,该观测器易于实现且具有优良的性能。通过Matlab/Simulink对比仿真,验证了该控制方法不仅有效且具有达到甚至超过了传统矢量控制、直接转矩控制的静态和动态性能。本文所提控制方法适用于感应电机,考虑到永磁同步电机和无刷直流电机的广泛应用,在进一步的工作中,本文所提控制思想及简化思想同样可用于改良上述两种电机的预测转矩及磁链控制。此外,今后也可探讨滑模增益最优值针对不同电机的求取方法。