基于流体扰动算法与深度神经网络的无人机自适应路径规划

王延祥，王宏伦，吴健发，伦岳斌

（1.北京航空航天大学自动化科学与电气工程学院，北京100191；2.北京航空航天大学飞行器控制一体化技术重点实验室，北京100191）

1 引言

无人机因其具有性价比高、生存性强和可执行高风险任务等优点，在军事和民用领域得到了广泛的发展［1］。在军事应用领域中，无人机已广泛应用于对地攻击、边境巡逻、战术侦察、目标识别等各种军事任务中；在民用领域中，无人机可有效地执行森林火灾检测、资源探测、搜救、航空拍摄、天气预报、测绘等任务。最近30 多年来，随着人工智能技术、计算机技术、控制技术、电子信息等技术的发展，世界各国对无人机领域持续密切关注并加大投入，无人机技术取得了长足的发展和进步，代表了当今高新技术发展的方向。无人机作为一类典型的自主无人控制系统，智能化与自主化是其本质特征与未来趋势。路径实时规划对提高自主飞行能力具有重要作用，而安全避障技术是提高无人机自主飞行能力的关键技术之一。因此，本文对三维复杂动态环境下的无人机实时路径规划技术进行了研究。

本文研究的无人机自主避障问题是指由已知环境信息或传感器（如前视声纳、高频雷达等）实时检测到的环境信息（如障碍物信息等），自主决定无人机的三维避障行为。此外，避障行为应引导无人机由出发点按照一条较优的航路飞向目标点，针对复杂环境下的避障问题，需要考虑环境约束（如各种障碍物、禁飞区、突发威胁等）和无人机运动学约束（如最大转弯速度和最大爬升速率等），使避障问题求解复杂化。在过去的几十年里，经过众多学者们的努力，虽然无人机的自主避障技术取得了丰硕的研究成果，但大多方法都难以在三维复杂动态环境下实时规划出性能指标较优的路径。

现有的这些无人机避障方法主要包括模型预测控制（Model Predictive Control，MPC）方法［2］，快速探索随机树（Rapidly-exploring Random Trees，RRT）方法［3］，人工势场（Artificial Potential Field，APF）法［4］，智能优化算法（如遗传算法［5］、粒子群优化算法［6］）。然而，上述方法主要适用于二维平面，而在三维复杂环境中，计算量将显著增加。此外，生成路径的平滑度也不够理想。

为解决上述避障方法中存在的问题，近年来，受河流中的流水能够顺利避开岩石并最终到达目的地这一自然现象启发，王宏伦等提出了一系列基于流体计算的方法［7-11］，该方法可满足三维复杂环境中的实时路径规划和避障任务需求。其中扰动流体动态系统（Interfered Fluid Dynamical System，IFDS）是最具代表性的方法，该方法具有计算效率高、处理不同形状障碍物、规划路径平滑、适用范围广等诸多优点。需要注意的是，IFDS 有很多参数，这些参数会影响路径的质量。因此寻找合适的参数以生成高质量的路径显得尤为重要，Yao 等［12］提出了基于改进的灰狼优化算法（Grey Wolf Optimizer，GWO）的IFDS 的参数优化方法。但是这种方法只适用于静态已知的环境，而无人机的实际飞行环境通常是动态的、未知的，需要处理各种动态情况。为了提高动态复杂环境中的路径质量，Wu 等［13］根据无人机实时的周围环境信息，采用滚动时域优化控制来不断优化IFDS 参数。然而，这种方法计算量较大，很难保证路径规划的实时性。到目前为止，缺乏对动态环境下参数实时优化的相关研究。

近年来，随着人工智能技术的发展，人工神经网络在路径规划中得到了广泛的应用［14］。基于深度神经网络（Deep Neural Network，DNN）的路径规划存在的难点和重点是如何获取高质量、足数量的训练样本，样本的数量及质量直接影响了路径规划的效率。目前，基于DNN 的路径规划研究还处于探索阶段，研究成果较少。

基于以上分析，在复杂环境下如何根据环境信息实时自适应调整IFDS 参数是一个难题。本文提出了一种基于DNN 和IFDS 的无人机路径规划方法。本文主要由以下三部分组成：（1）基于IFDS 的路径规划模块是基础，（2）基于灰狼优化算法和滚动时域控制（Receding Horizon Control，RHC）的仿真样本生成模块主要用来优化样本质量，（3）基于DNN 的IFDS 系数自适应优化模块是提高路径质量、减少计算开销的关键。

2 无人机避障问题描述

2.1 无人机运动学模型

本文假设无人机装备了稳定的底层控制系统，可以实现对俯仰角、偏航角、滚转角等姿态角以及速度的稳定跟踪或保持。因此可将无人机模型简化为三自由度质点模型，在三维坐标系下的运动学模型如下所示：

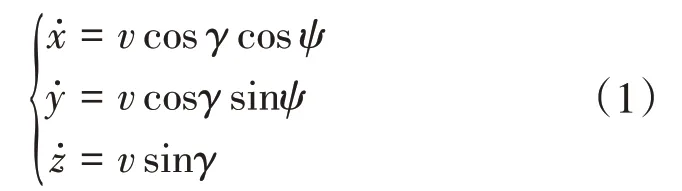
其中，p=（x，y，z）表示在惯性坐标系下无人机的位置，表示无人机速度，v，γ，ψ分别表示无人机的速度大小、爬升角和航向角，γ应满足无人机动力学约束条件γ≤γmax。爬升速率和转弯速率作为无人机的控制输入，其应满足控制输入约束条件。

本文采用比例反馈和前馈控制来确定控制输入：

其中，ψd，γd分别表示期望的航向角和爬升角，这可以通过期望飞行速度vd求得，角速率指令和可以通过差分计算得到。比例因子kψ，kγ分别表示航向角和爬升角时间常数的倒数。令无人机的航向角误差和爬升角误差分别为eψ=ψd-ψ、eγ=γd-γ，通过公式（2）可以推出-kγ·eγ。这说明无人机的航向角误差和爬升角误差均以指数形式衰减到0，无人机的飞行速度v能迅速收敛到期望的飞行速度vd。因此，本文重点研究如何获得期望的飞行速度vd。

2.2 障碍物模型

在复杂的飞行环境中，通常存在许多类型的障碍物，如山峰、建筑物等。这些障碍物可以用圆锥体、圆柱体、长方体、半球体等标准的凸多面体来等效包络，它们可以由统一的公式建模得到：

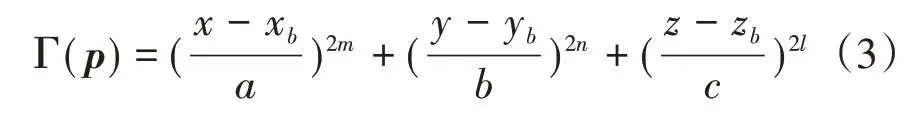
其中，（xb，yb，zb）表示障碍物的中心位置；m，n，l和a，b，c均为大于0 的数，他们决定了障碍物的尺寸和外形。Γ(p) ＜1，Γ(p) = 1，Γ(p) ＞1 分别表示障碍物的内部、表面、外部。在本文中，所有障碍物的内部和表面被定义为禁飞区或危险区：

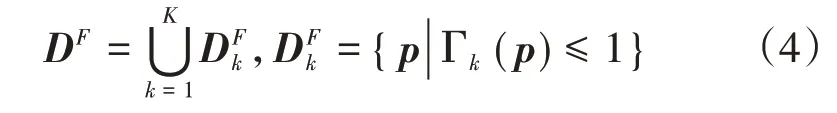
其中K表示障碍物的个数，为了确保飞行安全，无人机在飞行过程中应始终飞行在禁飞区外，即p∉DF。

3 IFDS

受自然界流水避石现象的启发，把河流中的岩石等效替代为无人机飞行环境中的障碍物，当河流中不存在岩石时，流水沿笔直的流线到达目标点，这可以看作为初始流场，初始流线可视为无障碍环境下无人机飞行航路。当河流中存在岩石时，流水可以平滑的绕过岩石到达目标点，这等效为扰动流场，扰动流线可视为障碍物环境下的无人机避障航路。因此，当飞行环境中不存在障碍物时，无人机应从当前位置沿直线飞行至目的地。假设目的地为(xd，yd，zd)，初始期望的流体速度可以定义为：

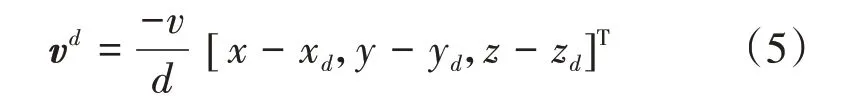
当飞行环境中存在障碍物时，假设障碍物的数量为K。将障碍物对初始流场的影响用总的扰动矩阵M来量化：

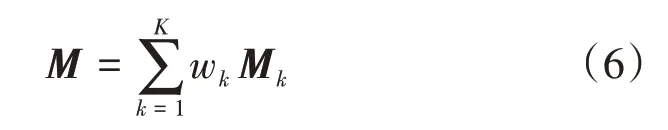
其中wk表示第k个障碍物的权重系数，其值取决于无人机与障碍物表面之间的距离，以及障碍物的尺寸、形状等：

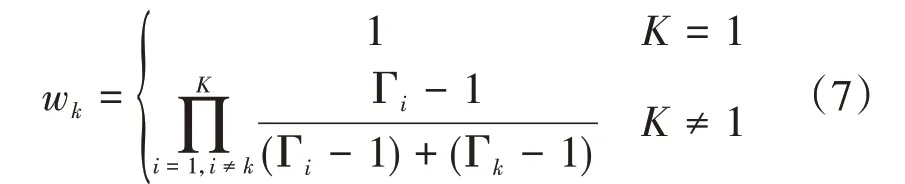
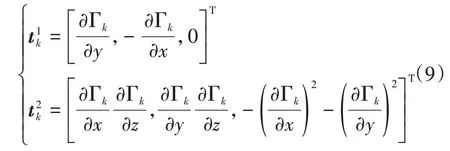
其中θk∈[-π，π]为切向方向系数，表示切向量沿nk（即z′轴）旋转的角度。在惯性坐标系o-xyz中表示为tk，可通过如下公式转换得到：

Rk表示坐标系o′-x′y′z′到o-xyz的坐标转换矩阵。

对于静态障碍物，通过利用扰动矩阵修正初始流场流速即可得到扰动流场流速：

接下来考虑无人机对动态障碍物的规避，首先根据第k个障碍物实际运动速度的预测值uk，obs，定义参考速度：

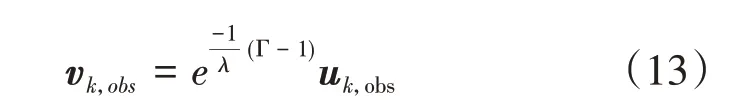
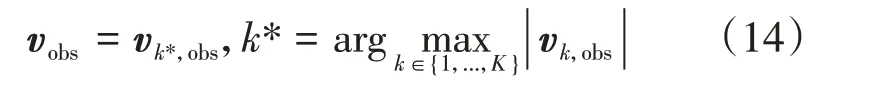
然后，构建相对流场，其中相对初始流场的流速为vd-vobs，相对扰动流场的流速为，因此可以将动态障碍物转换为静态障碍物来处理：

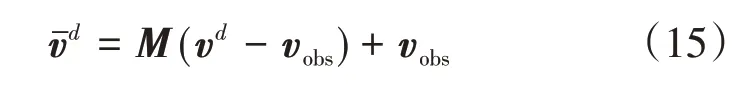
即可得到无人机躲避动态障碍物时的期望飞行速度。

4 基于GWO 和滚动时域优化仿真样本的生成

4.1 GWO

GWO 是一种非常高效的智能优化算法，通过模仿灰狼群的社会等级制度和捕食策略，不断迭代寻找最优值［15］。它具有稳定性好、搜索能力强、收敛性快等优点，已被证明适用于众多工程问题。灰狼是群居动物，有严格的社会等级制度和合作工作，如图1所示，一个种群中的灰狼可以从高到低分为四个等级：首领狼α、副首领狼β、普通狼δ和底层狼ω，且等级越高，个体数量越少。通常等级较低的狼会服从等级较高的狼的命令，有时也会向高等级狼提出建议。为了便于对狼群等级制度进行数学建模，定义群体中历史最优解为首领狼α，次最优解和第三最优解分别为副首领狼β和普通狼δ，所有其他个体为ω。

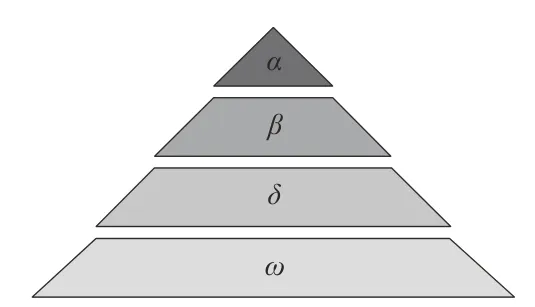
图1 灰狼群体等级制度Fig.1 Grey wolf group hierarchy

灰狼在捕食过程中主要有三个步骤：第一，狼群追踪猎物；第二，狼群包围猎物；第三，狼群逐渐缩小包围范围，接近猎物并将其捕获。假设在D维的搜索空间内，狼群X的个体数量为N，即X=(X1，X2，X3，…，XN)，第i只灰狼的位置定义为Xi=，其中表示第i只灰狼在第d维上的位置。

首先描述灰狼逐渐靠近并包围猎物的行为，第i只灰狼在第d维的位置满足以下公式：

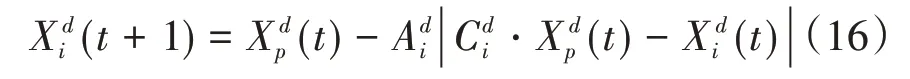
其中t为当前迭代次数，表示猎物在第d维的位置，表示包围步长，定义如下：

其中，rand1，rand2表示［0，1］之间的随机数，变量a随迭代次数的增加从最大值amax递减到最小值amin：

其中tmax表示最大迭代次数。

灰狼在围捕猎物时往往知道猎物的位置Xp（即实际参数优化问题中的最优解），但在实际参数优化过程中，猎物位置Xp是未知的。通常情况下，灰狼α、β、δ能更好地反应猎物的潜在位置，因此灰狼群体可以根据α、β、δ的位置Xα、Xβ、Xδ进行搜索：

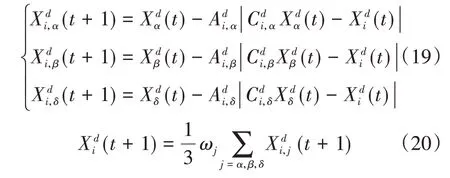
其中，ωj(j=α，β，δ)表示α、β、δ的权重系数：

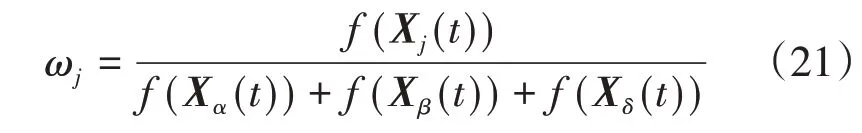
其中f(Xj(t))表示第j只狼在t时刻的适应度值，在本文中f为规划的路径长度。

4.2 滚动时域优化

基于DNN 的自适应优化效果在很大程度上取决于样本的质量和数量。对于无人机在军事航空方面的应用：在样本数量方面，获取足够数量的真实飞行样本需要付出较高的代价；在样本质量方面，难以保证无人机飞行的路径每一步都是最优的。本文通过仿真生成训练样本的方式解决以上难题，算法流程如图2所示。首先，在区域S={(x，y，z)|0＜x＜5000 m，0＜y＜5000 m，0＜z＜1500 m}内随机产生20 个大小、形状各不相同的障碍物，随机选择不同的位置作为无人机路径规划的初始位置和目标点。然后，使用IFDS 来规划避障航路，在规划的每一步中，均采用GWO 寻找基于当前相对位置、速度及航向的IFDS 的最佳参数，通过寻找合适的参数使剩余路径规划成功且长度最短。之后，更新IFDS 的参数并前进一步，再继续基于当前状态调用GWO 优化和更新IFDS 参数。该策略也可以看作是一种特殊的滚动时域控制，时域长度是从当前位置到路径规划结束。

5 IFDS系数自适应优化

虽然采用智能优化算法可使规划路径全局最优，但该方法优化产生的系数是始终不变的，无法根据环境的变化做出相应的调整，且计算量较大，因此该方法仅适用于静态已知的环境。滚动时域优化可用于动态环境下的局部优化，但通常情况下该算法耗时较长，难以保证路径规划的实时性。针对以上问题，本文引入DNN 基于当前环境实时自适应调整IFDS 参数。以ψ、d_min 和φ作为DNN 的输入，其中ψ表示无人机当前航向，d_min表示无人机与障碍物的最近距离，φ表示无人机指向目标点的矢量和无人机到最近障碍物的矢量之间的夹角；IFDS 的排斥系数ρ、切向系数σ、方向系数θ作为网络输出端的特征提取。通过经验数据和不断尝试将隐藏层神经元数目设为6，隐藏层设为3 层，并选择Sigmoid函数作为激活函数，最大迭代次数设为5000。采用DNN和带冲量的梯度下降算法，以均方差为损失函数，通过离线训练的方式以消除训练时间对实时路径规划的影响。为测试训练所得网络的泛化性能，随机选取20%的样本作为测试集，经测试均方根误差为0.00241，说明训练所得网络具有较强的泛化能力。该方法的总体框架如图3所示。

6 仿真验证

为验证本文提出的基于DNN 和IFDS 的实时路径规划方法的高效性，在Matlab 2018b 中进行了仿真验证。仿真参数如下：采样周期ΔT设为0.5 s；无人机速度v=20 m/s；最大转弯速率最大爬升速率；最大爬升角γmax=π/6；控制器增益设为kψ= 0.1，kγ= 0.1。

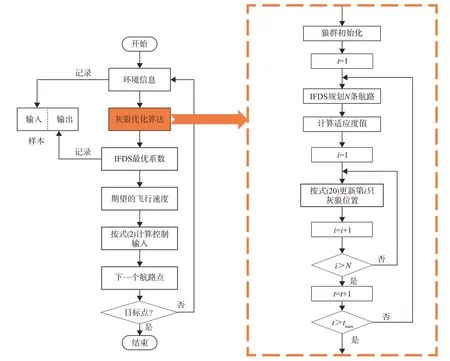
图2 仿真样本生成框架Fig.2 The framework of simulation sample generation

图3 整体系统架构Fig.3 The structure of the overall system

6.1 躲避静态障碍物

为证明该方法的鲁棒性，随机选取六个不同位置作为无人机航路规划的起始点和目标点。如图4所示，路径1 中，无人机初始位置为（0，0，400）m，目的地为（5000，5000，500）m，初始航向角为π/2，初始爬升角为0；路径2 中，无人机初始位置为（0，1000，200）m，目标点为（5000，25000，300）m，初始航向角和初始爬升角都设为0；路径3 中，无人机初始位置为（2000，0，300）m，目标点为（3500，5000，400）m，初始航向角为π，初始爬升角为0。仿真结果表明，针对不同的飞行环境，本文提出的方法所规划的航路均可安全到达目标点。该方法的优点是可以根据周围环境实时自适应的调整参数，具有较强的鲁棒性，而经典方法根据经验手动调整参数可能会因参数不合适而导致路径规划失败。

为了进一步分析本文方法所规划的路径性能指标，以路径1 为案例，将本方法规划的路径与GWO 优化的全局最优路径进行比较，如图5所示。全局最优路径长度为7590 m，本文方法规划的路径长度为7660 m，可见其规划效果接近于全局最优解。

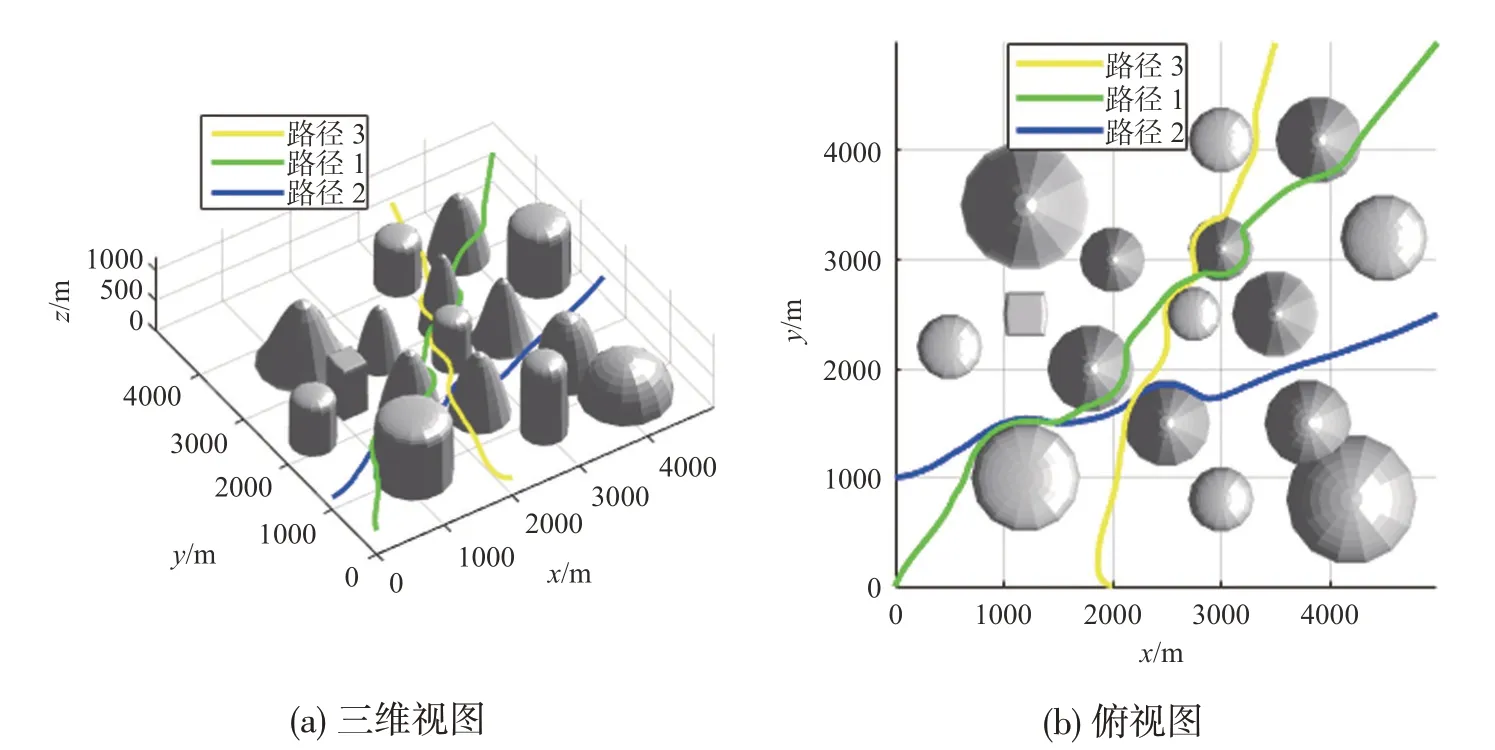
图4 本文方法路径规划结果Fig.4 The paths planned by the proposed method

图5 本文方法与全局最优路径对比Fig.5 The proposed method is compared with the global optimal path

6.2 躲避动态障碍物

假设无人机从（0，0，400）m 处出发，向终点（5000，5000，500）m 处飞行，初始航向角为π/2，爬升角为0。在任务空间中，存在两个运动威胁：圆柱形威胁半径200 m，初始位置为（200，1800，0）m，运动方程为vx=9+0.01t，vy=20cos（0.03π·t）-0.03t，vz=0；椭球形威胁半径为200 m，初始位置为（800，3500，500）m，运动方程为vx=8+0.02t，vy=-8+0.03t，vz=0。关于移动威胁的运动信息可用扩展卡尔曼滤波（EKF）在线估计得到［16］。动态威胁轨迹及无人机航路规划效果如图6所示，无人机与动态威胁表面之间的距离如图7所示，无人机与动态威胁表面的最短距离均大于0，这表明无人机能够成功地避开动态威胁到达目标点。经统计，该方法的单步规划平均耗时为0.0131 s，远远小于采样周期，而传统的滚动时域优化方法平均耗时为0.4532 s，说明本文所提出的方法计算开销小，实时性强，能够完成复杂动态环境下的路径规划任务。

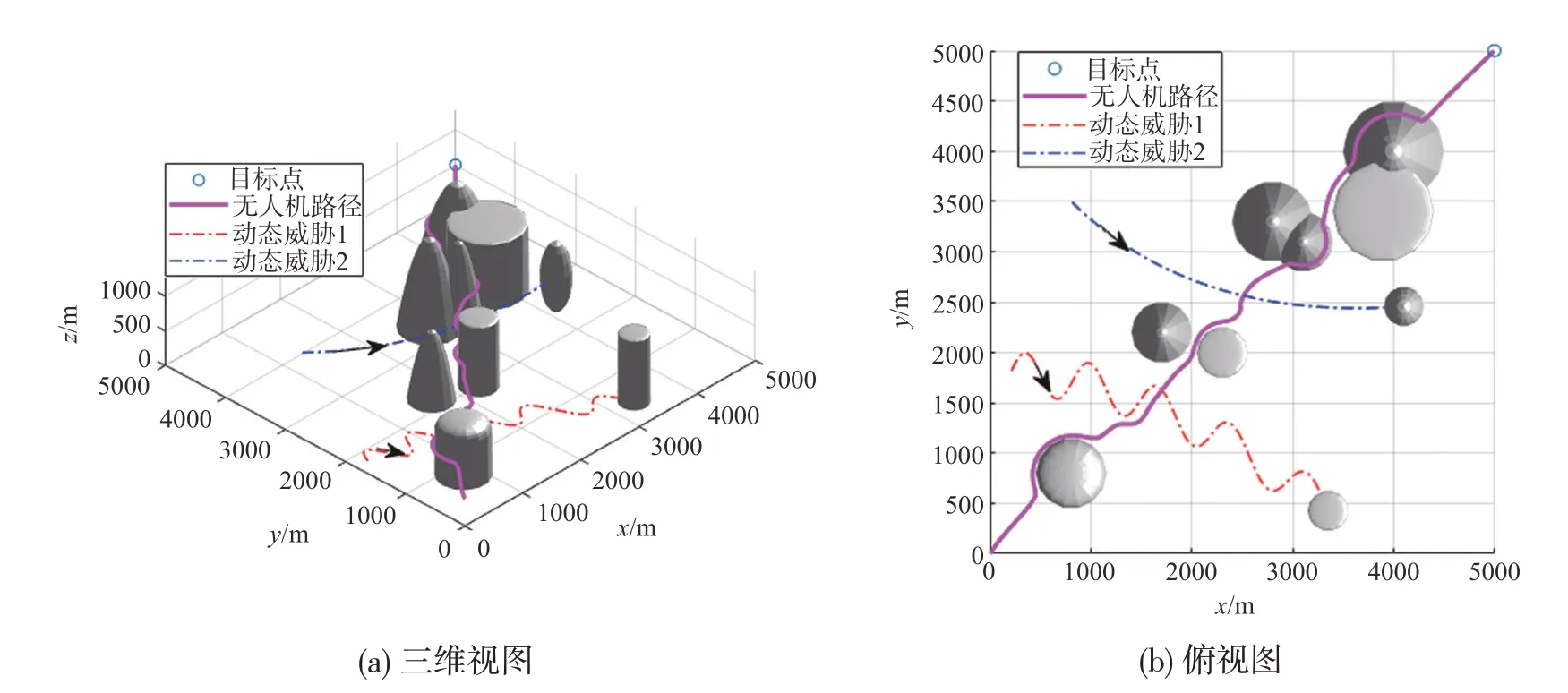
图6 无人机躲避动态障碍物Fig.6 UAV avoids dynamic obstacles

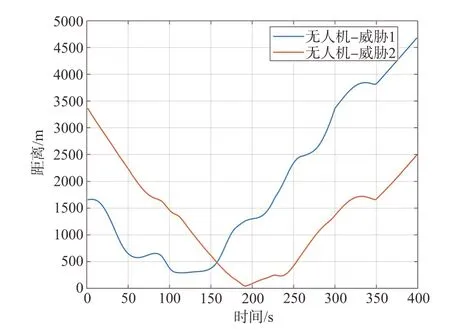
图7 无人机与动态威胁表面的距离Fig.7 The distance between the UAV and the dynamic threat surface

7 结论

本文针对三维复杂动态环境下无人机的路径规划问题，首次将DNN 强大的自适应学习能力和IFDS高效的避障效率有效地结合起来，以满足各种任务的要求。经仿真验证结果表明，该方法具有较高的鲁棒性，较强的实时性，同时规划的航路具有较好的性能指标。主要结论如下：

（1）基于GWO 和滚动时域优化来生成仿真样本，有效地解决了DNN 训练样本质量不高和数量不足的难题。

（2）引入离线训练好的DNN来根据当前时刻无人机所面对的环境信息自适应调整IFDS 系数，解决了难以选取合适系数的问题，提高了避障效率。

（3）本文提出的方法在保证路径质量的前提下，同时适用于静态环境和动态环境。有效解决了智能优化算法只适用于静态环境，而动态环境下的滚动时域优化计算开销较大的问题。