基于模块化神经网络的船舶航迹航速预测

王文标, 董贵平, 汪思源, 田志远, 杜佳璐

(大连海事大学船舶电气工程学院， 大连 116026)

随着云监控技术以及传感器技术的不断进步，船舶的物理信息、运动信息及航迹行为信息等大量信息被存储，这些信息被广泛应用在船舶异常行为检测、提高船舶监控效率及预防航行事故。对船舶航迹进行预测研究，预测船舶在未来时刻的航速与航迹等行为信息，对加强海上交通监管和预防海上航行事故发生具有重要意义。

目前，传统的船舶航行行为预测方法有：卡尔曼滤波算法[1-3]、灰色模型[4]、支持向量机[5]、马尔科夫模型[6]等，其中支持向量机在有限样本情况下能得出较高的预测精度但在大数据量问题中的表现欠佳；其他方法都需要建立船舶运动学方程，而多变的海况条件一定程度上加大了模型的复杂度，影响模型的预测精度。随着神经网络的不断发展，更多的学者倾向于使用神经网络预测船舶航行行为[7-10]。但是，上述算法均采用单一全互连神经网络预测模型，随着船舶预测问题难度的增加，高维输入和大数据量等复杂问题影响着神经网络的最终结构，过大或较小的网络结构都会影响网络的预测精度。

为使神经网络结构更加简洁并进一步提升船舶航迹预测精度，现引入脑功能分区模块化设计理念(分而治之)搭建神经网络船舶航迹航速预测模型，首先，使用归一化互信息与专家知识将船舶航行行为预测任务分解为航速与航迹两个独立的子任务；其次，将子任务传输到Elman子网络与PSO-RBF子网络中学习；最后，将学习结果集成，从而完成船舶航迹航速的预测。

1 基本概念

1.1 模块神经网络构架

如图1所示，模块化神经网络旨在模拟人脑功能分区的模块化架构，由多个子网络组成，各子网络分别学习总任务中的相应独立子任务,旨在模拟大脑“分而治之”的方法来提高神经网络处理复杂任务的综合性能[11-14]。

图1 模块化神经网络系统结构图Fig.1 Structure diagram of modular neural network system

1.1.1 任务分解

将一个难以学习的任务分解成多个容易学习的子任务是实现 “分而治之” 的前提，文中运用归一化互信息分析所获取的船舶数据中待选输入变量与预测变量间的非线性关系，计算出与预测变量相关性较大的输入变量；然后, 基于专家知识删除掉与预测变量无关或相关性较低的输入变量, 最终确定输入变量的选取，完成任务的分解。

1.1.2 子网络

子网络的学习能力诠释了整个神经网络的性能，子网络对子任务的学习就相当于整个神经网络对任务进行训练的过程。在实际应用中,子网络的建模精度和建模速度是受到重点关注的两大优化目标。

1.1.3 输出整合

MNN采用组合学习模式，分为子网络学习与集成模块学习。其输出模块对各子网络的集成公式为

(1)

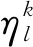
(2)

1.2 归一化互信息

互信息能够验证变量间是否存在关系以及关系的强弱的一种信息度量方式。设X={x1,x2,…,xk}，则X的熵为

(3)

式(3)中：p(xk)为xk的概率密度。对于两个变量(X,Y),联合熵公式为

(4)

式(4)中：p(xk,yl)为xk和yl的联合概率密度函数。互信息用熵与联合熵的关系可表示为

I(X,Y)=H(X)+H(Y)-H(X,Y)

(5)

原始样本数据间数量级差别较大易引起预测误差，对数据的原始样本进行归一化处理是模型预测的前提。归一化互信息(normalized mutual information，NMI)是将互信息缩放到[0,1]，不但抵消了不同量纲和取值范围的影响，还保留了原始样本间存在的关系。其公式为

NMI(X,Y)=2I(X,Y)/[H(X)+H(Y)]

(6)

2 子网络设计

子网络选用对历史状态数据敏感的Elman神经网络训练和预测船舶航迹。同时，因为RBF神经网络较强的非线性映射能力，可用于训练和预测船舶航速[15]。

2.1 PSO-RBF子网络

RBF神经网络共为3层，如图2所示。设其网络结构为s-m-n(s为输入层节点数、m为隐含层节点数、n为输出层节点数)，则第v个输出节点的输出为

(7)

(8)

式(8)中:δi为激活函数的扩展宽度[13]。文中使用减法聚类算法与误差反馈相结合的方法确定隐含层神经元个数，所构建的 RBF神经网络能以紧凑的结构获取较好的非线性映射能力。

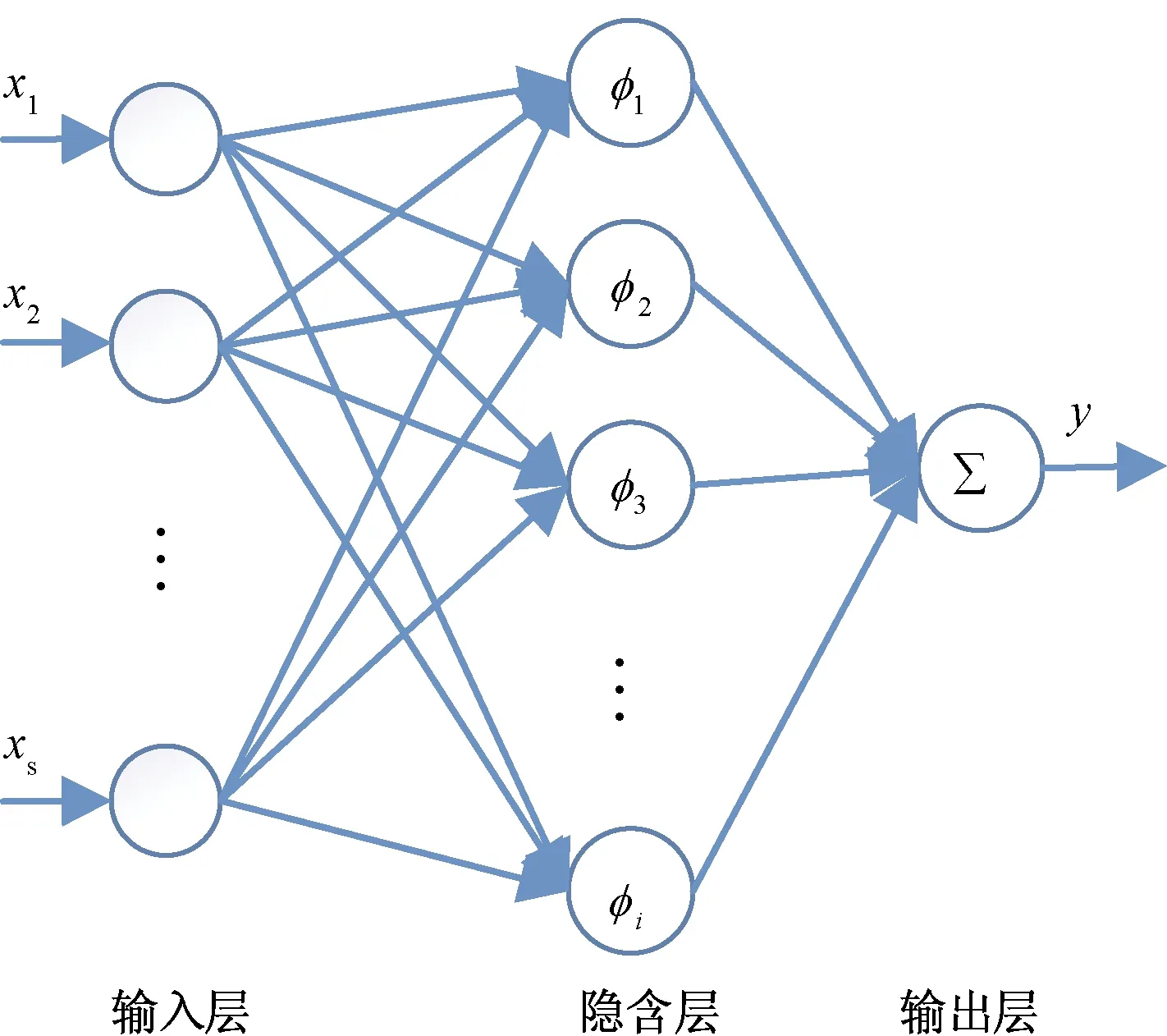
图2 RBF神经网络结构Fig.2 Neural network structure of RBF

2.1.1 粒子群优化算法

粒子群优化算法是近年来发展起来的一种算法，该算法具有结构简单、精度高、收敛速度快、全局搜索能力强等优点[16]。

在粒子群优化算法中，每个粒子都代表问题的一个可能的解决方案。粒子的共同特征表现为位置、速度和适应度值。每个粒子通过寻找适应度极值来更新自身的位置和速度。适应度极值主要包括个体极值Pbest和全局极值Gbest。通过适应度函数可以计算出粒子的适应度值，从而判断粒子的优劣。在发现Pbest和Gbest后，PSO确定了每个粒子的速度和距离。

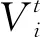
(9)

式(9)中：ω称为惯性因子；C1和C2为加速常数；R1和R2一般取[0,1]上的随机数。文中主要通过PSO算法优化RBF网络隐含层的学习参数，这样能够提高RBF网络的预测性能。

2.1.2 减法聚类算法与误差反馈确定隐含层神经元

首先通过减法聚类算法确定隐含层初始神经元个数。通过减法聚类思想计算每个样本数据的密度值De，计算公式为

(10)

式(10)中:ra为聚类半径；Xi与Xj为q维空间中的p个数据点。为避免在已有聚类中心相邻点出现新的聚类中心，通过式(11)对数据点密度进行修正：

(11)

式(11)中:Dem为第m个数据点的密度指标；rb为一个密度指数函数显著降低的邻域。为防止相似距离的聚类中心出现，一般选择rb=1.5ra。

初始神经元确定后通过训练集样本中的最大误差来判断隐含层增加神经元的依据。设ep为第p个样本的当前网络输出误差，其中yp为网络预测值，op为网络实际值，p=1,2,…,P，P为训练样本个数，计算公式为

ep=yp-op

(12)

由此得到误差向量e=[e1,e2,e3,…,ep]T,确定最大误差所在位置为

emax=max(e)

(13)

pmax=Index(emax)

(14)

式中：emax为误差向量中最大值，当第p个样本所对应的实际输出与预测输出误差最大且最大误差大于平均误差, 则认为网络对第p个样本的学习不充分。因此新增一个 RBF 神经元对当前样本重新学习,平均误差公式为

(15)

当emax≤emean或达到期望训练精度时，则认为网络构建完成。新神经元增加后其扩展宽度进行如下改变：

δm=0.2min[dist(cm,cp≠m)]

(16)

当最大误差小于平均误差或达到期望训练精度时，则认为网络构建完成。

2.2 Elman子网络设计

Elman神经网络拥有一层传统神经网络(back propagation,BP)不具备的承接层，如图3所示，通过承接层将上一时刻输出返回到隐含层使其具有记忆功能[18]。这种构造使得Elman神经网络在处理动态信息、预测时间序列等问题时，相较于传统BP神经网络更为容易。因此，选取其对船舶航迹进行建模。其数学表达式为

y(t)=g(ω3x(t))

(17)

x(t)=f[ω1u(t)+ω2x(t-1)]

(18)

u(t)=x(t-1)

(19)

式中：y、x、u分别为输出层、输入层、承接层向量；ω1、ω2、ω3分别为各层间的权值；f()为隐含层传递函数；g()为输出层传递函数。

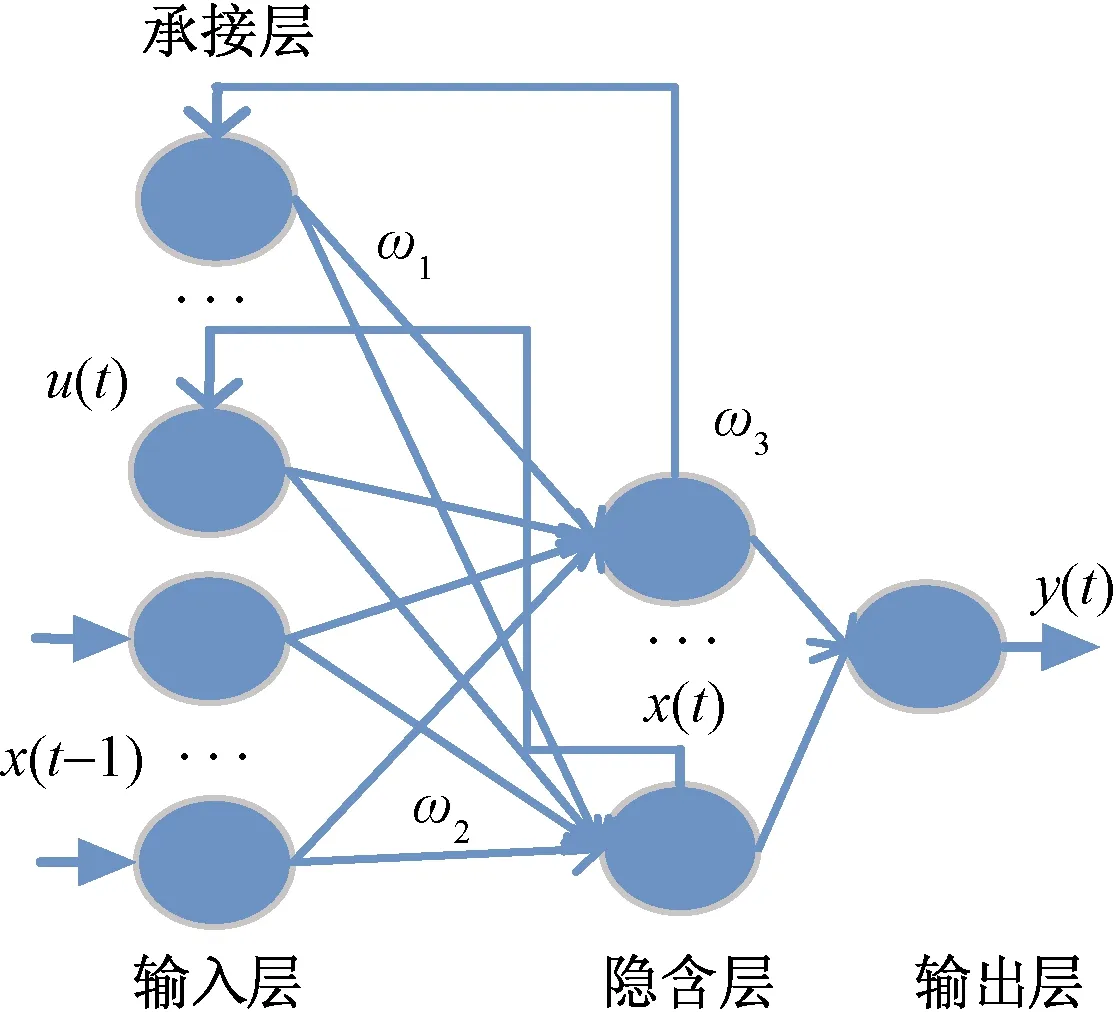
图3 Elman神经网络结构Fig.3 Neural network structure of Elman

2.2.1 动态增长型Elman神经网络设计

Elman神经网络隐含层神经元个数的选取影响着网络的性能，神经元太多或太少都会影响网络的性能，如何选取隐含层神经元个数仍然是一个尚待解决的问题。使用减法聚类算法确定隐含层初始神经元个数，在此基础上通过判断训练精度是否满足性能函数来动态增加隐含层神经元个数。

设t时刻网络的误差为e(t)，其公式为

ep(t)=yp(t)-op(t)

(20)

式(20)中：yp(t)为t时刻网络预测值；op(t)为t时刻网络实际值；p为输出神经元个数，p=1。

网络性能函数选取均方误差，公式为

(21)

神经元δ动态增长公式为

(22)

式(22)中：γ为一个极小的正数；Fix()为取整函数。如式(22)所示，随着MSE的动态变化，神经元δ的个数也在动态增加。

3 预测结果与分析

将平均绝对误差(mean absolute error,MAE)与均方根误差(root mean squared error,RMSE)作为网络精度的评价标准，其公式为

(23)

(24)

式中：Y(i)为预测值；y(i)为实际值。

使用大连海事大学“育鲲轮”训练船真实数据集，“育鲲轮”船长116 m，船宽18 m，MMSI号为412701000，呼号为BQHZ；选取航速10～15 kn(1 kn=1.852 km/h)的数据，并要求数据发送间隔为10 s，以此保证船舶航行动态时间序列数据的等时间间隔要求。

通过归一化互信息与专家知识选取航速、航向、船舶位置(经度、纬度)与船舶吃水作为输入变量；选取230组数作为建模数据并做归一化，前200组用于网络训练，30组用于网络预测。图4为航速预测结果，图5为航速预测误差。航速训练过程中神经元数增长情况如图6所示，初始的6个神经元为减法聚类算法计算的结果，在此基础上，基于误差反馈的自增长方法将网络神经元数目最终确定为8个。

图4 航速预测结果Fig.4 Speed prediction results

如表1所示，模块化神经网络的航速最小预测误差为0.007 1 kn，最大误差为0.085 5 kn，RMSE值为0.001 7，MAE值为0.030 1；BP神经网络的航速最小预测误差为0.052 9 kn，最大误差为0.122 3 kn，RMSE值为0.005 7，MAE值为0.072 4；RBF神经网络的航速最小预测误差为0.005 0 kn，最大误差为0.119 6 kn，RMSE值为0.004 8，MAE值为0.064 9。

图7为航迹预测结果，图8为经度与纬度的预测误差，图9为经度与纬度训练过程中神经元的增长情况，与航速预测神经元增长情况有所不同的是，航速预测神经元为+1增长，航迹预测神经元则根据式(22)动态增长。

图5 航速预测误差Fig.5 Error of speed prediction

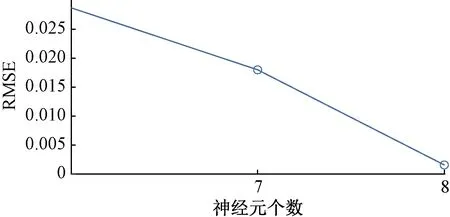
图6 航速训练过程神经元增长曲线Fig.6 Neuron growth curve during speed training

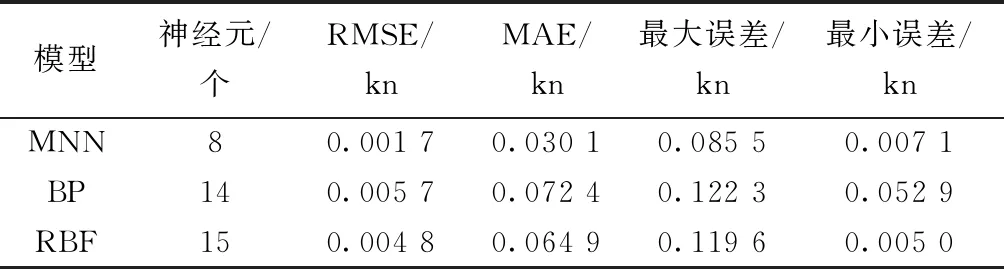
表1 航速预测结果对比

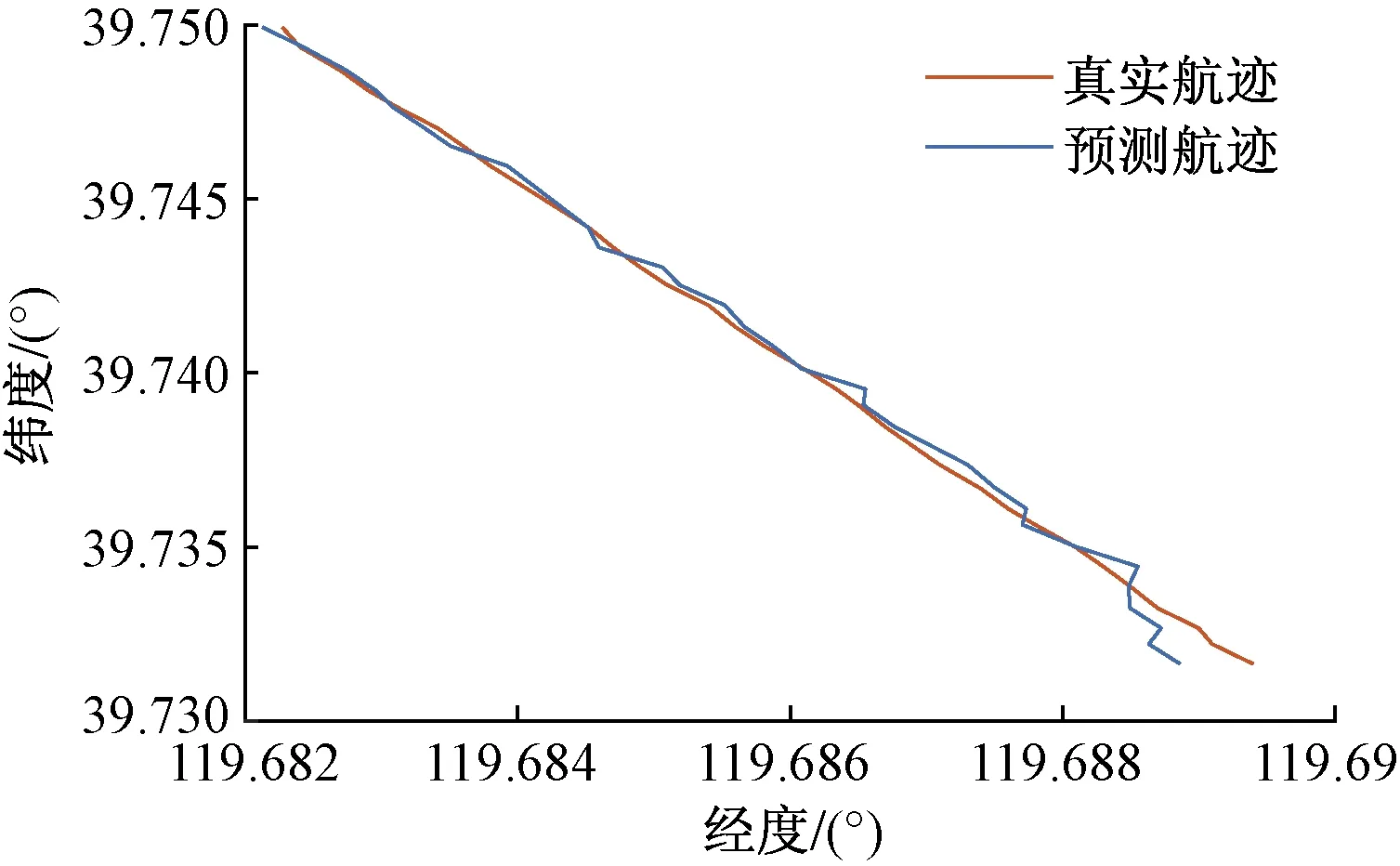
图7 航迹预测结果Fig.7 Track prediction results

如表2所示,模块化神经网络的航迹预测隐含层神经元个数较少且网络性能最好，全互连BP神经网络与全互连RBF神经网络性能达到与MNN神经网络相似精度所需的神经元个数较多，网络结构较为冗余。

图8 航迹预测误差Fig.8 Track prediction error

图9 航迹训练过程神经元增长曲线Fig.9 Neuron growth curve during track training

表2 航迹预测结果对比

综合对比MNN、BP与RBF三种神经网络的预测结果与隐含层神经元个数，MNN网络结构更加紧凑，综合性能优于BP与RBF神经网络，验证了本文方法的预测精确性。

4 结论

为获得更高精度的船舶航行行为预测结果，借鉴模块化神经网络“分而治之”这一设计理念完成了对航迹与航速的同步、准确预测并得出以下结论。

(1)使用船舶真实数据进行预测模型对比实验，在预测精度上，MNN比全互连RBF神经网络与全互连BP神经网络准确性更高。

(2)在神经网络网络结构上，MNN的网络结构更加简洁。