兼顾军用飞机使用的跑道快滑位置优化模型

陈奇奇， 王观虎， 李 柯

(空军工程大学航空工程学院， 西安 710038)

随着民用航空的高速发展，民用机场建设进入新阶段。抓住民用机场建设的机遇期，在现有民用机场改扩建及新建机场规划过程中，适时地提出相应国防标准并加以落实，为民用机场平战时军用飞机的使用、军事作战能力的提升奠定坚实的基础，这对于提高军队作战效率、多样化作战部署具有重大意义[1]。目前中国越来越重视民用机场的平战结合功能，但受到多种因素和条件制约，致使贯彻国防标准的工作并没有很好开展起来。而出现这种情况最重要的原因之一是相关技术标准规范欠缺。并没有对军、民用机场的标准及差异性进行过系统的研究，对民用机场真正应预留的相应设施功能还没有探讨过。快速出口滑行道(简称快滑)是连接跑道与滑行道的一条通道，飞机着陆滑跑过程中，达到快滑允许的转出速度即可从快滑驶出，而不必从端联络道驶出。这样既可以减少飞机的滑跑距离，降低航油的消耗，还能减少飞机占用跑道时间，提高机场的运行效率[2]。为了充分发挥快滑的作用，选择合适的快滑位置至关重要。在设计快滑位置时，同时要考虑兼顾军用飞机的使用，否则待建成投入使用后，若不满足军用飞机的使用需求，会严重降低军用飞机的运行效率，造成重大后果。

近年来，中外学者对军用机场与民用机场的跑道快滑位置进行了大量研究[3-5]。陆松等[6]基于可靠性理论，以加权无效着陆滑跑距离为目标函数构建了快滑位置优化模型，确定了军用机场快滑最优位置。种小雷等[7]针对多机型共用的快速出口，提出综合利用率的概念，确定了军用机场快滑最优位置。李明捷等[8]将民用飞机着陆过程分为三个阶段，运用三阶段法确定每种机型最佳转出距离，并引入机型运行比例确定民用机场快滑最优位置。Benlic等[9]以最小加权跑道占用时间为目标函数，提出了启发式搜索算法，并以曼彻斯特机场为例设计了快滑位置。Cem等[10]对快速出口滑行道的平面尺寸进行了研究，通过分析不同飞机的性能，确定不同快滑出口角度下所允许的最大转出速度。

上述研究从不同角度分析了军用机场与民用机场的最优快滑位置，有一定的参考和借鉴意义。但目前对于兼顾军用飞机使用的民用机场快滑位置研究还缺乏系统性，现通过分析民用飞机与军用飞机着陆过程的异同，以及着陆过程影响因素的分布规律，使用蒙特卡洛方法模拟飞机着陆过程，计算飞机着陆转出的最佳位置。通过构建以最小加权无效占用跑道时间为目标函数的快滑转出位置模型，基于动态规划思想，设计模型求解程序。最后以腾冲机场为例进行实例分析，兼顾军用飞机的使用，确定快速出口滑行道的最优位置。研究结果为未来军用飞机使用民用机场奠定基础，为民用机场预留军事功能提供技术支撑。

1 飞机着陆影响因素及转出距离分析

1.1 军民用飞机着陆过程

军用飞机在下滑着陆时，发动机处于慢车工作状态，当下滑至高度8～12 m时，开始放下起落架并对准跑道T字布进行接地。通常情况下要求飞机接地点在T字布正侧方，但受到各种因素的综合影响，有时飞机会提前接地，有时会延缓接地，一般着陆接地点都在T字布附近。飞机接地后进行刹车滑跑，此过程一般视作匀减速运动，当飞机减速滑跑到快滑位置且速度满足出口要求时，可直接从快滑出口驶出。若此时飞机速度不满足快滑驶出速度要求，则需要继续滑行一段时间从端联络道滑出，飞机在跑道上的着陆距离为

Ll=l+Sl

(1)

式(1)中：Ll为飞机从着陆到驶出跑道所需的跑道长度；l为飞机着陆接地点到跑道后端的距离；Sl为飞机着陆滑跑距离。

其着陆滑跑过程如图1所示。

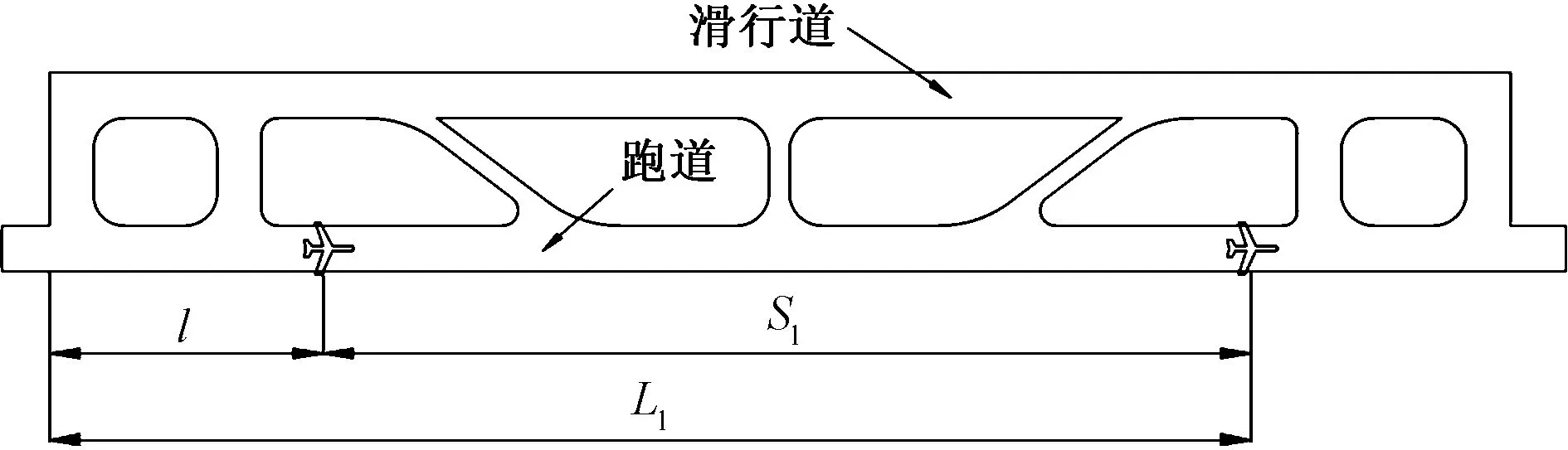
图1 飞机着陆过程示意图Fig.1 Schematic diagram of the aircraft landing process

民用飞机着陆过程与军用飞机类似，飞机从进场高度(标准为15 m)按照固定角度下降，当快接近地面时，调整飞机与地面的角度，拉平飞机，直到飞机主起落架接地。之后迅速将发动机调到反推，打开减速板，飞机进行减速滑跑，直至达到安全转出速度离开跑道。

1.2 着陆影响因素及其规律

根据文献[11]，可得到飞机着陆滑跑距离计算公式为

(2)

(3)

式中：ml0、vl0为标准大气条件下的飞机着陆质量与接地速度；ml为飞机实际着陆质量；Δ为空气相对密度；p为实际气压；t为实际气温；vw为分解到跑道上的风速，顺风为正，逆风为负；μl为综合阻力系数；Pm为慢车推力；i为平均坡度，顺坡着陆取负，逆坡着陆取正；Kl为着陆滑跑驾驶误差系数。

当飞机以快滑出口允许的最大速度vex转出时，在跑道上所需要的着陆滑跑距离为

(4)

式(4)中：vex为快滑出口所允许的最大转出速度。

式(4)已经给出了影响飞机着陆距离的因素，在上述公式中，其中一部分影响因素只与飞机的型号、机场环境有关，在飞机每次飞行中变化不大，可视为常量。而另一部分在飞机每次飞行中有较大变化，应视为随机变量，下面对这些因素进行分析。

1.2.1 着陆接地点到跑道端的距离

(1)军用飞机。

军用飞机下滑着陆时在目测点将飞机拉平后，须在T字布正侧方的跑道上接地。但在实际着陆时受到多方面因素影响，着陆距离会发生较大变化。根据部分学者[12]通过对飞机着陆性能以及对大量着陆数据的拟合研究，发现l3大致服从正态分布，且多在T字布附近。并且飞机相对于地面的着陆速度同样会影响到接地点的距离，着陆速度大小的变化直接导致接地距离的变化，着陆速度变化越大，接地点的分布则越不均匀。T字布通常设置在距跑道端200 m处，因此l可表示为

l～N(200,σ2)

(5)

其概率密度函数为

(6)

为便于计算，将其转化为服从标准正态分布，有

(7)

设显著性水平为α，置信度为(1-α)，则置信区间为

(8)

飞机着陆时距离T字布两侧的最远距离即为l3的置信区间，将飞机从平飘到接地这一短暂过程中的速度视为恒定，假设对接地点分布的影响时间为Δt，则可得到着陆速度和接地点分布关系式：

(9)

(10)

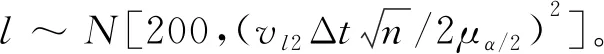
(2)民用飞机。

根据国际民航组织的实地调查及部分学者[8]的研究分析，对于某一特定机型，飞机着陆接地点至跑道入口的距离可视为常数，根据机型不同，一般在250～450 m。但当跑道受到风速影响或纵坡影响，需要对该距离进行修正，其具体修正值如表1所示。由表1可知，每存在0.25%的下坡，A、B类飞机滑跑距离延长30 m，C、D类飞机则延长50 m，每存在0.25%的上坡，A、B类飞机滑跑距离缩短30 m，C、D类飞机则缩短50 m。对于下坡跑道，驾驶员在着陆进行观察时，常会感觉跑道变缓，导致错后接地。而对于上坡跑道，会给驾驶员很陡的错觉，导致提前接地。对于风速修正同理，不再一一赘述。

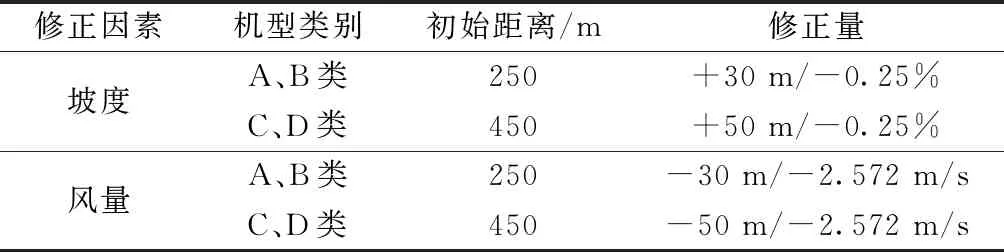
表1 着陆接地点至跑道端距离及修正方法

1.2.2 气温气压

由式(3)可知，空气相对密度由气压与气温所决定，机场的气温与气压在一天中是相互影响、实时变化的，同时气压的高低不仅受温度影响，还受气流的影响，规律较为复杂。因此为简化计算，取机场所在海拔的平均气压，视为常数。关于气温变化规律，大致服从正弦分布，公式为

(11)

式(11)中：tmax为一天中最高气温；tmin为一天中最低气温；sin(ΔT)为一天内温度的正弦变化规律。

1.2.3 风速

风速影响飞机着陆方式的选择，目前无论是军用机场还是民用机场都会选择逆风降落，即当分解到跑道上的顺风风速较大时，飞机可从另一端进行逆风着陆，减小着陆滑跑距离。根据部分学者[13]对跑道风速的大量统计与实际调查研究，发现分解到跑道方向上的风速服从指数分布，公式为

(12)

E(vw)=1/λD(vw)=1/λ2

(13)

1.2.4 驾驶误差系数

实际测量飞机起飞或着陆的滑跑距离与按标准驾驶动作理论计算的滑跑距离的比值即为驾驶误差系数，公式为

(14)

式(14)中：S为实测着陆滑跑距离；S0为按标准驾驶动作理论计算的着陆滑跑距离；K为驾驶误差系数。

1.2.5 驶出速度

根据出口滑行道与跑道的夹角不同，飞机的驶出速度会发生变化。对于出口滑行道，出口角度一般为直角，如图2所示。对于快速出口滑行道，出口角度一般为锐角。《民用机场飞行区技术标准》(MH 5001—2013)规定[14]，出口角度一般介于25°～45°，如图3所示，建议取30°，而30°跑道快滑出口所对应的飞机驶出速度不大于25.83 m/s。但在飞机实际运行中，会受到侧风或地面摩阻力等不利因素的影响，驶出速度往往较小，因此考虑各种不利因素，为保证行驶安全，对驶出速度做一定修正[6]，如表2所示。

图2 直角出口滑行道Fig.2 Right angle exit taxiway

图3 快速出口滑行道Fig.3 Fast exit taxiway

表2 不同角度的转弯速度

图4 仿真逻辑框图Fig.4 Simulation logic diagram

1.2.6 着陆质量、慢车推力及跑道纵坡等因素

着陆质量、慢车推力、跑道纵坡和平均阻力系数在某一飞机每次飞行中，变化不大，因此可视作常数。

1.3 着陆转出距离计算

结合实际问题，利用蒙特卡洛方法[15]计算飞机着陆最佳转出距离。由于军用飞机和民用飞机在着陆接地点至跑道端距离计算方法略有差异，因此为提高计算结果的精确率，更贴近实际值，军、民用飞机最佳转出距离应分开计算，其仿真逻辑框图如图4所示。

2 快滑转出位置优化模型

2.1 模型构建

假设共有R类飞机使用跑道，候选出口总数为N。为了得到快滑最优设计位置，兼顾军用飞机的使用，以最小加权无效占用跑道时间为目标函数，建立快滑位置优化模型：

(15)

式(16)～式(22)为其限制条件：

(16)

式(16)表示各个机型的占比之和应为1。

Dk+1-Dk≥Dmin

(17)

式(17)保证两个出口之间的间距应符合最小安全间距要求，公式为

(18)

式(18)限制可建的出口总数，公式为

(19)

式(19)确保某一类型飞机只能分配到同一个出口，公式为

yrk∈xk,k∈A(r)=1,2,…,R

(20)

式(20)保证飞机只能使用被选择的出口，公式为

(21)

(22)

用k(r)表示机型r所对应的最佳转出位置，机型r使用实际出口k的无效占用跑道时间Trk共分为两种情况：

(1)当Dk=k(r)时，机型r达到转出速度时可刚好从k出口驶出，Trk=0。

(2)当Dk>k(r)时，机型r达到转出速度后需再行驶一段距离，到达k出口驶出，Trk=[Dk-k(r)]/vex1；若飞机在端联络道驶出，Trk=2[Dk-k(r)]/(vex1+vex2)。

式中：ωr为r类航空器所占比例；N为候选出口总数；Trk为r类航空器使用k出口的无效占用跑道时间；A(r)为r类航空器的所有出口；Dk为出口k距跑道端距离；Dmin为两个出口之间的最小间距；vex1为从快速出口滑行道转出的最大速度；vex2为从端联络道转出的最大速度。

2.2 动态规划方法

动态规划方法是求解决策过程最优化的数学方法。其核心思想是将一个复杂系统问题分为若干个阶段，通过选取合适的决策变量，并构建指标函数和最优值函数，将多阶段过程转化为一系列单阶段问题一一进行求解[16]。快滑位置模型属于多阶段最优化问题，可采用动态规划思想进行求解。

采用动态规划思想对实际问题进行求解时，需要根据问题的实际情况抽象成动态规划相应术语，以便于分析计算。

(1)阶段。阶段是对问题研究过程的划分，一般按照时间或空间的特征划分阶段，并按照阶段的次序优化问题，常用k=1,2,…,n表示阶段变量。

(2)状态。状态表示在每个阶段过程所处的自然状况，需具备无后效性，即当前状态的变化与之前阶段的状态无关。描述状态的变量称为状态变量，常用xk表示第k阶段的状态变量。而根据过程的演变，状态变量可以是连续的或者离散的。

(3)决策与策略。当一个阶段的状态确定后，做出选择进入下一个阶段的决定称为决策，描述决策的变量称为决策变量，决策变量的取值范围称为决策集合。常用uk(xk)表示第k阶段处于状态xk的决策变量，Uk(xk)为决策集合。策略为决策组成的序列，由第1阶段至第n阶段的策略记作p1n(x1)，即

p1n(x1)={u1(x1),u2(x2),…,un(xn)}

(23)

(4)状态转移方程。如果给定某阶段的状态和决策，即可确定下一阶段的状态，其状态转移方程为

xk+1=Tk(xk,uk),k=1,2,…,n

(24)

(5)指标函数与最优值函数。指标函数用来衡量每一种状态的优良程度，以便实现更佳的决策。第j阶段的指标取决于状态xj与决策uj，用vj(xj,uj)表示。最优值函数为指标函数的最优值，根据实际情况可取最大值或取最小值。

递归方程和状态转移方程是求解动态规划问题的基本方程。递归方程表达式为

(25)

式(25)中：opt根据实际问题可以取最小值(min)或最大值(max)。

动态规划问题的求解过程一般是沿顺过程或逆过程的递推计算，下一步的最优决策都是在上一步的最优结果中进行，依次计算，直至最后一步，可输出全过程的最优值，即模型的整体最优解。

2.3 基于动态规划方法的模型算法设计

根据动态规划方法思想，对快滑位置模型做如下分析。

(1)划分阶段：假设某机场需要设置的出口总数为N，第k阶段表示已经设置了k个出口，还剩(N-k)个出口可以设置。

(2)确定状态变量：xk代表第k阶段中快速出口滑行道距跑道端距离，当k=N时，xk≡0。允许状态集合Xk∈(0,Ll)。

(3)选择决策变量：uk(xk)表示第k阶段处于状态xk时可供选择的xk+1，需满足|xk+1-xk|≥Dmin。

(4)设定状态转移方程：

xk+1=uk(xk)=uk(minTk)

(26)

(5)指标函数：

(27)

(6)顺序递归方程：

(28)

假设以一定的间隔设定出口位置，则对于每阶段状态变量xk，通过枚举所有可能的uk确定fk(xk)，相应的最佳决策变量uk一起存储，直至最后阶段N，得到最优决策变量uk*。求得快速出口滑行道最佳设置位置及加权无效占用跑道时间。基于上述分析，设计快速出口滑行道最佳位置算法，可利用MATLAB软件进行求解，其算法流程框图如图5所示。

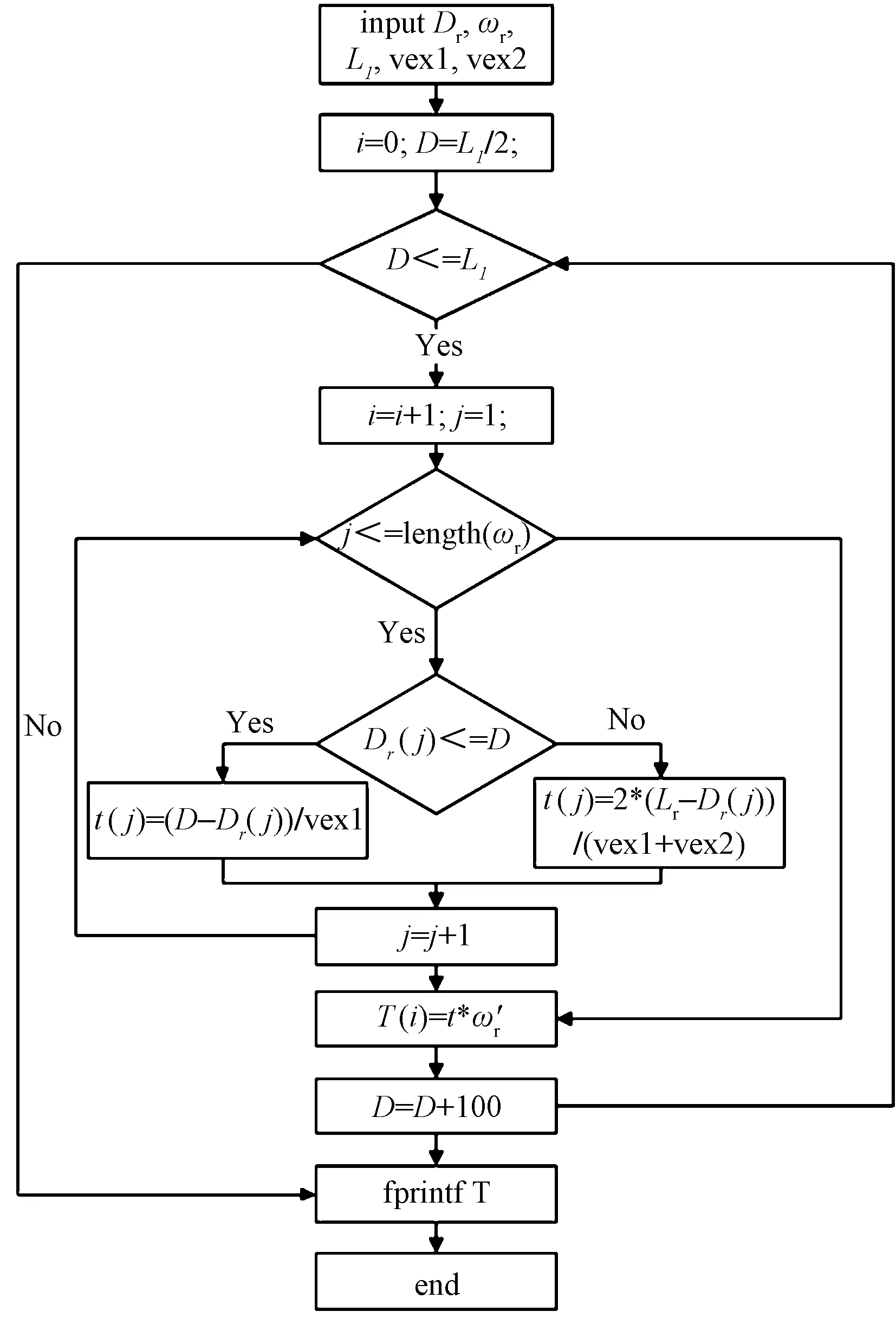
图5 滑行道最优位置求解流程框图Fig.5 Block diagram of the optimal solution for taxiway

3 实例分析

3.1 腾冲机场现状分析

腾冲机场飞行区等级为4C，跑道长度2 350 m，主起降方向为18号，跑道两端高程差为11.75 m，跑道纵坡为0.5%。18号跑道风速服从λ=1的指数分布，最高气温为25 ℃，最低气温为5 ℃，气压为89.13 kPa。该机场的起降机型、年起降架次根据历年资料皆可查询，但对于入驻的军用飞机并无任何历史资料，因此假设军用飞机入驻机型(A型、B型)及其年起降架次，以表征对应权重，如表3所示。

表3 18号跑道飞机运营数据

3.2 着陆转出距离计算

依据第2节所述理论，采用蒙特卡洛方法对军用、民用飞机最佳转出位置进行仿真计算，假设18号跑道需建设一个快速出口滑行道，角度设计为30°。采用MATLAB软件进行仿真，计算飞机着陆至达到转出速度所需要的跑道长度，将计算结果汇总如表4所示。

表4 军、民用飞机最佳转出位置

3.3 快滑出口最优位置计算

根据每种机型的比例和最佳转出距离，利用第3节所述算法，经过MATLAB软件求解计算，分别得到相同出口角度(30°)、不同出口位置情况下民用与军、民用机型加权无效占用跑道时间，如表5所示。

根据计算得到的不同快滑位置情况下民用飞机与军、民用飞机加权无效占用跑道时间，绘制不同出口位置与加权无效占用跑道时间的关系，以便分析快滑的最优设计位置，如图6所示。

表5 18号跑道最优位置分析

图6 快滑出口位置与加权无效占用跑道时间关系Fig.6 The relationship between the position of the fast exit and the weighted invalid occupied runway time

由图6可知，在18号跑道，若只由民用飞机使用，随着出口设置位置离着陆端变远，其加权无效占用跑道时间先减小后增大。当距离跑道端1 510 m时，加权无效占用跑道时间最小，为5.85 s，此时最优出口位置为1 510 m，民用机型皆可从此口转出，占其总起降架次的100%，军用机型皆不可从此口转出。当兼顾军用飞机使用时，最优出口位置变为1 650 m，加权无效占用跑道时间变为11.32 s，相比民用飞机使用时增加5.47 s。民用机型皆可从此口转出，占其总起降架次的100%，军用机型A可从此口转出，占其总起降架次的70%。可见，快滑转出位置经过调整后，无论是从加权无效占用跑道时间还是从使用该出口的民用飞机占其总起降架次的百分比来看，两者都变化不大，但使用该出口的军用飞机占其总起降架次的百分比可提高70%，能更好地满足军用飞机的使用需求。

因此，将18号跑道快滑出口位置应设置在1 650 m处，以保证在民用飞机正常使用的基础上，兼顾军用飞机的使用。由于跑道两端风速、起降架次等因素的不同，因此对于36号跑道，最佳快滑出口位置不一定在1 650 m处，但应用本文算法，同理可得到36号跑道最佳快滑出口位置，限于篇幅原因不再一一赘述。

4 结论

(1)分析了军用飞机与民用飞机的着陆过程，研究了飞机着陆过程中的影响因素，分为常量和随机变量两类，并对随机变量的分布规律进行了探讨。采用蒙特卡洛方法进行仿真，确定了各机型着陆转出的最佳位置。

(2)提出最小加权无效占用跑道时间概念，并以此为目标函数建立快滑转出位置模型，结合动态规划方法，设计了模型求解程序。模型求解程序既适用于新建机场，也适用于改扩建机场；既适用于一条快滑位置计算，也适用于多条快滑位置计算。

(3)通过算例机场分析，验证了模型的可靠性。结果发现相比只考虑民用机型使用时，无论是从加权无效占用跑道时间还是从使用该出口的民用飞机占其总起降架次的百分比来看，两者都变化不大，但使用该出口的军用飞机占其总起降架次的百分比可大幅提高。保证在民用飞机正常使用的基础上，能更好地满足军用飞机的使用。研究为军用飞机使用民用机场奠定基础，为民用机场预留军事功能提供技术支撑。