考虑土性相关性的软岩高填方路堤边坡稳定性分析

王 雷

中铁十九局集团第三工程有限公司 辽宁 沈阳 110136

软岩是在某种特殊环境下形成的具有较为明显的塑性变形的复杂岩石力学介质，通常可以根据该种介质的饱和单轴抗压强度判定，若饱和单轴抗压强度小于30 MPa，可以判定为软岩。软岩强度低，土质松散，孔隙度大，胶结程度低，负荷能力较差，易受外力作用影响。软岩在我国广泛分布，在软岩上铺设道路时，由于软岩的性质，其较差的稳定性会对道路施工、使用安全等造成影响[1]。软岩的力学性质对道路边坡的影响较路面影响更大。因此，在软岩地区的道路多采用高填方路堤来对道路边坡进行 防护。

高填方路堤是指在水稻田或长年积水地带，用填筑材料填筑的路堤高度大于6 m，在其他地带填方总高度超过18.0 m（土质）或超过20.0 m（石质）的路基。路堤边坡的稳定性分析在相关岩土工程中有重要的实际意义，采用传统的定值法分析边坡稳定性时，由于包含的不确定因素是随机的，若只依靠该种方法的分析结果，会出现边坡失稳的事故[2-4]。基于以上分析，本文将研究考虑土性相关性的软岩高填方路堤边坡稳定性分析方法。

1 考虑土性相关性的软岩高填方路堤边坡稳定性分析方法

1.1 建立软岩高填方路堤边坡模型

为实现对软岩高填方路堤边坡的稳定性分析，建立如图1所示的高填方路堤边坡模型。

在图1中，边坡高度、边坡坡脚、容重等参数都对边坡的稳定性有影响。不同类型软岩的参数不同，可通过查询相关文献资料确定。

结合图1和查询的参数，在ANSYS软件中模拟软岩高填方路堤边坡应力变化，如图2所示。

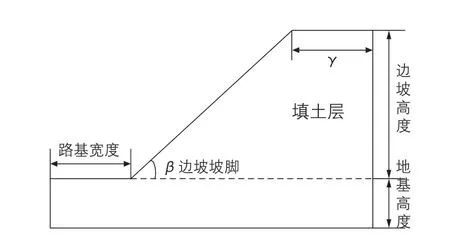
图1 软岩高填方路堤边坡模型

图2 边坡内应力示意

根据对边坡内应力模拟，可以分析出随着高填方的高度不断增加，边坡内部分应力不断增加，其水平位移不断增加，并且位移的垂直高度不断上移[5-6]。

由此确定，变化前后软岩高填方路堤边坡模型参数之间的关系如下：

式中：c——软岩黏聚力；

c'——变化后的黏聚力；

ωc——抗剪强度的描述因子；

φ——软岩的内摩擦角；

φ'——变化后的内摩擦角；

ωφ——变化强度因子。黏聚力c与内摩擦角φ是软岩的抗剪强度指标，具有一定的变异性，需要考虑两变量之间的相关性。

1.2 确定软岩土性相关性

土性参数黏聚力c与内摩擦角φ的相关性可以通过相关距离来确定[7-8]，根据Vanmarcke的理论，假设在局部空间中随机场的均值可以代替整体随机场的点均值，则软岩土性的相关距离可以按照下式计算：

式中：δn——软岩土性的空间自相关距离；

h——土性的方差折减系数，h≥1。

确定方差折减系数后，根据式（3）所示的自相关函数，预测空间场中与某一点的土性参数[9-10]。土性参数的自相关函数计算公式为：

式中：Δx——空间场中两点间的距离。

在实际应用中土层的土性不可能为均匀的，可以使用点方差，消除非均匀土性对土性的相关距离计算的影响。空间自相关距离δn越大，说明土性变量黏聚力c与内摩擦角φ呈负相关；空间自相关距离越小，说明黏聚力c与内摩擦角φ呈正相关。根据模拟分析，软岩中黏聚力c与内摩擦角φ呈正相关[11]。确定软岩土性相关性后，再对边坡稳定极限平衡进行分析。

1.3 软岩高填方路堤边坡稳定极限平衡分析

本文使用简化的Bishop法分析边坡稳定的极限平衡，图3为边坡受力分析示意。

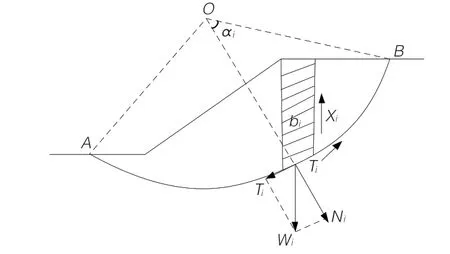
图3 边坡受力分析示意

分析可知，每一土条中受力不为静止，若忽略土条间的竖向作用力，则构建如下的受力平衡关系：

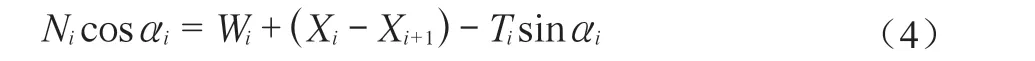
式中：Wi——第i条土条的自重；

Xi——Wi对边坡破裂圆面圆心的力臂；

Ti——剪切强度;

αi——第i条土条的破裂面与水平之间的夹角[12-13]。

假设软岩土条的抗剪强度与边坡滑动的切向力平衡，则可以得到最终软岩高填方路堤边坡稳定性系数FS计算式如下：

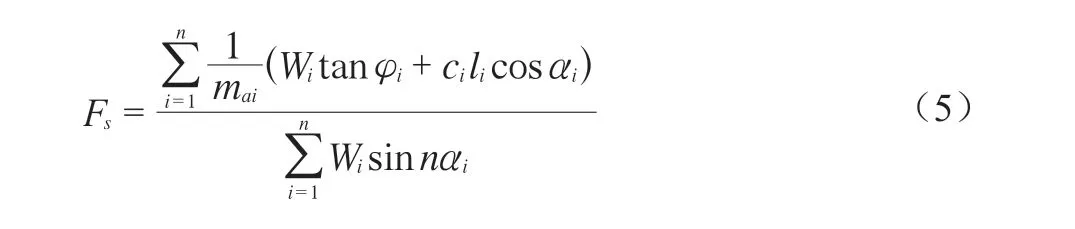
式中：mαi——与稳定性系数相关的参数，按照迭代法 求解；

ci、φi——第i条土条的黏聚力和内摩擦角；

li——土条破裂面的宽度[14-15]。

若对边坡稳定性分析数值邻近或大于上文计算的最大FS数值，则判断该边坡极度不稳定；若较小于FS数值，该边坡较稳定；若远小于FS数值，则边坡非常稳定。

以上为本文研究的考虑土性相关性的软岩高填方路堤边坡稳定性分析方法。

2 分析方法验证

本文研究了考虑土性相关性的软岩高填方路堤边坡稳定性分析方法。为判断该稳定性分析方法的优劣，设计相关试验步骤，完成试验验证。

2.1 验证内容

本次采用对比试验的形式，试验的对照组为传统的路堤边坡稳定分析方法，试验组为本文提出的考虑土性相关性的软岩高填方路堤边坡稳定性分析方法。对比试验的试验对象为一段长度为1 km的软岩高填方路段，将路段的两侧分为试验组和对照组。

对比试验的对比指标为2种分析方法的分析结果与Morgenstern-Price法分析结果之间的误差。按照试验验证过程，得到对稳定性分析方法的验证结论。

2.2 验证准备及过程

将1 km的试验路段均分为10组，并对其进行编号。试验路段具有一定的高度差，其具体参数如表1所示。

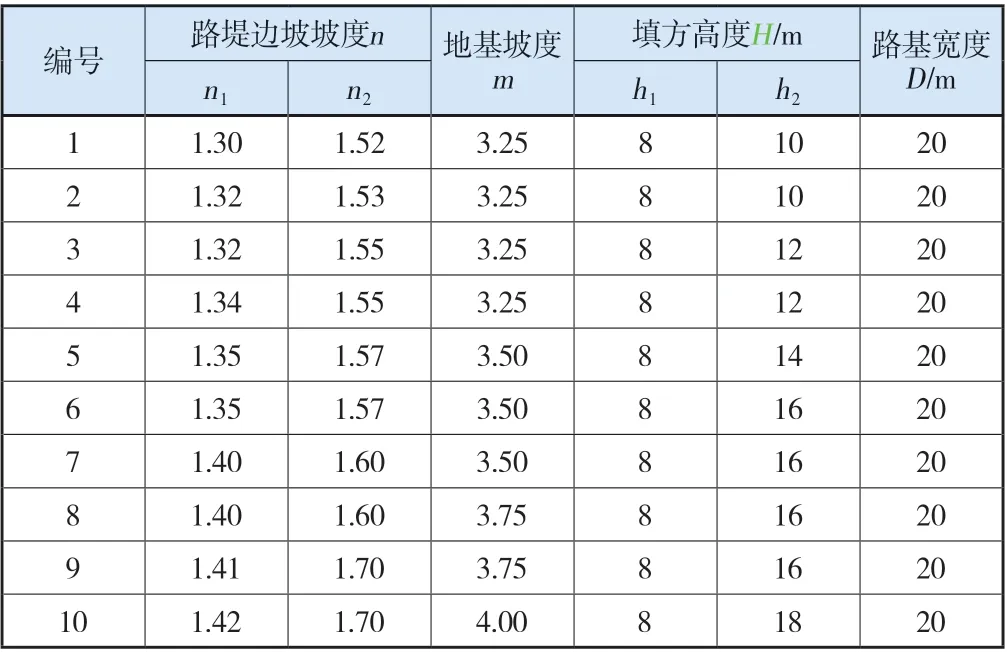
表1 试验路段边坡参数

本次试验中对试验路段边坡稳定性影响外界因素设定为水分含量，试验分别在天然状态和饱和状态2种软岩含水状态下完成。使用试验组和对照组2种稳定性分析方法分别对试验路段路堤边坡2种状态下的稳定性进行分析，并使用Morgenstern-Price法按照路段编号对试验路段路堤稳定性进行分析。

记录3种稳定性分析方法对试验路段路堤边坡稳定性分析后输出的稳定系数，对试验数据进行处理，分析试验组和对照组方法与Morgenstern-Price法之间的误差，判断对比试验中2种分析方法的优劣。

2.3 验证结果

对比在天然状态下和饱和状态下不同方法的计算数值结果。为验证本文所得结果的准确性，在试验前采用当前常用的Morgenstern-Price法，进行不同状态下边坡稳定准确系数的测算，并得到计算结果，以此为依据进行试验，分析并判断不同方法测得的数据结果。本次验证结果如表2、表3所示。

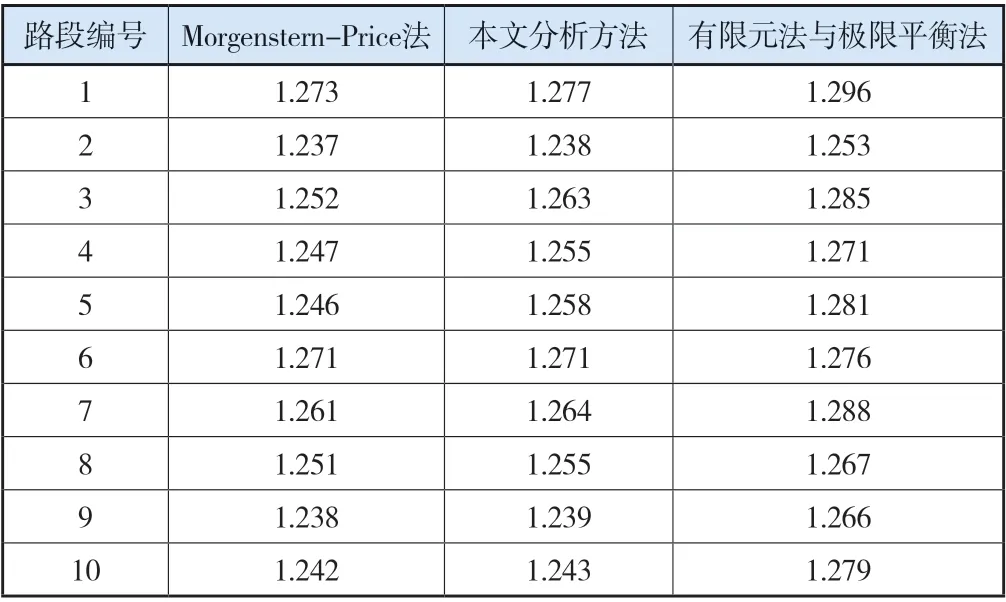
表2 分析方法对比结果（天然状态）

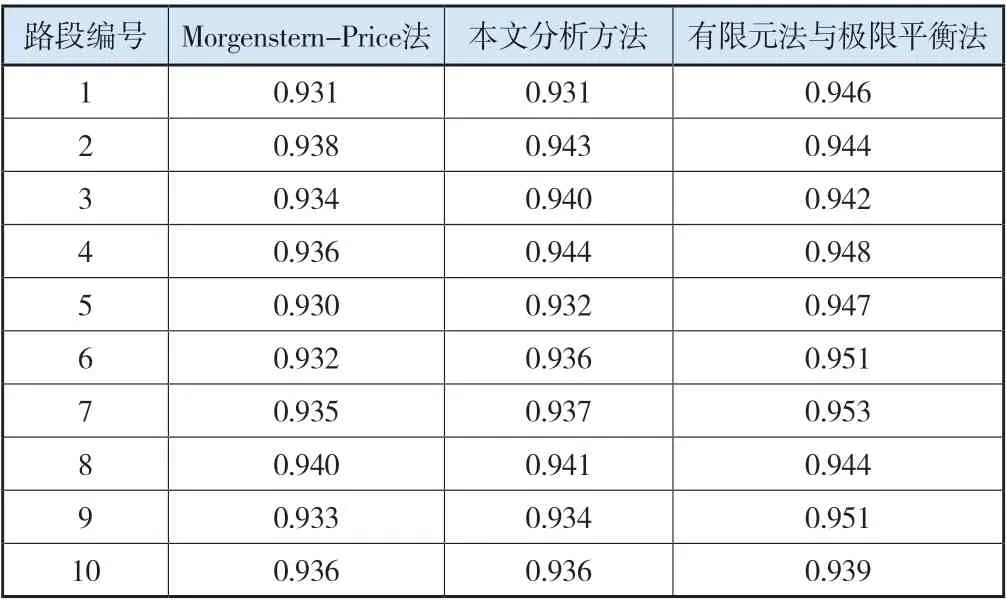
表3 分析方法对比结果（饱和状态）

分析表2可知，在试验路段处于天然状态下时，使用Morgenstern-Price方法得到的边坡稳定系数区间为[1.237,1.273]，使用本文分析方法得到的边坡稳定系数区间为[1.238,1.277]，使用有限元法与极限平衡方法得到的边坡稳定系数区间为[1.253,1.296]。从试验组和对照组2种分析方法的边坡稳定系数区间来看，本文方法的区间宽度更小，并且区间端点与Morgenstern-Price方法得到的边坡稳定系数区间端点更近。说明试验路段在天然状态下时，本文研究的边坡稳定性分析方法的准确度更高。

分析表3可知，在试验路段处于饱和状态时，使用Morgenstern-Price方法得到的边坡稳定系数区间为[0.930,0.940]，使用本文分析方法得到的边坡稳定系数区间为[0.931,0.944]，使用有限元法与极限平衡方法得到的边坡稳定系数区间为[0.942,0.951]。

本文分析方法的数值区间更靠近Morgenstern-Price方法的数值区间，并且每一组的数值误差都远小于有限元法与极限平衡方法的误差。说明在试验路段处于饱和状态下时，本文分析方法对边坡稳定性分析的误差更小，精度 更高。

综上所述，本文提出的考虑土性相关性的软岩高填方路堤边坡稳定性分析方法的分析误差更小，相比传统稳定性分析方法精度更高，具有优越性。

3 结语

软岩是我国比较常见的一种土质，对软岩高填方路堤边坡稳定性进行有效分析，对工程发展有重要意义。

本文研究了考虑土性相关性的软岩高填方路堤边坡稳定性分析方法，通过与传统稳定性分析方法的对比试验，证明了本文方法的稳定性分析误差更小，具有一定的优 越性。