边故障增广立方体通过指定边的无故障哈密尔顿圈

佘卫强

数学与应用数学研究

边故障增广立方体通过指定边的无故障哈密尔顿圈

佘卫强

（漳州职业技术学院 公共教学部，福建 漳州 363000）

增广立方体；线性森林；哈密尔顿圈；网络

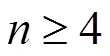
令

且

由0导出的子图是线性森林，则在AQ-中存在一条无故障哈密尔顿圈包含0的所有边。

1 引言

这里0连接0和0，1连接1和1。

2 定理1的证明

对作数学归纳法证明。

当=4时，由引理2得到，定理1成立。

设

下面分两种情况讨论，其它情况都同构于这两种情况中的某一种。

即存在

图1 (u,v)和(s,t)没有交点

图2 (u,v)和(s,t)有交点

包含0，如图3所示。

图3 ，

所以取

包含E0，如图4所示。

情况2 若

为方便表述假设

且

故在AQ-中存在一条无故障哈密尔顿圈

包含0，如图4所示。

定理1归纳法证毕。

3 结束语

[1] H C Hsu, L C Chiang, J J M Tan, L H Hsu. Fault Hamiltonicity of augmented cubes[J]. Parallel Comput- ing, 2005, 31(1): 131-145.

[2] S Y Hsieh, Y R Cian. Conditional edge-fault Hamilton- icity of augmented cubes[J]. Inform Sci 2010, 180(13): 2596-2617.

[3] 佘卫强,增广立方体中通过给定三条边的哈密尔顿圈[J].漳州职业技术学院学报,2015,17(3):10-15.

[4] Wang W Q, Chen X B. A faulty free Hamilton cycle passing through prescribed edges in Hypercubes with faulty edges[J]. Inform Process Lett, 2007,107(2): 211- 215.

[5] Chen X B. Cycles passing through prescribed edges in hypercubes with some faulty edges[J]. Inform Process Lett, 2007, 104(2): 211-215.

[6] Wang S, Y Yang, J Li. Hamilton cycles passing through linear forests in k-ary nn-cubes[J]. Discrete Applied Mathematics, 2011, 159(14): 1425-1435.

[7] 佘卫强,边故障增广立方体中两条无故障点不交路[J].闽南师范大学学报,2016,91(1):17-20.

[8] A Bondy, U S R. Murty, Graph Theorywith Applications [M]. Macmillan Press, London, 1976.

Fault-Free Hamilton Cycle Passing through Prescribed Edges in Augmented with Faulty Edges

SHE Wei-qiang

(Department of Public Teaching, Zhangzhou Institute of Technology, Zhangzhou 363000, China)

Augmented cube; Linear forest; Hamiltonian cycle; Network

O157.6

A

1009-9115(2019)06-0033-04

10.3969/j.issn.1009-9115.2019.06.008

国家自然科学基金项目（61603174）

2019-06-04

2019-09-22

佘卫强（1981-），男，福建东山人，硕士，副教授，研究方向为组合网络。

（责任编辑、校对：赵光峰）