基于层次分析法构建海洋工程方案比选模型
湛江南海西部石油勘察设计有限公司
传统的海洋工程方案多采用以经济评价为基础的专家意见评定方法确立优选方案。传统的经济评价通常仅考虑了经济效益,涉及因素较为单一,缺乏非经济因素的定量评价考量。海洋工程方案比选受多因素影响相互制约,单一考量经济因素不能全面反映方案的优劣。为解决这个多目标决策问题,本文致力于探索一种适应于海洋工程方案比选的数学模型,把相关的评价决策影响因素及其内在关系转化为定量数据信息,使评价思维更数字化、系统化、科学化。
1 层次分析法原理及适用条件
层次分析法是美国运筹学家SAATY 于20 世纪70 年代提出,它特别适用于分析解决一些结构比较复杂、难以量化的多目标决策问题。由于方法简单,能综合专家经验和意见,目前得到较多应用。层次分析法是一种在处理复杂的决策问题中将有关因素分解成目标、准则、方案等层次,用一定标度对人的主观判断进行客观量化的决策方法。该方法特别适用于分析解决一些结构比较复杂、难以量化的多目标决策问题[1]。
2 海洋工程方案比选模型
海洋工程方案比选是一项系统评价工程,涉及因素繁多,比选过程十分复杂,在建立评价比选模型时应尽可能客观准确地反映海洋工程开发各方面的实际情况[2]。其决策过程中涉及评价因素较多且不易定量,定性指标又互相影响的特点,与层次分析法适应性特征相符。因此,本文拟采用层次分析法来研究海洋工程方案比选的决策问题。
2.1 建立层次结构图
根据海洋工程的特点,构建层次分析模型。该模型顶层为目标层,中间为准则层(海洋工程系统复杂,每项准则还可细分为若干子准则),最底层为方案层。模型选取投资费用因素B1、技术因素B2、运营维护因素B3、安全及环境评估因素B4作为准则层一级指标,在此基础上细分为子准则层二级指标Ci[3]。然后根据目标层、准则层、子准则层、方案层,按该指标体系建立层次结构图(图1)。
2.2 影响因素两两比较
求本层次要素相对于上一层次要素的权重。将(子)准则层要素Ci和Cj(i,j=1,2,…,n)相对于上一层次要素A按重要程度进行两两比较,得判断矩阵(aij)n×m。影响要素两两比较时,确定了aij值的9 级标度,表1 中主对角线数字aii=1,且。

表1 aij 值的9 级标度Tab.1 9-level scale of aij value
2.3 建立判断矩阵
求判断矩阵的特征向量(w1,w2,…,wn)T,该向量标志要素C1,C2,…,Cn相应于上层要素A的重要程度排序。求特征向量可采用线性代数中的方法,在一般的应用中可以用近似算法进行,本模型选取求和法进行计算。先对判断矩阵的每列求和,令,并计算得到。

图1 层次结构Fig.1 Hierarchy structure
2.4 判断矩阵的一致性检验
计算最大特征值λmax,对判断矩形进行一致性检验,上述计算得到的wi能否作为下层要素对上层某一要素排序的依据需要检验判断矩阵中的aij值之间是否具有一致性,即∀i,j=1,2,…,n,有。其原理为wi标志第i个要素的重要程度,当判断矩阵具有一致性时,,判断矩阵可写为A=(aij)n×m,则有

n为特征值。当判断矩阵完全一致时有λmax=n,当判断矩阵在一致性上存在误差时有λmax>n,误差越大,λmax>n的值就越大。其中

层次分析法中用CI作为检验判断矩阵一致性的指标,其中
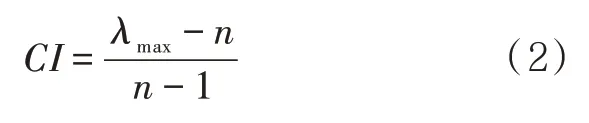
因判断矩阵的阶数n越大时,一致性越差,为消除阶数对一致性检验的影响,引进修正系数RI,并最终用一致性比例CR值作为判断矩阵是否具有一致性的检验标准[4]。其中

当计算得到CR值小于0.1 时,认为判断矩阵具有一致性。RI值随矩阵阶数n变化,见表2。

表2 1~15 阶平均随机一致性指标RITab.2 Average random consistency index RI order 1-15
如果判断矩阵均通过了一致性检验,列出Ci的所有准则相对于目标的判断矩阵并计算出权重向量,最后通过综合计算得出结果对方案进行排序优选。
3 案例分析
3.1 案例背景
H 油田位于渤海东约25 km 的海域,平均水深约35 m。该油田是我国渤海北部海域早期投入的油田,产量递减较快。为了解决油田增产迫切要求和提高老油田的经济效益,油田地质研究加强挖掘潜力,需采取措施以增加储/产量,使油田保持稳产。通过测量计算,该油田新增4 口井即可满足增产作业需求。目前,H 油田有一个H 综合平台为该油田进行采集、计量和综合处理。由于H 平台原有井位已满,未预留井槽,故须新增4 个井槽[5]。针对该项目,制定出了3 个备选方案进行比选。
3.2 方案概况
3.2.1 新建井口平台(方案一)
采用传统方案,新建1 座4 腿导管架简易井口辅助平台H-WHP,与原有H 综合平台通过栈桥连接,新增井槽16 口,其中12 口为未来增产之用。H-WHP 平台海上设计、建造和安装周期需要24~28 个月,预计建设投资为4 500 万元,年运营维护费为150 万元。新建4 腿井口平台如图2 所示。

图2 4 腿井口平台Fig.2 4-leg wellhead platform
3.2.2 新增外挂井槽(方案二)
在H 综合平台井口区南侧增加4 口调整井,由于没有预留井槽,需要增加4 口井的外挂井槽。该方案改造周期为10~12 个月,预计改造成本为880万元,年新增运营维护费为50 万元。其缺点包括:外挂井槽位于导管架外侧,容易受到外来船只的碰撞,须采取防碰撞措施保护井口;井口片多采用管夹螺栓连接形式,油田作业者须定期检测井口片。新增外挂井槽如图3 所示。
3.2.3 新增内挂井槽(方案三)
在H 综合平台井口区东侧增加4 口调整井,由于没有预留井槽,需要增加4 口井的内挂井槽。该方案改造周期为13~15 个月,预计改造成本为750万元,年新增运营维护费75 万元。缺点是井口片多采用管夹螺栓连接形式,油田作业者须定期检测井口片。新增內挂井槽如图4 所示。

图3 新增外挂井槽Fig.3 Newly added external hanging well groove

图4 新增内挂井槽Fig.4 Newly added inner hanging well groove
3.3 方案措施
为解决三个方案存在的难点,采取以下相应的解决措施。
方案一:新建井口平台。
方案二:新增外挂井槽。在水平面以下的水平层,若按每口井槽设计独立管卡的方案,没有足够的空间固定和安装管卡;需要对H 综合平台进行整体校核和局部校核;外挂井槽水平下结构与H综保平台导管架无法采用焊接固定连接。由于原井口导向结构的影响,相应轴的水平杆件没有足够的空间固定和安装管卡,因此,考虑采用整体井口片方案;增加设计人员的校核工作量;采用水下大结构管卡使外挂井槽水下结构与导管架进行连接,连接过程只需用螺栓固定,施工便捷。
方案三:新增内挂井槽。新增4 口内挂井槽与H 综合平台井口中心距只有1.5 m,原有平台的井口间距为2 m,新增井口区空间狭窄,φ20 in(1 in=25.4 mm)的隔水套管无法安装;由于空间问题导致使用φ13.5 in 隔水套管,该尺寸的隔水套管无法满足水线附近的抗冰强度要求,且隔水套管是固定在原H 综合平台导管架的水平层上,其固定点的间距无法随意调整;尽管采用小尺寸隔水套管,还是无法避免隔水套管与导管架水平层的杆件相碰;隔水套管在泥线处与导管架结构和防沉板有干涉,且由于考虑导管架的强度校核和施工便捷,对该层导管架结构作改造的方法不够理想。经与钻完井部门讨论后决定将隔水套管的尺寸改为φ13.5 in;将邻近水线的上下两层的导向筒合二为一,设计成整体导向筒,飞溅区整体导向筒的设计顺利解决了小尺寸隔水套管的抗冰强度问题;在确保导管架整体强度不会减弱的前提下,对导管架局部杆件进行截除,杆件局部截除后该处的4 个套管可采用整体井口片固定,该井口片对原导管架整体强度反而起了加强作用;经与钻完井部门沟通,在满足钻井要求的前提下,仅对受套管安装影响的防沉板作局部切割,并将隔水套管切割成略带斜度。经过技术难点分析制定出具体方案:该外挂井槽与原有H 综合平台的4 个水平面层进行固定连接,水平面以上的3 层井口片采用焊接方法与H 综合平台固定连接,水平面以下的1 层井口片采用螺栓进行固定,并经过2 个大关卡将整体井口片与原H 综合平台水平杆件固定连接。该方案的海上安装不需要动用浮吊,只需利用油田守护船作为海上安装及潜水支持船,采用自制简易扒杆、滑轮即可完成水上及水下两部分外/内挂井槽的安装,大大降低了海上安装作业费用。

表3 三个方案因素分析对比Tab.3 Analysis and comparison of factors in three schemes
三个方案因素分析对比见表3。
3.4 建立层次分析评价模型
3.4.1 构建层次分析结构
根据海洋工程的特点,运用层次分析法进行分析,从而建立海洋工程层次分析结构(表4)。

表4 海洋工程层次分析结构Tab.4 Hierarchical structure analysis of marine engineering
3.4.2 建立因素判断矩阵
(1)A-Ci准则层指标权重计算。由专家们对三个方案的子准则层C1~C15进行打分评价,取其平均值,得到判断矩阵A。并由计算得到


(2)因素判断矩阵特征向量W的计算。上式各行之和为31.504 9,使之标准化后矩阵判断A的特征向量W为

从上式可推导出,WB1=0.368 5,WB2=0.310 3,WB3=0.023 7,WB4=0.297 4。显而易见,在拟定方案的准则层因素指标中,投资费用最重要,其次为技术因素,再次为安全及环境评估因素,运营维护的影响最小。
3.4.3 建立方案判断矩阵
(1)根据方案特征及难点,专家们对子准则层15 个指标的方案进行分析对比,分析情况如表5所示。
(2)专家们分析方案后根据表1 中的层次分析评价指标进行打分并取平均值,并按子准则层的因素Ci分别对方案层进行两两比对,建立方案判断矩阵A1~A15。

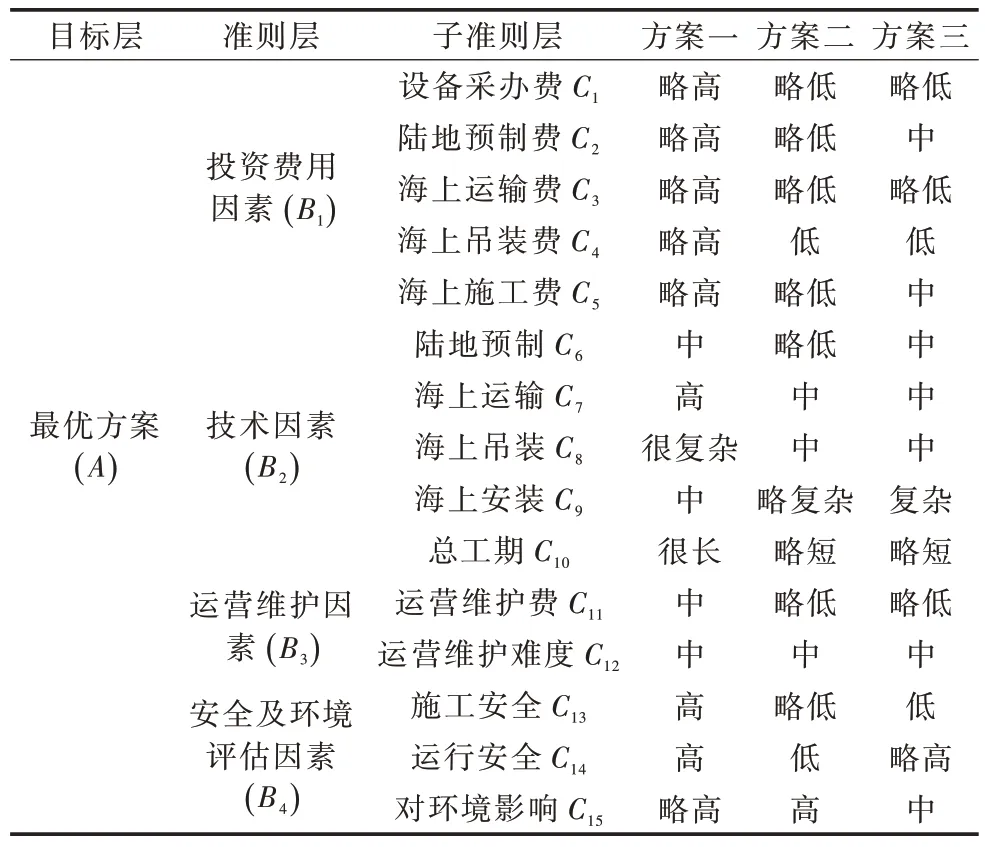
表5 各因素指标方案两两对比Tab.5 Pairwise comparison of various factors of schemes
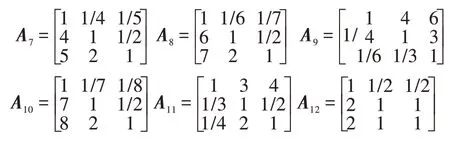

(3)参考判断矩阵A的特征向量计算方法,可求出判断矩阵A1~A15的权重向量为

3.4.4 建立综合判断矩阵
(1)构造综合矩阵C。

(2)计算向量

从上式得Wf3=0.393 4 >Wf2=0.348 4 >Wf1=0.258 3。结果表明,综合(子)准则层的因素指标后,方案三最优,方案二次之,最不值得推荐的是方案一。
3.4.5 判断矩阵的一致性检验
(1)计算向量Aw。
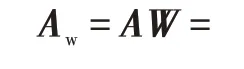

(2)计算λmax和CI的值。因素判断矩阵A的阶数为15,得到

(3)查随机性指标RI数值表(表2),找到对应的RI值后计算CR的比值。CR=CI/RI=0.065 3<0.1,故判断矩阵的一致性符合要求。如果CR>0.1,则需要重新进行判断,确定新的判断矩阵。
通过层次分析模型计算,推荐新增内挂井槽为最优方案。
4 结束语
海洋工程具有投资规模大、难点多、建设工期长的特点,涉及技术、造价、运维等多方面因素,具有很强的综合性和系统性。本文基于层次分析法建立了海洋工程方案比选模型,探讨解决方案比选的决策问题,并针对案例进行模拟分析,较好地验证了该评价模型可靠合理,切实可行,为海洋工程方案比选决策提供了一条新思路[6]。

