旋转式能量回收装置内部泄漏规律的解析计算

王 越，何之颂，周 杰，李文杰，徐世昌

(1.天津大学化工学院，天津 300350；2.化学工程联合国家重点实验室(天津大学)，天津 300350；3.天津市膜科学与海水淡化技术重点实验室，天津 300350)

随着反渗透海水淡化(SWRO)技术的不断发展，水资源短缺问题已经得到了极大的减缓[1-3].此外，得益于能量回收装置(ERD)的引入，海水淡化系统的运行能耗成本大幅降低，水的生产成本也降低到每立方米约 0.5～2.0美元[4-6].其中通过帕斯卡原理构建的旋转式能量回收装置(RERD)是当前最主流的装置类型之一[7-9].虽然 RERD具有结构简单、占地少的优点，但在 RERD的转子与端盘等部件微配合间隙中存在的典型内部泄漏问题，降低了能量回收效率这一关键性能[10-11].尽管在解决转子内漏的问题上已经投入了很多研究，但是现阶段的改善手段均处在穷举性实验的经验积累阶段，并未形成体系化的理论，因而工作效率较低且普适性较差.于是，将RERD装置中泄漏过程理论化成为了当前的重点方向之一.

在 Liu等[12]估算全回转式能量回收装置泄漏流量的流体力学表达式中，由于所表达的泄漏路径较RERD更为单一，所以不能完整表达 RERD中的泄漏过程.为建立和完善RERD的解析模型，考虑借鉴其他系统化的、与 RERD泄漏同为恒厚液膜流动过程的理论体系.在机械密封领域，宋鹏云等[13]通过解析 N-S方程阐述了其中恒配合间隙端面间的流体特征；Velescu等[14]通过流体动力学方程，描述了不可压缩流体在自润滑轴承中恒高度层流运动的压力、速度分布场，也实现了恒厚液膜解析模型的构建.然而，由于机械密封和自润滑轴承体系中的速度假设条件与 RERD环境中的不相符，上述过程的结果因而不能直接应用于RERD装置.

本文将 RERD泄漏过程的特异条件与上述体系中的解析原理相结合，并导出相应的流量、压力场表达式，同时完善 RERD系统的泄漏解析模型，从而为RERD中泄漏规律解析以及减缓泄漏的研究提供体系化的理论基础.

1 RERD介绍

图1中展示了本文的研究对象RERD中的核心部件的装配体，其中转子和海水侧端盘经过半剖表达.在 RERD中，转子、套筒和一对端盘构成了RERD的功能部件.在盐水侧的端盘上有两个分别对应着高压浓盐水以及泄压盐水的端口，同样在海水侧的端盘上也在相同位置具有与原料海水和增压海水联通的端口.转子被安置在海水侧端盘、盐水侧端盘及套筒配合组成的圆柱体空腔中，并与其中空腔的任意表面均保持着设定的配合间隙.转子内部共有 12个绕轴对称的轴向通孔，端盘的每个端口可同时覆盖5个连续孔道，剩余的2个孔道则被高低压流通区之间的密封缓冲带覆盖[15].

图1 RERD中核心功能部件的半剖装配图Fig.1 Assembly diagram of the core functional structure of RERD in half section view

在 RERD运行的过程中，并未完全将其中的高低压流域完全独立隔开，而是采用间隙密封的形式隔离这两部分流体.因此在装配体中必会发生从高压流域向低压流域的泄漏，这严重降低了装置的能量回收效率.由于泄漏的发生，流体将充满装置的配合间隙，所形成的液膜为连续泄漏提供了路径.由于压差是泄漏过程中主要的推动力，因此 RERD装置中高压流域必定是泄漏的源头，同时高压流域的边界为各泄漏流体的泄漏起点.

2 模型建立

2.1 物理模型的建立

为深入解构 RERD中泄漏流体的主要特征，笔者根据典型的RERD结构建立了RERD泄漏过程物理模型.图2(a)和(b)分别展示了海水侧RERD装配体的正视半剖图和海水侧端盘的俯视图.在该物理模型的基础上，笔者以转子的海水侧端面的圆心为柱坐标中r方向和θ方向的原点O，建立了三维柱坐标系下的 RERD泄漏物理模型，并且给出了在此坐标系下物理模型中的各项物理参数.其中柱坐标z向的正方向为图 2(a)中所示竖直向上方向，极轴的方向如图 2(b)中所示，并且r向以远离极轴原点为正，θ向以逆时针为正.

在图 2的物理模型中，高压流体p2分布于径向范围为r2～r3，在周向上的极角范围为θ2～θ3的高压集液槽中.而低压流体p1分布在径向范围为r2～r3，在周向上极角范围为[θ5，2π+θ0]的低压集液槽以及半径为r1的轴孔内.转子与端盘之间保持着轴向高度为h的配合间隙，同时在转子的外围，即半径为r4之外的区域，转子与套筒之间也保持着厚度为h的配合间隙.

图2 泄漏过程物理模型Fig.2 Physical leaking model

2.2 计算模型的建立

由于本文中的泄漏过程为通过狭缝间的恒厚液膜流动，于是可通过求解Reynold方程的解以得到该工况下压力和速度的分布[16].

式中：p为压力；h为高度；μ为动力黏度；θ′为时间；ω为角速度.

为了求解该偏微分方程的数值解，本文通过将上述物理模型进行网格划分处理，以得到数值求解过程需要的求解结点.笔者选择网格划分软件“Pointwise”实现物理模型的拓扑分析，并同时生成网格，然后用流体计算软件“Star CCM+”以求解计算.通过取迭代至残差为10-5以下时的 CFD计算值为最终数值求解结果.

2.3 泄漏模型的建立

根据第2.1节中所建立的RERD物理模型，笔者通过CFD计算了典型RERD结构在高低压边界分别为6.0MPa和0.2MPa，密封配合间隙为0.02mm，转子转速为600r/min，处理量为35t/h等操作条件下的计算结果.其中RERD的结构参数如表1所示.

图 3分别给出了给定操作条件下海水侧端盘端面上液膜内流体的的流线和压力分布云图.从图3(a)中可以清晰地观察到，从高压集液槽出发的泄漏流体在流动形式上受端面旋转的影响并不显著.并且端面上的流动形式主要为两种压力和速度场均十分典型的类型：从高压集液槽的内径侧泄漏往中心轴孔的区域，以及从高压集液槽外径侧泄漏往环隙液膜的区域内的端面径向流动；从高压集液槽的周向范围的边界线流往相邻低压集液槽边缘的区域内的端面周向流动.此外，从流线图可以看出高压流体并不直接泄漏往低压集液槽的外径边界上，因此只有环隙中的流体会且仅会泄漏往低压集液槽的外径边界上.

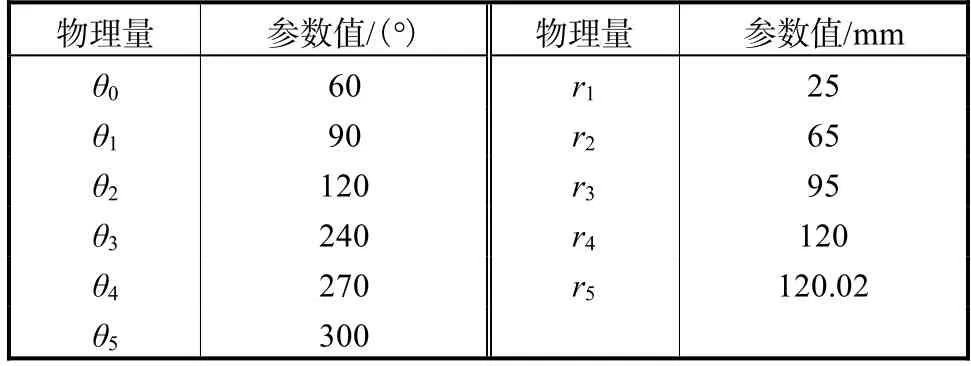
表1 RERD结构参数Tab.1 Structure parameters of RERD

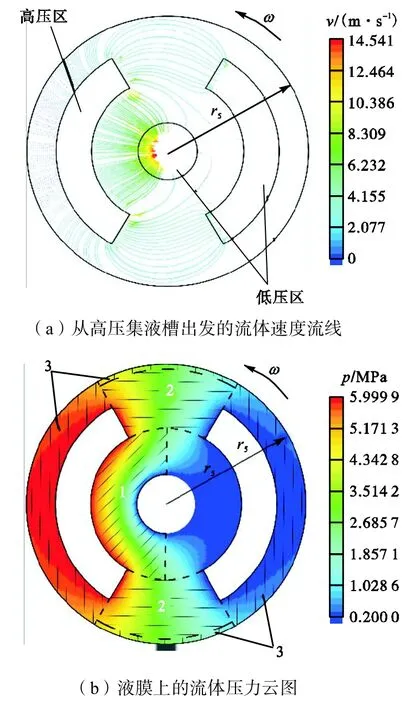
图3 端盘上的液膜(对环隙液膜的表示经过放大)Fig.3 Liquid film on the end cover(with amplified expression of annular film)

由图 3(b)中可知，只有高、低压集液槽外径外侧的压力场上存在指向环隙液膜方向的径向压降.这意味着，环隙中流体泄漏往低压集液槽的方式和高压流体从集液槽外径泄漏往环隙的形式相同，均为径向流动的形式.

环隙液膜由于轴向两端边界几乎完全对称，因此并不具有宏观上的轴向动力.此外，由于环隙在不同位置上分别与不同压力的流体相联，因而具有了在这两个联通位置之间的周向压差.在周向压差的推动下，液膜中的流体表现为周面周向流动的形式，这是RERD装置内存在的第3种泄漏形式.

除具有上述3种典型流动特征的主体区域之外，在 RERD的液膜中存在着受这些区域交叉影响的非主体复合区域.这些复合区域尽管覆盖面积不大，但鉴于难以精确描述也因此给 RERD泄漏模型的建立带来了阻碍.于是为了在泄漏模型中描述这些区域，笔者将以具有典型特征的流动形式近似表征这些复合区域.此外，由于在轴孔右侧和低压集液槽内径之间不存在流体流线，并且在压力云图上不具有明显的压差，因此该区域可视为几乎不存在泄漏流体.

综上，在RERD中的配合间隙中主要存在以下3条泄漏路径.

路径 1，即端面径向泄漏.高压流体从高压集液槽内径圆弧线沿径向泄漏往轴孔左侧.路径 1在周向上的范围为θ2～θ3，在径向上的范围为r2～r1，为图3(b)中斜线阴影所示区域.

路径 2，即端面周向泄漏.高压流体从高压集液槽的边线沿着周向泄漏往低压集液槽的边线.路径 2在周向上的范围为θ0～θ2和θ3～θ5，在径向上的范围为r2～r4，为图3(b)中横线阴影所示区域.

路径 3，即周面周向泄漏.高压流体从高压集液槽的外径沿着径向泄漏往环隙，并在环隙中沿周向泄漏往低压集液槽的外侧的环隙，最后沿着径向从环隙泄漏往低压集液槽的外径上.路径 3的径向流动部分的周向范围为θ5～θ0和θ2～θ3，径向范围为r3～r4；周向流动的部分的周向范围为θ0～θ2和θ3～θ5，径向范围为r4～r5，为图3(b)中竖线阴影所示区域.

3 解析计算

由第2.3节的结论可知，RERD中泄漏路径1、2和3主要表现为3种流动形式，即端面径向流动、端面周向流动和周面周向流动.对这 3条路径的解析计算需要首先解析这3种流动形式.

为方便各路径的解析计算过程，笔者根据实际工况中的流体特点对本文所讨论的物理模型提出了以下的假设条件[17].

假设1 RERD中配合间隙很窄，狭缝中流体的雷诺数Re很小，且其流动形式近似为二维层流运动，故流体在轴向上满足uz=0.

假设2 流体物理性质稳定，即ρ≡C1，μ≡C2.

假设4 在独立的径向泄漏中，流体的特性几乎完全关于z轴旋转对称，即流体各项参数均不随θ而变化，即.

假设5 装置中的流体由于只受重力场的质量力，则在轴向上有z=-g；在r和θ方向上不具惯性力，即R=0，T=0.

3.1 端面径向泄漏

端面径向流动的流体主要表现为保持一定轴向高度的沿径向辐射状收敛的流动形式，类似于机械密封或者润滑轴承中的流体特性.通过流体运动方程，即 N-S方程和连续性方程，即式(2)、(3)，即可得到该形式的流体特征方程，其形式为

式中：fB为质量力；ν为运动黏度；u为速度；ρ为密度.

本节所讨论泄漏流体的主要流动方向显然位于柱坐标中的r方向.因此，选取该方向上流动方程和连续性方程的分解形式作为本文讨论的重点，并且运动方程在本文的实际工况中可写为

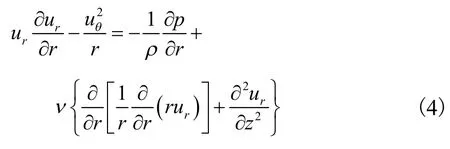
其中连续性方程式可写为

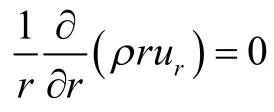
或

由于 RERD配合端面中的周向速度由动环旋转所产生的流体黏性力所提供，所以对于流体的周向速度显然有，且0≤z≤h.

N-S方程在柱坐标中的z方向上的分解形式可写作

基于式(6)可得出方程(4)中的∂p/∂r项具有如下特点.

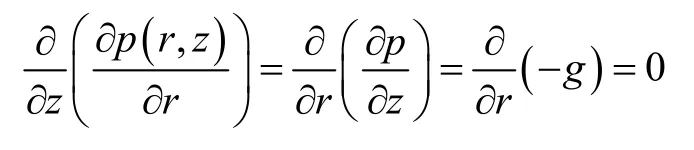
根据以上结论，可将流体的运动方程(4)整理为ur对z的2阶偏微分非齐次非线性方程的形式，即

该方程即为在能量回收装置中径向泄漏的基本方程.RERD的各项操作参数通常具有特定的取值范围，例如压力通常不低于 6.0MPa，转速通常只有几百转；端面间的配合间隙通常为 10-2mm级别.相比机械密封或润滑轴承这些具有完善解析理论工况的操作参数，本文工况中操作参数的取值范围与之截然不同.因而在 RERD操作条件下方程(7)中各因子间具有特定的量级次序，可总结如下.

(1)端面间的流体在速度分量上表现为ur≈uθ，故.

(2)方程(7)的常数项部分在量级分析中具有如下关系：

式中方程右侧为常数项.

将式(8)经过二次积分，可得出ur与z的关系.

由于在径向上，本节所考察的圆周径向泄漏过程满足质量守恒，即任意的圆柱横截面通过的流量并不随半径位置的变化而变化，该流量计算式为

由于Vq为与r无关的常数，故可将式(9)对r积分.

或

且

因此路径 1和 3中的恒配合间隙端面径向泄漏过程的流量如式(10)所示，压力场的分布如式(11)所示，其中r1≤r≤r2.

3.2 端面周向泄漏

端面周向的流体由于仍表现为沿着周向方向的带状流动形式，故与径向的泄漏过程同理，可引用NS方程对该过程进行研究.

同理于第 3.1节中的假设 2，此时端面上的流体在径向上受的离心力远远小于在周向上的作用力，即本小节仍满足如下假设.

假设 1 径向上发生的流动驱动力和流体速度相对于周向可忽略不计.

在此基础上，可写出在柱坐标中的θ方向上的流体运动方程以及连续性方程的分解形式分别为

对于其中的p项，由于流体轴向尺寸过短，则轴向质量力对流体的影响几乎可以忽略不计，也因此p并不是与z相关的量，所以，为了简化方程中uθ与r的关系，提出了假设2.

假设 2 在本文的操作条件中，p随径向的变化程度，远远不及p本身的量级.

由假设 2，p在径向上的变化可忽略不计.由于压力在径向上不发生变化，因此影响uθ分布情况的推动力，只能来自于转子旋转端面所产生的流体黏性力.即在r方向上.则方程(13)中除了变量之外均为常数，故方程(13)可化简成

式中：uθ满足，且ai为常数；方程右边为与变量z无关的量.将uθ代入式(14)并经过二次积分，可得出uθ与z的关系，即

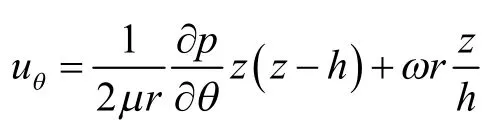
由周向上的质量守恒，故可得表达式

显然，方程中各项参数均与θ无关，将方程对θ积分后即可得到周向泄漏过程中压力与流量的表达式为

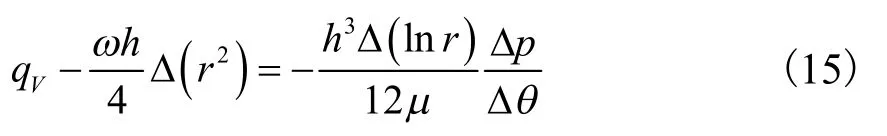
且

式中：r2≤r≤r3；θ0≤θ≤θ1.

此外，为验证本小节的假设 2，可写出 N-S方程在该环境中柱坐标r方向的分解形式，即

而利用式(15)和式(16)可写出此时的速度分布表达式为

将式(17)和式(18)联立，并将所得结果对r积分，即可得压力在径向上的变化量为

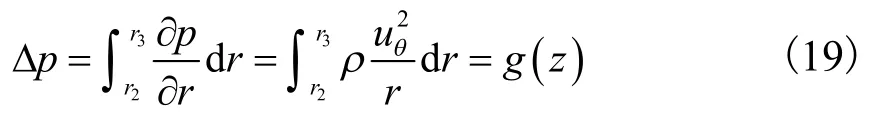
3.3 周面周向泄漏

在 RERD的周面液膜上进行着的主要是在环隙液膜中发生的周向流动过程，该过程亦可通过求解流体运动方程得到对应的流体特性.

显然，由于该过程中的流体速度方向吻合于柱坐标中的θ方向，于是可将θ方向上的运动方程以及连续性方程分别表示为

由于本节 N-S方程在r方向上的表达式与在第3.2节中的相同且均为方程(17)，故可知在本节中压力随径向的改变量仍只与离心力大小有关.同时离心力所起的作用对压力本身而言很小，且液膜的径向尺寸也很小，故离心力对压力的变化仍可忽略不计.因此p与均不与r相关.故可解二次常微分非齐次线性方程(20)，得到uθ与r的关系为

式中r5=r4+h.

由于流体在周向上满足连续性，故可计算出该过程的流量为

显然，等式中的各项因数均不随θ变化，则将该等式对θ积分，可得到环隙泄漏过程中压力和流量的表达式分别为

式中θ0≤θ≤θ1.

4 准确度验证

针对本文提出的 3种不同类型的泄漏路径解析表达式，为表征解析模型的可靠度，需要首先表征解析表达式描述3条路径各主体区域，即具有典型流动形式的区域的准确度.

为验证式(10)、(11)对径向泄漏流动形式表达的准确性，笔者根据典型的 RERD参数以及上述公式中的变量设计了如表2所示的操作条件，并在此基础上比较了在同一操作条件下公式与CFD的计算结果.

图4给出了通过CFD计算的工况1下液膜的压力分布云图.由图可见，在液膜上压力沿周向几乎完全不变，这意味着在第3节中的假设4对于径向流动的流体特性关于z轴旋转对称的假设成立.此外，由压力云图可知，在径向外侧的等压线显然与内侧不同，这意味着压力与径向位置呈非线性关系.这与解析模型中压力与径向位置呈非线性关系的现象相符.

表2 用于验证分析径向泄漏过程的操作条件Tab.2 Operation conditions of verification and analysis for the radially leaking process

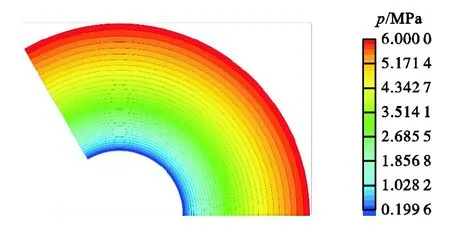
图4 工况1下液膜的CFD压力云图Fig.4 CFD pressure cloud on the film of case 1

图5给出了6组不同工况条件下，通过解析表达式和CFD两种方式所计算得到的不同工况下的液体压力分布规律，结果表明两种方式分别计算得到的压力曲线之间的相关系数不低于 99.99%，证明解析式能准确表达液膜的压力.

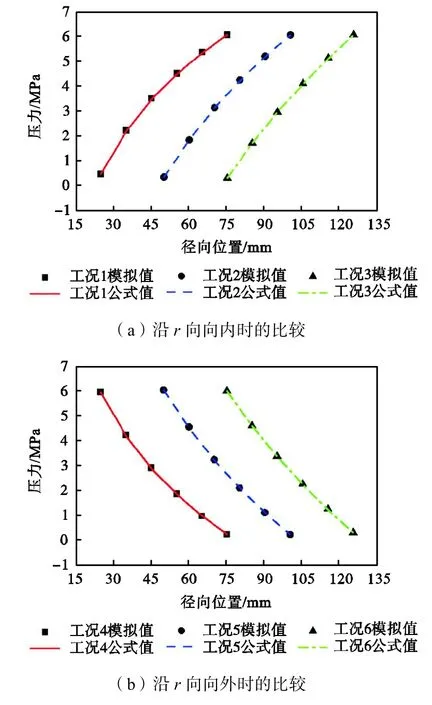
图5 径向泄漏时压力在径向上的分布Fig.5 Pressure variations in the radially leaking process

由图 6给出的不同计算方法得到的流量结果可以看出，通过两种方式所计算的流量之间非常相近，两者的相对偏差为6.41%～11.09%.并且通过比较可以看出即使是发生不同数量级流量的泄漏过程，该模型依然同样具有可靠性.说明本文构建的解析模型能准确预测径向泄漏的流量.尽管配合间隙值对流量值影响显著，但泄漏方向为沿r向的负方向、间隙值为0.02mm的工况1～3条件下的平均相对偏差为7.34%，与泄漏方向沿r向正方向、间隙值为0.01mm的工况 4～6条件下的平均相对偏差 8.93%相当接近，显示模型准确度并未因泄漏方向和间隙值的改变而受到显著影响.此外，在图 6中，解析模型的计算值通常略低于CFD的结果值.这是因为在CFD仿真时，高低压主流通区与液膜相联通的边界上发生的边界扩散为泄漏提供了额外的动力，解析模型中并未考虑这一扩散因而计算结果略低于CFD值.

图6 径向泄漏中的泄漏量计算值Fig.6 Calculated leakage in the radially leaking process

此外，为了验证解析模型对 RERD中周向泄漏过程的表达准确度，本文设置了如表3所示的验证条件范围，同时取液膜厚度为 0.02mm.通过比较用解析模型的式(15)、(16)和(20)以及 CFD 模拟两种方式所计算出的各工况条件下流量和压力关于极角的分布规律，进而验证解析模型对周向泄漏过程规律表达的准确性.

图7给出了工况7条件下通过CFD计算的周向泄漏过程的液膜压力分布云图.很显然，压力云图中等压线并不随着极角的变化表现出明显的疏密变化，这种压力随极角接近线性的分布与解析式中的线性分布结果相符.此外，压力云图中的等压线几乎均为指向圆心的径向线，这意味着压力在径向上并不发生明显的变化，故本文的解析模型在第3.2节提出的假设2成立.

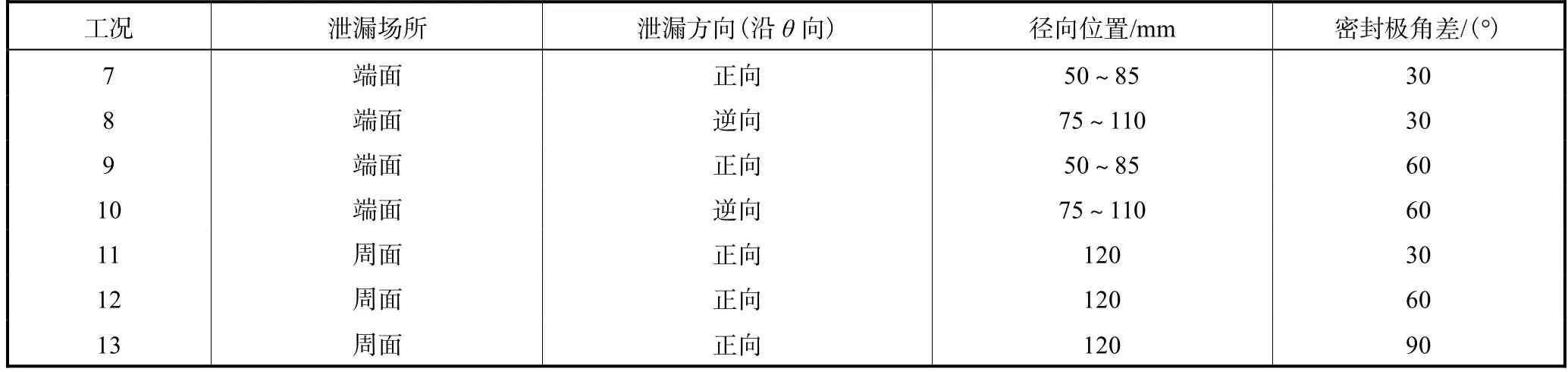
表3 用于验证分析周向泄漏的操作条件Tab.3 Operation conditions of verification and analysis for the circumferentially leaking process

图7 工况7下液膜的CFD压力云图Fig.7 CFD pressure cloud on the film of case 7

在图8中，压力随极角的分布曲线显然为线性分布，同时证明了第 3.2节中假设 2的成立.并且，通过比较两种方式所计算得到的压力分布曲线可知，两者间的相关系数高达 99.99%，这证明了解析模型能准确表达在端面周向泄漏过程中的压力分布.

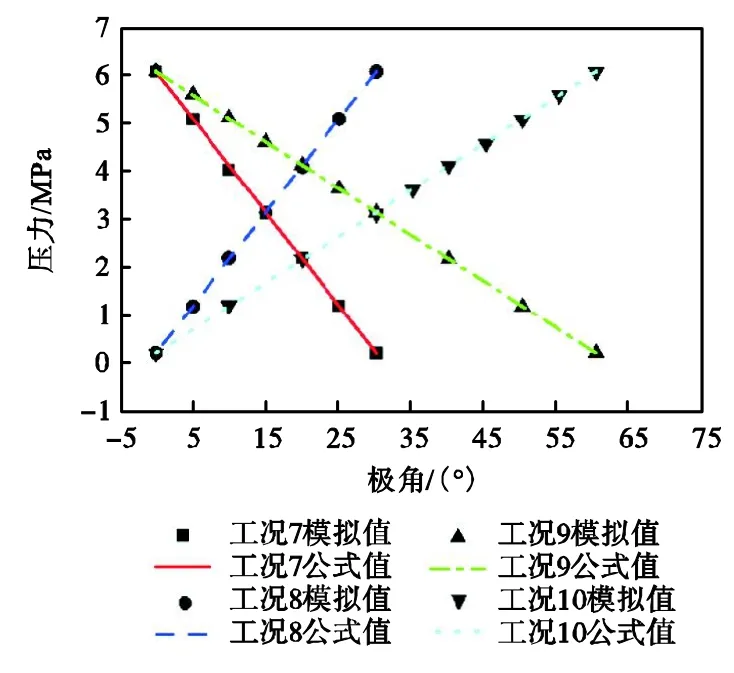
图8 端面周向泄漏时压力在周向上的分布Fig.8 Pressure variations in circumferential leakage on the end face

图9给出了工况11条件下通过CFD计算的周向泄漏过程的液膜压力分布云图.同样地，压力与极角之间也呈现着线性的关系规律，验证了本文对该过程中压力分布的假设.

图9 工况11下液膜的CFD压力云图展开图Fig.9 Developed CFD pressure cloud on the film of case 11

在图 10中，从压力随极角变化的分布曲线可以看出，解析模型与 CFD表现出相近的计算结果，并且这两者计算的压力分布曲线之间的相关系数大于99.99%.以上的结果能够充分证明本文所提出的计算模型能够对 RERD系统中所发生的主要泄漏过程压力分布规律进行准确表达.

图10 周面周向泄漏时压力的分布Fig.10 Pressure variations in circumferential leakage between the annular gaps

图11给出了不同工况条件下通过解析式和CFD两种计算方式所得到的泄漏流量的比较结果.由图可知，通过两种方法所计算得到的泄漏量的相对偏差表现为 5.08%～9.23%.从相对偏差的范围的宽度仅为4.15%的差距来看，这差距必然来自计算的偶然误差.鉴于图 11中的解析公式值与图 6相同，仍一定程度低于 CFD计算结果，这意味着在泄漏过程中泄漏边界上所发生的端部效应不能忽略，这一因素尽管对压力分布影响并不显著，但显然是影响泄漏流量的关键因素.综合图 6和图 11中的数据可以发现，泄漏过程中液膜厚度、径向密封距离等物理参数的改变均不会影响本文的泄漏解析模型的准确性.

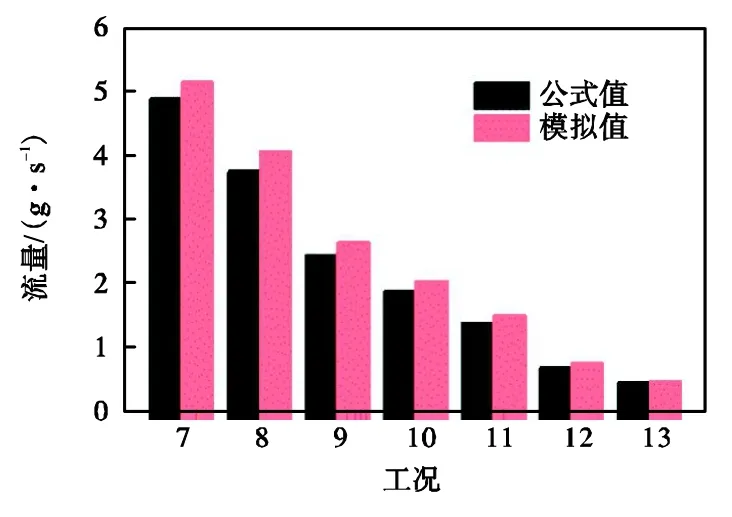
图11 周向泄漏时的泄漏量计算值Fig.11 Calculated leakage in the circumferentially leaking process

鉴于模型对独立状态下的不同流动形式均能准确表达，因此也必然能对 RERD环境中各路径区域内仍表现为典型流动形式的大部分区域准确表达.

为了验证解析模型对 RERD装置中所有区域泄漏规律表达的准确性，本文按照表1所给出的工况条件对RERD装置的总泄漏量进行了计算.结果表明，解析模型计算得到的装置内部总泄漏量为 23.16g/s，与相同工况下CFD计算得到的24.34g/s的结果非常相近，且相近度高达 94.90%.因此可以推断，在海水淡化系统中 RERD的操作条件和与之具有相同数量级的其他操作条件相比，解析模型能对 RERD的总泄漏量准确描述.

对于表1的条件所描述的RERD而言，路径1、2、3在液膜厚度均为 0.02mm时流量占比分别为75.505%、17.895%、6.600%.显然，路径 1的流量占最大比例，并远大于其他路径.这意味着端面径向泄漏是RERD中内部泄漏发生的主要路径.

5 结 论

(1)本文提出了一种以端面径向泄漏、端面周向泄漏和周面周向泄漏 3种主要泄漏路径为基础的RERD中泄漏过程的解析计算模型.

(2)本文的解析计算模型对表达 3种泄漏过程规律均表现了较高的准确性，对压力分布曲线的预测相对系数高于 99.99%，对流量计算的平均偏差为7.23%，对 RERD装置总泄漏量的预测相近度为94.90%.

(3)相同配合间隙条件下，端面径向泄漏路径上的泄漏流量占装置总泄漏量的比例最大，为75.505%；端面周向泄漏和周面周向泄漏占比分别为17.895%和6.600%.