基于多粒度时间注意力RNN的航班客座率预测
邓玉婧,武志昊,林友芳
(北京交通大学 计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室,北京 100044)
0 概述
21世纪以来,我国民航客运业务得到迅速发展。中国民用航空局发布的《2017年民航行业发展统计公报》[1]显示,2013年—2017年,我国民航旅客运输量从3.54亿人次增加到5.52亿人次,提高了55.93%,年均增长率达到11.5%。随着民航旅客量的迅速增长,航空客运需求预测越来越受到航空公司、机票代理商、飞机制造商等相关企业的关注。航空客运量需求预测包括航线客运量需求预测、机场客运量需求预测、航空公司市场份额预测和航班客运量需求预测等[2],其中,航班客运量需求预测是较细粒度上的需求预测,是航空座位优化控制和差别定价的基础。
对航空客运市场而言,航班客座率是衡量航班客运量需求的一个重要指标。航空公司通过航班客座率来衡量运力与运量是否匹配,并处理一系列衍生问题,包括溢出、虚耗、超售等。飞机制造商也需要关注客座率,它是判断航空公司是否需要增加运力,是否需要引进飞机的一个重要指标[3]。
民航航班客座率预测是一项极具挑战性的工作,其受诸多复杂因素的影响,例如多粒度时间相关性、航班自身属性相关性和外部因素相关性等。多粒度时间相关性包括起飞时刻相关性和起飞日相关性。其中,起飞时刻相关性是指给定某一航线,其某一起飞日中不同起飞时刻的航班客座率之间相互影响,且起飞时刻越接近的航班,客座率也越接近,起飞日相关性是指航班自身的客座率数据在时间维度上呈现趋势性和周期性。航班自身属性相关性是指航班客座率会受到机型、航空公司、座位数等自身属性的影响。外部因素相关性是指节假日、天气、突发事件和高铁的开设等因素对航班客座率产生的影响。航班客座率预测的关键是全面合理地考虑各种因素的影响。
本文通过构建基于多粒度时间注意力机制的循环神经网络模型(Multi-Time level Attention Recurrent Neural Network,MTA-RNN),提高航班客座率预测准确性。依据时间粒度构建多级注意力机制,利用基于航班起飞时刻的注意力机制捕获预测航班与其所在航线上其他航班的客座率时间序列之间的相关性,同时应用起飞日注意力机制捕获预测航班客座率时间序列自身的趋势性及周期性。在此基础上,设计一个通用的外部因素融合模块,对航班自身属性和节假日等其他因素进行整合,并将其引入多粒度时间注意力机制网络模型中,以提高航班客座率预测的准确性。
1 相关工作
民航航班客座率预测在本质上是一个时间序列预测问题。在早期,交通领域的预测问题多采用传统的时间序列预测方法,其基本模型是自回归滑动平均(Auto-Regressive Moving Average,ARMA)模型[4]。基于该模型的各种变体,如向量自回归(Vector Auto-Regression,VAR)模型[5]、自回归积分滑动平均模型(Auto-Regressive Integrated Moving Average,ARIMA)模型[6]、季节ARIMA[7]等被广泛应用于不同的研究领域。上述方法能够较好地捕获时间序列数据的时间相关性,但不能捕捉非线性关系以及外生时间序列对目标时间序列的影响。
为解决以上问题,各种非线性自回归(Nonlinear Auto-Regressive exogenous,NARX)模型[8]得到快速发展,其中许多方法被应用于交通领域的预测问题,如人工神经网络(Artificial Neural Network,ANNs)法[9]和基于径向基函数(Radial Basis Function,RBF)的支持向量回归算法[10]等。尽管这些方法在交通领域预测问题上已取得实质性进展,但其大多数使用一个预定义的非线性形式导致无法适当地捕捉潜在的非线性关系。
近年来,由于深度神经网络强大的表示能力,基于深度学习的方法被广泛应用于交通预测问题中。其中,循环神经网络(Recurrent Neural Network,RNN)[11]是一种专为序列建模而设计的深度神经网络,由于其能够灵活地捕获非线性关系,该模型受到广泛关注,尤其在NARX时间序列预测上表现出色[12]。然而,传统的RNN存在梯度消失问题[13],不能很好地捕获长时间的依赖。为解决此问题,之后又相继提出长短期记忆网络(Long Short-Term Memory,LSTM)和门控循环单元(Gated Recurrent Unit,GRU)[14],这两种方法被广泛应用于机器翻译、语音识别、图像处理等领域[15-17]。近两年,RNN方法被大量应用于时间序列的研究中,例如编解码网络[14]和基于注意力机制的编码器网络[15]等。
基于LSTM或GRU单元的编解码网络因其在机器翻译上的成功应用受到广泛关注,其主要思想是通过固定长度的向量编码原句,然后使用解码器生成对应翻译。但是,随着输入序列长度的增加,编解码网络的性能会迅速下降[18],而时间序列预测问题通常基于目标及相关时间序列中相对较长的部分进行预测。为解决这一问题,研究人员提出基于注意力的编解码网络,通过注意力机制选择编码器所有时间步上的部分隐藏状态。文献[19]提出双阶段注意力循环神经网络模型DA-RNN,以解决具有多个外生序列的目标时间序列预测问题,且该模型的性能优于很多传统时间序列预测方法和基于深度学习的基本方法,DA-RNN模型不仅可以自适应地选择最相关的外生序列输入特征,还可以适当捕获时间序列的长期依赖性。文献[20]基于DA-RNN的思想,结合地理传感器数据的时空相关性,提出针对地理传感器数据的多阶段注意力网络模型GeoMAN,以解决城市空气质量预测问题。尽管DA-RNN模型能够有效预测具有多个外生序列的目标时间序列,但该模型并不完全适用于航班客座率预测。这是因为DA-RNN模型虽然考虑了多个外生序列对目标时间序列的影响,但这些外生序列是平铺并列的关系,而在航班客座率预测问题中,多个外生序列(即同一航线中的所有起飞时刻的航班客座率构成的时间序列)之间存在时序关系,DA-RNN模型不能捕获其时序依赖性。为解决上述问题,本文利用MTA-RNN模型进行航班客座率预测。该模型通过多级注意力机制获取航班客座率在不同时间粒度下的时序相关性,在编码器中加入一个LSTM单元,以捕获航班所在航线中不同航班的客座率间的时序依赖性,并通过外部因素融合模块同时考虑航班自身属性和节假日等其他因素对预测航班客座率的影响。
2 形式化表示与问题定义
2.1 形式化表示

2.2 问题定义
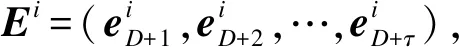
3 MTA-RNN模型
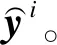
1)多粒度时间注意力机制。它由分别结合起飞时刻注意力机制和起飞日注意力机制的2个编码器组成。在编码器中,采用2个独立的LSTM单元,其中,编码器部分的第2个LSTM单元用来捕获预测航班所在航线中不同航班客座率的时序依赖性。在此基础上,引入起飞时刻的注意力机制,通过参考第1个LSTM单元先前隐藏层的状态值和第2个LSTM单元在各起飞时刻的状态输出值,自适应地捕获每个起飞日其他起飞时刻的航班客座率对预测航班客座率的影响。在解码器中引入起飞日注意力机制,以自适应地选择预测航班起飞日级别的状态输出值,从而捕获预测航班客座率时间序列的自身趋势性和周期性。
2)融合外部因素的模块。该模块用于处理航班自身属性和节假日等其他因素对预测航班客座率的影响,其输出作为部分输入提供给解码器。
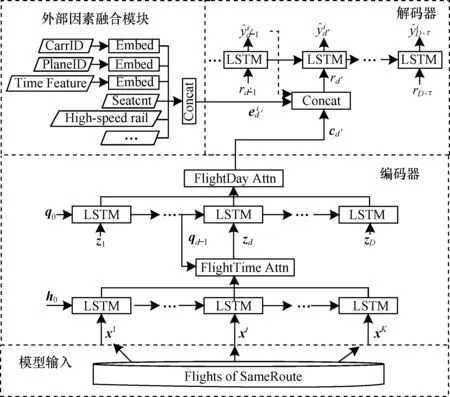
图1 MTA-RNN模型架构Fig.1 Architecture of the MTA-RNN model
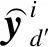
3.1 多粒度时间注意力机制
3.1.1 结合起飞时刻注意力机制的编码器

由航班客座率的起飞时刻相关性可知,不同起飞时刻的航班每日的客座率构成的时间序列存在复杂的相关性。与20:00的航班相比,起飞时刻为8:00的航班与9:00的航班客座率曲线的变化趋势更接近 。为了能够自适应地捕获目标序列和其他起飞时刻航班每日客座率构成的时间序列相关性,针对编码器第2个LSTM单元在t起飞时刻输出的隐藏层状态值ht,采用如下的起飞时刻注意力机制进行运算:
(1)
(2)

(3)
编码器中第1个LSTM单元在起飞日d的隐藏层状态值输出如下:
qd=fea(qd-1,zd)
(4)
其中,fea是编码器第1个LSTM单元的更新函数。通过本文的起飞时刻注意力机制,编码器第1个LSTM单元可以选择性地关注编码器第2个LSTM单元在某些起飞时刻的隐藏层状态值,而不是平等地处理所有起飞时刻的隐藏层状态值。
3.1.2 结合起飞日注意力机制的解码器
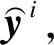
(5)
(6)
(7)

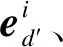
(8)
其中,fd表示解码器中LSTM单元的更新函数。将上下文向量cd′与隐藏层状态gd′进行向量拼接,得到的新隐藏层状态用于最终预测,计算过程如下:
(9)

3.2 外部因素融合
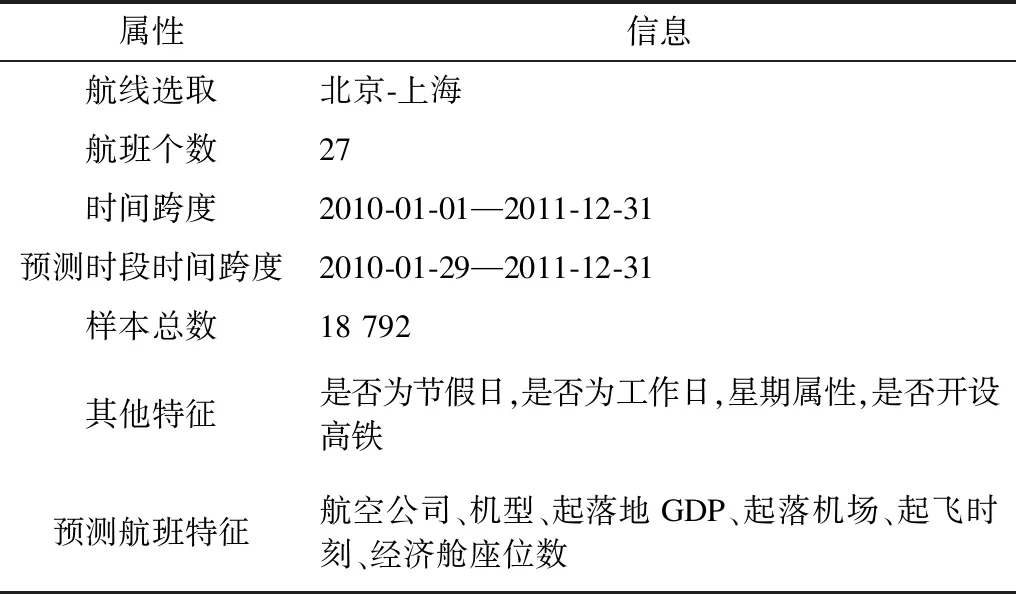
航班客座率受航班自身属性和节假日等其他因素的影响,文献[20]针对这些外部因素的影响进行研究。本文设计了一个简单有效的模块对外部因素进行融合,提出MTA-RNN模型。
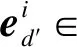
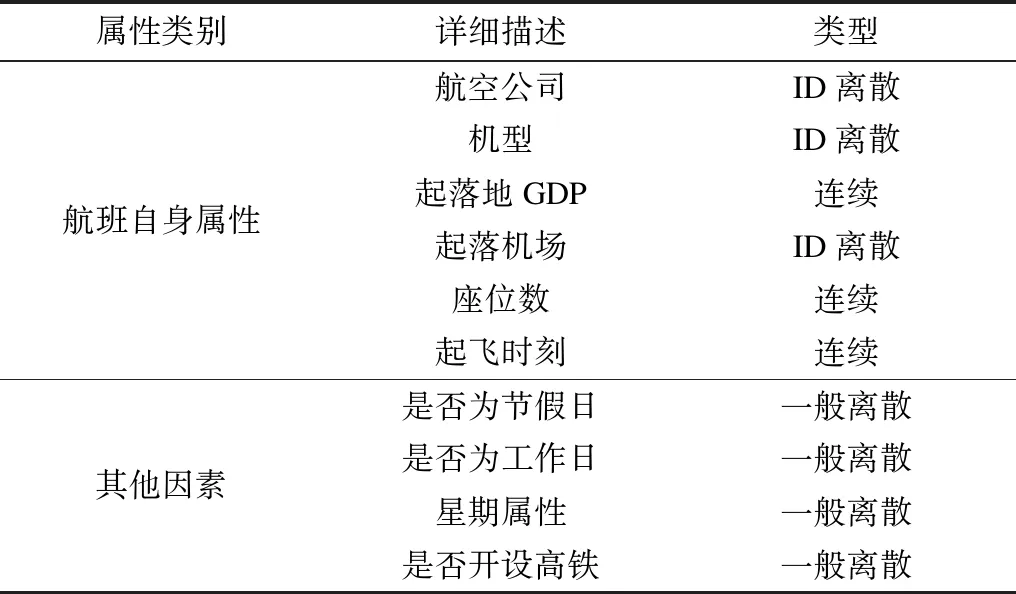
表1 外部因素信息Table 1 Information of external factors
3.3 模型训练
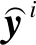
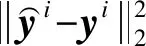
(10)
其中,θ表示MTA-RNN模型中所有需要学习的参数,即第3.1节中提到的We、Wl、Ue和Ul等。
MTA-RNN模型的训练过程如算法1所示。其中,第1行~第11行介绍了将原始数据转换成模型所需输入样本的过程,第12行初始化模型参数,第13行~第16行根据训练集迭代训练模型,直至满足停止条件。
算法1MTA-RNN训练算法

输出MTA-RNN模型合适的参数
//构造训练实例
1.∅→S;
2.for 待预测航班起飞时刻i(1≤i≤K) do{
3.for 可预测的起飞日h(D 4.//xh表示在起飞日h航线上所有起飞时刻航班的客座率构成的向量 5.x=[xh-D,…,xh-2,xh-1]; 7.//Vi表示需要预测的目标航班未来τ天的客座率构成的向量 9.将样本({x,ei},yi)加入训练集S 10.} 11.} //模型训练 12.初始化MTA-RNN中所有可学习的参数θ 艺术绘画中的肌理是一种特殊的语言表达形式,是艺术家在艺术作品的创新中所使用的一种表达途径。艺术家认为肌理已经不单单只是在艺术作品中简单浮现出的一种纹路,它也可以表达作者的内心感情。因此他们将肌理效果广泛运用到绘画作品当中,通过绘画作品中的肌理制作来体现艺术家内心深处的思想感情。 13.repeat 14.从S中随机选择一批训练实例Sbatch 15.用Sbatch寻找最优参数θ并最小化式(10) 16.Until 满足停止条件 本文在中国航信提供的真实历史航班客座率数据集上进行实验,将MTA-RNN模型与其他3种基准方法进行对比,以证明该模型在航班客座率预测问题上的有效性。 本文使用的是民航2010年—2011年的历史航班客座率数据,通过对数据进行预处理,获得实验所需属性,主要包括航班(即航空公司、航班号、出发地、到达地)、起飞日期、起飞时间、机型、座位数、起落地GDP、各舱位等级航班客座率,选取北京-上海航线在两年内起飞日达584(730×89%)天以上的航班数据作为实验数据集,时间窗口长度D=28、预测天数τ=7,则统计信息如表2所示。 表2 数据集统计信息Table 2 Statistics of the dataset 本文按照时间顺序将数据集划分为非重叠的训练集、验证集和测试集,划分比例为8∶1∶1,在实验数据集中选取27个航班,将预测时段为2010-01-29—2011-08-09(共557天)的经济舱客座率数据作为训练集,将预测时段为2011-08-10—2011-10-18(共70天)的数据作为验证集,其余数据作为测试集。假定h代表需要预测的目标航班未来τ天中的第1天,则预测时段为[h,h+τ-1],该航线上所有起飞时刻航班的历史客座率数据时段为[h-D,h-1],依据以上时段划分构造单个数据样本,按照每天一次滑动构建新的预测时段,通过上述操作,每一个航班可以构建696个样本,总样本数为27×696=18 792。 在进行模型训练之前,对数据进行预处理是非常必要的,由于航班客座率取值范围为[0,1],因此无需对其进行归一化。对于外部输入数据,本文采用One-Hot编码方式分别对起飞日期的星期属性,是否工作日、节假日,航空公司机型,起落机场,所在航线是否开设高铁等离散特征进行编码,对于起落地GDP、起飞时刻、经济舱座位数等连续特征本文采用min-max归一化方法归一到[0,1]之间,归一化的具体过程如下: (11) 其中,x表示原数据,x′表示数据在[0,1]之间新的表示,minx、maxx分别表示原数据中的最小值和最大值。 本文将MTA-RNN模型与以下3种基准模型进行对比: 1)ARIMA模型:是一个著名的时间序列预测方法,常用于预测现实生活中的非平稳时间序列。 2)LSTM模型:LSTM是一种循环神经网络,通过改进神经元结构,在训练长时间序列时缓解反向传播过程中的梯度消失问题。本文使用7个不同的LSTM单元分别预测航班未来7天的客座率。 3)Seq2seq模型:使用一个RNN将输入序列编码为特征表示,并通过另一个RNN迭代进行预测。 本文实验平台如下:GPU选用TITAN Xp,CPU选用Intel Xeon,模型框架选用TensorFlow。对于ARIMA模型,本文选取前28天的航班客座率作为输入,模型参数调至最优,LSTM模型、Seq2seq模型与MTA-RNN模型类似,选用预测航班历史D={7,14,28,42,56}天的经济舱客座率信息作为模型输入,通过验证不同的超参选择每种基准模型的最优超参。 本文采用平均绝对误差(MAE)和均方根误差(RMSE)作为模型预测效果的评价指标,计算公式如下: (12) (13) 在模型训练阶段,批大小(Batch Size)设为256,学习率为0.000 1,训练轮数为500,并采用早停策略防止过拟合。在MTA-RNN模型中,有4个需要调节的超参,分别是时间窗口长度D,编码器中2个LSTM单元的隐藏层维度n、m,解码器隐藏层维度p。本文令D={7,14,28,42,56},在其上进行网格搜索以得到最优取值。为了简便起见,本文在编解码器LSTM单元中使用相同的隐藏层维度,在该参数上进行网格搜索n=m=p∈{32,64,128,256},此外,本文采用堆叠LSTM(层数记为f)作为编解码器的单元来提高模型性能。实验表明,D=28,n=m=p=64,f=2的超参设置会得到较好的预测效果。 为了进一步研究每个模型组件的有效性,本文将MTA-RNN模型与以下3种变体进行比较: 1)MTA-RNN-nExternal模型:此变体不考虑外部因素对航班客座率的影响,即无外部因子融合模块。 2)MTA-RNN-nFTAttention模型:此变体不包含起飞时刻注意力机制。 3)MTA-RNN-nFDAttention模型:此变体不包含起飞日注意力机制。 本文涉及的实验均是预测航班未来7天的航班客座率。 4.5.1 外部因子融合模块评估 外部因子融合模块作为模型的一个实用组件可提供额外的信息,以提高预测性能。MTA-RNN模型与其3种变体预测未来7天航班经济舱客座率的结果对比如图2所示,可以看出,MTA-RNN模型的预测效果明显优于去除外部因素融合模块的MTA-RNN-nExternal模型,这是因为外部因素融合模块能使MTA-RNN模型在未来的时间步中考虑到航班自身属性及其他因素对预测航班经济舱客座率的影响。 图2 4种模型对未来7天航班客座率的预测性能对比Fig.2 Comparison of passenger load factor prediction performance in the next 7 days between 4 models 4.5.2 起飞时刻注意力机制评估 图3给出3种模型在预测未来7天航班客座率时每天的预测效果对比。由图3可以看出,MTA-RNN模型优于去除起飞时刻注意力机制的MTA-RNN-nFTAttention模型,由此可见,考虑不同起飞时刻航班客座率对预测航班客座率的影响可有效提高预测准确率。 4.5.3 起飞日注意力机制评估 本文在解码器中结合起飞日注意力机制,选择编码器第1个LSTM单元中不同时间步的隐藏层状态值来对目标航班客座率进行预测,通过尝试不同的时间窗口D验证起飞日注意力机制的有效性。图4给出4种模型的预测性能随时间窗口的变化情况。由图4可以看出, 当D=28时,MTA-RNN模型及其3种变体都达到最小误差值,当D很大时,4种模型的性能均会迅速下降,这是因为某起飞时刻的航班自身经济舱客座率时间序列没有这么长的时序依赖性。同时,由图4可知,MTA-RNN模型比MTA-RNN-nFDAttention模型表现更优,因为起飞日注意力机制增强了长期预测性能。 图4 4种模型预测性能随时间窗口的变化曲线Fig.4 Curve of prediction performance of 4 models varying with time window 将本文的MTA-RNN模型与其他3种基准模型进行对比。为公平起见,每种模型均将其参数调至最优以便呈现其最佳性能,预测效果对比如表3所示。由表3可知,MTA-RNN模型在RMSE、MAE两个评价指标上均明显优于其他3种方法。 表3 4种模型未来7天总体预测性能对比Table 3 Comparison of overall prediction performance in the next 7 days between 4 models 图5 MTA-RNN模型与3种基准模型每天的预测性能对比Fig.5 Comparison of daily prediction performance between the MTA-RNN model and 3 benchmark models 本文构建了一种基于多粒度时间注意力机制的循环神经网络模型MTA-RNN,用以提高民航领域航班客座率预测的准确性。依据时间粒度构建起飞时刻注意力机制和起飞日注意力机制,通过两级注意力机制的结合,获取航班客座率在不同时间粒度下的时序相关性,并通过外部因素融合模块考虑航班自身属性及节假日等外部因素的影响。在中国航信提供的真实历史航班客座率数据集上的实验结果表明,MTA-RNN模型的预测准确率高于ARIMA模型、LSTM模型和Seq2seq模型。下一步将把该模型应用于时间跨度更大的航班客座率预测问题中,并通过获取更多维度的数据,如天气、机票价格等来改善模型的预测性能。4 实验结果与分析
4.1 数据集
4.2 数据预处理
4.3 基准模型与评价指标
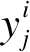
4.4 超参选取
4.5 MTA-RNN模型与其变体的对比
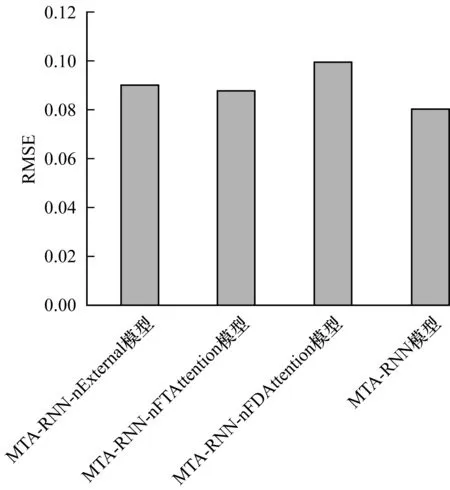
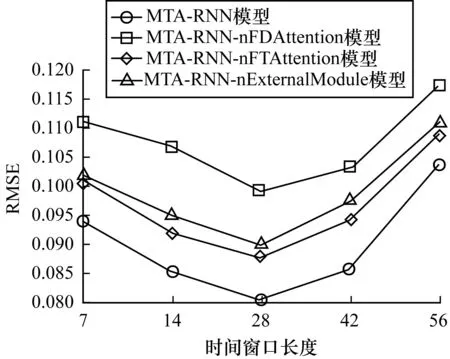
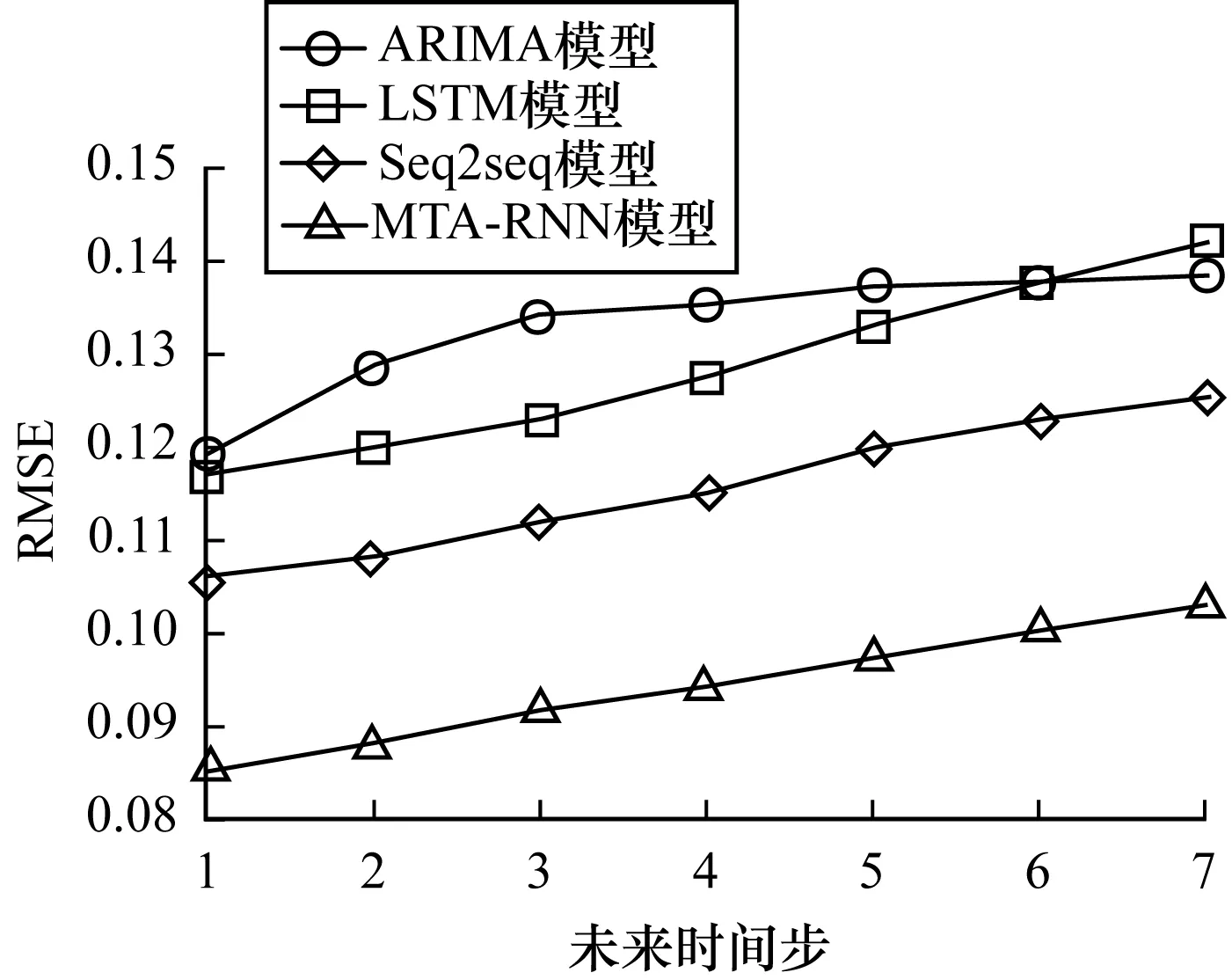
4.6 MTA-RNN模型与其他3种基准模型的对比
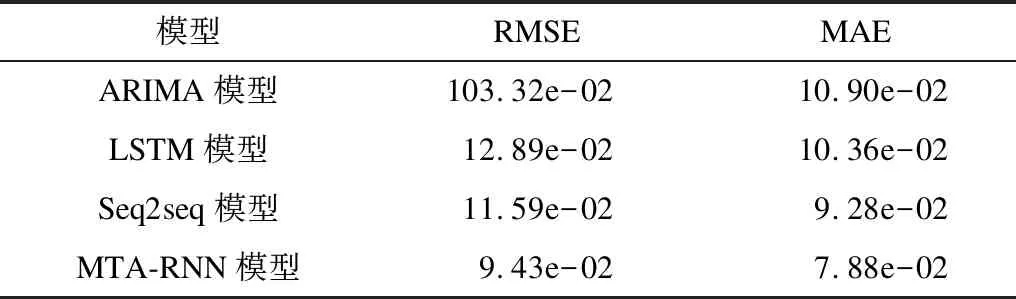
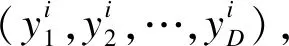
5 结束语

