TLP:一个动态网络中的时序链路预测算法

符汉杰,熊 赟,朱扬勇

(1.复旦大学 计算机科学技术学院,上海 200433; 2.上海市数据科学重点实验室,上海 200433;3.上海先进通信与数据科学研究院,上海 200433)

0 概述

在现实世界的网络中,如社交网络、基因网络,用户、基因等表示为网络中的节点,而用户间的朋友关系、基因间的相关性表示为节点间的连接关系。链路预测是网络中的一个重要应用,即通过已知的网络节点及其节点间的连接预测对未连边的2个节点间存在连边的可能性,其在用户推荐[1]、基因序列分析[2]等场景中有着广泛的应用和重要的价值。现有网络上的主要研究是基于静态网络上的算法,如随机游走优化的Node2vec[3]、矩阵分解的HOPE[4]和深度自编码器的SDNE[5]。

而实际中的网络具有丰富的动态特性,网络中节点之间的连接随着时间的推移[6-7],会产生新的联系或者终止连接,从而导致网络结构发生变化以及节点中内在的偏向发生偏移。网络的演化原因是多方面的,如社交网络中随着用户的偏好变化影响到社区聚合或分离,用户购买商品随着时间长短呈现周期性变化的规律。单纯地考虑网络的整体信息,忽略其历史动态演变过程,难以预测有动态特性的数据及其时序上的规律。通过研究网络结构随时间变化的演变过程,预测节点间未来连接的可能性变化,以及分析未来社区演化的规律,更有利于提高链路的预测精度。

动态网络中的链路预测需要结合网络的空间结构和时序演变的信息,考虑节点间的动态邻接信息,以提高链路预测的精确性,如TNE[8]和LIST[9]在动态图中考虑了节点间的一阶邻近信息,但高阶邻近信息的缺失使得模型的精度有所降低。网络中除了节点之间的直接连接关系,引入高阶邻近信息有助于表达网络的空间拓扑结构,例如,DPHE[10]通过静态网络的算法捕捉到网络中的高阶邻近信息,但其在不同时刻下独立的节点表示难以预测未来时刻的网络结构。

本文提出动态网络时序链路预测算法TLP(Temporal Link Prediction),来预测动态网络在空间上的高阶邻近信息以及时序上的演化规律。通过时序连接的方式将动态网络中不同时刻的静态网络相连,并且在网络上进行随机游走优化,得到节点的高阶邻近邻居以及鲁棒的节点映射向量来表示动态网络的空间结构信息。在此基础上，使用自回归的方式参数化节点向量,根据历史的节点状态推断下一时刻的节点向量，从而预测节点的时序演变规律,以生成未来时刻的网络结构。

1 相关工作

动态网络由于其动态演变的特性,在近年来的研究中得到越来越多的关注。静态网络的算法往往只关注于网络的历史连接方式,而忽略了连接的时序关系,如基于随机游走方式的DeepWalk[11]和Node2vec[3]、拟合高阶邻近的矩阵分解HOPE[4]、用深度自编码器的SDNE[5]等。因此,和动态网络的相关算法相比,静态网络算法不能很好地反映节点的偏好变化以及网络的结构演变。

在动态网络的相关研究中,有部分工作更关注历史网络的节点向量映射,而忽略了对未来网络的表达能力。如TNE算法[8]考虑相邻2个时刻的网络中,节点向量是上一时刻的向量加一个偏移,并且在特征空间中具有时序平滑的特性,因此,节点向量不会变化很大。而在DynamicTraid[12]算法中,也仅考虑了相邻2个时刻中3个节点之间的三角关系。在上述研究中,考虑相邻时刻中的节点向量差异为一个偏移向量,不同时刻下的偏移量是独立的,缺乏对动态网络中的时序演变规律进行刻画。和之前研究相比,LIST算法[9]使用多项式函数表达节点随时间变化的规律,因此针对更远时刻的网络能够刻画网络结构的时序性。但由于多项式的特性,节点向量往往取决于最高次项的系数,呈现单调性的变化，并且算法中只考虑了节点间的一阶临近信息,不能很好地捕捉网络的拓扑结构。DynGEM算法[13]使用深度自编码器的方式结合网络的一阶邻近和二阶邻近信息,DHPE算法[10]通过GSVD静态网络模型捕捉高阶邻近信息,DynGraphGAN算法[14]通过生成对抗网络的方式结合网络的高阶邻近信息和时序演变信息。上述算法每个时刻的节点向量表示是独立的。

TLP算法的主要目的是根据动态网络的历史结构生成基于时序特征的节点向量,不仅对已有的网络进行向量映射,而且通过捕捉整个网络的动态特性推断未来时刻下的节点向量。

本文算法的主要贡献如下:

1)TLP算法是一种有效的自回归动态网络节点向量表示,能够保留动态网络的时序演变特性。

2)TLP算法适用于大规模的网络,能够保留节点间的高阶邻近信息,维护动态网络的空间结构。

3)在几个真实数据集上与TNE、DHPE等算法对比,TLP算法性能具有明显提升。

2 问题定义

本文中的主要符号含义如表1所示。一个网络可以表达为G=(V,E),其中,V指网络的节点集合,E⊆V×V包含节点间的连接。本文考虑的网络是无权无向的,即对于每个连接的权重设定为1。

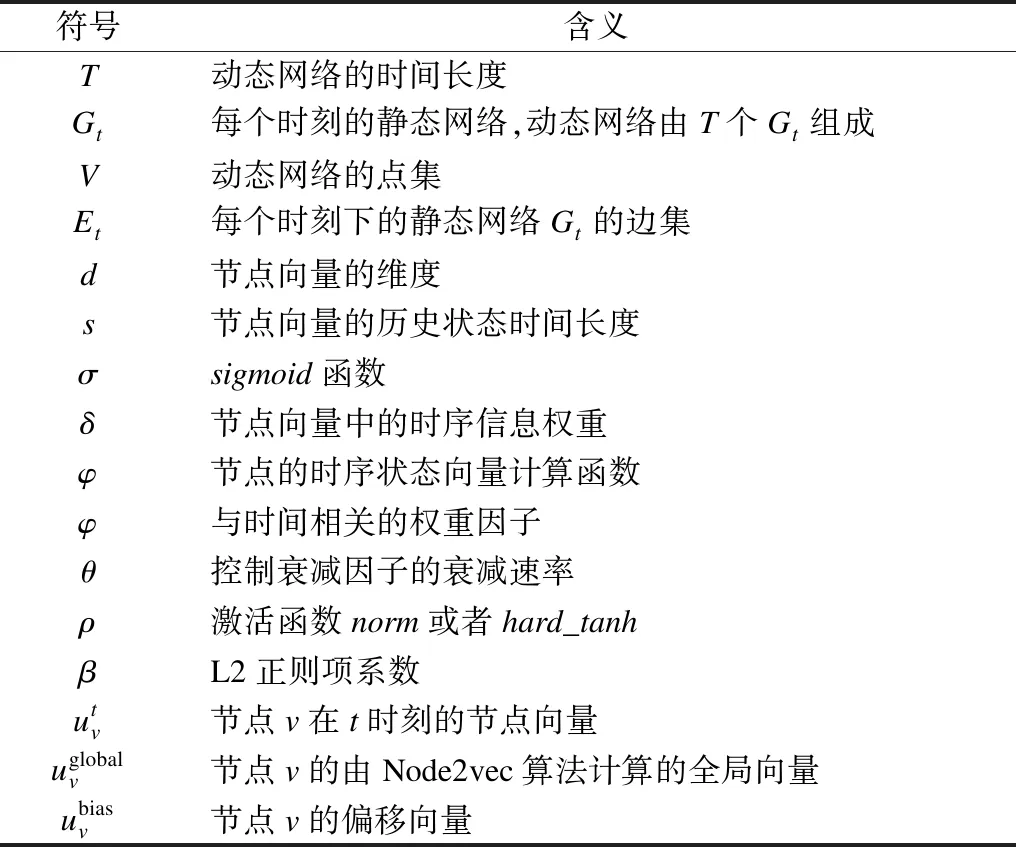
表1 符号及其含义

2.1 动态网络

一个动态网络可以看作是由T个静态网络{G1,G2,…,GT}组成,其中每个静态网络可表示为Gt=(V,Et),每个静态网络有着相同的节点集合,而边集随着时间变化发生演变。因此,对于动态网络中的每个节点可表示为(v,t),指代t时刻下的网络Gt中的节点v。相应的边可以表示为(u,v,t),指代t时刻下节点u和节点v中有一连边。

2.2 动态网络的时序链路预测

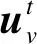
3 时序链路预测算法

本节介绍在动态网络上的链路预测算法TLP,算法的框架主要包括在动态网络上捕捉节点间的高阶邻近信息，通过自回归的向量表示和拟合网络随着时间演变的时序规律。

3.1 高阶邻近节点

与静态网络相比,在动态网络中，由于节点存在于不同时刻的静态网络中,因此节点间的关系除了考虑当前网络的连边,还需要结合不同时刻下与其他节点的连边信息,反映节点在不同时刻下的高阶邻近关系。

3.1.1 时序连接

定义不同时刻下节点的时序连接:假设t1≤t2,(v,t1)和(v,t2)中存在连边,当且仅当存在(v,v1,t1)∈Et1和(v,v2,t2)∈Et2,且不存在(v,v3,t3)∈Et3，t3∈(t1,t2)。在定义中,一个节点只与时间上最近的时序连接,使得节点与不同时刻下的其他节点按照时间的距离有序地连接。将节点在不同时刻的时序连接起来,使得动态网络中的各个子静态网络相互连接。

3.1.2 时序游走

一个可行的时序游走从节点(v1,t1)到节点(vk,tk),必定存在一个可行节点序列{(v1,t1),(v2,t2),…,(vk,tk)},所有的(vi,ti)与(vi+1,ti+1)之间有连边。因此,由游走路径上的连接信息可以得出,游走路径中的各个节点间在动态网络中是间接或直接邻近的。给定一个游走路径,可以采用Skip-Gram模型的形式,TLP算法的优化目标如式(1)所示。

(1)

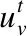
(2)

其中,φ(t′,ti-k,ti)是与时间相关的权重因子,表示在时间区间外的连接概率,会随着时间间隔增大权重因子变小。如社交网络中的朋友关系,陌生人间的关系可能会随时间变得更加亲密而成为朋友,朋友间的关系可能会随时间变得更加疏远而成为陌生人。具体的权重因子定义如下:

(3)

其中,参数θ是控制权重的衰减速率,当θ=0时,源节点与目标节点在动态网络中连接概率相等。

3.2 节点向量的时序表示

不同于静态网络的节点向量映射,设定动态网络的节点在不同时刻下映射到不同的向量,并且节点的向量映射函数是与时间独立的自回归函数。节点(v,t)的节点向量表达式如式(4)所示。

(4)

(5)

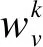
3.3 TLP算法

在动态网络中,由于网络的稀疏性[16],算法中每个节点使用自回归的向量映射方式容易产生过拟合的现象。因此,加入系数β的L2正则项提高模型的泛化能力。

在训练过程中,算法的优化使用Adam优化器,其中每批训练样本量的大小设置为1 024,初始的学习率为0.000 1,输出向量长度为50。本文的算法伪代码如算法1所示。

算法1TLP算法

输入动态网络{G1,G2,…,GT},时刻t

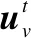
1.根据时序连接的定义,把动态网络转为静态网络G。

2.用Node2vec算法中的随机游走方式,得到游走路径集合walk。

3.LOOP

4.从游走路径walk中采样作为训练样本,路径上每个节点vi取窗口内的节点为正样本,通过负采样得到的节点vn～Pn(vi)作为负样本。

5.通过式(2)计算算法的损失函数。

7.重复步骤1～步骤3,直至算法收敛为止。

4 实验结果与分析

本节在公开的数据集上进行实验,通过几个基准的算法进行比较来评估算法的性能。

4.1 数据集

本文采用4个数据集进行实验,包括社交网络和共同作者关系网络。所有的网络都是无向无权重的动态网络,具体描述如下:

1)Facebook[17]、Epinions[18]、Digg[19]数据集:社交网络数据是从Facebook、Epinions和Digg中收集的，其中,网络中的节点表示用户,节点的连接在Facebook、Epinions数据集中表示用户的朋友关系,在Digg数据集中表示用户间的信任关系。用户间的关系有建立的时间,对此按照一个月的时间间隔划分数据集得到动态网络。对于时间缺失的连边,把它看作是第1个动态网络的初始边。

2)Dblp[20]数据集:共同作者关系网络反映的是在dblp computer science bibliography上的共同作者关系。网络中的节点表示论文作者,而节点间的连接表示作者共同发表论文，论文的发表时间作为连接的时间,以一年的时间间隔划分数据,保留不小于1970年的关系,从而得到最终的动态网络。

在4个真实数据上构造动态网络,节点数的范围为60 000～1 400 000,节点间连边数范围为700 000～8 500 000,动态网络的时间长度最大为48。具体的数据描述如表2所示。

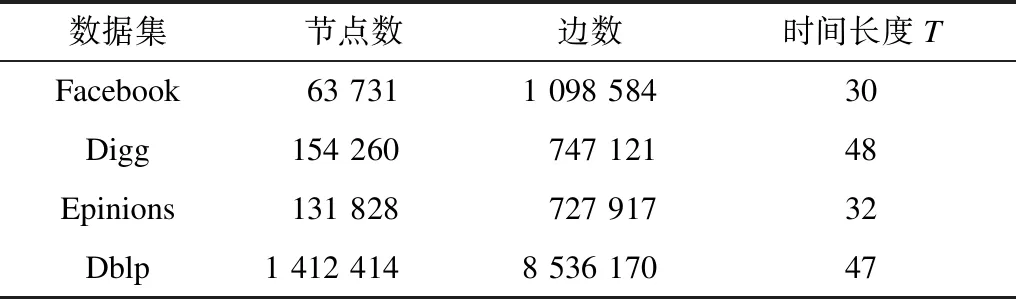
表2 具体数据说明

4.2 动态网络算法

为评估算法的性能,对目前有代表性的动态网络算法进行对比,具体如下:

TNE算法[8]:使用矩阵分解的方法将动态网络的节点映射到向量中,并且基于节点时序平滑的性质,考虑相邻时刻的同一节点向量的差异。由于算法只对每个历史时刻生成节点向量,因此采用T-5时刻下的节点向量作为未来时刻的结果。

DynamicTriad算法[12]:考虑相邻时刻下3个节点的三角闭合关系来捕捉网络中的结构信息和演化模式。与TNE算法类似,采用T-5时刻下的节点向量作为未来时刻的结果。

DHPE算法[10]:采用静态网络算法得到节点向量,然后根据网络的变化更新向量,实验中采用T-5时刻下的节点向量作为未来时刻的结果。

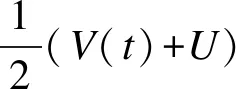
4.3 链路预测

在链路预测的任务中,使用动态网络中最后5个时刻的静态网络作为测试集,而其余的静态网络作为训练集。其中,测试集中的连边作为正样本,通过随机采样的方式得到与正样本同样数量的边集作为负样本。评估的指标采用AUC，所有实验运行的机器设备为220 GHz CPU,128 GB RAM和16 GB Tesla-P100 GPU,实验结果如图1～图4所示。

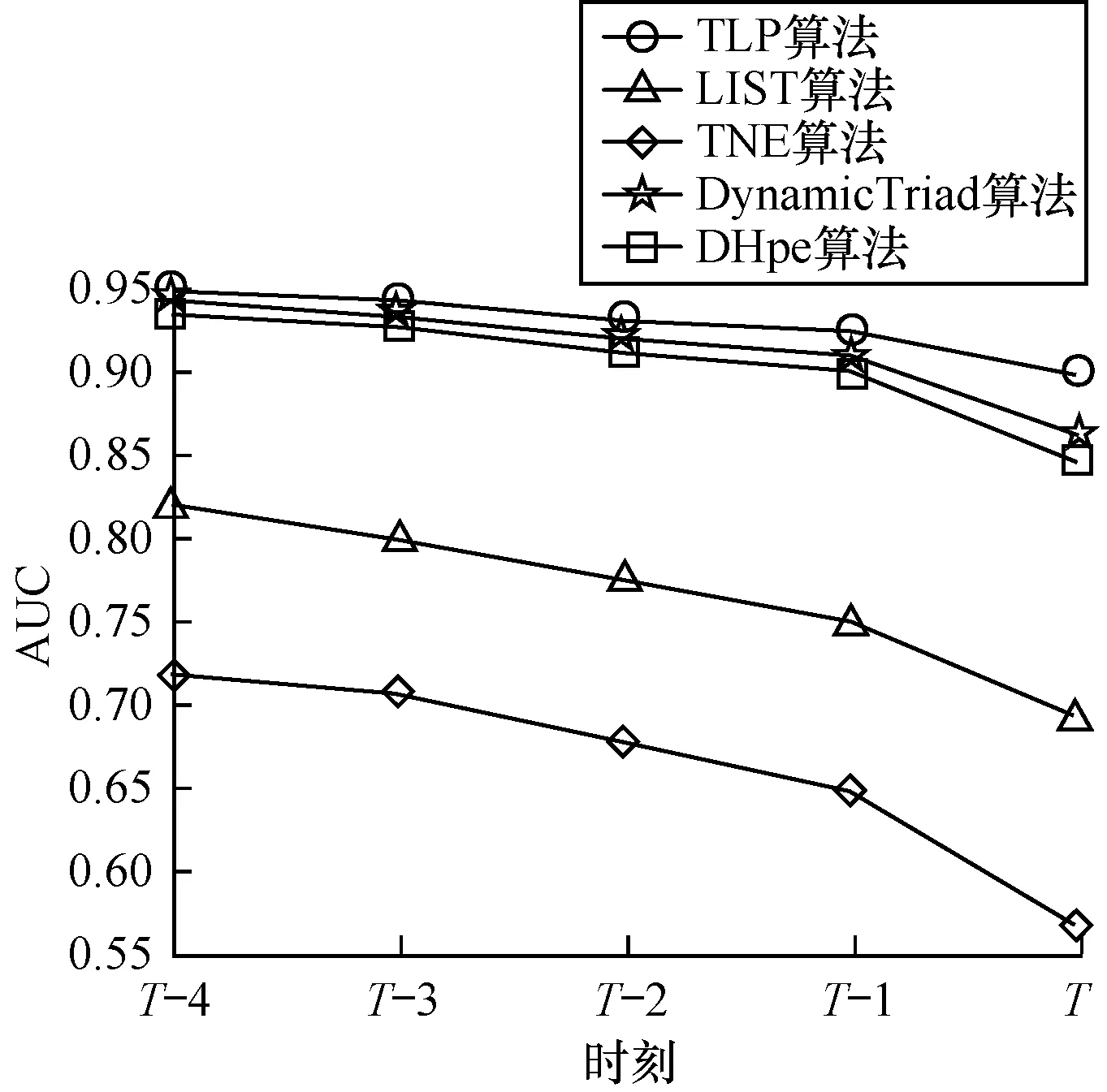
图1 Facebook数据集上AUC变化曲线比较结果

Fig.1Comparison results of AUC changing curve on Facebook dataset

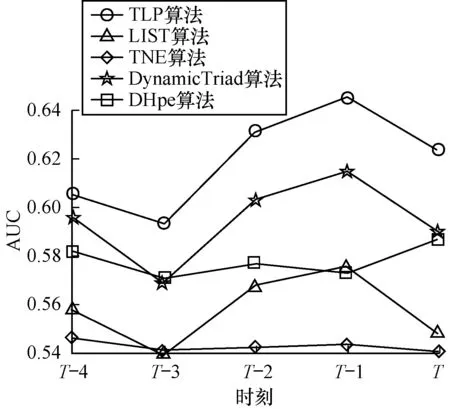
图2 Digg数据集上AUC变化曲线比较结果

Fig.2Comparison results of AUC changing curve on Digg dataset

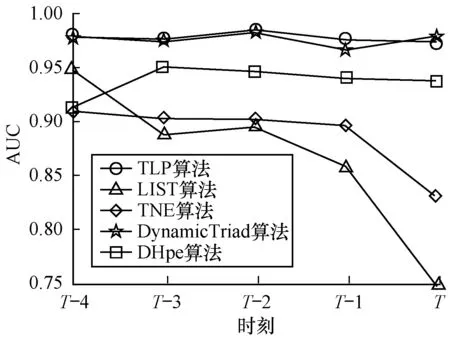
图3 Epinions数据集上AUC变化曲线比较结果

Fig.3Comparison results of AUC changing curve on Epinions dataset

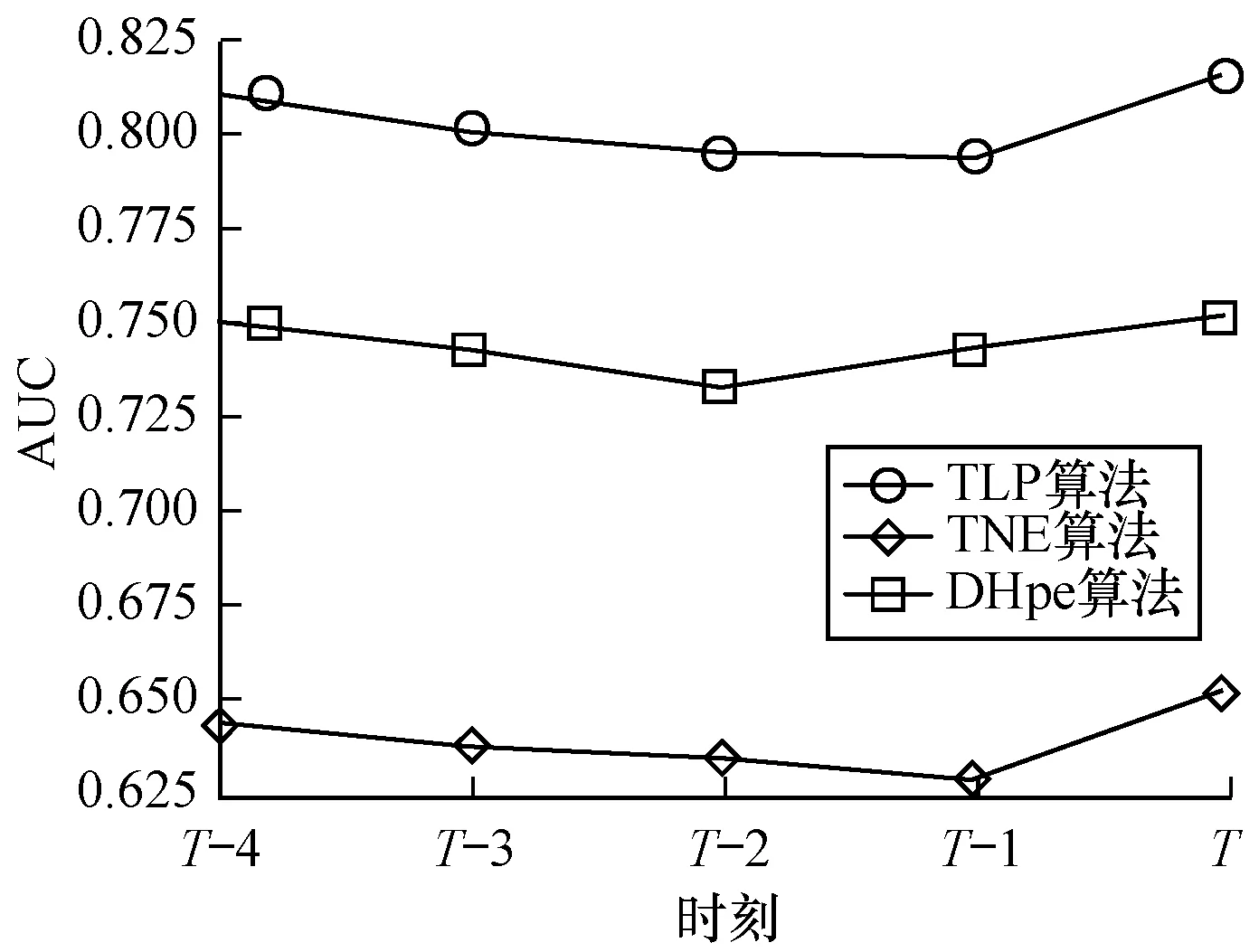
图4 Dblp数据集上AUC变化曲线比较结果

Fig.4Comparison results of AUC changing curve on Dblp dataset

根据上述实验结果可以得到以下结论:

1)TLP算法和TNE、LIST、DynamicTriad、DHpe算法相比,在各个数据集中的AUC指标都有提升,在Facebook、Digg、Epinions、Dblp数据集上的提升分别为1.72%、4.17%、0.13%和7.92%。因此,TLP算法在对未来时刻的链路预测任务中拥有更好的性能提升。

2)在Dblp数据集中,节点数量达到140万,在该大规模的网络中对算法的性能有比较高的要求。其中LIST算法受限于内存的限制,不适用于Dblp大大规模的数据集。而DynamicTriad算法受限于Tensorflow框架中张量的大小不能大于2 GB,也不能在Dblp数据集上运行。因此,图4中没有LIST和DynamicTriad算法的相关结果。而TLP算法采用随机游走的方式不需要输入整个网络进行优化,并且节点向量采用函数表达的方式需要的张量比DynamicTriad算法需求低,因此,能够适用于大规模的网络。

3)TNE算法的目的是把历史不同时刻的网络节点映射到低维的空间,但在数据集上的效果相比其他算法效果略低。由于TNE算法在T时刻的节点向量基于T-1时刻进行更新,容易陷入局部收敛的状态。并且算法中只考虑历史时刻的节点向量映射,并不能很好地反映未来时刻的节点向量变化。由于在实际网络中节点间的连边具有稀疏的性质,但算法中没有平衡正负样本的比例。使得结果稍差。

4)LIST算法使用多项式函数表达节点向量,向量随着时刻的增加呈指数式变化,与时序平滑的性质相违背。如在Facebook和Epinions数据集中,LIST算法在T时刻下的AUC指标较T-4时刻相比分别降低了0.13和0.20。而TLP算法在Facebook和Epinions数据集上的Auc指标分别降低0.05和0.01,比LIST算法中的多项式函数效果更优。并且LIST算法只考虑节点间的一阶邻近信息,不能很好地捕捉动态网络的拓扑结构。

5)DynamicTriad算法由于只考虑由历史时刻网络结构得到的节点向量,缺乏对时序演变规律的挖掘。而TLP算法能够考虑更高阶的邻近信息。因此，该算法在Facebook、Digg和Epinions数据集上的精度要低于TLP算法。

6)DHPE算法能够通过静态网络算法考虑高阶邻近信息,但由于其不能结合网络结构和时序信息,因此实验结果中该算法的精度有所降低。

4.4 参数分析

为证明TLP算法中参数的重要性,本文在Facebook数据集上根据不同的参数验证算法的效果。

在TLP算法中,参数δ可以平衡自回归节点向量表示中全局信息和时序信息的权重比,参数δ越大时序信息的权重比也越大。通过枚举参数δ来得到算法的结果,观测时序信息对节点向量的影响。本文枚举参数δ从0到1,固定参数d=50、s=2、β=0、θ=0。具体结果如图5示,可以看出，当δ=0.25时，TLP算法能得到最好的效果,而当δ=1时最差；当δ=0时,即TLP算法只考虑动态网络的全局信息而忽略了时序信息,在未来时刻的链路预测问题上依然能得到一个较好的效果,这反映出全局信息在动态网络中的重要性。而当δ=1时,加入了与全局信息等权重的时序信息,由于反映时序的参数个数与参数s成线性相关,优化过程中容易使时序信息权重比例过大导致效果降低。当δ=0.25时,由于能够平衡节点向量中的全局信息以及时序信息的权重比例,因此使得算法能够得到更好的效果。

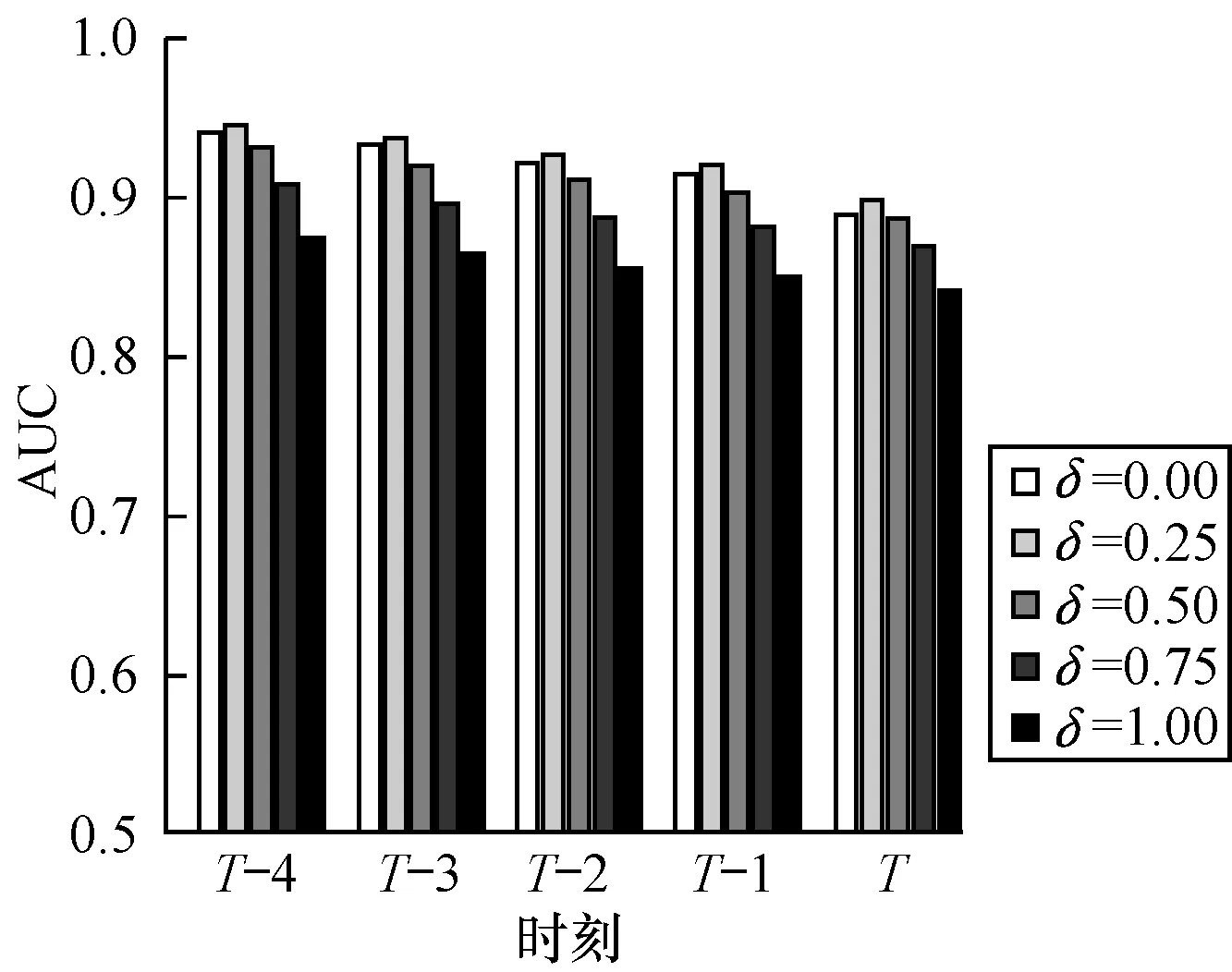
图5 δ参数在Facebook数据集中的验证效果

由于节点间关系会随时间发生衰减或增强,为了观测关系变化强度对算法的影响,通过枚举参数θ来得到算法的结果。参数θ越大,节点间关系变化越快。枚举参数θ从0到1,固定参数d=50、s=2、β=0、δ=0.25。具体结果如图6所示,可以看出，当θ=0.75时效果最好，当θ=0时,忽略了节点间的联系在时间上平滑过渡的性质，当θ=1时,节点之间连边的权重随时间变化衰减或者增长较快,使得算法效果较差。因此,选取适当的θ,控制节点间连边的权重变化,能够提升算法在动态网络上的效果。

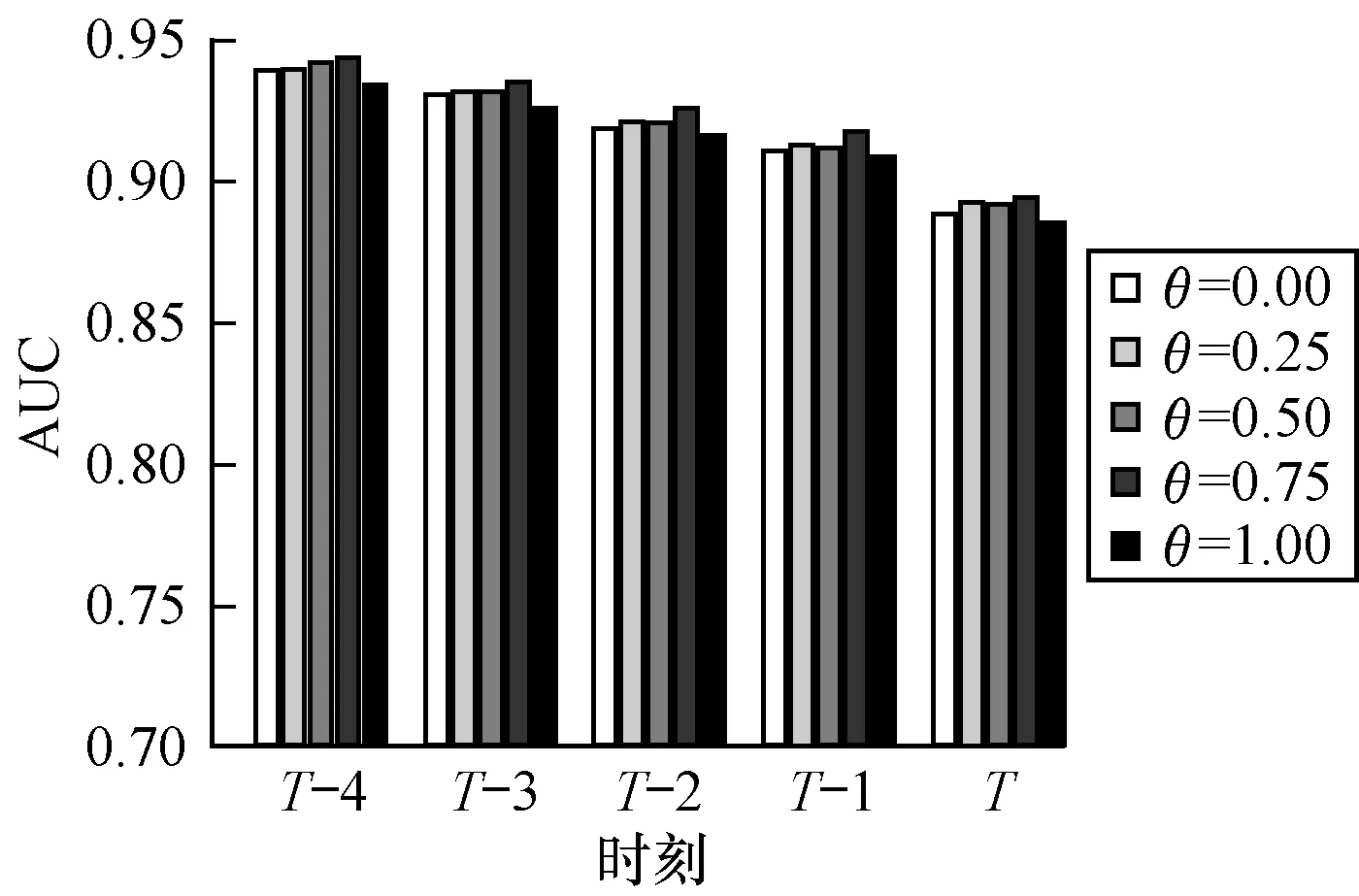
图6 θ参数在Facebook数据集中的验证效果

5 结束语

本文提出一个动态网络上的链路预测算法。该算法在时序连接的动态网络上寻找节点间的高阶邻近信息,可适用于大规模网络,同时节点运用自回归向量表示的方法捕捉节点向量与历史状态的关系，使用历史状态推导下一时刻的节点向量方式,解决了与时间相关的多项式向量表达中随时间增加向量表达性能降低的问题。在真实数据集上的实验结果表明,与现有动态网络相关算法相比,TLP算法在更远时刻网络上的链路预测任务中具有更高的精度。由于模型缺乏对内容属性的考虑,下一步将通过加入节点和连边的属性挖掘来提高模型的预测精确度。