基于GRNN的三元乙丙橡胶薄膜粘接界面力学性能参数反演*

刘应雷，高 波，姚 东

(1. 中国航天科技集团有限公司四院四十一所，西安 710025；2. 中国航天科技集团有限公司第四研究院，西安 710025)

0 引言

近年来，“飞马座”等火箭的吊耳结构存在吊耳和复合材料弹体之间的多层粘接界面；在挂飞过程中，粘接界面承受过载、冲击/振动等载荷，其结构完好性对导弹与飞机的安全性起着至关重要的作用[1-2]。固体火箭发动机中也存在大量粘接界面，如贴壁浇注式固体发动机中存在壳体/绝热层/衬层/推进剂的多界面结构，粘接界面的力学行为关系到发动机的结构完整性和可靠性[3-4]。因此，研究粘接界面的力学性能具有非常重要的意义。

自Hillerborg等[5]于1976年提出内聚力模型(Cohesive Zone Model，CZM)以来，其在模拟粘接界面的脱粘及断裂方面得到了广泛应用，如用于研究层合板的分层脱粘[6]、功能梯度材料的界面行为[7]及混合型断裂失效模式[8]等。内聚力模型的核心是采用牵引-分离关系(Traction-Separation Relationship，TS关系)来模拟粘接界面的脱粘，牵引-分离关系可有效表征粘接层的损伤失效过程[9]。Needleman[10]首先采用指数型内聚力模型对夹杂-基体界面脱粘过程中的孔洞形核过程进行了研究；Tvergaard[11]、Camacho[12]和Mi等[13-15]相继建立了梯形内聚力模型、线性软化的内聚力模型和双线型内聚力模型，其中以双线型内聚力模型应用最为广泛[16-18]。Freund[19]和Li[20]等认为，无论采用何种形式的内聚力模型表征粘接界面都必须考虑内聚强度和断裂韧性两个关键参数，这两个界面参数比内聚力模型的具体形状更为重要。

目前，主要通过拉伸、剪切和劈裂等实验确定粘接界面的力学性能参数[9]，通过单轴拉伸实验可确定内聚强度[21-26]，通过双悬臂梁(Double Cantilever Beam，DCB)[27-28]或双悬臂夹层梁(Double Cantilever Sandwich Beam，DCSB)[29-31]实验可确定断裂韧性，Davila[32]和Camanho[33]提出了确定双线性内聚力模型中初始刚度的不同方法。剪切效应、大位移效应、加载块和裂纹尖端旋转等因素会导致通过实验确定的界面参数与其准确值之间存在一定的偏差[21]。

为准确获取粘接界面的力学性能参数，周清春[25,31]等提出了一种包含了标准实验、数值仿真模拟、Hooke-Jeeves优化算法三大部分的反演分析方法；王娟[34]在建立正问题分析模型后，采用遗传算法对界面参数进行了反演求解。基于Hooke-Jeeves算法和遗传算法的反演方法经自主编程在统一平台下调用各类工程软件，尤其是迭代过程中调用有限元分析(Finite Element Analysis，FEA)，对大规模工程问题而言，单轮次FEA的耗时、不可预估的多轮次调用导致的反演周期是漫长的。

本文以文献[21]报道的试件及其界面参数为基础，经正交实验设计及对应的有限元计算结果，构造了FEA输出-内聚参数的数据样本，研究基于广义回归神经网络(General Regression Neural Network，GRNN)的内聚参数反演，为准确获取粘接界面的力学性能参数提供参考。

1 理论基础

1.1 双线性内聚力模型

牵引-分离关系的精确形状不会从根本上影响数值计算的结果[19-20]，因此本文选择采用双线性内聚力模型[22-23]。双线性内聚力模型中，与I型断裂对应的法向牵引-分离关系如图1所示，其控制方程为

(1)

其中

(2)

式中σ为牵引力；D为损伤因子；ft为内聚强度(抗拉强度极限)；w0为界面开始发生损伤时的法向分离位移；w为法向分离位移；w1为界面完全失效时的法向分离位移。

图1中牵引-分离关系曲线与坐标轴所围成区域面积大小为断裂韧性GIc。

图1 双线性内聚力模型的法向牵引-分离关系

在通过实验确定内聚强度ft和断裂韧性GIc后，确定双线性内聚力模型的牵引-分离关系还需要确定初始刚度(也称为“罚刚度”)K。界面的初始刚度无法通过实验直接确定，为确定K的值，引入位移系数d描述w0和w1之间的关系：

(3)

因此，

(4)

1.2 广义回归神经网络

广义回归神经网络(GRNN)[35-37]的理论基础是非线性回归分析。当GRNN中输入向量和输出向量的联合概率密度函数为高斯核函数时，与输入向量X对应的输出向量估计值为

(5)

式中n为训练样本的数量；Xi、Yi(i=1,2,…,n)分别为第i个训练样本的输入和输出；k为平滑参数。

根据式(5)可构造包含输入层、模式层、求和层和输出层的GRNN结构，如图2所示。网络的输入向量和输出向量分别为X=[x1,x2,…,xm]T和Y=[y1,y2,…,yl]T，其中m和l分别为输入向量和输出向量的维数。图2中其余各参数的具体含义见文献[35]。

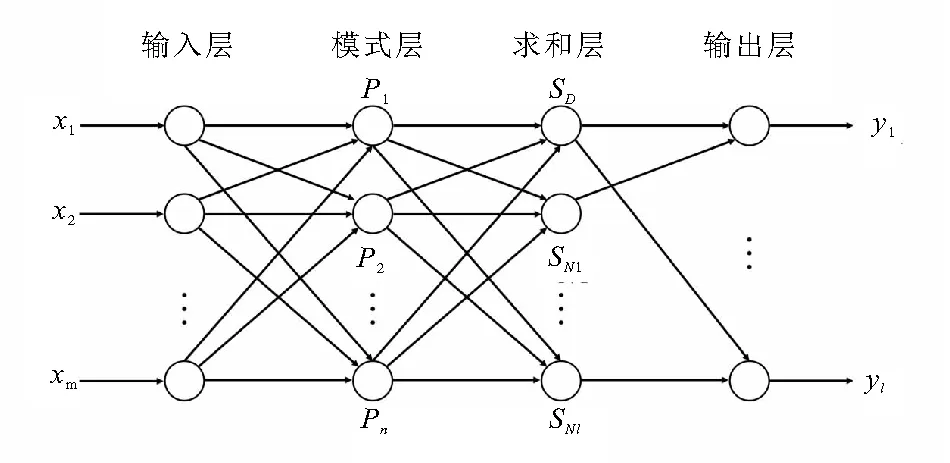
图2 广义回归神经网络结构[35]

平滑参数k对GRNN的预测性能影响较大，在训练样本确定后，网络的训练实际上是不断调整平滑参数以获得最佳回归估计结果的过程。为确定平滑参数，令平滑参数以增量Δk在范围[kmin,kmax]内递增变化，文献[35]给出了kmin的计算方法：

(6)

式中Dmin为训练样本中各输入向量之间Euclid距离的最小值；R为计算机能表达的最小正整数。

在训练样本中，依次取出一个样本，用剩余的样本构造GRNN对取出的样本进行估计，得到估计值与样本值之间的误差；对每一样本重复该过程，得到误差序列；将误差序列的均方值

(7)

作为网络性能的评价指标，将最小的误差序列均方值对应的平滑参数用于最后的GRNN。

2 基于GRNN的粘接界面内聚参数反演

2.1 总体思路

图3显示了双悬臂夹层梁I型断裂时加载点载荷-位移曲线的一般形式，不同加载位移wi(i=1,2,…,m)下加载点支反力F(wi)所组成的向量由内聚强度ft、断裂韧性GIc和位移系数d(初始刚度K)唯一确定，其中m表示离散的加载位移点数量，即存在函数g使

(8)

同样存在反函数g-1使

(9)

反函数g-1的具体形式由GRNN以数值形式给出。

图3 双悬臂夹层梁加载点载荷-位移曲线的一般形式

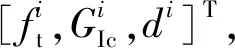
(10)

2.2 样本生成

采用文献[21]中双悬臂夹层梁的参数，在ABAQUS中建立了如图4所示的三维双悬臂夹层梁模型。双悬臂夹层梁有限元模型的具体参数如下：预制裂纹长度为30 mm，试件宽度为10 mm，长度为150 mm，加载块的长、宽、高分别为20、10、25 mm，加载孔半径为3 mm。铝合金基板厚5 mm，其弹性模量为70 GPa，泊松比为0.33，网格设为C3D8R单元；三元乙丙橡胶薄膜厚度为0.8 mm，其粘超弹本构参数如表1所示，网格设为C3D8H；粘接层厚度为0.5 mm，网格设为COH3D8，在垂直方向上只设置一层。铝板与三元乙丙橡胶薄膜、三元乙丙橡胶薄膜和粘接层之间采用绑定约束，下层铝板左下角固支，上层铝板左上角施加垂直向上的位移载荷U2=3 mm。

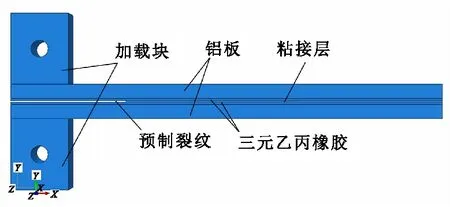
图4 三维双悬臂夹层梁模型[21]

表1 三元乙丙橡胶本构模型参数[21]

文献[26]通过修正梁理论(Correct Beam Theory，CBT)计算了图4中粘接层的内聚强度ft=0.548 MPa和断裂韧性GIc=0.087 6 kJ/m2。周清春等[31]已经证明位移系数在一定范围内改变仅对加载点载荷-位移曲线的上升段有影响，但位移系数过大会导致数值结果与实验结果不匹配。为确定通过FEA生成数据样本时位移系数的合理取值，将内聚强度和断裂韧性设置为文献[26]的结果，在0～100范围内改变位移系数d，计算得到加载点载荷-位移曲线如图5所示。图5中，位移系数为2时，载荷-位移曲线的上升段与实验结果偏差较大；位移系数为10、30、50、100时的载荷-位移曲线均与实验结果吻合较好。

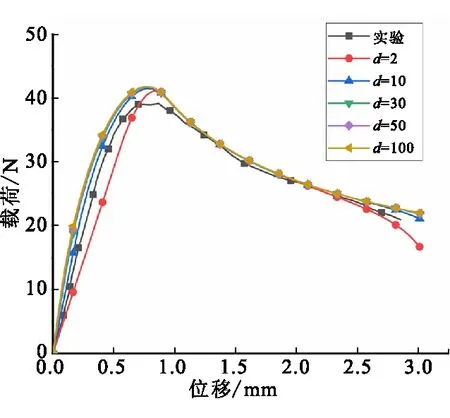
图5 不同位移系数下加载点的载荷-位移曲线

为获得建立GRNN所需的训练样本，首先将文献[26]中的采用CBT计算的内聚强度和断裂韧性均依次偏置-20%、-10%、0、10%、20%；根据图5的计算结果，将位移系数设置为26、28、30、32、34。采用正交实验设计的方法设计了3因素5水平的正交表，将正交表中的参数值带入有限元模型计算，得到25组加载点的载荷-位移数据。

计算得到的25组加载点载荷-位移数据的横坐标(位移)均不相同，不能将其直接作为训练样本。因此，采用分段线性插值方法对25组加载点载荷-位移数据进行处理，计算得到与位移向量[0.15,0.3,…,3]相对应的加载点载荷向量[F(w1)i,F(w2)i,…,F(wm)i](m=20;i=1,2,…,25)。

2.3 内聚参数反演

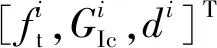
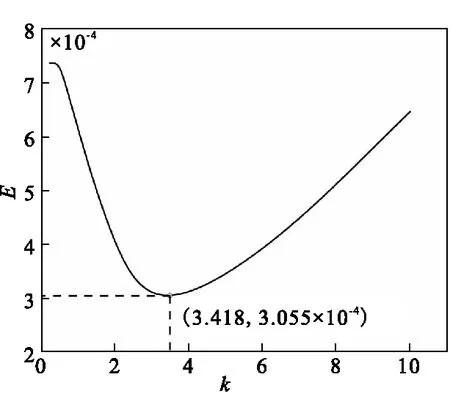
图6 平滑参数的确定

表2列出了采用文献[26]中的修正梁模型(CBT)、文献[25]中的Hooke-Jeeves算法(HJ)及其代码、本文所述基于GRNN的反演方法计算的粘接界面内聚参数。将表2中的3组内聚参数分别代入有限元模型进行计算(初始刚度均设置为32.687 N/mm3)，得到加载点的载荷-位移曲线与实验曲线的对比结果如图7所示。

表2 内聚强度和断裂韧性

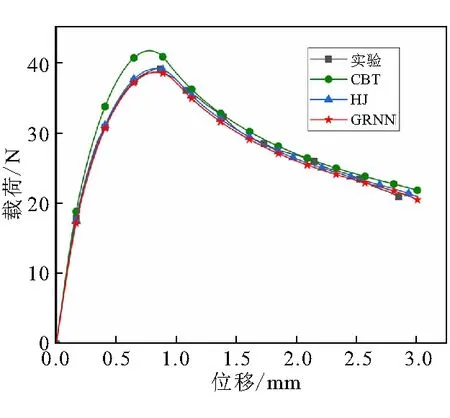
图7 加载点载荷-位移曲线对比

为计算表2中粘接界面的内聚参数，采用Hooke-Jeeves算法需要进行62次有限元分析，基于GRNN的反演方法则只需要进行25次有限元分析。说明与基于Hooke-Jeeves算法获取粘接界面内聚参数的反演方法相比，基于GRNN的反演方法能够更加快速地获取粘接界面的内聚参数。

图7中，与CBT方法对应的加载点载荷-位移曲线与实验曲线之间的最大相对误差为6.67%，与GRNN对应的加载点载荷-位移曲线与实验曲线之间的最大相对误差为1.12%。说明与采用CBT直接处理实验数据获取粘接界面内聚参数的方法相比，基于GRNN的反演方法能更加准确地获取粘接界面的内聚参数。

3 结论

(1)Hooke-Jeeves算法和广义回归神经网络分别需要进行62轮次和25轮次有限元分析以获取三元乙丙橡胶薄膜粘接界面的力学性能参数，与基于Hooke-Jeeves算法的反演方法相比，基于广义回归神经网络的反演方法能够更加快速地获取粘接界面的力学性能参数。

(2)基于修正梁模型和广义回归神经网络获得的加载点载荷-位移曲线与实验曲线之间的最大相对误差分别为6.67%和1.12%，与采用CBT直接处理实验数据获取粘接界面内聚参数的方法相比，基于广义回归神经网络的反演方法能够更加准确地获取粘接界面的力学性能参数。

(3)基于Hooke-Jeeves等优化算法对粘接界面力学性能参数进行反演时，调用的有限元计算轮次是不可预计的，反演过程是漫长甚至不收敛的。基于广义回归神经网络对粘接界面力学性能参数进行反演时，平滑参数是唯一需要预先指定的参数，调用的有限元计算轮次是可预计的(如本文通过正交实验设计的方法，确定了反演过程中只需进行25轮次的有限元计算)，这种将有限元结果作为广义回归神经网络训练样本的反演方法在求解大规模工程问题中的多参数反演问题时能节省大量的计算成本，具有一定的参考价值。