铺层结构对复合材料层合板固有频率的影响 *

牛雪娟，张 准，杨 涛,2

(1. 天津工业大学 机械工程学院，天津 300387；2. 天津市现代机电装备技术重点实验室，天津 300387)

0 引言

复合材料在现代生活中应用很广泛，它不仅具有较高的比强度和比刚度，且可减轻结构的质量、优化材料的某些物理和化学性质。复合材料层合板结构的多样性、参数可设计性、性价比较优等特点被广泛用于新型民用飞机、航天工程、高速列车等高科技领域[1-2]。但无论是在哪个领域，工况下都容易受到激励的作用引起整个结构的振动[3]。因此，对复合材料层合板的振动特性研究具有极其重要的实际意义。

黄凌志等[4]采用一种基于高阶剪切变形理论来获得任意形式铺设层合板的固有频率。师俊平等[5]基于哈密顿最小作用量原理，推导了复合材料层合板在任意铺层下的自由振动变分方程,并运用Ritz法对一般边界条件下多种铺层矩形板的基频进行了计算。杨杰等[6]考虑中面载荷的影响因素，对边界为混合型约束情况下的矩形层合薄板的振动特性进行了研究，得出了基于子域分解技术的单向DQ离散形式和半解析 Galerkin算法,并利用算例来分析混合边界组成、面内荷载和纤维铺层方式等的层合板振动特性的影响。Salawu[7]综述了基于固有频率变化的损伤识别文献。他表明了使用精确测量的模态频率数据在工程结构的损伤检测和状态监测是可行的。Oh等[8-9]基于分层理论研究了桶状复合材料层合板的动态响应和振动特性，得出全分层阻尼模型能准确地预测具有粘弹性层的圆柱形混合板的振动和阻尼。Abrate[10]利用Rayleigh-Rite法，对矩形层合板在任意线性支承状态下的固有频率进行研究，并给出了非空间层合板参数组成的多项式近似函数，得出最佳铺层结构是对称的角度层板。Berthelot等[11]对一端固支条件下的复合材料层合板进行动力响应测试。试件水平方向一端固支，采用力锤进行激振，激光测振仪进行拾振，将激励和响应信号转换为数字信号，由动态分析仪输入到电脑模态识别软件，获得所需频响函数、固有频率和模态振型。漆文凯等[12]采用逐点激励单点测试的方法，对自由状态和一端固支状态下的无损伤和含开孔损伤的复合材料层合板进行了模态试验和模态识别，得出层合板的开孔损伤位置和开孔的大小对层合板的振动特性有明显影响。

以上研究工作中，均没有对四角简支的复合材料层合板进行铺层角度与固有频率的模态振动测量与验证，大部分都是理论基础研究。本文将测量四角简支的复合材料层合板的固有频率和振型，并研究层合板的铺层顺序和固有频率的影响，借鉴结构振动频响分析的方法来研究复合材料层合板的振动特性。

1 模态振动实验

1.1 试件的制备

手工制作不同铺层结构的碳纤维层合板。首先将预浸料裁剪成尺寸为300 mm×300 mm×2 mm，通过树脂将单层板粘合在一起，在经过真空罐加热固化，形成铺层顺序为：[0°]16、[0°/90°]s8、[0°/90°/±45°]s4的层合板,最后经过水切割得到尺寸为：150 mm×100 mm×2 mm的层合板(试件)。

1.2 实验方案

实验中使用DH5927动态数据采集仪器，采样频率为12.8 kHz,层合板的单个测点实验采样选择瞬态线性平均采样方式，平均次数为4次，频域线数为400。复合材料层合板尺寸轻小，选择轻质的DH131E加速度传感器,灵敏度为1.04 mV/(m/s2)。力锤是复合材料专门做模态分析试验专用的LC02型号力锤，灵敏度为2.009 mV/N。

实验主要是为获得四角简支碳纤维复合材料层合板的前三的固有频率及振型。为确保加速度传感器与层合板能够紧密接触，选择强力粘胶粘结方式，加速度传感器只输出Z轴方向的加速度信号。

1.3 实验过程

为更好地测出层合板的模态振动特性，在层合板上选取9个点，各点的分布如图1(b)所示，其中5号点为锤击点，其余的8个点是层合板的测点。将压电式加速度传感器依次粘结在层合板的各个测点上。在锤击点5号点位处施加一个激励，通过DH5927动态信号测试分析系统获得频响函数曲线、力锤的力曲线、加速度曲线。最后将模态振动实验测得数据导入东华模态分析软件(DHMA软件)中，在分析中使用峰值搜索方法中的正交多项式来计算层合板单个测点的数据得到层合板的稳态图，从稳态图中可获得层合板的固有频率。模态振动实验如图1所示。

(a) 实验平台 (b) 层合板的各个点布局图

2 模态振动结果与讨论

进行模态振动实验前测得层合板的质量为(50±1) g，层合的质量误差较小，在结果讨论中忽略质量误差带给层合板固有频率的影响。实验中为更好地测得铺层角度对层合板固有频率的影响，采用三种不同铺顺序的碳纤维复合材料层合板，其中纯0°层合板有6块在本文中记为1系列，[0°/90°]s8层合板有5块在本文中记为2系列，[0°/90°/±45°]s4层合板有6块在本文中记为3系列。

2.1 1系列铺层角度对固有频率的影响

图2是纯0°复合材料层合板的瀑布图。由图2可清晰地看出在相同的激励点位置处激励，层合板的8个测点对应的各阶次的固有频率的误差均在10%以内，在实验误差范围内，可得测点的位置变化对层合板的固有频率的影响较小。但测点的位置不同会影响频响函数的幅值在2.6～9.6 mm之间浮动。随着阶次变大频率的幅值也逐渐增大，固有频率阶次与幅值之间呈非线性关系。

图3是纯0°层合板的频率误差柱状图。从图3可看出纯0°层合板的不同阶次的固有频率，将6块层合板的固有频率进行平均计算，得到层合板的一阶固有频率的平均值为647.9 Hz；二阶固有频率的平均值为1579.3 Hz；三阶固有频率的平均值为2875 Hz。其一阶固有频率误差最大的层合板是1-2，误差率为5.46%。二阶固有频率误差最大的层合板是1-5，误差率约为9.767%。三阶固有频率误差最大的层合板是1-4，其误差率约为5.217%。其中一阶和三阶固有频率相对稳定，二阶固有频率误差浮动较大，但小于10%是在误差允许范围内。1-5号层合板的二阶固有频率误差较大是由于激励1-5号层合板时二阶在模态上活跃层合板的质量比较大，使得1-5号层合板的二阶固有频率偏低 ，导致误差较大。

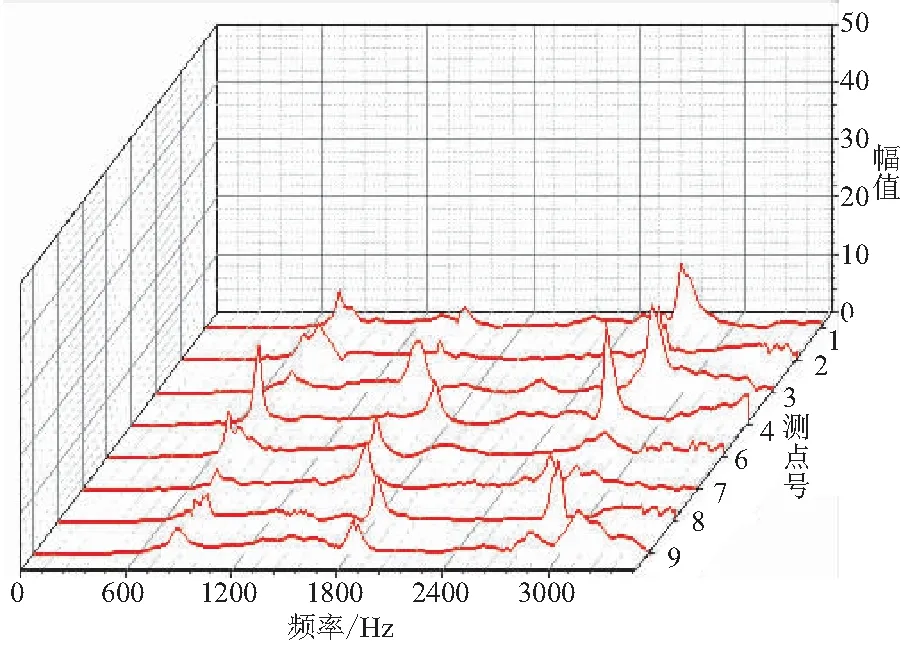
图2 纯0°层合板瀑布图

图3 纯0°层合板的频率误差柱状图

2.2 2系列铺层角度对固有频率的影响

图4是[0°/90°]s8层合板的瀑布图。可见，层合板上8个测点对应的频响函数。在激励点位置不变条件下，一阶固有频率在750 Hz左右变动，二阶固有频率在1850 Hz左右变动，三阶固有频率在2850 Hz左右变动。虽然测点位置不同，但所对应的固有频率影响是很小的。

从图4可清晰看出[0°/90°]s8层合板的一阶固有频率基本上没有随测点位置的变化而变化，但在二阶、三阶时[0°/90°]s8层合板的测点位置会引起频响函数的幅值在5.6～39.2 mm之间浮动。随着阶次变高幅值逐渐增大，固有频率的阶次与幅值呈非线性关系。可得测点的位置改变会影响幅值的大小。

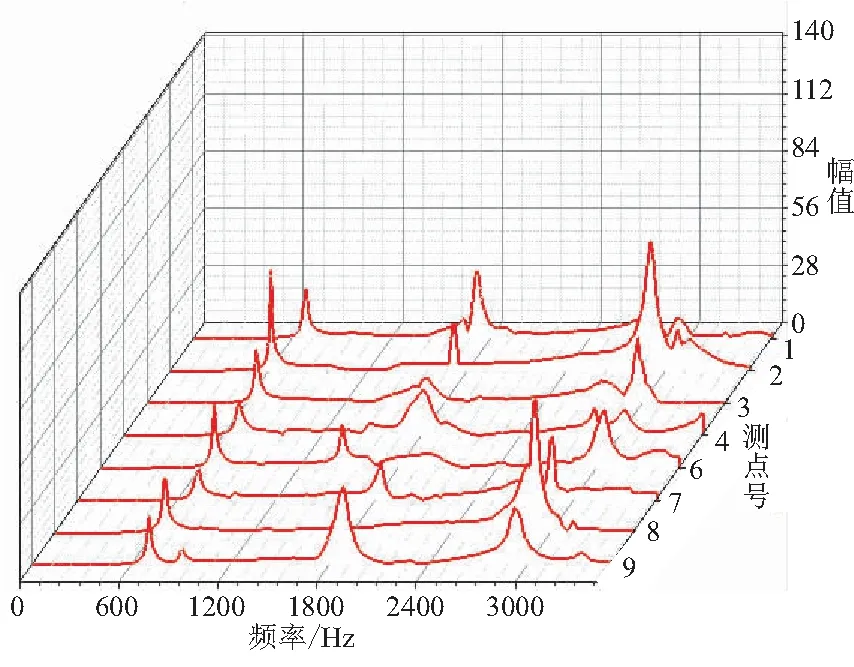
图4 [0°/90°]s8层合板瀑布图

图5是[0°/90°]s8的层合板的频率误差柱状图，可看出[0°/90°]s8铺层结构5块层合板的一阶固有频的平均值为747.5 Hz；二阶固有频率的平均值为1850 Hz；三阶固有频率的平均值为2887.5 Hz。其中一阶固有频率误差最大的层合板为2-1，其误差率为7.023%，二阶固有频率误差最大的层合板为2-1，其误差率为3.378%，三阶固有频率误差最大的层合板为2-2，其误差率为3.463%。2-1号层合板一阶、二阶固有频率不稳定，尤其二阶存在频率误差比较大，这有可能是由于2-1号层合板在制造过程中树脂流动不均匀造成的。

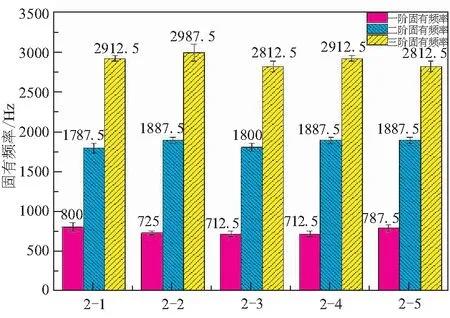
图5 [0°/90°]s8纯层合板的误差柱状图

2.3 3系列铺层角度对固有频率的影响

由图6[0°/90°/±45°]s4层合板的瀑布图可看出层合板的8个测点对应的频响函数。在激励点位置不变条件下，测点位置的改变对层合板的固有频率有很小的影响。然而，层合板的测点位置变化会引起频响函数的幅值在3.6～15.4 mm之间浮动。随着固有频率的阶次变高幅值逐渐增大，阶次与幅值呈非线性关系。由此可得测点位置的改变对层合板的幅值的大小影响较大，而对固有频率的影响较小。

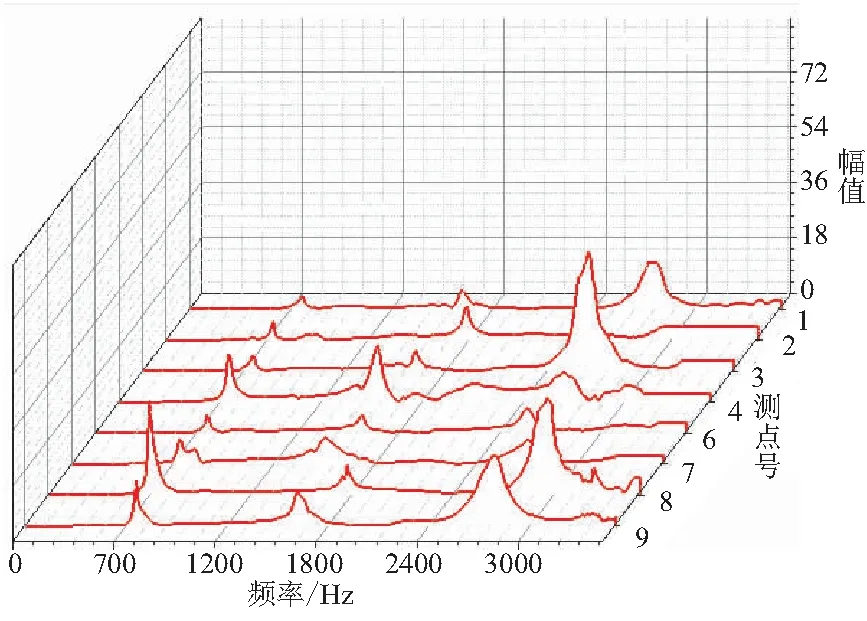
图6 [0°/90°/±45°]s4层合板瀑布图

图7为[0°/90°/±45°]s4的层合板的频率误差柱状图，可得到[0°/90°/±45°]s4铺层顺序的6块层合板的一阶固率的平均值为733.3 Hz；二阶固有频率的平均值为1808.3 Hz；三阶固有频率的平均值为2933.3 Hz。一阶固有频率误差最大的层合板为3-5，其误差率为7.391%。二阶固有频率误差最大的层合板为3-1，其误差率为10.138%。三阶固有频率误差最大的层合板为3-1，其误差率为7.102%。3-1号层合板无论是二阶还是三阶的固有频率都不稳定，可能是由于3-1号层合板在加热固化时受到温度、压力等因素影响，使树脂和纤维流动不均，造成层合板形成较多的气泡。导致3-1层合板固有频率误差，振动特性不稳定。

图7 [0°/90°/±45°]s4纯层合板的误差柱状图

3 不同铺层结构对固有频率的影响

3.1 前三阶固有频率变化图

层合板的一阶固有频率(简称为基频)的大小是衡量结构振动特性的关键指标，基频是越高越好，基频越高层合板的结构整体刚度越高、稳定性越好、抗冲击能力越强，可降低层合板共振的发生率。

为更好地研究不同铺层结构对层合板的固有频率的影响，对不同铺层的同一阶频率进行对比，对比结果如图8所示。

(a)一阶频率变化曲线图 (b)二阶频率变化曲线图 (c)三阶频率变化曲线

由图8(a)一阶频率变化曲线图，可明显地看出纯0°铺层角度的层合板的一阶固有频率远低于2系列、3系列的层合板的一阶固有频率，其中3系列[0°/90°/±45°]s4铺层顺序的层合板的一阶固有频率总体趋势超过2系列[0°/90°]s8铺层顺序的层合板的一阶固有频率。从图8(b)、图8(c)可分别看出，无论是在二阶、三阶固有频率时，[0°/90°/±45°]s4铺层顺序的层合板固有频率均高于其他两种固有频率。这是由于45°纤维铺层的存在使3系列的层合板的抗冲击能力及稳定性等性能得到了提升，进而使其不易发生共振现象。

3.2 不同铺层结构对振型的影响

为研究不同铺层结构对振型的影响，测得不同铺层结构的模态振型图，如图9～图11所示。由图9、图10及图11可看出来一阶模态振型为层合板的长边与短边都凸起，振型呈V形；图11(b)二阶模态振型为层合板的短边凸起，图9(b)、图10(b)二阶模态振型还伴有扭动，振型呈S形；图10(c)、图11(c)三阶模态振型为层合板的长边凸起，且图9(c)三阶模态还伴有扭动，振型整体呈W形。从图11可清楚看出层合板的振型，无论处于哪种状态其变形量都是相对较小，不易发生共振。说明[0°/90°/±45°]s4层顺序层合板的振动特性比较优越。

(a)一阶模态振型图 (b)二阶模态振型图 (c)三阶模态振型图

(a)一阶模态振型图 (b)二阶模态振型图 (c)三阶模态振型图

(a)一阶模态振型图 (b)二阶模态振型图 (c)三阶模态振型图

4 结论

(1)从振动模态实验测试结果可看出固有频率为全局变量。层合板的铺层结构决定固有频率的大小，而测点位置的变化对固有频率的影响是很小的。测点位置的变化会引起频响函数的幅值变化，幅值随固有频率阶次的变高呈非线性变化。

(2)四角简支的纯0°铺层结构的复合材料层合板的一阶固有频率的平均值为647.9 Hz；二阶固有频率的平均值为1579.3 Hz；三阶固有频率的平均值为2875 Hz。[0°/90°]s8层合板的一阶固有频率的平均值为733.3 Hz；二阶固有频率的平均值为1808.3 Hz；三阶固有频率的平均值为2933.3 Hz。[0°/90°/±45°]s4层合板的一阶固有频率的平均值为747.5 Hz；二阶固有频率的平均值为1850 Hz；三阶固有频率的平均值为2887.5 Hz。

(3)通过分析不同铺层角度的复合材料层合板的固有频率及振型，得出纯0°铺层顺序的复合材料层合板的基频远低于另外两种的基频，最容易发生共振。[0°/90°/±45°]s4复合材料层合板能有效降低共振发生率，有利于提高结构整体的刚度及振动性能。