电磁场耦合忆阻神经网络的放电模式及同步行为研究

谭安杰，韦笃取，覃英华

(广西师范大学 电子工程学院，广西 桂林 541004)

生物神经元是大脑处理信息的基本单元。每个神经元通过突触相连，组成复杂的神经网络，并呈现出复杂的非线性动力学行为[1]。神经元作为产生感觉、学习、记忆和思维等认知功能器官的基本单元，其动力学行为与脑功能密切相关。大脑对神经信号的辨析是通过不同脑部的大量神经元共同实现，因此同步作为神经元集群放电的典型表现形式，是神经信号处理的重要机制。当前，神经网络的放电模式及同步行为分析是国内外的研究热点[2-7]。如周小荣等[8]研究小世界网络的节点数和近邻数对网络同步的影响；Shi等[9]和Xu等[10]发现提高突触耦合强度可以增强网络同步程度；Shafiei等[11]研究了部分时延对网络同步的影响；Jin等[12]发现强噪声使神经元调节功能失去同步，甚至损害神经元本身功能。

另外，大量的实验[13-15]表明，当动物长时间暴露于电磁脉冲时，电磁辐射会影响其神经元的电活动，甚至会诱发认知损伤。而在时变磁场环境下，神经元会产生感应电场，在膜电位连续波动时，电场分布对神经元的影响变得更明显。因此，在传统的神经元模型中引入磁场和电场变量对细胞的生理活动规律及其物理机制研究具有实际意义。如：Lv等[16]发现磁通量可用于描述电磁辐射对神经元膜电位的影响；Ma等[17]发现膜电位在加入电磁辐射中产生心力衰竭的异常现象；Xu等[18]研究膜电位在电磁感应效应下放电模式转换，还讨论了膜电位之间的生物联系；Ge等[19]发现周期高频电磁感应对HR神经网络模型的电活动有不同的影响。另一方面，忆阻器是蔡少棠教授1971年根据经典电磁场理论预测出来的一种新电子器件。2008年美国惠普实验室在研究二氧化钛的时候发现并证实了纳米电子忆阻器的存在。忆阻器的纳米尺寸、信息存储能力和掉电后信息的非易失性，不但广泛应用在各个领域[20]，而且非常适合作为神经元的耦合突触[21-22]。

鉴于上述研究背景，本文首先提出一种考虑电场和磁场的神经网络模型，使用磁控忆阻器模拟细胞内的磁感应效应，描述磁通量和膜电位之间耦合；然后通过数值仿真研究电磁感应对神经网络的放电模式转换以及网络同步行为的影响；最后，实验表明，膜表面电荷尺寸与磁控忆阻反馈增益能改变神经网络放电模式，而增加突触耦合强度能改变网络同步性能。与以往研究离子电流活动对单个神经元影响的工作相比，本文研究的新模型采用突触耦合形式实现网络节点间的连接，并且考虑电荷分布引起的电场效应以及磁通量引起的磁场效应，因而更具实际意义。

1 模型和方法

以Hindmarsh-Rose(HR)神经元为节点，建立具有电磁场突触的全耦合忆阻神经网络模型[23-24]：

(1)

其中：x、y、z分别表示膜电位、快速电流恢复变量和自适应电流项；参数Iext表示注入外界刺激电流；本文选取参数a=1.0，b=3.0，c=1.0，d=5.0；下标i描述网络中的节点序号；g0是突触耦合的耦合强度；变量φ表示穿过膜的磁通量；k1x和k2φ描述膜电位诱导的磁感应变化和磁通泄露；磁通量k1=0.9；膜电位互相作用k2=0.5。式子kρ(φ)x认为是电磁感应对膜电位的反馈电流，其方程为：

(2)

其中：膜电位磁控忆导为ρ(φ)；选择参数反馈增益k=1；无量纲参数α、β分别取0.1、0.02。

由于神经元含有大量带电离子，如钾钠离子在细胞内流动，造成膜电位发生变化，膜认为是具有一定均匀电荷分布的带电表面。因此，神经元暴露于外部电场时，神经元固有电场被调制，动力学方程为[25]：

(3)

其中函数f(·)定义为膜电位，g(·)定义为跨膜电流。式(3)中新添电场变量E可用于描述离子在细胞内交换引起的离子分布和膜电位的敏感性，变量y添加rE源于快速电流对极化和感应电场的敏感。r是当电荷被视为球形时的半径尺寸，k3是极化特性参数，Eext表示外部电场。一般采用高斯白噪声辐射ξ(t)[26]对膜电位调节不同模式的电活动，其统计特性为：

(4)

其中D0是噪声强度，δ(·)是狄拉克函数。

为了判断神经网络的同步程度，根据平均场理论得到同步参数的计算公式：

(5)

其中N为神经元数，〈·〉为随时间变化的平均值，T为瞬态周期，以T=20 000进行数值仿真。当R趋于1时，接近完全同步，而R接近0时，非完全同步。

2 数值结果与讨论

在本节的数值仿真中，使用四阶Runge-Kutta算法，时间步长h= 0.01，选择50个同类型神经元，选择不同的初始值xi=0.02+0.1×i，yi=0.02，zi=0.5，φi=0.1+0.1×i，Ei=0.1+0.1×i，其中i为全局耦合网络的节点序号。计算60 000个时间单位，刺激电流Iext=2.3，固定极化特性参数k3=15，噪声强度D0=500。首先，计算单个神经元模型的峰-峰间隔(inter-spike interval，ISI)分岔图，以此分析忆阻反馈增益对系统稳定性的影响，结果如图1。由图1可知，反馈增益k在[0.4,0.5]内，神经元处于稳定放电状态。

然后取不同膜表面电荷尺寸r和磁控忆阻反馈增益k，观察神经元膜电位(节点i=30)的时间序列，结果分别如图2和图3所示。由图2可知，施加超过亚阈值刺激能激发神经元振荡，但随着电荷尺寸增加，神经元电活动受到抑制，由簇放电转换到静息态，体现电场效应中电荷尺寸对神经元电活动的调制。潜在机制是电荷尺寸和离子在膜上的连续流动可以建立膜上电场的时变分布，且外部电场可以改变自身电场的电荷分布，从而调制了离子的传输，影响了神经元电活动。反馈增益k描述了电磁感应通过忆阻器产生感应电流对膜电位的影响，为了研究感应电流对电活动模式选择的影响，本文调节反馈增益k观察电活动响应，结果如图3。由图3可见，随着磁控忆阻反馈增益k的增加，神经元电活动幅度减小，并从簇放电转换到尖峰放电状态，此现象表明了电磁对神经网络放电模式同样具有重大影响。

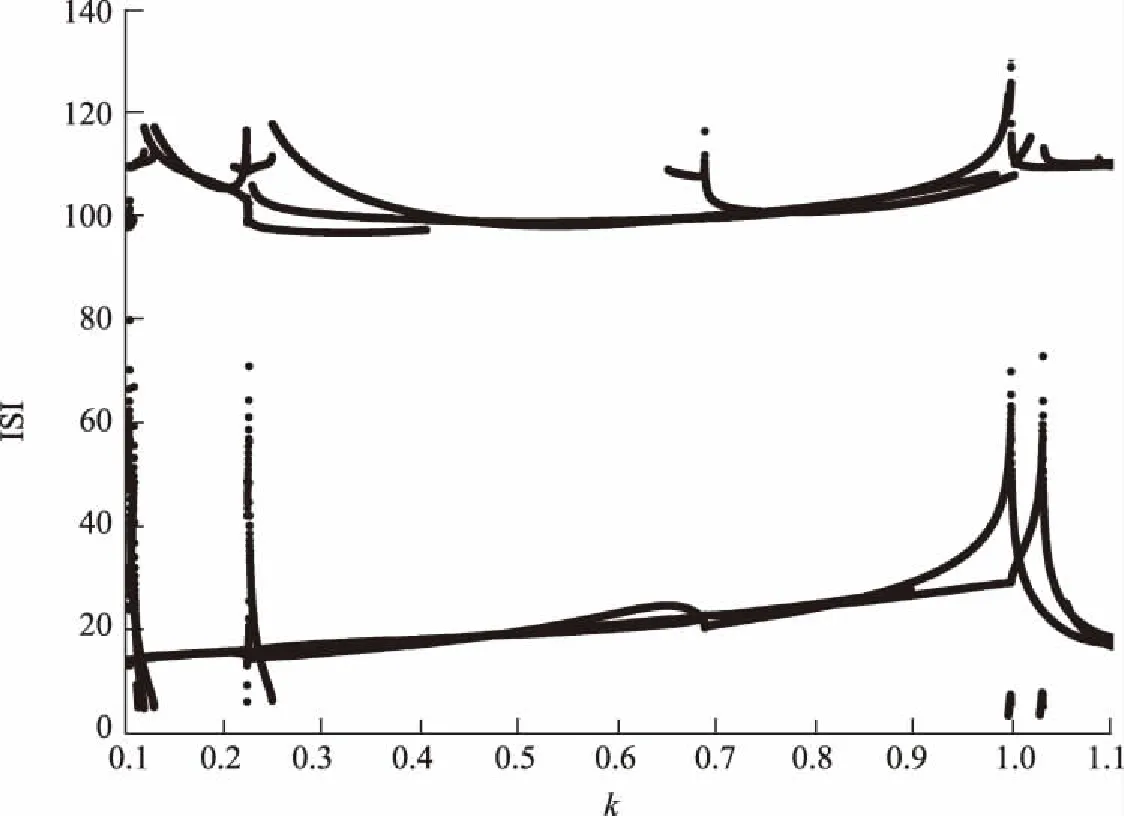
图1 ISI随反馈增益k变化的分岔图Fig.1 Bifurcation diagram of ISI versus feedback gain k

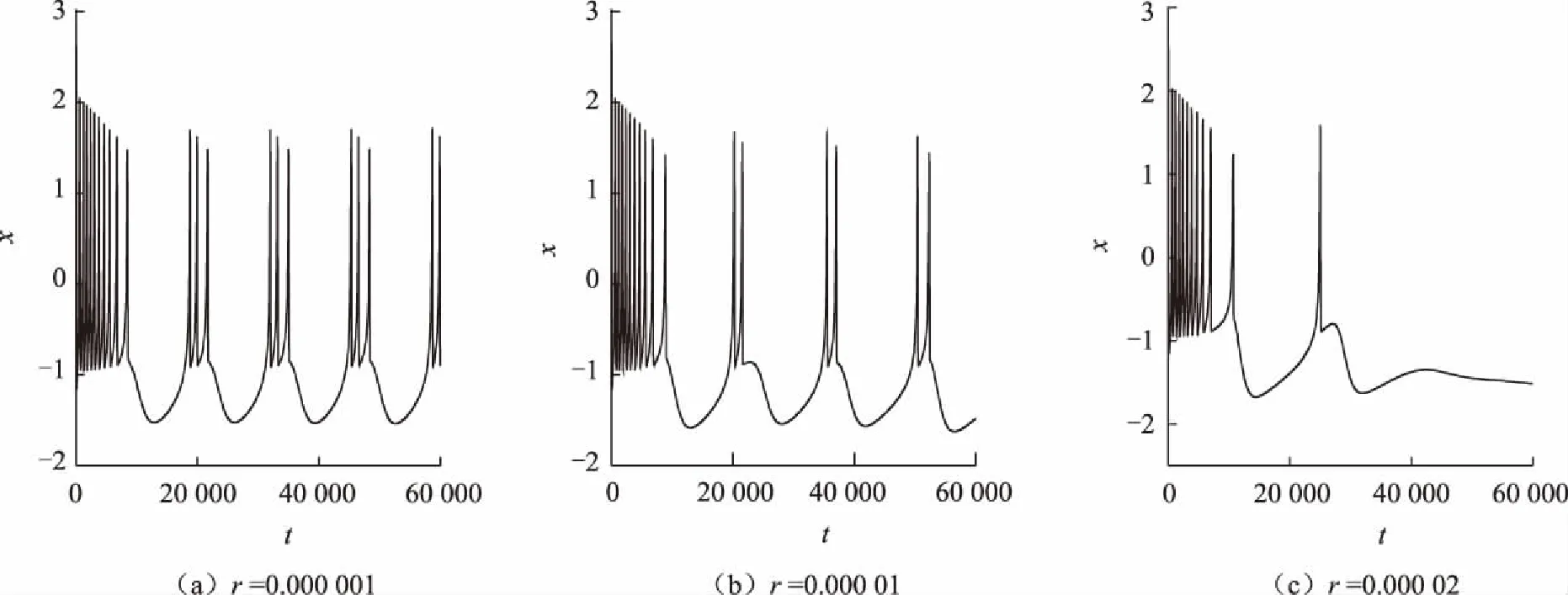
图2 考虑不同电荷尺寸r时，神经网络任意节点(i=30)的膜电位时序图Fig.2 Membrane potential of the arbitrary node in the neural network (i=30) with different parameter sizes r

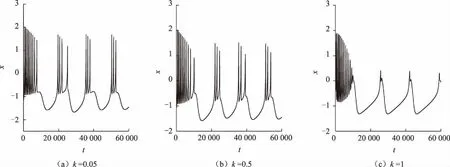
图3 考虑不同磁控忆阻反馈增益k时，神经网络节点(i=30)的膜电位时序图Fig.3 Membrane potential of the arbitrary node in the neural network (i=30) with different feedback gains k

参数取值r=0.000 001, D0=500，k=0.001。图4 突触耦合强度对同步参数的影响Fig.4 Synchronization parameters depend on synaptic coupling

接着研究突触耦合强度、磁控忆阻反馈增益和电荷尺寸对于神经网络同步的影响，其结果分别如图4～6所示。由图4可以发现随着突触耦合强度增大，同步参数逐渐变大，表明突触耦合在神经网络中有助于同步程度的演化，其潜在机制是神经元之间的信号传播和能量交换极大地依赖于突触连接的强度[27]。对比图5和图6，发现增大反馈增益和电荷尺寸几乎不能改变神经网络的同步性。这表明了忆阻反馈增益和电荷尺寸只能调节神经网络放电模式，不能改变神经网络的同步性。

参数取值r=0.000 001, D0=500，g0=0.001。图5 磁控忆阻反馈增益对同步参数的影响Fig.5 Synchronization parameters depend on the feedback gain

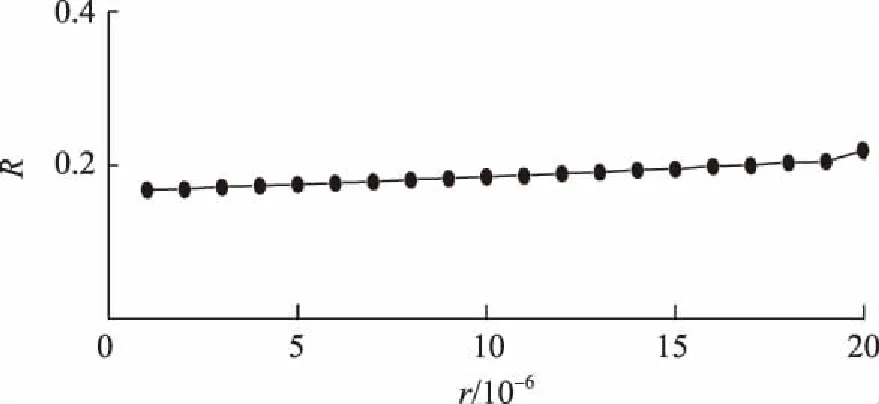
参数取值k=0. 1, D0=500，g0=0.001。图6 电荷尺寸对同步参数的影响Fig.6 Synchronization parameter depends on the charge size

3 结论

本文在研究具有磁控忆阻和电场效应的全局耦合HR神经网络的放电模式和同步行为，依据法拉第电磁感应定律，引入磁通变量，用忆阻器反馈调节膜电位。同时在通过引入新的场变量描述膜电位持续波动时，细胞膜表面的电场分布。研究发现，神经网络在固定的外部刺激下，增大电荷尺寸能抑制神经元电活动的兴奋性。此外，增大磁控忆阻反馈增益，即增大反馈电流也能改变神经元的放电活动。值得注意的是，电场感应与磁控忆阻反馈增益的调制均不能影响神经网络的同步性，只有增加突触耦合强度才可以显著提高神经网络的同步性能。研究结果可以为理解神经系统的信号编码和传播提供新的见解。