电网随机扰动下的光伏微网逆变器建模及控制研究
项琴琴,廖志贤,李廷会,蒋品群,黄国现
(广西师范大学 电子工程学院,广西 桂林 541004)
随着地球上不可再生能源的枯竭、环境问题不断凸显以及信息技术、工业技术的不断发展,“互联网+”智慧能源的环境应用应运而生。人类对可再生能源的利用技术越来越重视,尤其对利用太阳能、风能等可再生能源发电的研究愈加关注,而这些新能源发电技术的关键技术之一就是逆变器的设计[1],因此,建立正确的光伏微网逆变器的数学模型以及研究性能优良的控制方法显得尤为重要[2-3]。
光伏微网逆变器因其高效率、高灵活性和易于组网的特点[4],受到越来越多研究者的关注。传统的逆变器控制方法通常利用线性控制的理论与方法进行控制,但是采用线性控制器的逆变器,易造成输出电流波形失真,且动态特性差[5]。由于非线性模型预测控制可以处理系统的非线性,并且动态性能良好,近年来已经在电力电子行业得到了广泛的应用。逆变器比较常用的预测控制有模型预测控制、无差拍控制等[6]。文献[7]采用两步预测且同时分析最优开关函数组合及次优开关函数组合,一定程度上能克服电流振荡,但计算量大;文献[8]在预测电流控制方法的基础上提出了一种滤波电感在线估计方法,解决了电感误差引起的问题,但其未考虑系统延时影响,造成了输出电流与目标电流之间的偏差。由此可见,针对逆变器的控制策略仍具有优化空间。
为了进一步抑制谐波以及保持系统稳定,本文首先根据单相光伏微网逆变器的电路结构建立电压回路方程,接着由该方程微分形式推算出系统的输出控制表达式,并利用具有快速度与高精度的四阶龙格-库塔法进行模型迭代,引入积分补偿的预测控制对逆变器系统模型进行离散化分析,消除静态误差,有效控制输出电压和电流的稳定[9]。
1 单相光伏微网逆变器建模过程
光伏微网逆变器中,微网信号相当于系统的有源负载,电路中还应串联一个小的等效电阻与耦合电感,微网信号上施加随机扰动的单相光伏微网逆变器系统运行电路可简化为如图1所示。
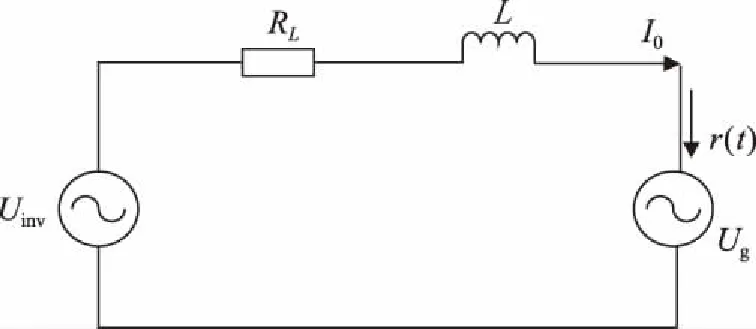
图1 单相光伏微网逆变器简化电路Fig.1 Single-phase photovoltaic microgrid inverter simplified circuit
图1中Uinv为单相光伏逆变器的输出电压,Ug为微网电压,r(t)是施加在微网信号上的随机扰动,Io为光伏微网逆变器注入微网的电流。根据回路电压法,可建立光伏微网逆变器的方程如下:
(1)
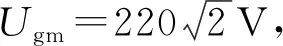
微分方程形式如下:
(2)
单相光伏微网逆变器注入微网的电流Io对微网电压Ug进行跟踪,因此输出电流Io是与微网电压Ug相位、频率同步的信号。由于随机扰动r(t)对微网信号的影响,使得微网逆变器输出的电压、电流波形出现失真,因此需要选择正确的控制方法保证系统输出的稳定[10]。
2 引入积分补偿的预测控制
2.1 预测控制方法
预测控制近几年在工业领域发展较快,采用多步测试、滚动优化[11]、反馈校正等控制策略[12],具有动态性能好、鲁棒性高等优点[13]。较为流行的预测控制算法包括动态矩阵控制(DMC)、模型算法控制(MAC)、广义预测控制(GPC)等。这些算法虽然在一些细节上有所区别,但是主要思想都是相似的。最基本的线性无约束预测控制算法与线性二次型控制很相似,具有解析解。在考虑约束时,一般在每个采样时刻进行实时求解。预测控制能充分利用计算机的强大运算功能,从而达到其优良的控制效果[14]。预测控制方法主要用于对系统进行离散化分析,预测系统未来的输出状态[15]。本文为方便对输出电流Io(t)进行预测,需要对式(1)进行离散化分析[10],使得Io(i+1)=Iref(i+1)。
离散化后方程形式如下:
(3)
由于RL接近于0,所以式(3)可写成:
(4)
现对Uinv(i)进行预测,假设微网电压Ug(i)是线性系统,则可推算出以下式子:
Ug(i)=Ug(i-1)+[Ug(i-1)-Ug(i-2)];
(5)
Ug(i+1)=Ug(i)+[Ug(i)-Ug(i-1)];
(6)
(7)
由式(5)~(7)可得:
(8)
由式(6)、(7)可得:
(9)
对式(8)、(9)得到的预测值求平均可得:
(10)
将式(10)结果代入式(4)可得:
(11)
由式(11)计算逆变器输出电压,使输出电流与期望电流相等[16],即Io(i+1)=Iref(i+1)。
2.2 引入积分补偿的预测控制
光伏微网逆变器传统预测电流控制算法由于采样与计算延时会造成差一拍控制,使得逆变器输出电流不能很好地跟踪目标电流,同时逆变器滤波电感模型值与实际值有误差时会造成输出电流谐波大,还可能导致系统不稳定[17]。针对本文微网信号上施加的随机扰动。引入积分补偿的预测控制既可以预测输出,跟踪目标电流,还能消除静态误差,有效抑制随机扰动。积分补偿是一种线性控制,将积分补偿环节通过线性组合构成控制量,对被控对象进行控制[18]。本文的微网逆变器系统使用引入积分补偿的预测控制方法使逆变器系统的电压输出Uinv(t)、电流输出Io(t)波形保持稳定。
令
e(i)=Io(i+1)-Io(i-1),
(12)
则积分补偿环节:
Ie(i)=Ie(i-1)+e(i)T。
(13)
将式(13)代入式(11)中,控制项表达式可表示为:
(14)
引入积分补偿主要用于消除静差,提高系统的无差度[19]。正确调整积分补偿环节的系数β,即可实现输出波形的稳定。其中系统开关周期T=0.02 ms,积分步长h=0.01 μs。
3 仿真结果与分析
本文利用基于MATLAB的Simulink平台搭建逆变器系统的仿真模型[20],并设置仿真时长为0.1 s,经过多次试验调试,对积分补偿环节的系数β作出调整,可确定当β=-46时,输出波形效果最为理想,如图2和图3所示。
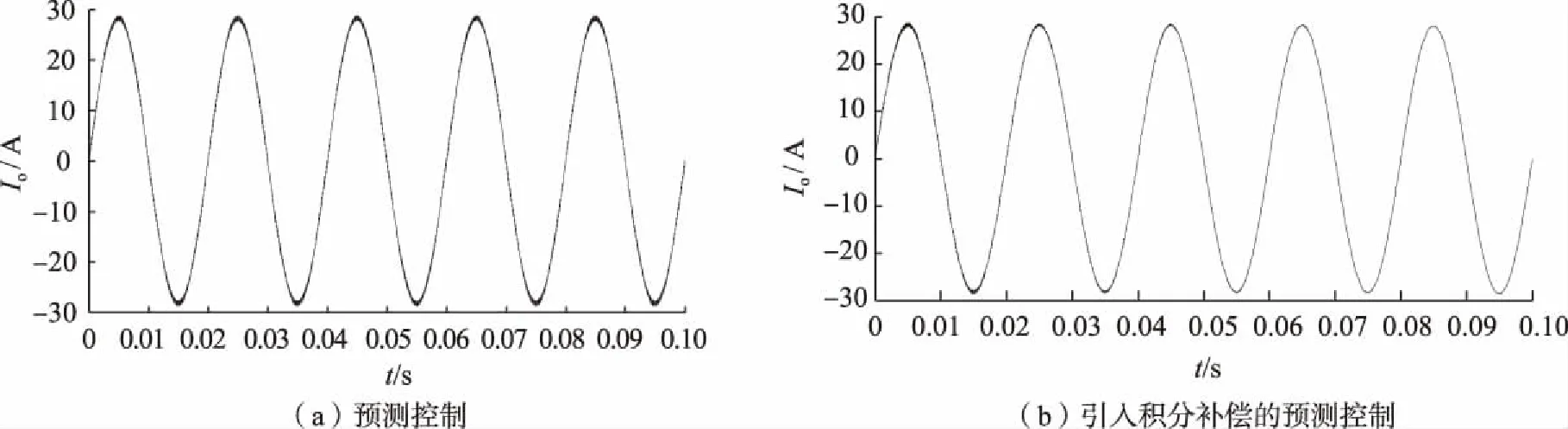
图2 预测控制、引入积分补偿的预测控制微网逆变器输出电流波形对比Fig.2 Predictive control, predictive control with introduction of integral compensation,comparison of output current waveform of microgrid inverter
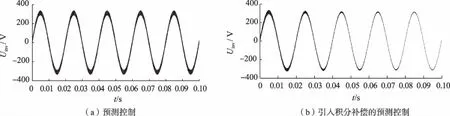
图3 预测控制、引入积分补偿的预测控制微网逆变器输出电压波形对比Fig.3 Predictive control, predictive control with introduction of integral compensation,comparison of output voltage waveform of microgrid inverter
由图2和图3对预测控制、引入积分补偿的预测控制的微网逆变器的输出电流、输出电压波形进行对比,可观察到输出电流与输出电压波形的振荡得到了很好的控制,说明引入积分补偿的预测控制方法使系统快速进入低谐波失真度状态,输出波形稳定性和质量都更好。
对时域上0.043~0.047 s时间段的输出电流波形进行放大,如图4所示。由图4可见,系统在预测控制下输出电流的绝对误差大约为1.2 A,误差较大;而引入积分补偿的预测控制下,输出电流的绝对误差大约为0.3 A,波形振荡明显减弱,说明引入积分补偿的预测控制对输出电流波形振荡抑制的有效性。
对时域上0.042 5~0.047 5 s时间段的输出电压波形进行放大,如图5所示。由图5可知,系统在预测控制下输出电压的波纹振幅大约为50 V,波动较大;而在引入积分补偿的预测控制下,输出电压的绝对误差大约为15 V,误差明显减弱,同时说明引入积分补偿的预测控制有效抑制了输出电压波形的振荡。可见引入积分补偿的预测控制对抑制逆变器系统的随机扰动具有一定效果,尤其注意积分补偿环节的系数要选择合适,过大或过小,都会使输出波形不理想。
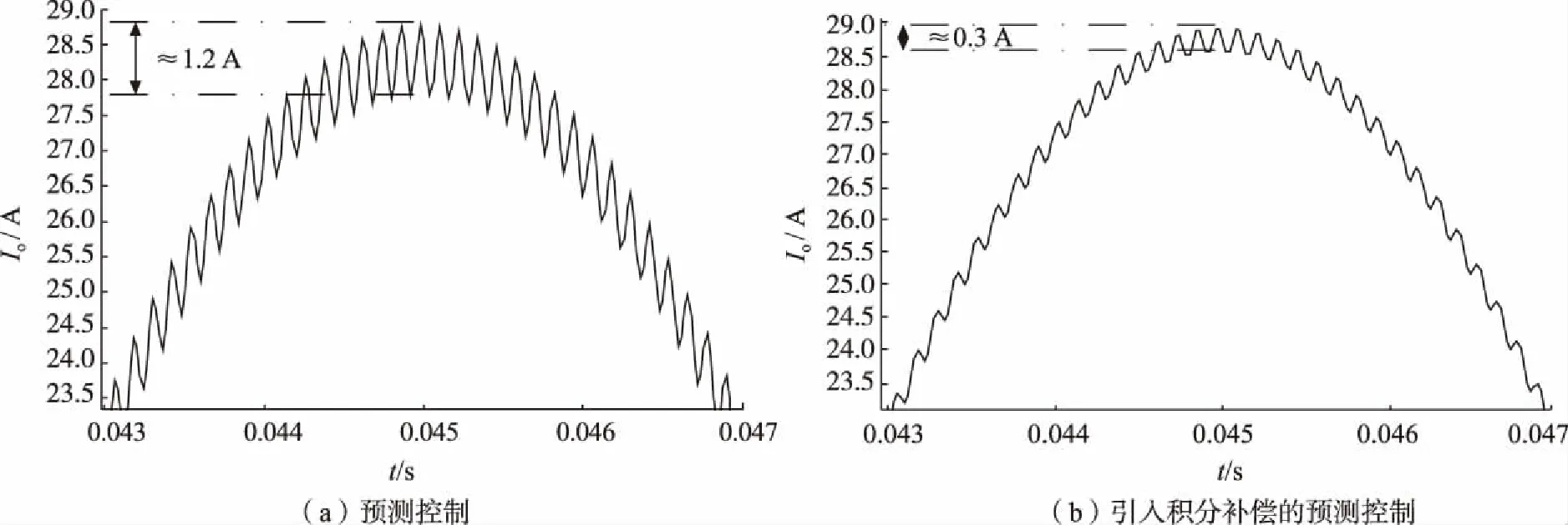
图4 预测控制、引入积分补偿的预测控制微网逆变器输出电流波形局部放大对比Fig.4 Predictive control, predictive control with introduction of integral compensation, comparison of partial amplified waveform of output current of microgrid inverter
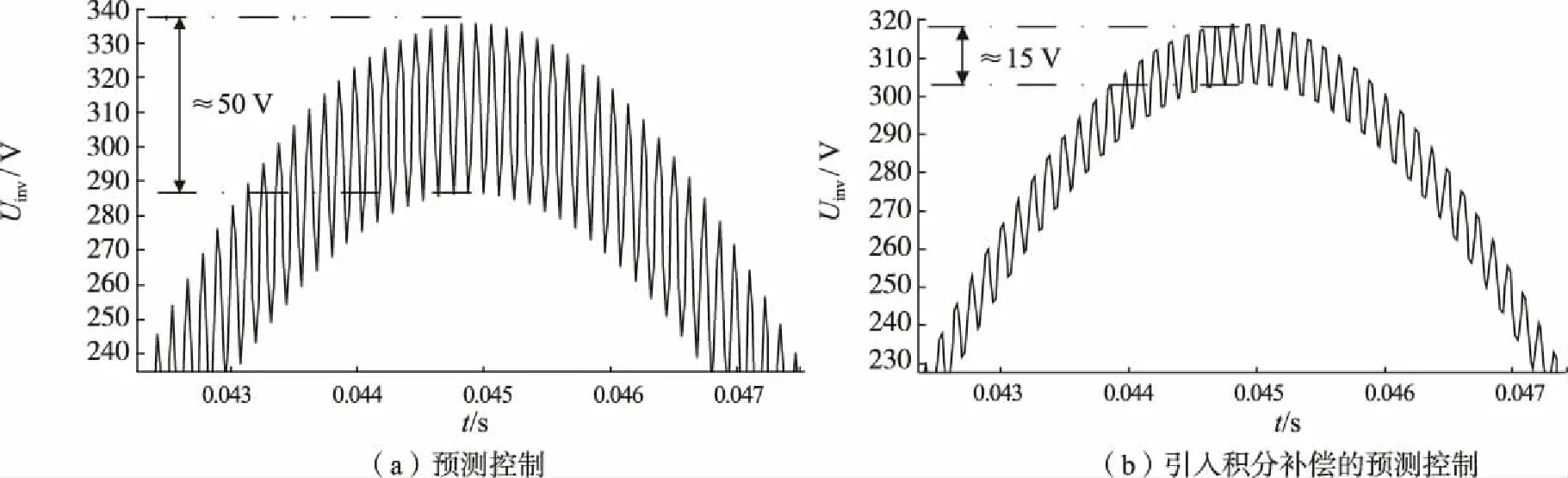
图5 预测控制、引入积分补偿的预测控制微网逆变器输出电压波形局部放大对比Fig.5 Predictive control, predictive control with introduction of integral compensation, comparison of partial amplified waveform of output voltage of microgrid inverter
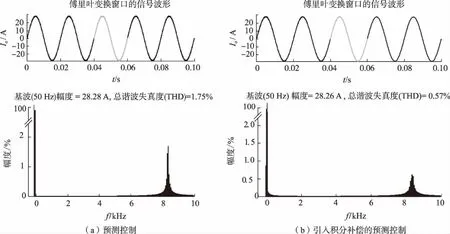
图 6 预测控制、引入积分补偿的预测控制微网逆变器输出电流总谐波失真度对比Fig.6 Predictive control, predictive control with introduction of integral compensation, comparison of total harmonic distortion of output current of microgrid inverter
对预测控制、引入积分补偿的预测控制的微网逆变器输出电流与输出电压进行快速傅里叶变换分析结果如图6和图7所示。从图6和图7可见,输出电流与电压的总谐波失真度(THD)分别由预测控制时的1.75%、7.94%降低为引入积分补偿的预测控制时的0.57%、2.57%。与未加入积分补偿的预测控制算法进行对比[21],结果如表1所示。由表1可知,加入积分补偿算法,可有效消除误差,抑制扰动,减小谐波振荡,保持系统稳定,说明本文改进的控制方法是可行和有效的。

表1 指标对比
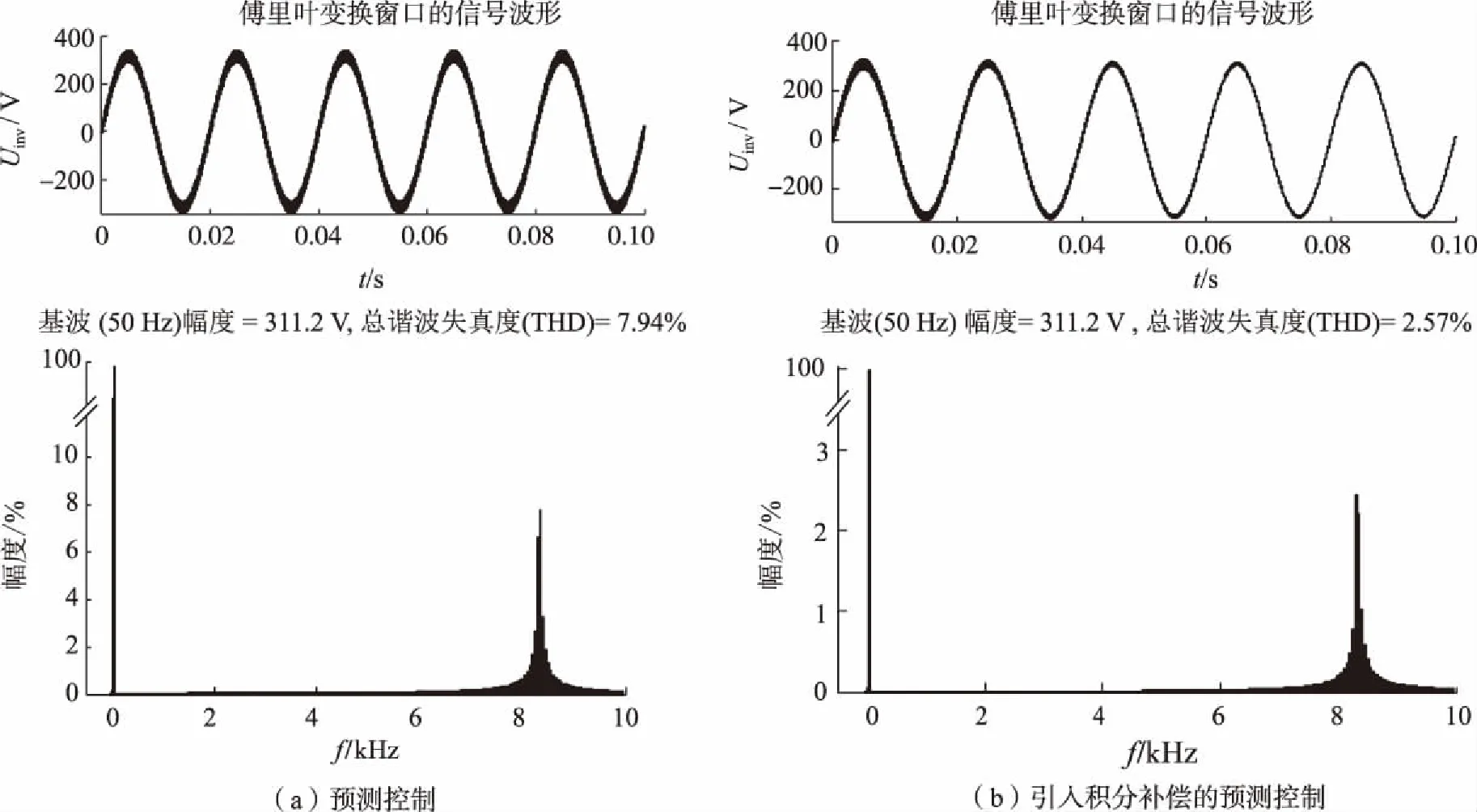
图 7 预测控制、引入积分补偿的预测控制微网逆变器输出电压总谐波失真度对比Fig.7 Predictive control, predictive control with introduction of integral compensation, comparison of total harmonic distortion of output voltage of microgrid inverter
4 结论
为了使研究更具现实意义(考虑到实际应用中微网电压并不是理想的正弦信号),本文主要研究在微网信号施加随机扰动的情况下单相光伏微网逆变器系统的建模,并利用引入积分控制的预测控制方法对下一周期的微网电压及输出电流进行跟踪预测,从而预测下一周期输出状态,可以有效抑制谐波,使得微网逆变器系统的输出电压、输出电流仍能保持较稳定的正弦波形。仿真结果表明这种改进后的控制方法具有明显的抗干扰能力,可有效消除误差,减小谐波振荡,保持系统稳定,对未来微网逆变器系统研究和开发具有一定的指导意义。

