一种自励式磁控电抗器的仿真分析
李晓明
(山东大学 电气工程学院,山东济南250061)
一种自励式磁控电抗器的仿真分析
李晓明
(山东大学 电气工程学院,山东济南250061)
磁控电抗器在电力系统有广阔的应用。现有的可用于超高压电力系统的自励式磁控电抗器的暂态相应时间很长,不能满足电力系统要求。提出一种可用于超高压电力系统的新型自励式磁控电抗器,并用Matlab/ Simulink构建自励式磁控电抗器仿真模型,对自励式磁控电抗器进行仿真分析和性能比较。分析表明:在不比现有自励式磁控电抗器复杂的条件下,新型自励式磁控电抗器的暂态响应时间缩短至现有自励式磁控电抗器的1/10以下。
磁控电抗器;仿真分析;暂态时间;性能比较
0 引言
磁控电抗器(Magnetically Controllable Reactor,MCR)是一种电抗值可以连续调节的电抗器,在电力系统中有广泛的应用[1-3]。磁控电抗器的基本工作原理是:连续调节磁控电抗器闭环铁心上直流线圈中直流电流的大小,达到连续调节闭环铁心的饱和程度,实现连续调节闭环铁心上交流线圈(电抗线圈)中过励磁电流大小,即连续调节磁控电抗器的电抗值。对磁控电抗器的研究,已经有许多成果[4-9],但是,现有的磁控电抗器的暂态响应时间较长,不能满足电力系统需求。文献[10]提出一种快速响应的磁控电抗器,该磁控电抗器是它励式磁控电抗器,它励式磁控电抗器使用不方便。文献[11]提出一种快速响应的自励式磁控电抗器,该自励式磁控电抗器的晶闸管在线圈中部,对地电压高,不能应用于超高压电力系统。文献[12]提出一种可应用于超高压电力系统的自励式磁控电抗器,但该自励式磁控电抗器的暂态响应时间仍然比较长,仍然需要改进。
本文提出一种可应用于超高压电力系统的新型的自励式磁控电抗器。利用Matlab/Simulink软件对本文与文献[12]1所提出的可应用于超高压电力系统的自励式磁控电抗器进行仿真与对比分析。
1 两种磁控电抗器的基本结构
图1(a)是文献[12]2提出的自励式磁控电抗器结构,为表述方便,称为第一种磁控电抗器。图1(b)是本文提出的新型自励式磁控电抗器,为表述方便,称为第二种磁控电抗器。图1中的1、2是磁控电抗器的两端,3是磁控电抗器闭环铁心,D1,D2是晶闸管,控制电路4控制晶闸管触发角的大小。线圈L1、线圈L2、线圈L3、线圈L4匝数相等,匝数等于同等电压等级变压器线圈匝数的1/2。线圈L5、线圈L6匝数相等,匝数与其他线圈的匝数不相等,以便晶闸管D1,D2两端获得交流电压。D3为续流二极管。
第一种磁控电抗器线圈L5、线圈L6匝数是线圈L3、线圈L4匝数的2.02倍。第二种磁控电抗器线圈L5、线圈L6匝数是线圈L3、线圈L4匝数的1.02倍。第一种磁控电抗器与第二种磁控电抗器连接方式的差别如图1(a)、(b)所示。

图1 磁控电抗器结构图
如果第一种磁控电抗器的1、2两端加额定交流电压,线圈L1、线圈L2、线圈L3、线圈L4两端的电压相等,都等于1/2额定电压,线圈L1、线圈L2、线圈L3、线圈L4流过励磁电流。由于线圈L5匝数比线圈L1、线圈L3匝数之和还多1%,所以,线圈L5两端电压比磁控电抗器1、2两端额定交流电压大1%,晶闸管D1两端有交流电压,该电压是额定电压的1%。同理,晶闸管D2两端有交流电压,该电压也是额定电压的1%。
如果晶闸管D1,D2截止,第一种磁控电抗器线圈L5、线圈L6没有直流电流,磁控电抗器闭环铁心不会饱和,磁控电抗器线圈L1、线圈L2、线圈L3、线圈L4流过的是励磁电流。第一种磁控电抗器呈现最大电抗Zmax。
如果晶闸管D1,D2被触发为全导通。第一种磁控电抗器晶闸管D1,D2构成半波整流电路,线圈L5的直流电流向下,线圈L6的直流电流向上,直流磁通在线圈L5、线圈L6所在的两铁心柱之间形成直流磁通闭环。磁控电抗器铁心出现饱和,线圈L1、线圈L2、线圈L3、线圈L4呈现较大的过励磁电流。第一种磁控电抗器呈现最小电抗Zmin。
调节晶闸管D1,D2触发角的大小,可调节线圈L5、线圈L6中直流电流的大小,从而可调节磁控电抗器铁心的饱和程度。磁控电抗器电抗值可在Zmin~Zmax之间调节、变化。实现第一种磁控电抗器电抗值的连续调节变化。
如果第二种磁控电抗器的1、2两端加额定交流电压,线圈L1、线圈L2、线圈L3、线圈L4两端的电压相等,都等于1/2额定电压,线圈L1、线圈L2、线圈L3、线圈L4流过励磁电流。由于线圈L5匝数比线圈L3匝数多2%,所以,线圈L5两端电压比线圈L3两端电压大2%,晶闸管D1两端有交流电压,该电压是额定电压的1%。同理,晶闸管D2两端有交流电压,该电压也是额定电压的1%。
如果第二种磁控电抗器晶闸管D1,D2截止,线圈L5、线圈L6没有直流电流,磁控电抗器闭环铁心不会饱和,磁控电抗器线圈L1、线圈L2、线圈L3、线圈L4流过的是励磁电流。第二种磁控电抗器呈现最大电抗Zmax。
如果第二种磁控电抗器晶闸管D1,D2被触发为全导通。晶闸管D1,D2构成半波整流电路。从图1(b)可以看出,线圈L5的直流电流向下流,线圈L6的直流电流向上流。从图1(b)可以看出,线圈L5的直流电流向下流,线圈L2的直流电流也向下流,但是,由于线圈L3的旁路作用,线圈L5的直流电流与线圈L2的直流电流的大小不相等。线圈L6的直流电流向上流,线圈L1的直流电流也向上流,但是,由于线圈L4的旁路作用,线圈L6的直流电流与线圈L1的直流电流的大小不相等。线圈L1的直流电流的流通方向与线圈L5的直流电流的流通方向相反,线圈L1与线圈L5处于同一铁心柱上,所以,线圈L5直流电流在铁心柱中产生的磁通被线圈L1直流电流产生的磁通抵消一部分,还剩余一部分。同理,线圈L2的直流电流的流通方向与线圈L6的直流电流的流通方向相反,线圈L2与线圈L6处于同一铁心柱上,所以,线圈L6直流电流在铁心柱中产生的磁通被线圈L2直流电流产生的磁通抵消一部分,还剩余一部分。剩余的直流磁通在线圈L5、线圈L6所在的两铁心柱之间形成直流磁通闭环。磁控电抗器铁心柱出现饱和,线圈L1、线圈L2、线圈L3、线圈L4呈现较大的过励磁电流。第二种磁控电抗器呈现最小电抗Zmin。
调节第二种磁控电抗器晶闸管D1,D2触发角的大小,可调节线圈L5、线圈L6中直流电流的大小,从而可调节磁控电抗器铁心的饱和程度。磁控电抗器电抗值可在Zmin~Zmax之间调节、变化。实现第二种磁控电抗器电抗值的连续调节变化。
2 磁控电抗器的仿真分析
2.1暂态响应时间仿真分析
首先研究分析10 kV磁控电抗器,积累经验后再研究分析更高电压等级的磁控电抗器。
用Matlab/Simulink构建第一种磁控电抗器仿真模型,如图2所示。仿真模型参数:T1变压器容量为577 kVA,E1为10 000 V;线圈L1电压为5 000 V,线圈L2电压为5 000 V,线圈L3电压为5 000 V,线圈L4电压为10 100 V。T1变压器的规格参数与T2变压器相同。
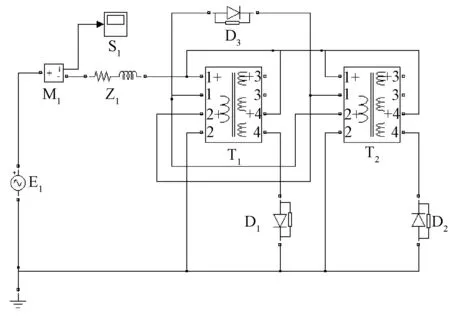
图2 第一种磁控电抗器Simulink仿真模型
不难看出,在上述参数下第一种磁控电抗器晶闸管D1,D2两端交流电压等于100 V。
为了突出主要问题,也为了研究方便,本文在晶闸管D1,D2被触发成全导通状态的条件下,分析研究磁控电抗器的特性。这样,图1所示磁控电抗器中的晶闸管D1,D2用二极管D1,D2代替。
对图2仿真模型进行仿真实验,电流测量示波器S1显示的电流波形如图3所示。从图3可以观察到,第一种磁控电抗器的电流波形峰值为200 A,暂态响应时间1.4 s。
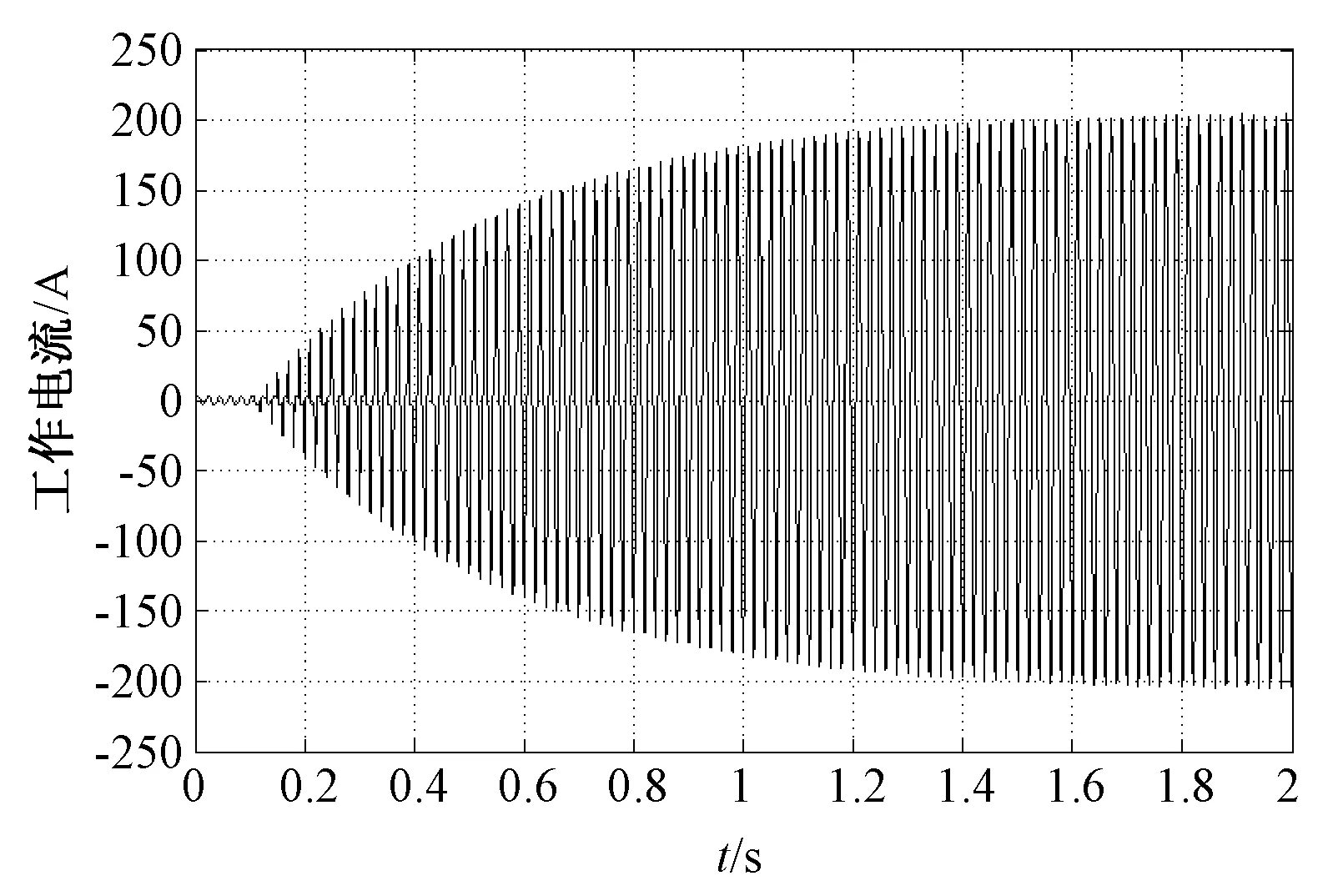
图3 第一种磁控电抗器仿真实验电流波形
用Matlab/Simulink构建第二种磁控电抗器仿真模型,如图4所示。仿真模型参数:T1变压器容量为577 kVA,E1为10 000 V;线圈L1电压为5 000 V,线圈L2电压为5 000 V,线圈L3电压为5 000 V,线圈L4电压为5 100 V。T1变压器的规格参数与T2变压器相同。
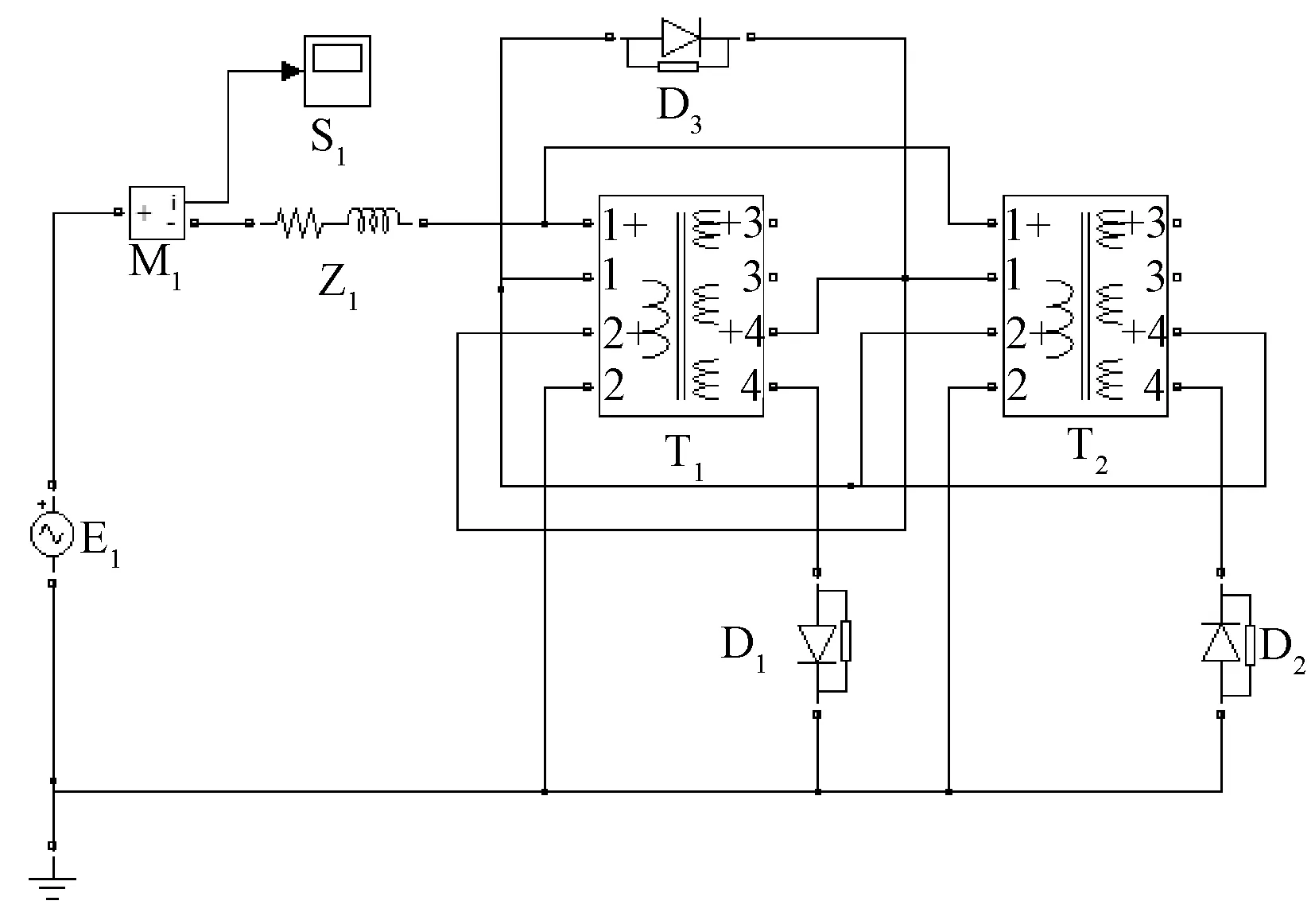
图4 第二种磁控电抗器Simulink仿真模型
不难看出,在上述参数下第二种磁控电抗器晶闸管D1,D2两端交流电压与第一种磁控电抗器晶闸管D1,D2两端交流电压一样,都等于100 V。

图5 第二种磁控电抗器仿真实验电流波形
对图4仿真模型进行仿真实验,电流测量示波器S1显示的电流波形如图5(a)所示。从图5(a)可以观察到,第二种磁控电抗器的电流波形峰值为100 A,暂态响应时间0.14 s。
如果把图4所示仿真模型中的参数修改为:T1变压器线圈L4电压为5 350 V,T2变压器线圈L4电压为5 350 V;仿真模型的其他参数保持不变。对修改参数后的图4仿真模型再进行仿真实验,电流测量示波器S1显示的电流波形如图5(b)所示。从图5(b)可以观察到,第二种磁控电抗器的电流波形峰值为200 A,暂态响应时间0.06 s。
2.2综合分析
(1)图3与图5(a)比较。这时,第一种磁控电抗器晶闸管D1(D2)的交流电压是100 V,第二种磁控电抗器晶闸管D1(D2)的交流电压也是100 V的条件下进行的对比分析。可以观察到,第一种磁控电抗器的暂态响应时间1.4 s,第二种磁控电抗器的暂态响应时间0.14 s。第二种磁控电抗器暂态响应时间比第一种磁控电抗器缩小10倍。
(2)图3与图5(b)比较。这是第一种磁控电抗器与第二种磁控电抗器的输出电流峰值都是200 A条件下进行的对比分析。可以观察到,第一种磁控电抗器的暂态响应时间1.4 s,第二种磁控电抗器的暂态响应时间0.06 s。第二种磁控电抗器暂态响应时间比第一种磁控电抗器缩小21倍。
(3)第一种磁控电抗器的晶闸管D1,D2的交流电压是100 V条件下进行仿真,从图3可以看出,第一种磁控电抗器的输出电流峰值200 A。第二种磁控电抗器的晶闸管D1,D2的交流电压也是100 V条件下进行仿真,从图5(a)可以看出,第二种磁控电抗器的输出电流峰值100 A。第二种磁控电抗器的输出电流峰值比第一种磁控电抗器小。这是因为,第二种磁控电抗器线圈L1直流电流的流通方向与线圈L5直流电流的流通方向相反,线圈L5直流电流在铁心柱中产生的磁通被线圈L1直流电流在铁心柱中产生的磁通抵消一部分;线圈L2直流电流的流通方向与L6线圈直流电流的流通方向相反,L6线圈直流电流在铁心柱中产生的磁通被L2线圈直流电流在铁心柱中产生的磁通抵消一部分。所以,第二种磁控电抗器的输出电流峰值比第一种磁控电抗器小,符合工作原理。
(4)第二种磁控电抗器线圈L1直流电流的流通方向与线圈L5直流电流的流通方向相反, 线圈L1电流的暂态过程与线圈L5电流的暂态过程对冲;线圈L2直流电流的流通方向与线圈L6直流电流的流通方向相反, 线圈L2电流的暂态过程与线圈L6电流的暂态过程对冲。实验表明,同一铁心柱上的两线圈电流方向如果发生对冲,可减小线圈电流暂态过程。
(5)如图1(a)、(b)所示,第一种磁控电抗器与第二种磁控电抗器的晶闸管D1,D2的位置都在线圈一端。如果两种磁控电抗器线圈都采用星形连接,端子2接地,两种磁控电抗器的晶闸管D1,D2对地电压很低。两种磁控电抗器都可用于超高压、特高压电力系统领域。
(6)如图1(a)、(b)所示,第一种磁控电抗器的结构与第二种磁控电抗器的结构差别不大。第二种磁控电抗器在结构复杂程度没有增大的情况下,很大地缩小了第二种磁控电抗器的暂态响应时间。
3 结论
新型自励式磁控电抗器结构在不比现有磁控电抗器复杂的条件下,暂态响应时间缩小至现有磁控电抗器的1/10以下。
[1]雷晰,邓占锋,徐桂芝,等.磁控型可控并联电抗器研究与实践[J].中国电机工程学报,2014,34(z1):225-231.
[2]黄晓胜,史欢,田翠华,等.基于磁控电抗器的变电站无功电压控制[J]. 电力自动化设备,2011,31(8):99-102.
[3]郑海涛,郑昕,吴兴全,等.大型并网风电场和光伏电站内动态无功补偿的应用技术分析[J]. 电力系统保护与控制,2014,42(16):149-154.
[4]蔡宣三,高越农. 可控饱和电抗器——原理、设计与应用[M]. 北京:中国水利水电出版社,2008.
[5]陈柏超,陈维贤. 磁阀式可控电抗器的数学模型及特性[J].武汉水利电力大学学报,1995,28(3):293-298.
[6]刘海鹏,尹忠东,赵士硕.磁控电抗器快速性研究[J].电力电子技术,2013,47(1):15-17.
[7]田铭兴,杨雪凇,顾生杰,等.基于MATLAB的磁饱和式可控电抗器的仿真模型参数及过渡时间分析[J].电力自动化设备,2013,33(6):47-51.
[8]李晓明.几种磁控电抗器的分析与比较[J].第31届中国高校电力系统及其自动化年会论文集,2015,113-116.
[9]李晓明.新型磁控电抗器的分析与比较[J].电气技术,2016,17(3):23-26.
[10]赵士硕,尹忠东,刘海鹏.快速响应磁控电抗器的新结构与控制方法[J].中国电机工程学报,2013,33(15):149-155.
[11]裘继海,孙新年.基于Simulink的快速响应磁阀式可控电抗器研究[J].淮海工学院学报(自然科学版),2013(4):17-21.
[12]李晓明.一种新型磁控电抗器及其分析[J].华电技术,2015,37(12):1-3.
Simulation Analysis for a Self-excited Magnetically Controllable Reactor
LI Xiaoming
(School of Electrical Engineering, Shandong Univesity, Jinan 250061, China)
The magnetic control reactor(MCR) has been widely used in power system. The currently existing self-excited MCR which can be used for EHV power system are existing shortcomings of transient response time is very long, can not meet the requirement of the power system. A new self-excited MCR which can be used for EHV power system is proposed in this paper. A simulation model based on Matlab/Simulink is built, the new self-excited MCR is simulated and is compared. The results show that, new self-excited MCR structure in less complex than existing self-excited MCR conditions, the transient response time of new self-excited MCR is shorter than the existing self-excited MCR by more than 1/10.
magnetically controllable reactor;simulation analysis;transient time;performance comparison
2016-04-29。
李晓明(1956-),男,副教授,主要研究方向为电力系统保护与控制、电力系统及其自动化,E-mail:lixm@sdu.edu.cn。
TM472
A
10.3969/j.issn.1672-0792.2016.08.005

