基于模糊滑模变结构永磁同步电机的控制方法

顾华利，张海涛，狄东照，孙其东

(1. 山东科技大学 电气与自动化工程学院，山东青岛266590；2. 山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东青岛266590；3.国网山东利津县供电公司，山东东营257400)



基于模糊滑模变结构永磁同步电机的控制方法

顾华利1,2，张海涛3，狄东照1,2，孙其东1,2

(1. 山东科技大学 电气与自动化工程学院，山东青岛266590；2. 山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东青岛266590；3.国网山东利津县供电公司，山东东营257400)

永磁同步电机(PMSM)是一个典型的强耦合非线性系统，滑模控制中由于滑动阶段的不变性，其对系统参数的抗干扰能力较强，因此，在滑动阶段具有良好的鲁棒性，但滑模控制自身也存在着严重的抖振。引入边界层法，使得控制作用在边界层内部变为连续控制，边界层外为常规滑模控制，提高系统的运动性能。同时采用模糊控制器，实时在线调整滑模控制器切换变量中符号函数前的系数，减弱系统抖振。最后用MATLAB/SIMULINK建立仿真模型，在0.15 s时刻设置负载突变，仿真结果表明，模糊滑模变结构永磁同步电机系统矢量控制具有更好的鲁棒性及抗干扰能力。

永磁同步电机；模糊控制；滑模变结构控制；边界层法；小波分析

0　引言

现代交流伺服控制系统中，永磁同步电机(PMSM)以其优异的性能在航空航天、数控机床以及特种加工等领域得到了广泛的应用[1]。PMSM本身强耦合、非线性的特点使传统双闭环PI控制方式难以满足要求[2]。现代控制理论如模型参考自适应控制、神经网络控制、滑模变结构控制被逐步应用到PMSM控制系统中[3-5]。滑模控制由于滑动阶段的不变性，其对系统参数的抗干扰能力较强，得到越来越多学者的关注，并在电机的伺服控制中得到应用[6-7]。传统滑模控制器由于抖振问题的存在影响系统的稳定，对系统的整体性能造成很大影响。传统滑模控制将误差及误差导数作为输入量，但导数项会加剧系统滑模面带来的抖振，通过在传统滑模面中加入状态量的积分量，有效消除了系统误差。边界层法作为一种常用的消抖方法，该方法用饱和函数代替控制律中的符号函数，使得控制作用在边界层以内为连续的控制[8]。最后通过将模糊控制器与滑模控制器相结合[9]，改变滑模变结构控制器切换控制量中符号函数前的系数。通过小波分析表明，模糊滑模变结构控制PMSM比传统PI控制具有更好的运动性能。

1　永磁同步电机(PMSM)数学模型

为简化分析，忽略定子铁心饱和、铁心涡流、磁滞损耗及转子上的阻尼绕组等因素的影响，建立PMSM在d-q轴坐标系下的数学模型。

电压方程：

(1)

磁链方程：

(2)

对于表面式PMSM有Ld=Lq，所以转矩方程：

(3)

机械运动方程：

(4)

式中：ud，uq为d轴和q轴的定子电压；id，iq为d轴和q轴的定子电流；R为定子电阻；ψf为永磁体与定子交链出的磁链；ω为转子角速度；ψd，ψq为d轴和q轴的定子磁链；Te，TL为电磁转矩和负载转矩；P为磁极对数；J和B分别表示为电机转动惯量和摩擦系数。

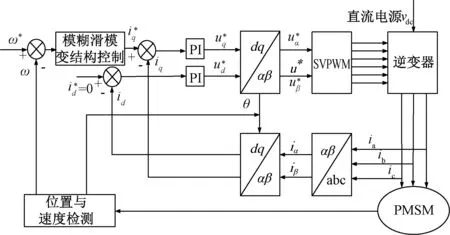
图1　永磁同步电机控制框图

2　滑模变结构控制器的设计

取PMSM控制系统的状态变量为

(5)

式中：ω*为给定电机转速；ω为实际转速。

结合式(3)、(4)，并对x1，x2求导可得

(6)

常规滑模面中包含速度误差的微分量，而这一过程容易产生高频噪声。本文在常规滑模面的基础上加入状态变量的积分量，可得系统的滑模面s为

s=x1+cx2

(7)

式中：c为积分常数，可设置为正常数。

对式(7)滑模面s求导可得

(8)

指数趋近律能在一定程度上减弱滑模抖动，在实际系统控制中，有效合理的趋近律设计可以在远离滑模面时，运动点趋向切换面的速度增大，以加快系统的动态响应；在趋近滑模面时，其速度逐渐趋近于零，从而减弱抖振。本文采用指数趋近律来设计滑模控制器，其表达式为

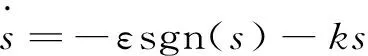
(9)

式中：ε，k均为大于零的常数。

结合式(8)、(9)可得

(10)

由式(10)可得控制量iq的表达式

(11)

为进一步减弱高频抖振对系统带来的不利影响，本文采用sloline及Sasbry提出的边界层法，即将控制器中的符号函数项用平滑的饱和函数取代，使得控制作用在边界层内部变为连续控制，饱和函数的表达式为

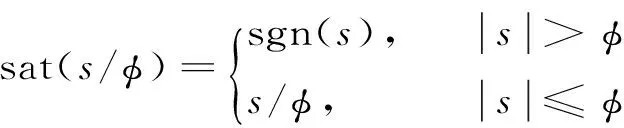
(12)

式中：φ>0为边界层厚度。

用sat(s/φ)代替控制律中的sgn(s)，则式(11)可转换为

(13)

3　二维模糊控制器的设计

如图2所示为模糊滑模变结构控制系统图，对永磁体同步电机给定转速与输出转速进行比较，将滑模面S及其导数dS/dt输入二维模糊控制器中，通过模糊控制器实时调整ε(s)的值，输出的ε(s)经过比例因子h量化来实时调整滑模控制器中ε值的大小，使系统具有良好的动态性能。

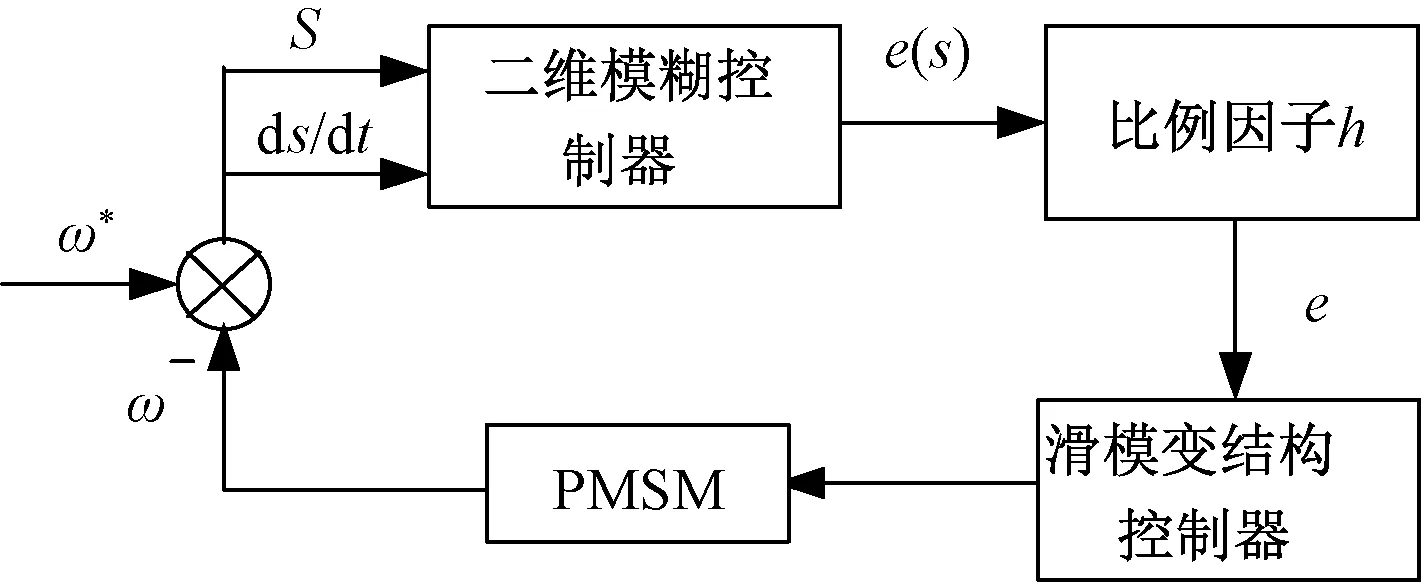
图2　模糊滑模变结构控制系统图

由公式(9)可知滑模控制器的输出量有等效控制量和切换控制量组成，切换控制量中符号函数前的系数ε决定着系统到达滑模面的速度和在滑动阶段抖振的强弱。系数ε过大，则到达滑模面的时间短，但在滑动阶段抖振会增强；系数ε过小，可减弱滑动阶段的抖振，但到达滑模面的时间变长。因此ε的取值对系统的性能产生直接影响。

图3所示，ε(s)含7个模糊子集{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)},连续性论域为[-3,3]。模糊控制器中输入量和输出量均采用三角形隶属函数，去模糊化时采用加权平均法。应用IF A AND B THEN C 模糊规则，然后根据MIN-MAX重心法求输出变量。 模糊规则建立的依据是系统状态点距离滑模面的远近程度，根据实际操作过程中的经验，当系统状态轨迹远离滑模面，即s和ds取值较大时，ε(s)应取较大值，加快响应速度；系统状态轨迹靠近滑模面时，ε(s)应取较小值。因此，可获得表1所示的模糊规则表。

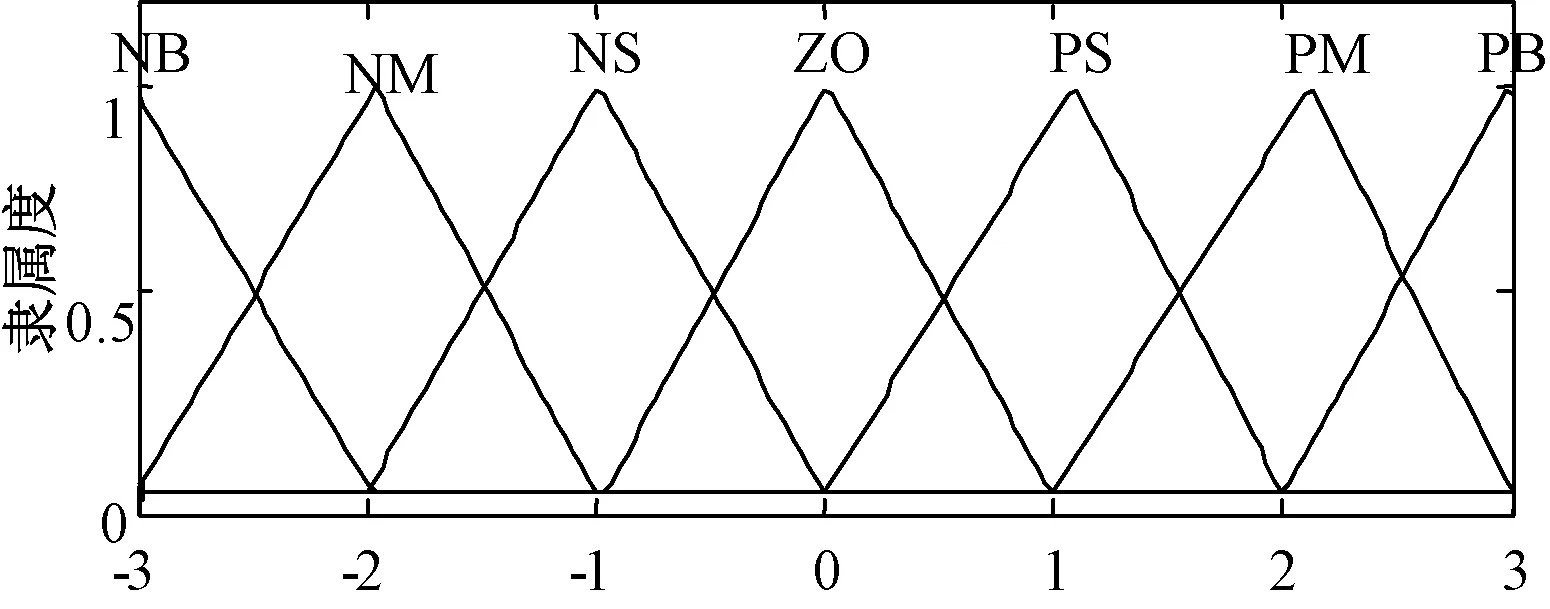
图3　隶属度函数

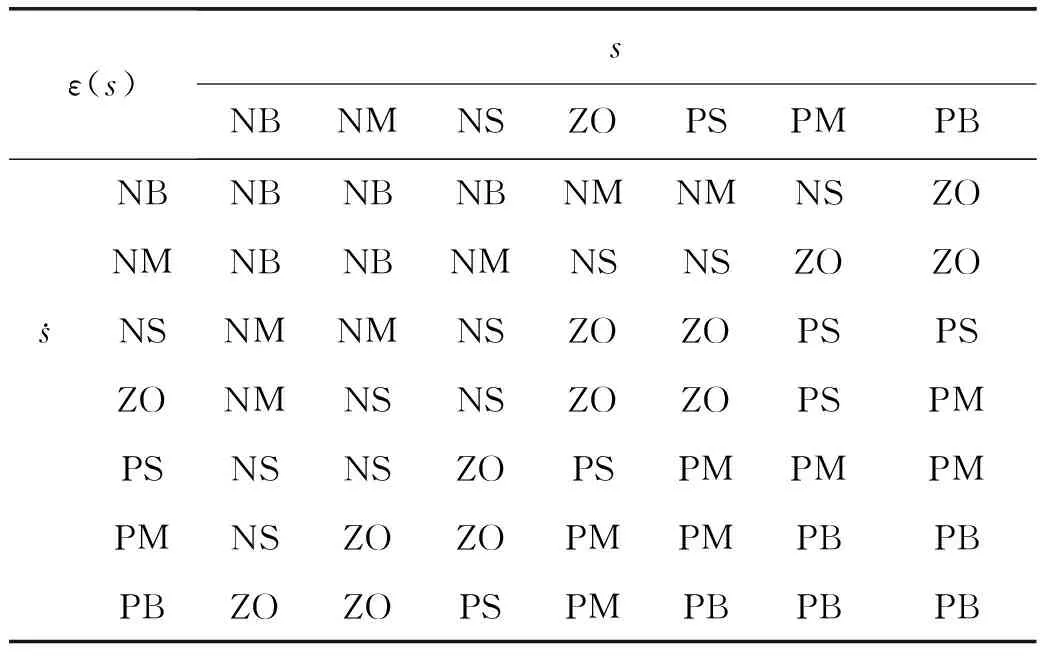
ε(s)sNBNMNSZOPSPMPBNBNBNBNBNMNMNSZONMNBNBNMNSNSZOZsNSNMNMNSZOZOPSPSZONMNSNSZOZOPSPMPSNSNSZOPSPMPMPMPMNSZOZOPMPMPBPBPBZOZOPSPMPBPBPB

4　仿真实验结果

为验证所提控制策略的有效性，采用MATLAB/SIMULINK分别搭建传统双闭环矢量控制系统和模糊PI矢量控制系统仿真模型进行对比。仿真中采用的表贴式永磁同步电机的参数为：定子电阻Rs=2.875 Ω；直轴电感和交轴电感Ld=Lq=8.5 mH;转子磁链ψf=0.175 Wb；电动机转动惯量J=0.008 kg·m2；摩擦系数B=0.001 kg·m2/s；磁极对数np=4。负载转矩TL=2 N·m。系统仿真时间为0.2 s，给定转速为600 r·min-1，在0.15 s时突加负载由4 N·m变为10 N·m。

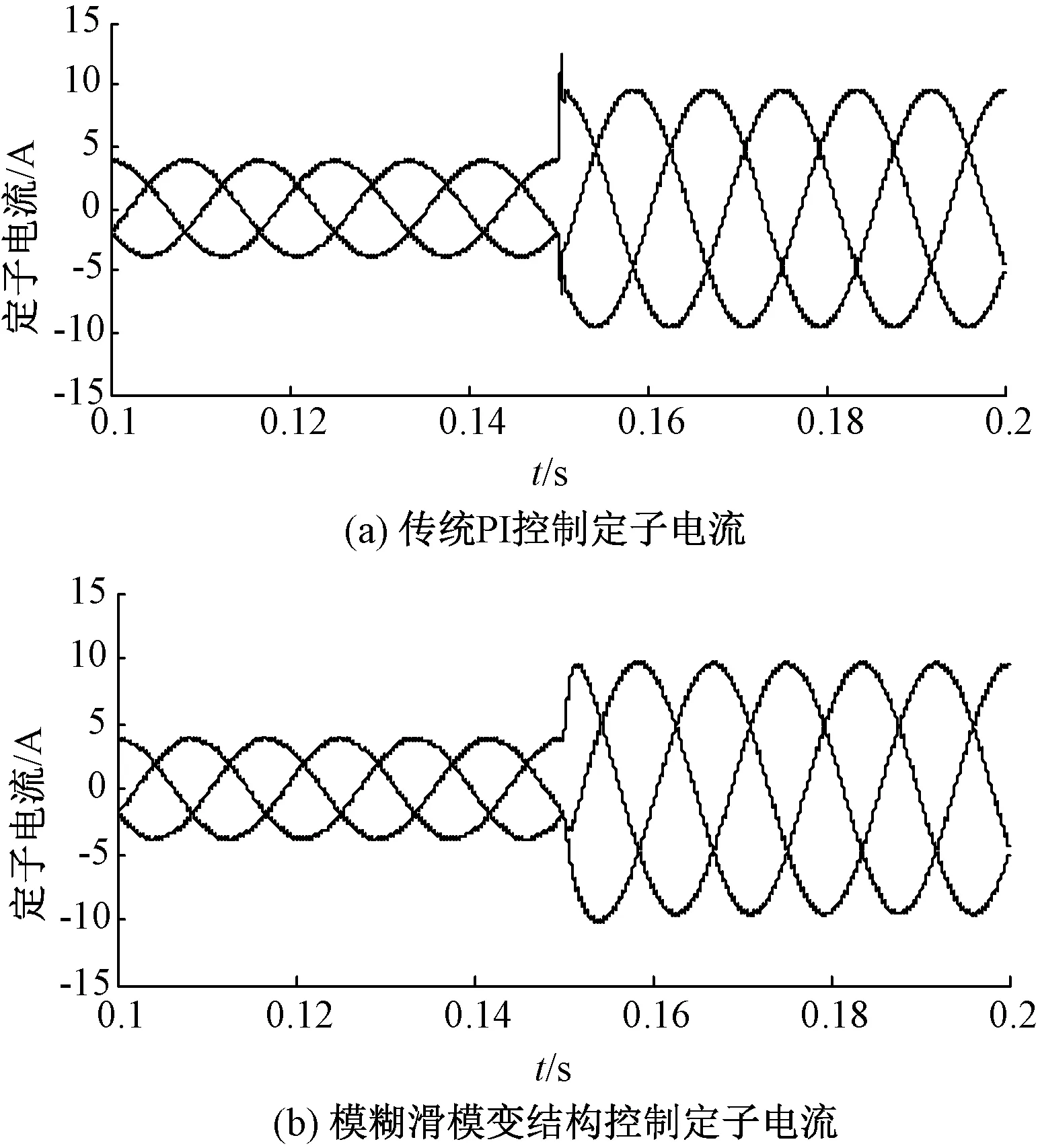
图4　三相定子电流

图4为突加负载时传统PI控制与模糊滑模变结构控制下系统三相定子电流波形，从图4中可以看出，模糊滑模变结构定子电流过度更平稳，当系统稳定运行时，可以实现电流波形正弦化。

图5为电磁转矩波形，可以看出当突加负载时系统在变结构控制下可以平稳地运行到稳定状态，扰动对系统的影响较小。传统PI控制下电磁转矩响应迅速，但其超调量较大，影响系统的稳定运行。

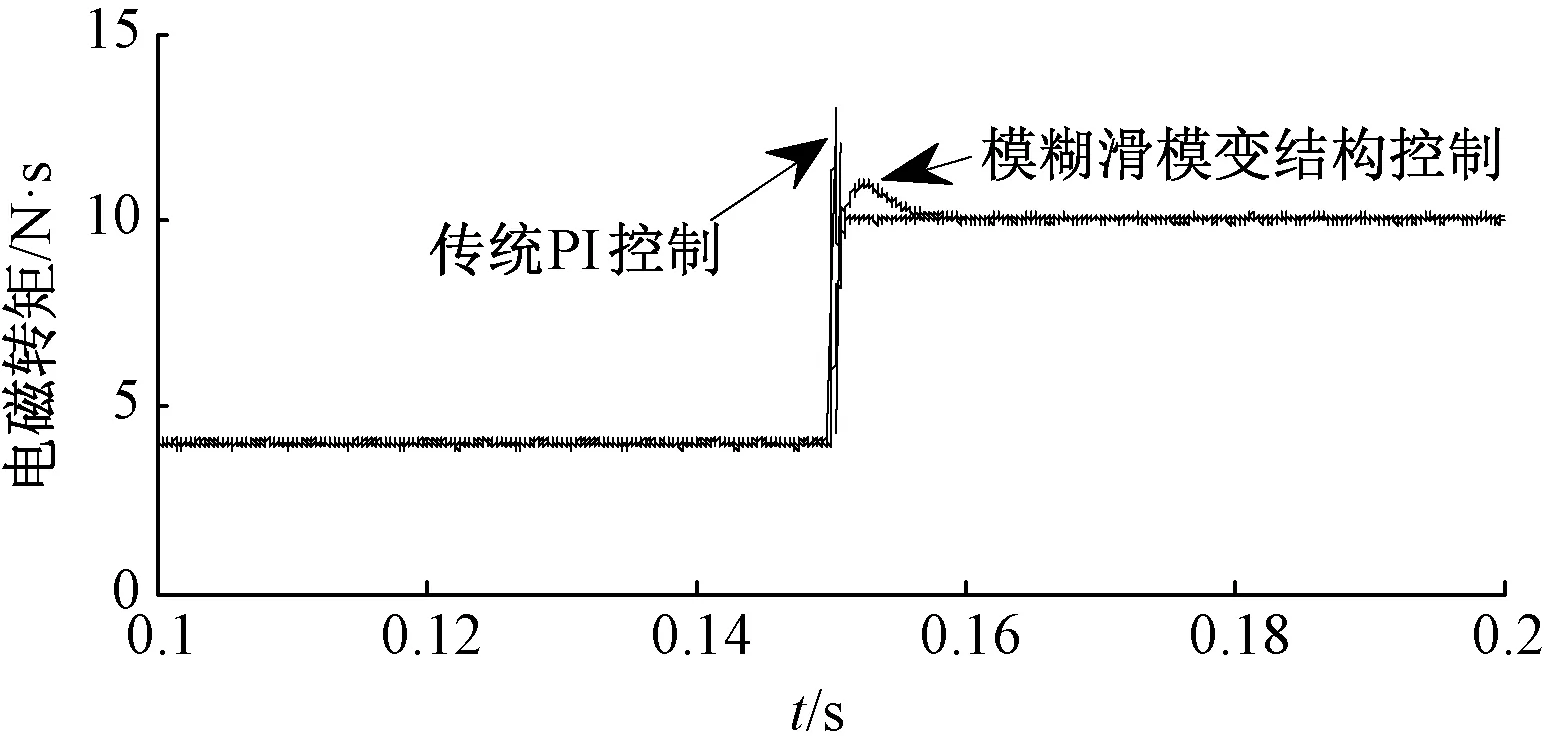
图5　电磁转矩

图6为系统转速整体波形，图7为转速的超调量与波动量波形图。在传统PI控制下，系统启动存在超调，并有一定的超调时间；而在模糊滑模控制下，系统能较快无超调地达到给定转速，可以提前4个基波周期达到稳定状态。当0.15 s负载转矩发生突变时，传统PI控制输出转速波动较大，0.155 s时恢复到稳定状态，恢复时间相当于5个基波周期；模糊滑模变结构控制方式转速波动较小，0.153 s时恢复到稳定状态，恢复时间相当于3个基波周期，比传统PI控制提前2个基波周期到达稳定状态。

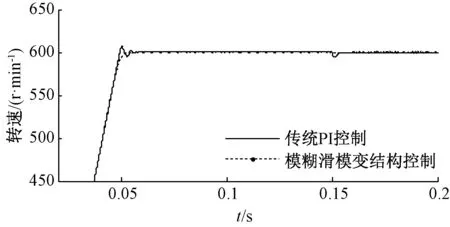
图6　转速波形

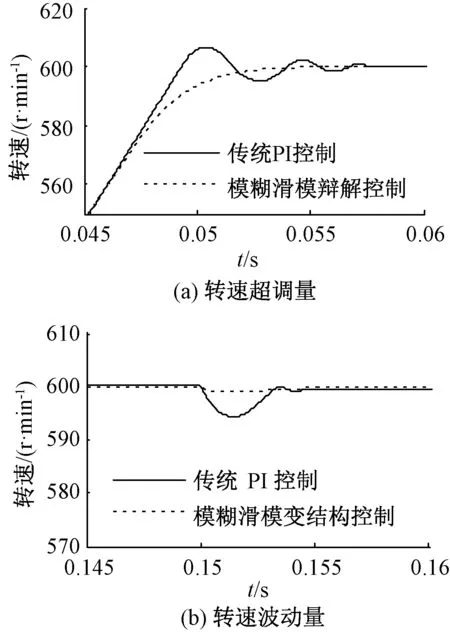
图7　转速波形对比

进一步比较两种控制方式，采用sym8小波5层分解[10]。将速度波形导入到Matlab主窗口workspace中，在主窗口中调用小波分析工具箱对导入数据进行处理，对转速波形进行5层分解并抽取数据。小波抽取数据来分析两种控制方式的运行结果，如表2所示。

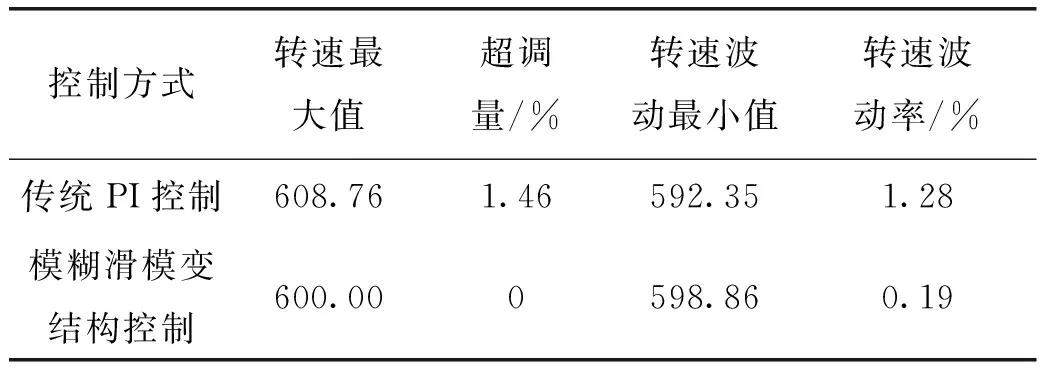
表2　两种控制方式的转速数据对比

系统输出转速的给定稳态值为600，由表2可知，传统PI控制转速超调量为1.46%小于10%，且从图3中可以看出到达稳定转速的时间小于0.1 s，均满足控制系统性能指标。而模糊滑模变结构控制可以实现无超调，可以更好地满足系统的性能。当突加负载时，传统PI控制器中的参数固定，不能根据负载的变化来调整动态性能，转速波动率为1.28%，而模糊滑模变结构控制方式仅为0.19%，可以看出，模糊滑模变结构控制方式抗干扰能力较强。

5　结论

本文采用模糊滑模变结构控制方法，利用滑模控制能够快速无超调的响应给定转速，提高了电机启动时的性能。利用模糊控制实时在线调整滑模控制器切换变量中符号函数前的系数ε，使永磁同步电机在运行过程中具有自整定性。最后，通过仿真实验证明了该滑模变结构控制相比于传统PI控制具有更好的鲁棒性和抗干扰能力。

[1]陆华才, 徐月同, 杨伟民, 等. 永磁直线同步电机进给系统模糊PID控制[J]. 电工技术学报, 2007, 22(4): 59-63.

[2]樊英杰, 张开如, 韩璐,等. 基于优化SVPWM永磁同步电机的研究[J]. 煤矿机械, 2015(8):80-83.

[3]罗慧, 尹泉, 孙明明. 交流伺服系统参数辨识方法综述[J]. 伺服控制, 2012(1):27-29.

[4]柴天佑, 丁进良, 王宏,等. 复杂工业过程运行的混合智能优化控制方法[J]. 自动化学报, 2008, 34(5):505-515.

[5]樊英杰, 张开如, 马慧,等. 基于模糊PI永磁同步电机优化矢量控制系统的研究[J]. 电气传动, 2016, 46(3):15-19.

[6]马立新, 范洪成, 徐镇乾,等. 基于惯量辨识PI自整定永磁伺服电机控制[J]. 电力科学与工程, 2015(9):28-32.

[7]童克文, 张兴, 张昱,等. 基于新型趋近律的永磁同步电动机滑模变结构控制[J]. 中国电机工程学报, 2008, 28(21):102-106.

[8]李乙杰, 李锐华, 孙耀杰,等. 基于边界层法的电磁轴承滑模变结构控制研究[J]. 系统仿真学报, 2005, 17(8):1962-1965.

[9]刘明基, 郭韩金, 舒佳驰. 基于SVPWM技术的永磁同步电机模糊自适应控制系统研究[J]. 电力科学与工程, 2013, 29(2):11-14.

[10]周伟. 基于MATLAB的小波分析应用[M]. 西安：西安电子科技大学出版社, 2010.

Control Methord of Permanent Magnet Cynchronous Motor Based on Fuzzy Sliding-mode Variable Structure

GU Huali1,2，ZHANG Haitao3，DI Dongzhao1,2，SUN Qidong1,2

(1. College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao 266590, China; 2. State Key Laboratory of Mining Disaster Prevention and Control Co- founded by Shandong Province and the Ministry, Shandong University of Science and Technology, Qingdao 266590, China; 3.State Grid Lijin Power Supply Company,Dongying 257400,China)

Permanent magnet synchronous motor (all-digital fuzzy) is a typical system with strong coupling nonlinear characteristics. Due to the sliding phase invariability in the sliding mode control, it owns better anti-interference ability against system parameters, so the sliding phase has good robustness, but the sliding mode itself has the serious problem of buffeting. Boundary layer method is introduced so that control action within the boundary layer becomes continuous, whereas outside the boundary layer using conventional sliding mode control, so that the motion performance of the system is improved. By introducing the fuzzy controller at the same time and adjusting the real-time online coefficient of the sliding mode controller switching variable symbol function, the system chattering is weakened. Finally, a simulation model is built in MATLAB/SIMULINK, by setting a load mutation in the moment 0.15 s. The simulation results show that the permanent magnet synchronous motor vector control system of the fuzzy sliding mode variable structure has better robustness and anti-interference ability.

permanent magnet synchronous motor; fuzzy control; the sliding-mode variable structure control; boundary layer method; wavelet analysis

2016-04-30。

山东科技大学研究生创新基金(YC140337)。

顾华利(1990-)，男，硕士研究生，研究方向为电力系统及其自动化，E-mail：826251156@qq.com。

TM341

A

10.3969/j.issn.1672-0792.2016.08.002