基于多尺度滤波器的汽温控制前馈信号的选取

洪雨楠，刘鑫屏，王　桐

(华北电力大学 控制与计算机工程学院，河北保定071003)



基于多尺度滤波器的汽温控制前馈信号的选取

洪雨楠，刘鑫屏，王桐

(华北电力大学 控制与计算机工程学院，河北保定071003)

联络线调度模式下火电机组AGC(自动发电控制)指令复杂多变，火电机组负荷波动频繁，导致过热、再热汽温控制品质变差。引入前馈控制能够有效克服扰动，但难点在于如何选取合适的前馈信号。采用多尺度滤波器，先对各信号进行多尺度分解，再分析不同尺度间信号的相关性，通过比较不同频率尺度下信号间的相关系数，选取合适的汽温控制前馈信号。对某600 MW机组历史数据进行数据分析，表明基于多尺度滤波器的相关分析方法可以有效地挖掘信号在高频和低频的波动相关性，选取合适的汽温前馈信号。

汽温控制；前馈信号；多尺度分解；相关分析

0　引言

AGC(自动发电控制)指令复杂多变、火电机组负荷波动频繁，导致过热、再热汽温控制品质变差，影响机组运行的安全性与经济性。传统的反馈控制，只有出现扰动情况导致汽温出现偏差之后才会作用，汽温控制系统的被控对象具有大迟延、大惯性的特点，控制输出反映到被控参数的变化上需要经历很长的时间；而前馈控制在扰动出现时即可施加控制作用，具有实时性好、不影响系统稳定性的优点。

前馈-反馈汽温控制的难点在于如何选取合适的前馈信号[1]。目前研究大都是根据信号在频域变化特性的不同[2]，直接计算相关系数来衡量它们在低频成分之间的相关性强弱，实际上热工信号往往在不同频率成分之间表现出不同的相关度，为有效选取合适的汽温前馈信号，需要研究一种区分信号在不同频率相关性的分析方法。

多尺度分析(Multi-Scale Analysis，MSA)是一种新的变换分析方法[3]，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，因此十分适用于汽温控制前馈信号的寻找。基于多尺度分析的基本思想，设计了一种多尺度滤波器，对原本直接计算相关性差的信号，进行多层分解和重构，再计算它们在不同频率下的相关系数，比较信号在不同频率尺度下的相关系数，挖掘出相关性强的信号分量作为汽温控制的前馈信号。

1　理论分析

1.1多尺度滤波器基本理论

设有L2(R)空间的子空间序列：

(1)

现给出尺度方程如式(2)和式(3)：

(2)

(3)

式中：l(n)为低通滤波器；h(n)为高通滤波器，且h(n)=(-1)n·l(1-n)；φ(x)和ψ(x)分别为尺度函数和小波函数，且它们通过伸缩平移后可以构成Vj的正交基。

那么对于一个原始信号，它的多尺度分解为：

(4)

对式(4)整理得：

(5)

多尺度分析实际上是建立在函数空间概念上的理论。它构造了一组正交基，使得尺度空间与小波空间相互正交；随着尺度由大到小的变换，可以在各尺度上由粗及精地观察目标信号。由于连续小波变换在时间-尺度空间域上仍然具有冗余性[4]，故实际中通常采用离散小波变换进行分析。下面给出基于多尺度分析的一维Mallat快速算法[5]，如式(6-7)所示:

(6)

(7)

多尺度滤波器的实现原理，可以理解为一组镜像滤波的过程，即信号通过一个分解高通滤波器和分解低通滤波器。高通滤波器输出对应信号的高频分量部分，称为细节分量；低通滤波器输出对应信号的相对较低频率部分，称为近似分量，重复使用一组高通滤波器和低通滤波器对时间序列进行逐层分解，即构成多尺度滤波器。其实现过程如图1所示，原始信号序列x(n)依次通过三层多尺度分解得到不同尺度下的低频分量系数和高频分量系数。

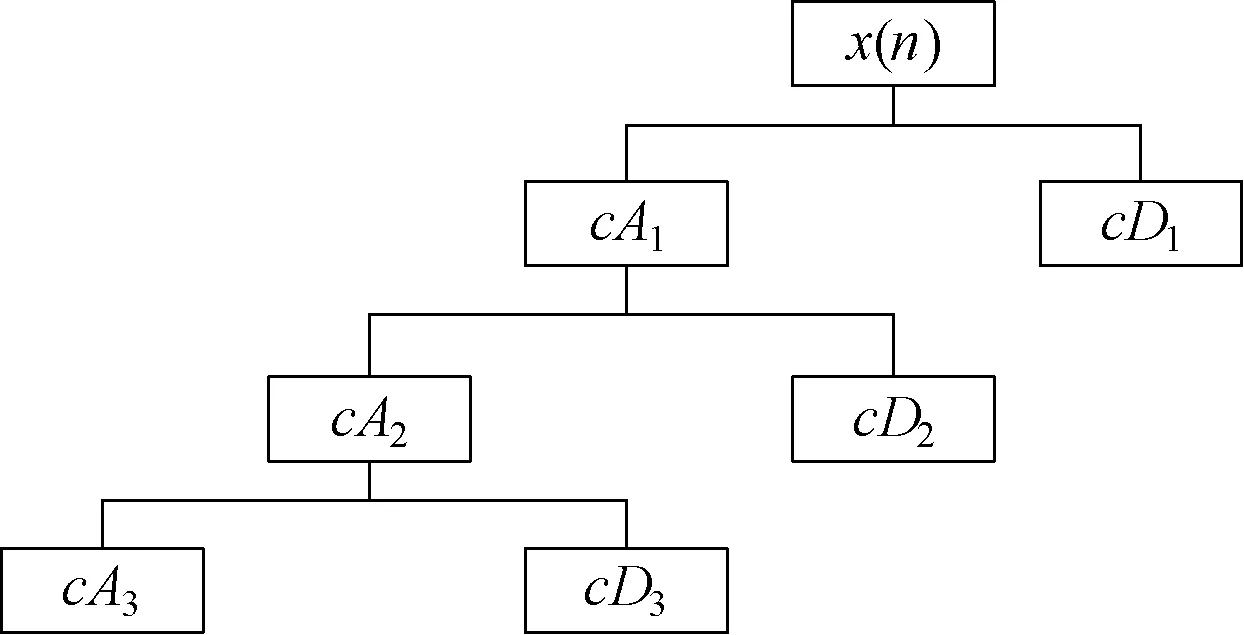
图1　多尺度滤波分解图

1.2相关分析

相关分析技术是一种常用的信号处理方法[6]，在电力系统领域已有广泛应用，一般采用皮尔逊相关系数来比较信号之间的紧密程度[7]。

设X和Y是两组能量有限的零均值信号，则它们的皮尔逊相关系数为：

(8)

RXY在(0,1)之间表示正相关，(-1,0)在之间为负相关；等于1为完全正相关，等于-1为完全负相关，等于0表示完全不相关。

1.3基于多尺度滤波器的相关分析

火电厂汽温控制系统中物质流和能量流的波动变化经测量传感器以信息流的形式呈现[8-10]，反映在测量数据中表现为波动相似性。而实际测量数据往往具有多尺度特性[11-12]，观测尺度不同，实际测量数据中包含的有效信息频率成分也不一样，数据之间的波动相似性也可能存在较大差异。因此考虑采用多尺度滤波器来寻找合适的汽温控制系统前馈信号，并通过求取相关系数来分析其相关性。

利用多尺度滤波器的多分辨率分析特性，将原始信号分解成不同频率的信号分量，再计算不同频段信号分量之间的相关系数，通过比较相关系数，便可以从海量的相关数据中找出与汽温数据信号波动相似性最强的前馈信号。基于多尺度滤波器的相关分析基本流程为：对于实际测量数据信号矩阵X(n)和Y(n)，首先通过多尺度滤波器进行时间序列分解，得到实际数据信号的近似分量A11和A21，细节分量D11，D12，…，D1m和D21，D22，…，D2m(m为分解尺度)，然后分别对A11和A21，D11和D21，…，D1m和D2m进行相关分析，依据相关系数的大小，提取出最合适的前馈信号，其实现过程如图2所示。

图2　多尺度滤波器相关分析流程图

2　数据分析

2.1原始数据信号常规相关性分析

选取某600 MW机组一段升负荷工况下的运行历史数据，从测点表中选取7个有代表性的测点，分别是发电负荷(S1)、汽包压力(S2)、主蒸汽流量(S3)、风量(S4)、氧量(S5)、给水温度(S6)和一级减温器入口汽温(S7)；直接分析它们与一级过热器出口汽温(S8)的相关性，图3给出各测点原始数据曲线，从图中可以看出发电负荷、汽包压力等7个测点原始数据信号与一级过热器出口汽温之间的相关性很差。

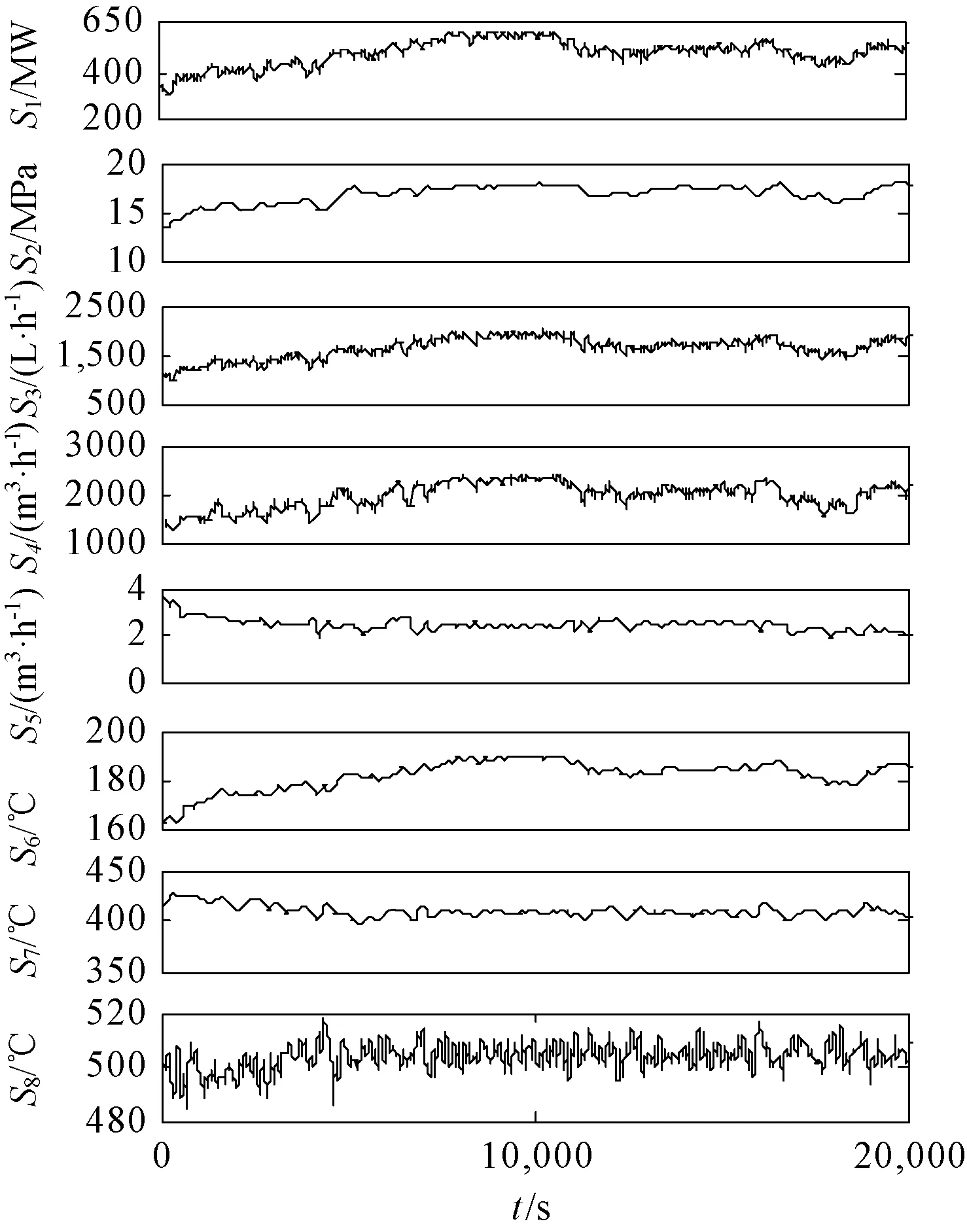
图3　原始数据曲线

直接计算它们与一级过热器出口汽温的相关系数如表1，表1中S1，S2，…，S8表示测点编号。从表1中可以发现，发电负荷等测点原始信号与一级过热器出口汽温之间的相关系数最高只能达到0.45，相关性不高。

表1　原始数据常规相关分析结果

2.2基于多尺度滤波器的数据信号相关分析

依旧选取在原始数据信号常规相关性分析中的机组历史数据，分析这些信号在不同频率尺度上的相关性。首先将发电负荷、汽包压力等7个测点数据信号进行3层多尺度滤波分解，经多尺度滤波器分解后与一级过热器出口汽温的对比曲线如图4所示。图中各信号分量用dij来表示，其中i=1，2，3，4表示第i层信号分量，j=1，2，…，7表示测点编号。这里多尺度滤波分解尺度的选择方法：首先根据数据长度和小波阶数估计理论最大分解层；然后对数据进行频谱分析，根据数据的频率范围并结合小波函数和尺度函数的中心频率确定最终分解层。

从图4(a)～(g)发现，经过多尺度滤波器分解后，原本直接计算相关性差的信号在某种尺度下的高频部分表现了很强的波动相似性，例如图4(c)中主蒸汽流量与一级过热器出口汽温在第二层高频分量之间存在较强的波动相似性，图4(e)～(f)氧量和给水温度与一级过热器出口汽温在第二层高频分量都有很强的波动相似性，尤其图4(g)一级减温器入口汽温与一级过热器出口汽温在第一层高频和第二层高频分量上都表现了很强的波动相似性。但靠肉眼观察是无法精确比较不同信号分量之间的波动相似性强弱关系；因此，计算一级过热器出口汽温与发电负荷、汽包压力等7个测点信号分解后各层分量之间的相关系数，计算结果如表2所示，为方便对照，将原始数据信号常规相关性分析的结果也列入表中。

表2中S1，S2，…，S8表示测点编号，d1，d2，d3和d4分别表示信号分解后的第一、二、三高频分量和第四层低频分量。通过对比表2中第一列和第二列的数据可知，原始数据直接进行相关分析的计算结果与多尺度分解后相关分析的第四层低频分量计算结果几乎相同，表明多尺度滤波分解能够有效地保证数据信号的整体波动趋势；而一些信号在某种高频尺度下与一级过热器出口汽温信号的相关系数达到了0.7以上，例如发电

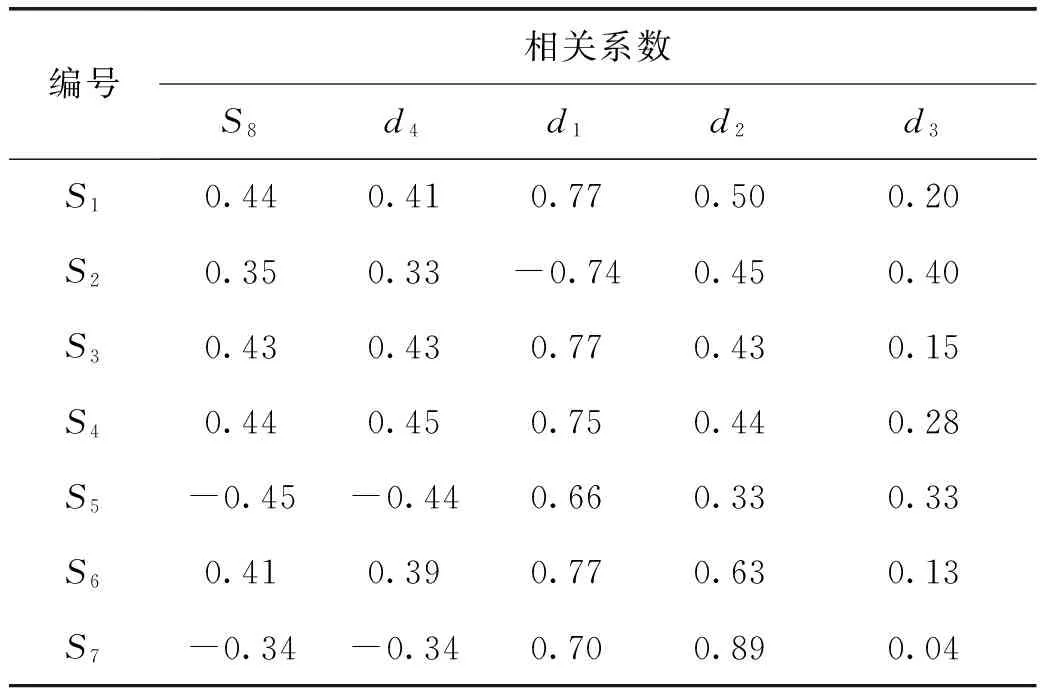
表2　多尺度分解后相关分析结果比较

负荷、汽包压力、主蒸汽流量、风量、给水温度和一级减温器入口汽温与一级过热器出口汽温的第一层高频分量；尤其一级减温器入口汽温与一级过热器出口汽温的第二层高频分量之间的相关系数R达到了0.89，明显高于发电负荷、汽包压力等其他信号分量之间的相关系数，更远超过直接进行相关分析所得的相关系数，表现了很强的波动相似性。

通过机理分析一级减温器入口汽温与一级过热器出口汽温在第二层高频的这种高相关性，分析如下：从汽水流程上看，蒸汽依次流过本级减温器入口测点、喷水减温器、导前区测点和本级过热器出口汽温测点，当本级减温器入口汽温变化时，本级过热器出口汽温必然会随之改变，但汽温投入自动后，这种相关性会变弱；另外，本级过热器入口汽温反映上级过热器受热面吸热量，本级过热器出口汽温反映本级过热器受热面吸热量，两级过热器受热面吸热量存在相关性，导致本级减温器入口汽温与本级过热器出口汽温存在高频相关性。

3　结论

(1)基于多尺度滤波器的相关分析方法能够在保证数据信号整体波动趋势的前提下，实现信

号在多个尺度的分解与重构，充分、有效地挖掘信号低频和高频分量之间的相关性。

(2)一级减温器入口汽温与一级过热器出口汽温在第二层高频相关，相关系数为0.89，选取一级减温器入口汽温作为汽温控制系统的前馈信号。

[1]王振，张红军，刘长远，等.基于负荷前馈补偿的主汽温串级广义预测控制[J].石油化工自动化，2012，48(6)：36-39.

[2]袁世通.1000 MW超超临界机组建模理论与方法的研究[D].北京：华北电力大学，2015.

[3]郝祖龙，刘吉臻，常太华，等.基于小波变换的热工信号多尺度相关性分析[J].中国电机工程学报，2010，38(14)：109-114.

[4]丁莉，陈玮青. 提升小波变换算法的分析与研究[J]. 自动化与仪器仪表息，2016，199(5)：179-180.

[5]兰华，李兰. Mallat算法与单子带重构算法的分析比较[J]. 科技与创新，2015(24)：17-18.

[6]唐慧. 云计算大数据运行控制技术对智能配电网影响的评价研究 [J].电力科学与工程，2016，32(4)：32-35.

[7]梁吉业，冯晨娇，宋鹏.大数据相关分析综述[J].计算机学报，2016，39(1)：1-18.

[8]姚立坤.300MW火电机组过热汽温控制系统优化研究[D].保定：华北电力大学，2012.

[9]丁普秀.300MW机组过热汽温系统的建模与控制算法的研究[D].保定：华北电力大学，2012.

[10]冯美方，吴恒运，房方.超超临界二次再热机组过热汽温模型辨识[J]. 华北电力大学学报(自然科学版)，2016，43(1)：76-80.

[11]张青月，王东风.基于扩展状态观测器的过热汽温控制[J].华北电力大学学报(自然科学版)，2016，43(1)：86-91.

[12]田亮，刘鑫屏，王琪，等.基于多尺度相关和机理建模的炉膛压力分析[J].动力工程学报，2012，32(11)：853-858.

Selection of Feed-forward Signal for Steam Temperature Control System Based on Multi-Scale Filter

HONG Yunan， LIU Xinping， WANG Tong

(School of Control and Computer Engineering，North China Electric Power University， Baoding 071003， China)

The AGC (Automatic Generation Control) instruction on the tie-line dispatching mode of the thermal power plant is complex and volatile. The frequently fluctuating unit load can cause the overheated situation and deteriorated quality of the reheated steam temperature control system. The feed-forward control scheme can overcome the disturbance effectively, but it is difficult to find a suitable feed-forward signal. Firstly, by using the multi-scale filter, the original signals were decomposed into components with different frequency. And then the correlation of signals in different scale was analyzed. Based on the comparison of the correlation coefficient of signals between different frequency scales, the suitable feed-forward signal for steam temperature control system was selected. The analysis on the actual data of a 600 MW unit shows that correlation analysis method of multi-scale filter can deeply analyze the fluctuation correlation of signals in high and low frequency range, and can provide the suitable feed forward signal for steam temperature control system.

steam temperature control; feed-forward signal; multi-scale decomposition; correlation analysis

2016-06-06。

国家重点基础研究发展计划项目(973 计划)(2012CB215200)；中央高校基本科研业务费专项资金资助(2014MS145)。

洪雨楠(1993-)，男，硕士研究生，研究方向为数据融合与模式识别，E-mail：331035069@qq.com。

TP273

A

10.3969/j.issn.1672-0792.2016.08.011