双驱动变杆长杆机构研磨机与ADAMS仿真研究

尹 烁 尹明富 赵镇宏

(天津工业大学机械工程学院，天津300387)

近年来，对于四杆机构的研究不再局限于连杆上某点的速度、加速度轨迹曲线的研究。更多地倾向于研究机构运动的平稳性与四杆机构的最优化设计。但从整体效果来看，由于机构运动精度受到的影响因素较多，因而其最终的运动状态不能很好地满足市场需要。

四杆机构的研究方法有图谱法、实验综合法和解析法。随着对机构运动精度要求的提高，解析法越来越受到人们的重视，使用频率也越来越高[1]。为了完成对四杆机构的运动分析，采用ADAMS软件进行仿真优化。

通常情况下，人们将四连杆机构的轨迹归纳为水滴形、卵形、椭圆形、镰刀形、8字形和弯月形等6种形状[2]。在研磨过程中，为了达到最佳研磨效果，依据不同的研磨需求，选择合适的研磨盘硬度、研磨速度、磨料粒度。在实际使用过程中发现，研磨轨迹越复杂，越有助于提高研磨的最终精度。

1 研磨运动分析

1.1 行星齿轮研磨机运动分析

现在工业应用中最多的是行星式研磨机，在行星轮系的基础上，合适的机械结构能够满足研磨运动的基本要求[3]：研磨轨迹具有时变性，即研磨速度大小基本保持不变，但方向始终在变化，并且研磨的速度分布相对比较均匀，加工效果良好。其基本原理图如图1所示。

1—齿圈 2—行星轮 3—研磨工位 4—研磨盘 5—太阳轮 6—系杆图1 行星齿轮研磨运动原理图Figure 1 Grinding motion principle of planetary wheel

根据图1所示的运动简图，在行星轮系中，周转轮系的运动关系为：

从而得到：

已知行星轮系的太阳轮、行星轮以及行星架的齿轮是相互啮合的齿轮，因此他们的模数相同，设该模数为m，则可得到：

z1=2mR

z2=2mr

z3=m(R+2r)

由此可以得到：

由上面公式可以得到通过改变太阳轮和行星轮的齿数，可以得到不同的传动比，得到的研磨曲线也是不同的。通常按照得到的轨迹曲线区分，可以分为泛外曲线，包括普通外摆线(长幅外摆线和短幅外摆线)和泛内摆线(普通内摆线、长幅内摆线和短幅外摆线)。在实际应用中，可以根据不同使用要求，通过组合行星轮系的传动比，找到最合理、经济、高效的加工方案[4]。

在实际的使用过程中，为了使研磨轨迹曲线变得复杂，提高研磨精度，文献[5]中提到，给中心轮一个偏心距，从而实现研磨曲线的复杂化。

利用MATLAB通过改变行星轮系传动比，对研磨轨迹进行绘制，得到传动比为1、2、3、4、5、6六组轨迹曲线，如图2所示。利用MATLAB的M函数文件进行编程。

在工业应用中，调整行星轮系传动比只能通过更改齿轮的方式实现，且行星轮之间的齿轮装配还应满足传动比、邻接、装配和同心四项基本条件[6]。当某个传动齿轮发生故障时，为了保证加工质量，往往需要更换整套齿轮，造价非常昂贵。

1.2 变杆长杆机构运动原理

对常见的曲柄摇杆机构(如图3)运动副进行变形，将连杆与连架杆之间的转动副变化成移动副，这样可以使整体的自由度数量增加1。得到四个转动副与一个移动副的RRPRR型双驱动变杆长五杆机构模型，如图4所示。

在杆机构系统中，当系统确定的运动充要条件为：外界驱动的输入数目等于系统的自由度数目。

在对研磨的轨迹进行运动分析时，我们首先建立三个坐标系：以A点为原点建立的全局坐标系XOY和以C点为坐标原点建立的局部坐标系X1CY1以及以研磨盘回转中心为坐标原点的坐标系。假定上研磨盘相对研磨头F点不发生相对转动，对工作坐标系即以C为坐标原点的研磨头F的运动进行分析，如图5所示。

在X1CY1坐标系中，矢量方程为：

设CF的长度为L，将其向X1轴和Y1进行投影，可以得到：

Lsin(θ0+θ2)=acosθ2+Hsinθ2

yLcos(θ0+θ2)=asinθ2+Hcosθ2

xF=acos(π+θ2)+Hsinθ2

yF=asin(π+θ2)+Hcosθ2

其中，θ0=arctan(aH)

在以A为坐标原点建立的全局坐标系中，对C点的运动方程进行分析，如图6。

B点的运动方程为：

xB=L1cosθ1

yB=L1sinθ1

图2 不同传动比下研磨轨迹Figure 2 Grinding tracks at different drive ratio

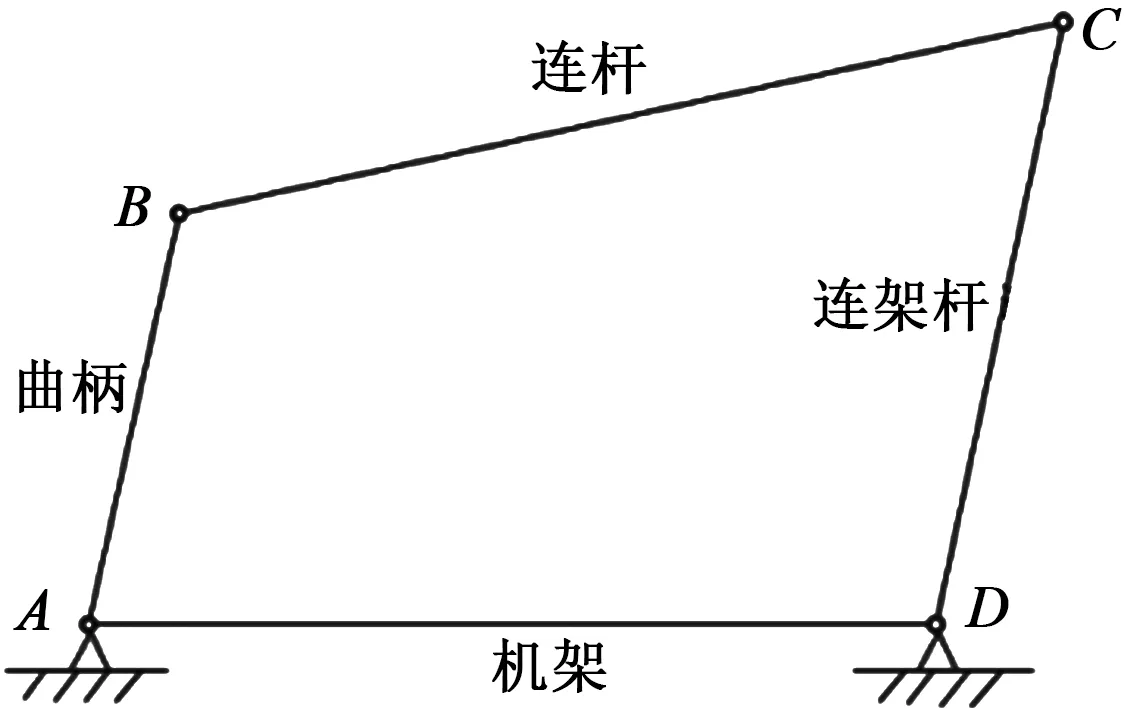
图3 常见曲柄摇杆机构运动简图Figure 3 Motion of general crank and rocker mechanism

图4 变杆长杆机构运动简图
Figure 4 Motion of rod mechanism with variable rod length

图5 以C为坐标原点建立的坐标系Figure 5 Coordinates established from C zero

θ1=ω1t θ2=ω2t图6 以A点作为坐标原点建立的坐标系Figure 6 Coordinates established from A zero

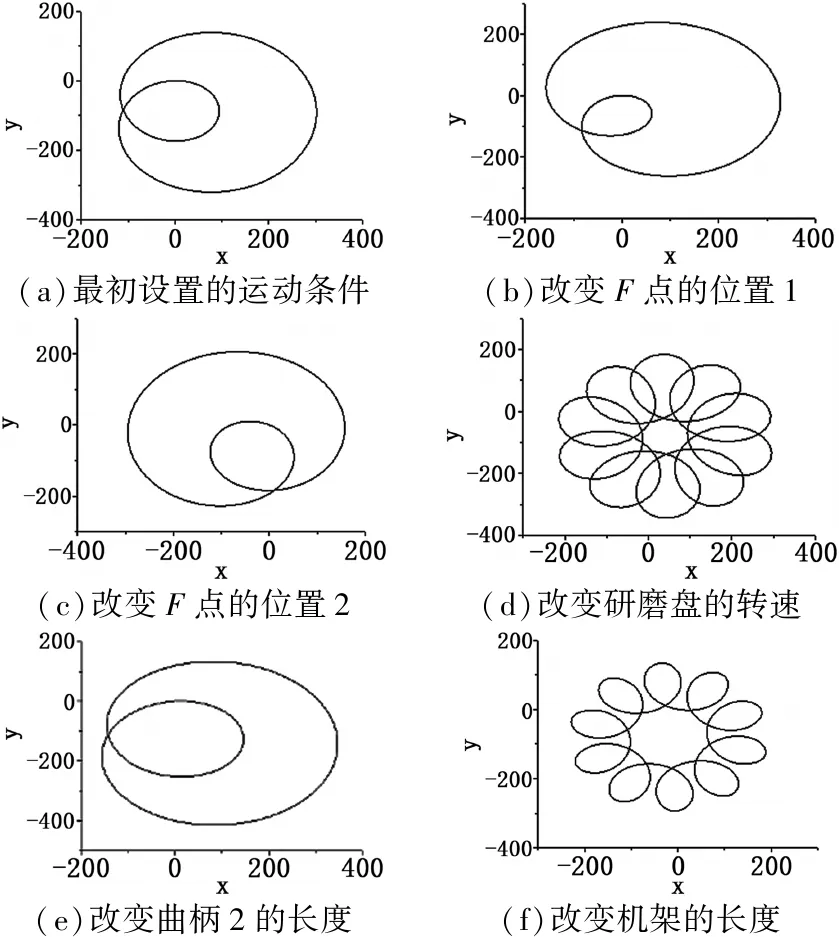
(a)最初设置的运动条件(b)改变F点的位置1(c)改变F点的位置2(d)改变研磨盘的转速(e)改变曲柄2的长度(f)改变机架的长度

图8 不同条件下F点的运动轨迹
Figure 8 Motion tracks ofFat different conditions

C点的运动方程为：

xC=L0+L2cosθ3

yC=L2sinθ3

式中，θ1为曲柄1与机架之间的夹角；θ2为任意时刻连杆与机架之间的夹角；θ3为任意时刻曲柄2与机架之间的夹角；θ0为过F点向滑块做垂线，垂线与CF连线之间的夹角；L1为曲柄1的长度；L2为曲柄2的长度。

应用齐次坐标变换理论，研磨头在全局坐标系XOY中的运动方程的矩阵表达形式为：

化简后得到：

应用齐次坐标变换理论，将研磨头F的运动转移到研磨盘中心位置下，得到运动矩阵方程：

化简后得到：

式中，ωp为研磨盘的转动角速度。

此即为研磨头F点相对研磨盘的运动轨迹方程。

2 ADAMS建模并仿真

建立双驱动杆机构模型并添加合适的驱动与约束，如图7所示。

设置曲柄1的长度为140 mm，曲柄2的长度为145.60 mm，机架的长度230 mm，设定曲柄1和曲柄2的角速度均为10 rads，研磨盘的转速10 rads，在设置这些参数的前提下，运用ADAMS进行仿真，得到F点的轨迹曲线，如图8(a)所示。保持其他运动条件不变，改变F点相对滑块的位置1，得到运动的仿真结果如图8(b)所示；保持其他的运动条件不变，改变F点相对滑块的位置2，得到运动的仿真结果如图8(c)所示；固定其他参数不变，改变研磨盘的转速为-9 rads，得到仿真的结果如图8(d)所示；改变曲柄2的长度为190 mm，固定其他运动参数，得到研磨头F点的轨迹如图8(e)所示；改变机架的长度为270 mm，固定其他运动参数，得到研磨头F点的轨迹如图8(f)所示。

3 结论

(1)双驱动变杆长杆机构实际得到的曲线应该是上面仿真曲线绕研磨盘中心旋转得到的一组复杂曲线。

(2)与行星齿轮机构研磨机相比，双驱动杆机构研磨机在研磨的均匀性和研磨效果上更好。

(3)两曲柄长度的匹配，会影响滑块的摆动范围，使研磨区域发生变化；改变机架长度，同时保持研磨盘位置不动，即给研磨头合适的偏心距，会增加研磨的复杂性，有助于提高研磨的效果；通过调整曲柄回转速度和研磨盘的回转速度，也会增加研磨的复杂性，对于提高研磨效果非常有效。

(4)相比于行星齿轮机构的研磨机，在实现相同研磨效果的前提下，双驱动变杆长研磨机在参数设定上更加方便，更加灵活，实用性更强。