城市轨道交通列车交路开行方案优化研究
张星宇,肖为周,秦菲菲
(苏州大学 轨道交通学院,江苏 苏州 215131)
0 引言
随着城市人口不断增长,部分城市轨道交通线路客流在各区间存在时空分布不均衡特性,基于此背景,单一交路运营组织在高峰期可能会形成部分区段运能供给不足,部分区间运能虚糜、服务水平较低的现象。对此,上海在我国率先实行大小交路模式,截至2018年上海轨道交通线路中已有9条采用多交路运营组织方法[1-3],随后其他城市相继开始探索复杂交路运营模式[4-6]。城市轨道交通大小交路开行方案在固定编组方案和停站方案的情况下,基于大小交路模式,确定各时间段内的列车开行对数,一方面可促进客流与运能匹配,另一方面可节省列车资源,在列车保持合理负荷的情况下提高服务水平和乘客满意度。
国外学者较早研究区域运营管理模式(Zonal Operation),该运营模式使用区间车和全程车两种车型,为城市轨道交通大小交路运营模式奠定了基础。Furth[7]以波士顿某条交通走廊为对象,采用动态规划法确定了区域运行的起终点和发车频率。Canca等[8]以马德里某条通勤线路为例,研究了客流突增情况下以小交路分担客流最大为目标的开行方案问题。另一部分学者的研究集中在区间车的实时控制策略。如Site等[9]提出的公交区间车优化调度模型,计算得出分时段适用不同公交车型的最优发车频率。Tirachini等[10]考虑了票价影响,研究不同发车频率的开行折返区间车公交运营优化模型。通过改变上下行客流OD(Origin-Destination)分布,得出客流较大的车站不宜作为小交路折返站的结果。
国内学者结合各城市运营实践,集中研究了轨道交通多交路运营组织方案。田晟等[11]以乘客出行时间价值和平均载客率最优为目标,以广州地铁6号线为例,采用粒子群算法得出最优地铁行车组织方案。王申[12]、白广争等[13]以投入运用车组数最少为目标建立列车均衡开行方案优化模型,以成都地铁2号线为例进行测算。王媛媛等[14]考虑了乘客在途时间和车底配置费用,利用Lingo软件求解建立多目标模型,通过算例验证了模型的合理性。许得杰等[15]考虑乘客等待时间为乘客利益,车辆走行公里和列车运行时间表示为企业成本,构建多交路和变编组的优化模型,并设计受控随机搜索算法求解。王彦栋[16]考虑线路断面客流量和车底使用数,采用模糊数学方法计算载客量之差,求解多目标规划模型后得出最优方案。
综上所述,本文结合城市轨道交通运营组织特点,在已知OD客流分布及相关运营参数的情况下,建立模型求解得出最优开行方案,使乘客出行成本和运输企业运营成本达到最小,以期方便乘客的同时保证城市轨道交通良好的服务水平。
1 问题描述
1.1 模型基本假设
1.1.1 交路模式描述
研究对象为具有n个车站的城市轨道交通直线型线路,S={Sj|j=1,2,...,n}为车站集合,列车交路如图1所示。为便于运营组织线路采用两层交路,其中大交路列车全线贯通运营,列车从车站S1行至车站Sn后折返,小交路列车为部分区段运营,车站Sa及车站Sb为折返站;小交路列车发车频率为大交路列车发车频率的整数m倍,列车定员为Cz,大小交路列车共线运行区段记为M2,其他区段记为M1。
1.1.2 基本假设
(1)从规划设计的角度考虑,线路中每个车站均具备折返条件。
(2)研究时段内,大小交路列车发车间隔不变,上下行列车成对开行。
(3)研究时段内的客流量由这一时段内的列车平均分担。
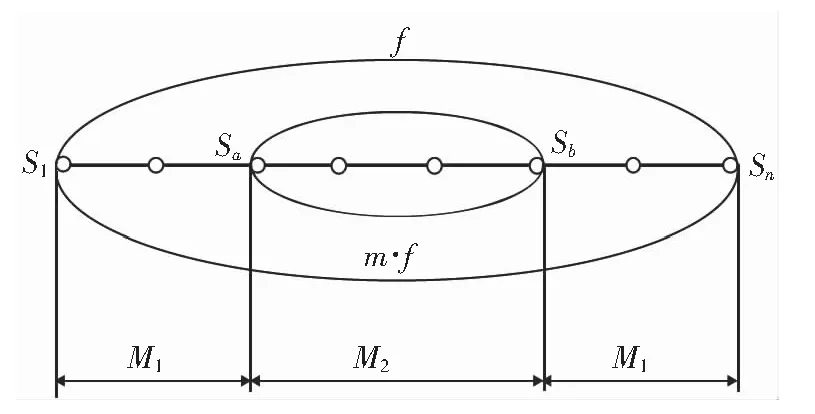
图1 大小交路模式示意图Fig.1 The illustration of full-length and short-turn routing long & short routing mode
(4)为便于绘制运行图,小交路列车发车频率为大交路列车发车频率的整数倍。
(5)列车车底周转方式为大小交路独立运营使用,且具有相同的车型和编组。
(6)列车停站方案为站站停,停站时间由站内上车乘客数量决定。
1.2 参数及变量定义
列车从S1站出发至Sn站方向为上行方向,反之为下行方向;本文用i、j标记车站,用q(i,j)表示研究时段内从i站前往j站的乘客数;t(i,j)表示从i站到j站的区间运行时间。
研究时段T内,大交路列车开行对数记为f,小交路列车开行对数为大交路的m倍,记为m·f。客流分为M1区段大交路OD客流Q1和M2区段小交路OD客流Q2两部分,根据假设(3),其中Q1仅被大交路列车分担,而Q2可被大小交路列车共同分担,分担率为θ=1/(1+m)和1-θ。
2 建立模型
城市轨道交通线路具有较强的固定性,列车运行只能沿固定轨迹运行,供给难以匹配。运输企业希望降低运营成本,节约资源,改善安全性;乘客希望出行能够安全高效,改善舒适性。因此基于大小交路模式的列车开行方案应以乘客出行成本和企业运营成本最小为目标。
2.1 乘客出行成本
乘客出行成本包括乘客等待时间和乘客乘车时间,其中乘客乘车时间主要是全线乘客乘坐列车包含的区间运行时间;乘客等待时间即为乘客在列车站台候车的时间,统计数据表明,当行车间隔较小时,单位乘客的平均等待时间趋近于行车间隔的一半。因此M1区段乘客平均等待时间t1w可表示为T/(2·f),M2区段乘客平均等待时间t2w为T/[2·f·(1+m)],对应客流可表示为:
(1)
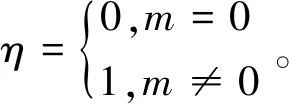
(2)
(3)
令Tw为全线乘客总等待时间,min;Tv为全线乘客所花费列车区间运行时间,min。
Tw=Q1·t1w+Q2·t2w。
(4)
(5)
于是乘客出行成本最小化目标(Z1)可表示为两部分之和:
2.2 企业运营成本
企业运营成本主要包括固定成本、运营可变成本和停站成本。其中,固定成本主要受车底配置数量影响;运营可变成本即列车运行成本,主要取决于车辆走行里程;停站成本取决于列车停站次数。企业运营成本最小化目标可表示为:
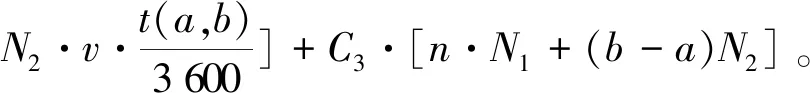
(7)
式中:N1、N2分别表示大小交路车底运用数量,列;v为列车平均运行速度,km/h;C1为单位车底配置费用,元/列;C2为单位列车运营成本系数,元/(列·km);C3为单位停站成本,元/次。
根据假设(6),本文列车停站时间由站内上车乘客数量决定,列车周转时间为列车区间运行时间、停站时间和折返时间之和。即
(8)
(9)
于是大交路列车运用数可表示为:

(10)
同理小交路列车运用数可表示为:
(11)
式中:T1,周、T2,周分别为大小交路的列车周转时间,s;σ为单位乘客平均上车时间,s;t折、t中折为列车在折返站和中间站的折返时间;t远为列车各区间的远行时间;t停为列车在各站的停站时间;「⎤表示向上取整。
2.3 约束条件
根据基本运营组织条件及客流需求,基于大小交路模式的列车开行方案需要满足:
N1+N2≤N0。
(12)
(13)
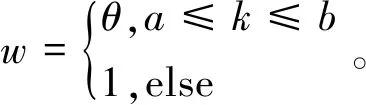
(14)
(15)
f+m·f≤T/I追。
(16)
f≤T/t折。
(17)
m·f≤T/t折。
(18)
f≥fmin。
(19)
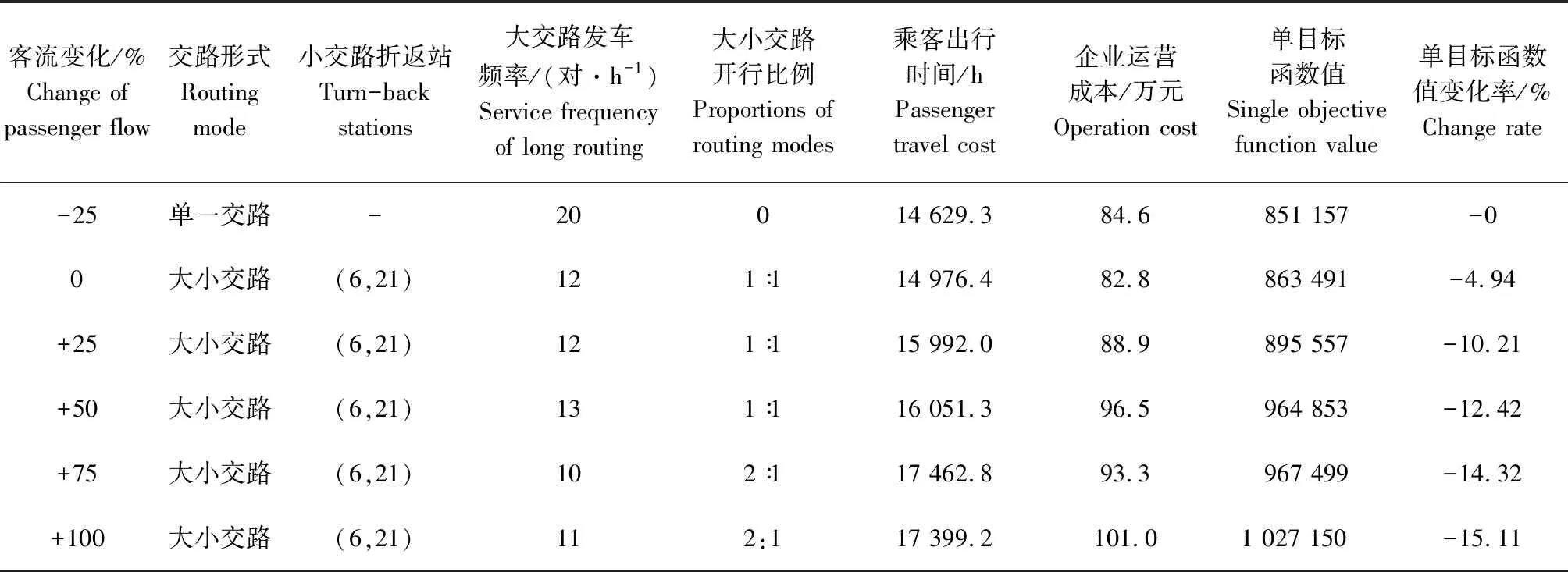
f∈N+,m∈N,1≤a (20) 式中:N0为单一交路列车运用数量;α为列车最大断面满载率;Cz为列车定员;I追为最小追踪间隔时间;fmin表示最小发车频率。 公式(12)为车底配置数量约束;公式(13)至公式(16)为最大满载率约束;公式(16)保证满足最小追踪间隔约束;公式(17)和公式(18)保证线路通过能力满足折返能力约束;公式(19)满足最小发车频率约束;公式(20)保证大小交路发车频率为整数和限制车站编号的取值范围。 本文所建模型的决策变量为大小交路列车发车频率f、小交路列车折返站(Sa,Sb)及大小交路列车开行比例m。由于模型为双目标非线性混合整数规划模型,拟将双目标化为单目标后求解,主要分为两个步骤。 (1)通过线性加权法将双目标问题转化为单目标问题。 (2)应用遗传算法求解单目标优化问题。 本文采用线性加权法将乘客出行时间、企业运营成本的双目标转化为单目标,表示为: minZ=ω1Z1+ω2Z2。 (21) 遗传算法是模拟生物在自然环境中的遗传和演化过程而形成的一种自适应全局优化概率搜索算法,适用于处理传统搜索方法难以解决的非线性优化问题,可广泛应用于轨道交通规划设计和开行方案组合优化问题,这里遗传算法的流程[17-18]不再赘述。 以某市轨道交通直径线为例,选取未来年工作日早高峰时段(8:00-9:00)客流预测数据,断面客流如图2 所示,线路区间运行时间和模型参数取值分别见表1和表2。 图2 区间断面客流图Fig.2 Section passenger volume 表1 线路区间运行时间 表2 模型参数取值Tab.2 Parameter values used in case study 4.2.1 最优开行方案 对案例进行求解,得到最优列车交路方案见表3,即采用大小交路套跑形式,全线贯通发车频率为12对/h的大交路,在车站6和车站21之间开行小交路,大小交路最优开行比例为1∶1,在此方案下,线性加权单目标函数值达到最小。 求解最优列车交路方案与现状采用的单一交路方案相对比,其效果评价指标见表4。由表4可以看出,与单一交路模式相比,乘客出行时间会有所增加,而企业运营成本会大幅减少。在线性加权总成本单目标函数值降低4.94%的情况下,运用列车数从58列降到53列,节省5列车可转为备用,列车走行里程降低18.70%,最大断面满载率降低3.30%,满载率均衡性指标上行降低19.85%,下行降低4.95%,上下行断面满载率更为均衡,运输效率提高22.37%,得到大幅提升。可见,在一定条件下,运输企业可以考虑采用大小交路运营模式,可以减少企业运营成本,提升服务质量,但相应地会以增加乘客出行成本为代价。 表3 最优列车交路方案 表4 列车开行方案效果指标对比Tab.4 Effect comparisons between different train plans 4.2.2 灵敏度分析 (1)小交路折返站位置 由表5可知,固定其他参数,当小交路折返站位置靠近首末站,即小交路区段长度增长时,发车频率有减小的趋势,同时乘客时间成本会减少,但企业运营成本却会增加;当小交路区段长度缩短时,乘客时间成本会增加,总成本降低速率变缓,总体来看小交路区段长度既不宜过长也不宜过短。因此在实际运营中,为使乘客和企业供给双方利益最大,应该根据客流特征及线路的实际情况科学合理的设置小交路折返站。 (2)小交路区段客流比重 由表6可知,将小交路区段客流量较原客流量分别变化-25%、+25%、+50%、+75%、+100%,固定其他参数,当客流比重增加,小交路折返位置保持不变,即客流分布不均衡的情况下,列车发车频率逐渐增大,大小交路开行比例相应变化,单目标函数值降低变化率则呈现增加趋势,而当客流量减小到一定程度时,最优交路方案退化为单一交路方案。说明是否开行大小交路取决于客流特征条件,小交路区段客流比重越大,越适合开行大小交路。 表5 小交路折返站对列车最优交路方案的影响Tab.5 Effect of turn-back stations on optimal train route schemes 注:加粗内容表示最优开行方案。 Note: The bold content indicates the optimal train plan. 表6 小交路区段客流比重对列车最优交路方案的影响Tab.6 Effect of passenger flow proportion on optimal train plans in short-turn routing section 根据线路客流分布不均衡特性,为使客流与运能更好的匹配,采用大小交路运营组织形式,考虑客流需求和线路能力等约束,建立了城市轨道交通列车交路开行方案优化模型,使用线性加权法将双目标模型化成单目标模型后采用遗传算法进行求解,通过案例分析对比单一交路运营效果,并对小交路折返点和区段客流比重进行灵敏度分析,得出了以下结论。 (1)一定客流条件下,大小交路运营模式可以降低运输企业运营成本,减少运用列车数量,提高断面满载率均衡性,有效提高运营效果,但这会以增大部分乘客的出行成本为代价。应对客流高峰期,可以压缩行车间隔,当运用列车数紧缺时,大小交路是相对较优的运营组织形式。 (2)大小交路模式小交路区段不宜过短,乘客等待时间会增加,频繁折返会增加运营组织难度,也不宜过长,此时运营成本降低幅度不大,不能突显大小交路模式优势;小交路区段客流所占比例越大,采用大小交路运营组织的总成本节省越多。当线路断面客流曲线较为陡峭,客流分布不均衡性较大时,建议运输企业采用大小交路模式,适当延长小交路运行区段,根据实际进行调整。3 模型求解
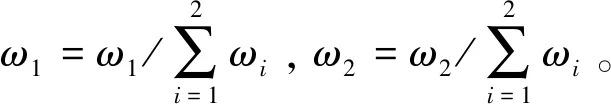
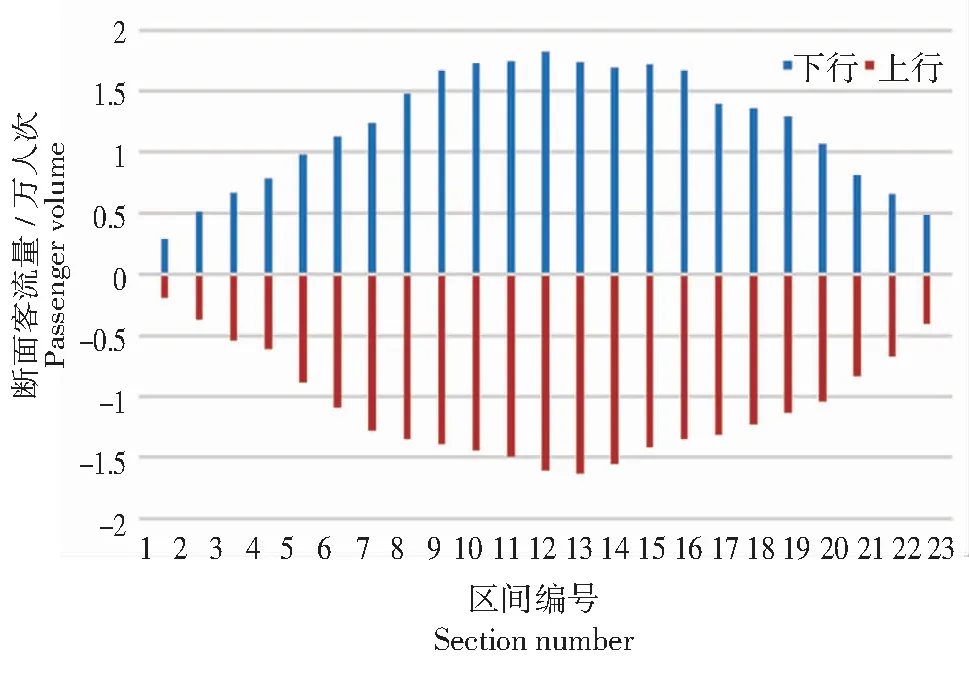
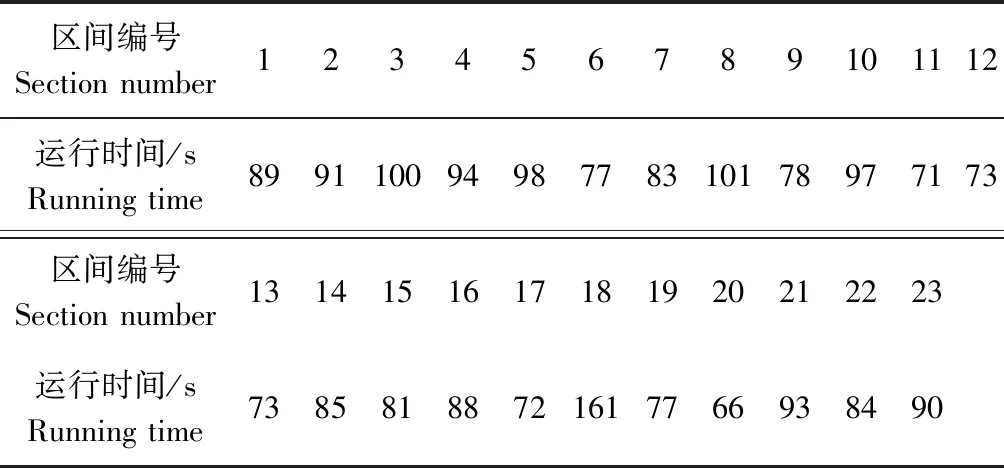
4 案例分析
4.1 案例及模型参数

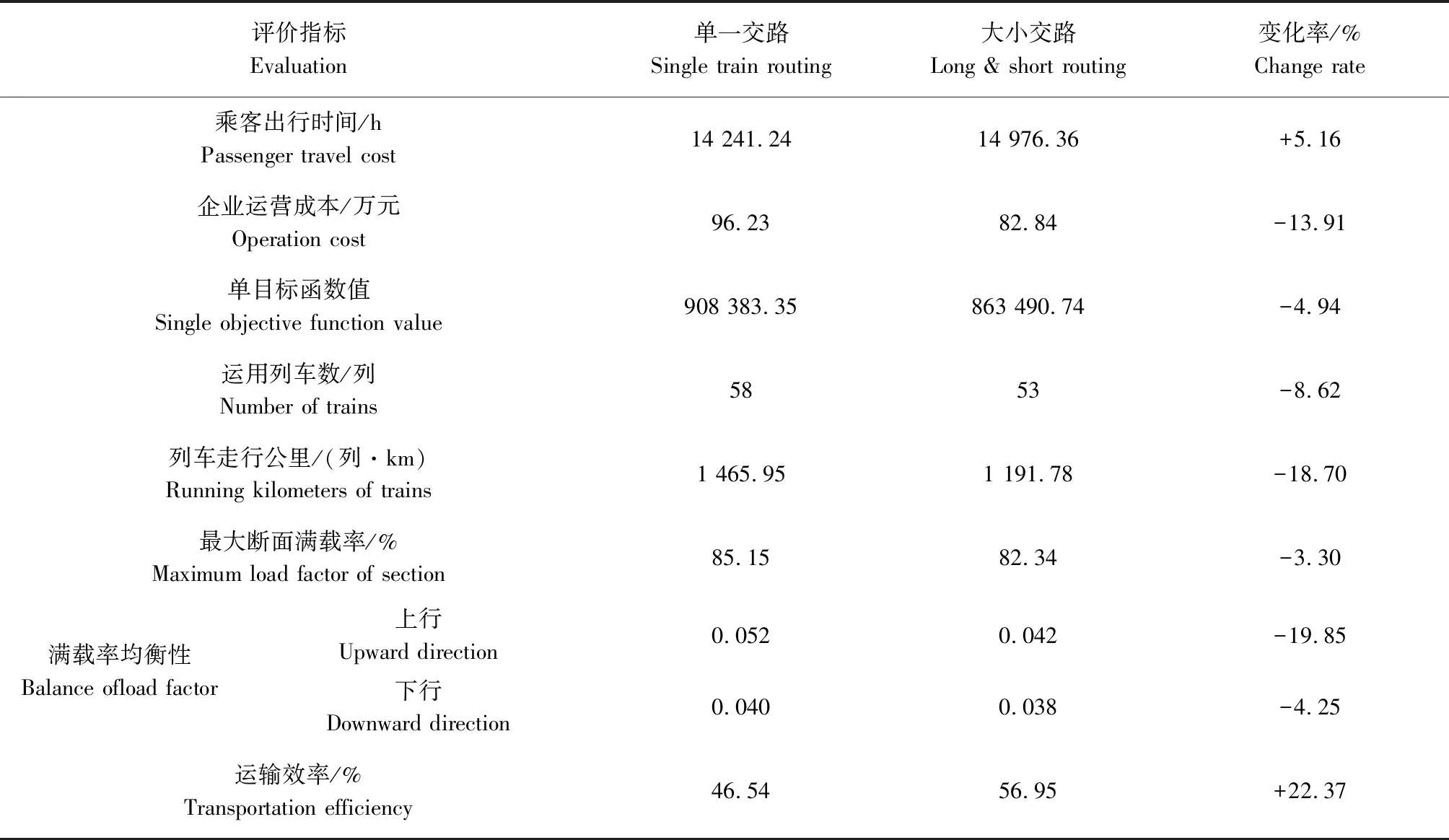
4.2 结果分析


5 结束语

