一种非线性路径跟踪方法的应用

刘来华

（中国船船重工集团有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

无人驾驶载具作为一种具有自主操作能力、机动灵活、行动隐蔽、无人员伤亡等特点的智能化平台，部署机动、使用方便，可以在危险区域或者不适宜有人操作的区域独立自主执行任务，具有良好的费效比和广泛的应用前景。

无人驾驶载具主要包括：地面无人智能车辆、水面无人艇、空中无人机、水下机器人。其自主航行能力作为衡量装备智能化程度高低的核心技术之一，直接影响装备的价值，也受到越来越广泛的重视。

路径跟踪是实现无人驾驶载具自主航行的关键技术之一，也是无人驾驶载具必须具备的基本功能之一。但是在复杂环境下的各种扰动给无人驾驶载具的路径跟踪控制精度带来了难度和挑战，其结果直接影响系统的智能化作业效果。

目前，国内外学者都对路径跟踪方法进行了深入的研究，形成的文献主要分为 4类：世界常用算法介绍[1-3]、基于数学模型的控制仿真算法研究[4-6]、半实物仿真控制算法研究[7-9]、基于实物平台的控制算法介绍说明[10-11]。本文的算法属于第4类。

本文介绍了一种新型的非线性路径跟踪算法。该算法结合传统的PID算法，不依赖数学模型、易于实现。经过计算机控制仿真试验和实物样机试验验试，通过对比发现：相对于传统的线性PID控制方法，本文算法在控制精度、适应环境强扰动性等方面有显著优势，具有一定的市场应用价值。

1 常用线性制导控制算法

在路径跟踪技术中一般采用2种方法：直接法和间接法。

间接法是将无人驾驶载具的制导与控制问题分开为外环的制导回路和内环的控制回路。外环制导回路通常使用基于几何学和运动学特性的策略产生期望加速度。内环控制跟随外环产生的加速度指令，输出转向角度指令。通过双环控制实现路径跟踪。

直接法是使用集成策略，内环和外环被集成设计为一体。可以应用一些现代控制和设计技术，依据数学模型和算法，根据输入的航迹偏差直接产生控制舵机角度或转向角度的输出指令，实现路径跟踪。

在实际应用中，将内环和外环分开的方法更加常用。这种方法对于无人驾驶载具的内环控制更简单且易于建立。在算法测试时，可以将内外环分开进行独立的调试测试，调试简单方便。图1为常用经典内外环分开的双环线性路径跟踪算法控制原理图。

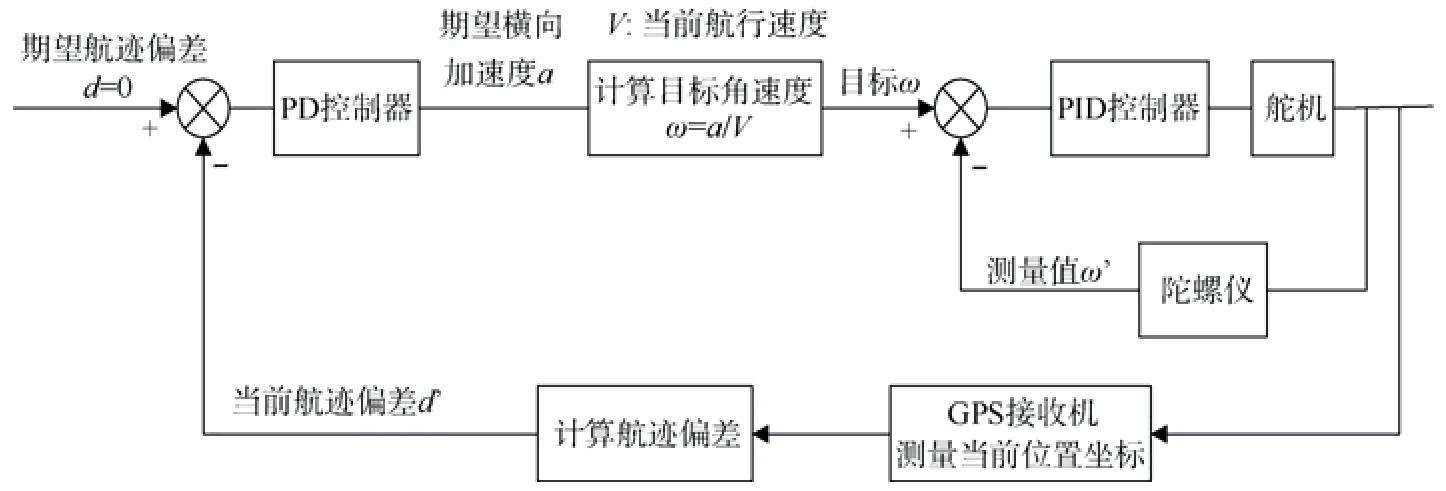
图1 常用路径跟踪控制器Fig.1 Normal path tracking controller

线性控制器广泛应用在无人驾驶算法的外环制导。通常情况下比例微分（PD）控制器用于控制航迹误差，在环境无扰动且当目标路径为直线时，这种简单的策略可以提供很好的外环控制性能，具有较好的直线路径跟踪能力。

无人艇在实际航行过程中，高海况扰动会实时引起航速和航向的变化。同样，无人机在飞行过程中也会受到气流、风向的扰动而影响航速和航向。传统的线性 PID控制算法在外环中包含航迹偏差及航迹偏差的变化率，但未考虑扰动带来的航速大小和方向的实时改变。所以，从理论上就决定了其在高海况下或强对流天气下的抗扰能力不强、控制精度不高。同时，当无人驾驶载具在需要对复杂的曲线或者圆形路径进行紧密跟踪时，传统PID算法中航迹误差的线性反馈无法提供满意的性能。

2 新型非线性路径跟踪算法

在无人驾驶技术的路径跟踪方法方面，可参考导弹制导方法。

在导弹制导领域主要有视线导航法（1ine of sight，LOS）、纯跟踪制导法（pure pursuit guidance，PP）、平行接近制导法（constant beating guidance，CB）3种方法。视距导航LOS方法应用于地对空制导，PP方法应用于空对地制导，CB应用于空对空制导。其中，LOS方法以其良好的性能及控制效果在无人驾驶载具的路径跟踪领域得到了广泛的应用。

本文所述的非线性路径跟踪算法采用 LOS方法，在路径跟踪控制算法的外环采用一种非线性算法计算产生横向加速度，以取代传统的线性PD控制器，内环控制器与传统方法相同。此非线性制导率称之为L1控制算法。

视线导航的控制方法（LOS）原理：通过在目标路径上选取合适的参考导航点，引导无人驾驶载具跟踪选取的参考导航点，使无人驾驶载具能够逐渐接近目标路径并最终沿着目标路径前行，达到路径跟踪的目标。

LOS制导算法独立于无人驾驶载具的数学模型，具有参数整定容易、计算开销较小、稳定性较高、收敛性能较好和易于工程实现等特点，因而被广泛应用于各类无人驾驶载具的路径跟踪控制算法研究中。

2.1 非线性L1算法原理

在目标路径上选择1个参考点，在每一个时间点定义1个圆周路径。这个圆过参考点和无人驾驶载具的当前位置，且与航行速度相切，通过参考点产生一个横向加速度指令as。无人驾驶载具的速度为V，转向半径为R，参考点的位置在目标路径上，并与无人驾驶载具距离L1，L1可由用户设定调节。

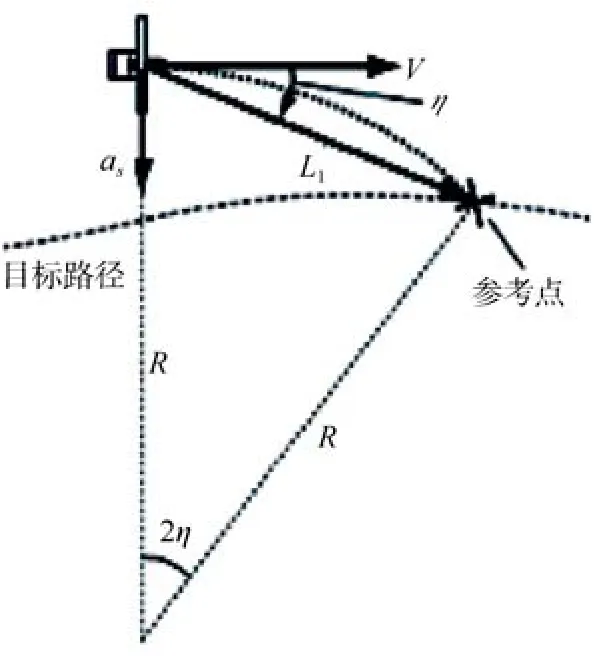
图2 运动几何学原理图Fig.2 Principle diagram of kinematic geometry

根据运动学和几何学，可以得出：横向加速度

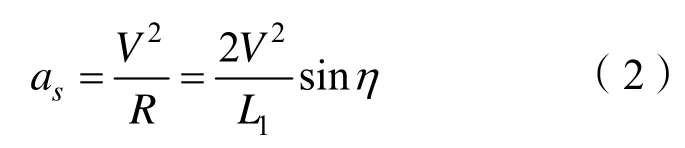
速度 V可由传感器实时测量获得，L1由用户预先设定，即速度V和L1均为已知量。根据上述公式，只需要得出转向角η值就可求出外环横向加速度值as，随后进行内环（角速率）的闭环控制，从而最终实现直线或曲线路径跟踪的目标。

2.2 求解转向角

以直线跟踪为例，转向角η由2部分组成，即η=η1+η2，根据几何学有：

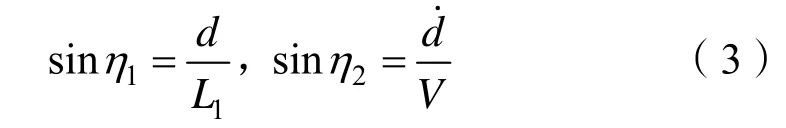
即：

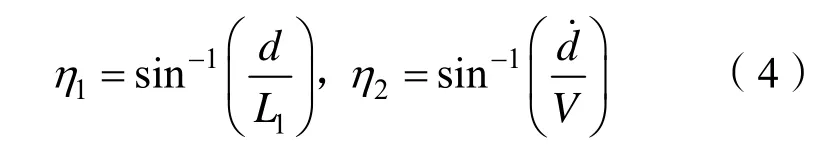
在求出η1和η2后，即可得出转向角η的值。

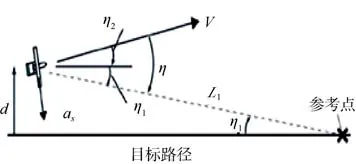
图3 直线跟踪几何关系图Fig.3 Geometrical relation diagram of line path tracking

2.3 线性化处理

假设η角很小，则η1、η2也很小，根据几何学：

因此，L1非线性算法进行线性化处理之后等价于1个PD控制器来控制航迹误差，与传统的线性控制算法完全相同。

在转向角很小的情况下，两者的控制效果和精度完全相同，即L1控制算法完全兼容传统线性PD控制算法。

在转向角较大的情况下，不适宜做线性化处理，两者的控制效果和精度不同。

2.4 稳定性分析

本文以直线路径跟踪情况为例进行非线性李雅普诺夫稳定性分析。

系统模型被表示为下面的运动学公式：

制导率为

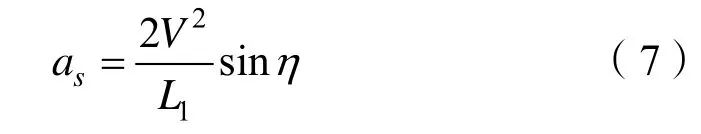
为了参考点有唯一存在性，假设：

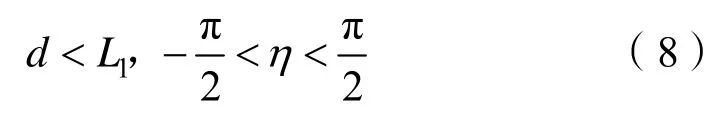
则李雅普诺夫函数为

由模型图有：

则式（9）变为

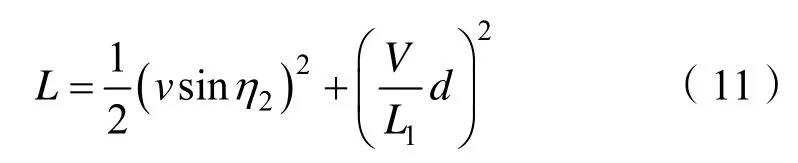
这是一个正定函数，对式（9）进行时间求导可得出：

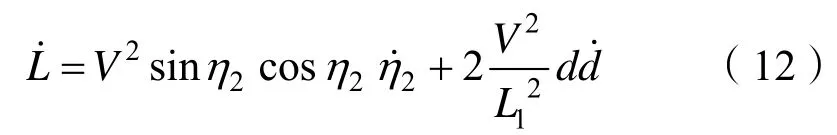
使用公式（6）和公式（10），有：

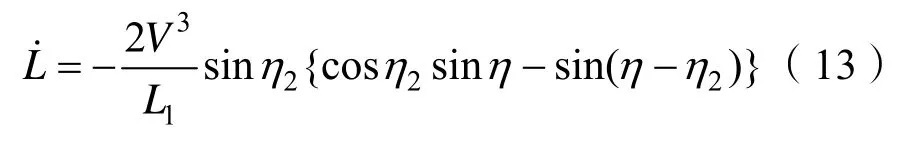
最后由：

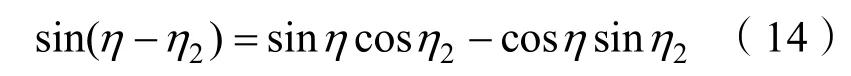
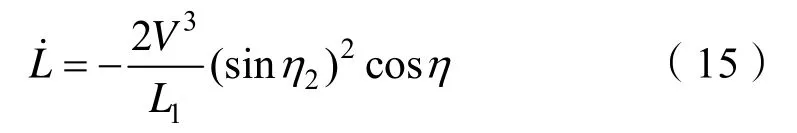
因为|η|＜π/2，所以L˙是半负定的。故应用不变集理论，由L=0得到的解就只有d=0、η2=0。因此L1算法对于 d ＜L1、|η|＜π/2的情况是渐进稳定的。

2.5 L1算法工程化处理

根据稳定性分析结果：L1算法对于 d ＜L1、|η|＜π/2的情况是渐进稳定的。在实际工程应用中经常会遇到 d ＞L1、|η|＞π/2的情况，需要进行工程化处理，以确保算法的控制结果保持收敛。

在|η|＞ π /2即转向角大于 90°度时，可在软件设计中对η进行限幅，使其满足|η|＜π/2，即限制每次的转向角不超过π/2。

在 d＞L1即距离目标路径很远时，可以将目标路径跟踪问题转变为航点跟踪问题，即跟踪目标路径中的起始航点。

航点跟踪原理：无人驾驶载具与起始航点的位置已知，可以得出其航向A，速度的方向B可以由罗经或惯导设备获取。获得A和B值，则可求出转向角η的值，随后转变为传统的动态航向保持问题，最终达到跟踪目标航点的目标。

3 L1路径跟踪算法仿真测试

选择小型固定翼飞行器为仿真目标对象，进行空气动力学建模。通过控制仿真的方法来对比在不同目标路径和风速扰动条件下非线性L1算法与线性PID算法的性能差异。

非线性L1算法同样适用于圆形路径跟踪。在圆形路径上选择参考导航点，航迹偏差为飞行器当前位置距圆心的距离与圆形直径值的差值，采用的LOS原理及运动几何学与直线路径跟踪完全相同。

3.1 直线路径跟踪的仿真效果对比

设定初始条件：巡航速度为25 m/s，L1=150 m，航迹偏差d=10 m。起始时无人飞行器的航向平行于直线路径的方向，进行两种控制算法的仿真试验。

仿真结果表明：在起始转向角很小的情况下，2种算法对于跟踪直线路径的性能和效果几乎完全一样。同时，也印证了本文2.3章节中的理论分析结论。

3.2 无风条件下圆形路径跟踪仿真

根据数学模型进行控制仿真，结果表明：使用PD控制器的稳态误差约为40 m。稳态误差的出现是因为航迹误差的位置参考命令是抛物线形式的，而目标路径为圆形。采用PID控制器后，积分器消除了稳态误差，但在初始阶段的误差仍然存在。L1法对曲线路径的跟踪效果很好，在初始阶段与目标曲线的偏差不超过5 m。

3.3 有风条件下曲线跟踪仿真

有风条件下仿真结果表明：在东向风力为5 m/s情况下，对于 PD控制器，在初始阶段后，航迹误差范围为30～60 m；对于PID控制器，航迹误差范围为-20～20 m。

当飞行器在顺风区飞行时处于圆形路径外，而在逆风区时则处于圆形路径内。因为在顺风区时，飞行器相对于惯性坐标系的速度增加。如果要保持对路径的精确跟踪，飞行器必须产生一个大的加速度指令。而增益不变的线性控制器的固有局限使其并不能立刻纠正这个误差，导致航迹误差偏大。

4 飞行器样机测试

4.1 飞行器样机参数

飞行器选用固定翼飞机，翼展长度2.5 m，重量约10 kg。在巡航速度为25 m/s，L1=150 m的设置条件下，对圆形路径跟踪进行测试，圆形路径的半径为250 m。

4.2 飞行器路径跟踪效果

在飞行器沿圆形路径飞行时，航迹和目标路径的横向偏差 75%的时间保持在±2 m，而 96%的时间保持在±3 m。

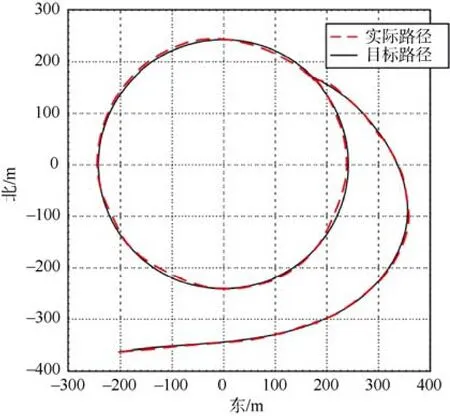
图4 飞行器跟踪圆形路径的实测结果Fig.4 Test result of flight vehicle traces circular path

测试结果表明：L1算法动态性能好、控制精度高、抗扰能力强，跟踪圆形路径的效果特别好。

5 无人船测试

5.1 抗浪仿真测试

无人船模型选用小型固定双桨的双体船运动模型。先建立波浪干扰下的运动模型，忽略风和流的影响，主要考虑波浪作用，对模型施加各个方向的波浪，对L1算法与传统PID算法进行仿真对比测试。

抗浪仿真结果表明：传统PID算法在随浪和横浪的作用下，路径跟踪偏差随着海浪的增大而加剧变大；L1算法可同时对随浪和横浪进行抑制，减小路径跟踪静差，且随着浪高的增大效果愈明显，具有较好的抗浪能力。

5.2 抗风仿真测试

无人船模型选用大型双体船运动模型。忽略波浪的影响，对模型施加各个方向的风力，对L1算法与传统PID算法进行仿真对比测试。

抗风仿真结果表明：在顺风和横风的作用下，传统PD算法无法准确收敛到目标路径，进而产生跟踪静差，且随着风速增加而加剧；L1算法可同时发挥对顺风和横风的抑制作用，减小路径跟踪静差，提高路径跟踪的精度，明显地提高了抗风干扰能力。

5.3 无人船水库航行测试

试验船采用无人双体船，船长3.5 m，宽2.5 m，采用固定双推进器模式，推进器为电力驱动方式。控制系统通过分别独立调节左右 2个推进器的转速实现调速和转向的目标。

双体船的路径跟踪算法采用本文的非线性控制算法，设定巡航速度为 4 m/s、目标路径包含 2段直线和1段曲线，曲线两端分别连接2段直线。

在水库水面有风浪流综合影响的天气下，实地进行无人船路径跟踪试验，实时测量航迹并与目标路径进行对比，测试本文算法的路径跟踪效果及抗扰动性能。

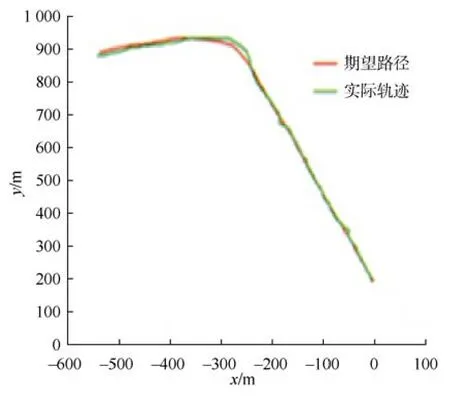
图5 双体船路径跟踪测试Fig.5 Path tracking test of catamaran

测试结果表明：L1非线性算法能在存在一定外部扰动的情况下，准确跟踪直线路径和曲线路径，具有较强的环境适应能力。

6 结束语

本文介绍了一种非线性路径跟踪方法，阐述了该方法的运动学原理、稳定性分析、工程应用方法、与传统PID线性算法的关系。

通过与传统PID/PD路径跟踪算法进行全面分析对比，本文算法具有动态性能好、控制精确度高、抗扰能力强的特点。

该算法能稳定跟踪直线路径和曲线路径，不依赖于数学模型、易于实现。适用于中低速无人艇、无人飞行器、无人智能小车的室外路径跟踪应用场景，具有一定的市场应用价值。