一种基于声学回波统计的水下散射体数量密度评估模型

梅新华

（中船重工鹏力（南京）大气海洋信息系统有限公司，江苏 南京 210000）

0 引言

水中悬浮颗粒（如泥沙）、气泡群、鱼群等散射体是海洋工程应用中常见的散射体[1]，对这类散射体的数量密度进行评估不仅具有直接的工程应用价值，并且其作为水声研究中常见的混响散射体，是水下声学应用研究的重要内容[2]。目前对这类散射体群的数量密度评估主要包括光学与声学2类方法，其中声学方法具有由于探测距离远的优点，更为广泛应用前景。

与单一散射体不同，这类散射体的声散射是由多个处于随机运动状态的散射元相干叠加而成，因而其回波信号具有明显的随机性与波动性，这给基于声学方法的水下散射体数量密度评估带来了挑战。根据混响理论研究[3]，水中悬浮颗粒、气泡群、鱼群等混响散射体可用泊松概率模型对其空间分布进行描述。对于泊松混响，根据大数定理，当散射体的数量密度较大时，混响瞬时值分布服从正态分布，对应包络的瞬时幅度服从瑞利分布。但在散射体的数量密度较小的情况下，其回波包络瞬时幅度会偏离瑞利分布，且其偏离瑞利分布的程度与散射体的数量密度有关。因此从回波信号统计的角度出发，通过选取合适的统计特征量和数值关系模型推导，可实现散射体数量密度的评估。本文对散射体群声学回波信号统计特征进行了研究，建立了一种基于声学回波能量统计的水下散射体数量密度评估模型。

1 模型简介

脉冲信号是声呐水下探测中的一种常用信号形式，当声呐发射信号为脉冲信号时，常用散射体回波信号的能量（或强度）用来表征散射体的散射能力。对于体积混响散射体，一般来说散射体的数量密度越大，其回波信号能量的期望值越大。但由于散射体群处于随机运动状态，在某个瞬时测量时刻其回波信号能量是个随机数，因此单纯地从某个瞬间回波信号来评估散射体群是无意义的，也是不现实的。本文拟通过对散射体群回波信号能量的统计特征进行建模，达到评估散射体数量密度的目的。

图1为声学方法测量散射体的示意图，测量过程中散射体中的任意散射元的位置、姿态、数量是随机变化的。本文从以下因素考虑任意t时刻声呐波束照射的某区间内散射体总的回波：1）该时刻区间内散射元的数量；2）由于散射元尺寸大小，相对入射声波的姿态角随机变化而决定各散射元回波信号的幅度；3）该时刻各散射元的位置（回波的声程）。在忽略测量过程中声呐与散射体之间的相对运动和散射体之间的二次散射的情况下，目标区间中随机运动散射体的回波是各散射元回波信号的相干叠加。

基于以上分析考虑，对水中悬浮颗粒（如泥沙）、气泡群、鱼群等散射体回拨信号进行建模。设声呐发射信号为 CW 信号：s (t)=c os(2π f0t)rect(t/ Tp)。式中： f0为信号频率；Tp为信号脉冲宽度；rect(t/ Tp) =u(t)-u ( t- Tp)， u( t)为单位阶跃函数。由于散射元的运动姿态与位置的随机性，其回波的相位是随机的，散射体总的回波是各散射元回波的相干叠加。设t时刻有N个散射元对回波有贡献，其回波可表示为

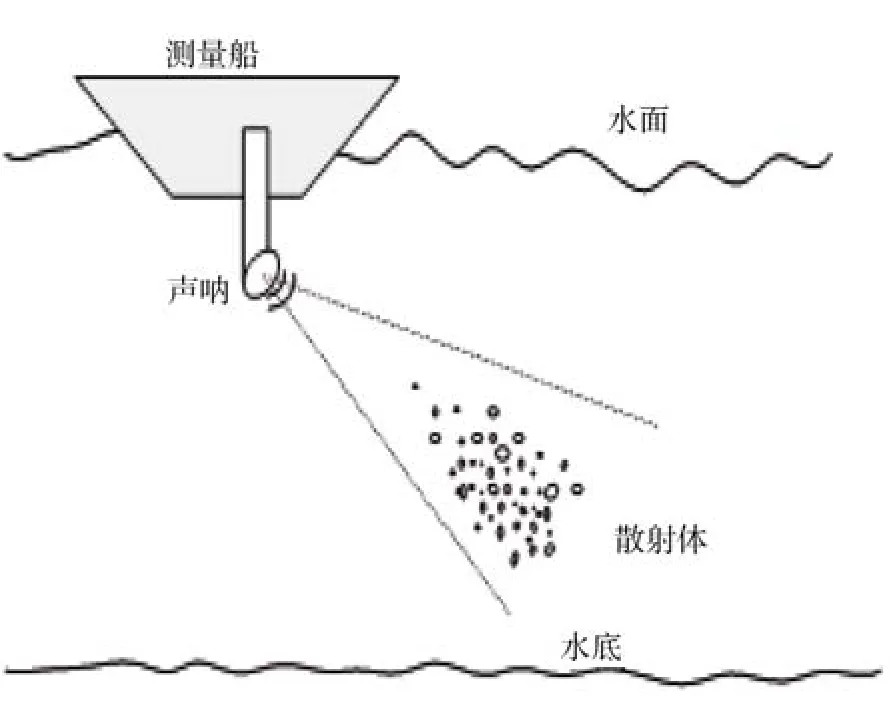
图1 声学测量散射体数量密度示意图Fig.1 Schematic diagram of scaterer number density by acoustic measurement

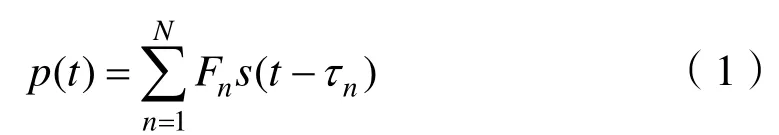
式中：Fn为第n个散射元的回波幅度；τn为其回波声程对应的时延。对应的回波积分能量为

式中：t1、t2对应的测量区间为，c为水下声速。N个散射元任意时刻回波的能量是各散射元单独回波与散射元间回波干涉叠加的结果，其离散形式可表示为[4]

式中：Fm、Fn分别为第m个与第n个散射元的回波幅度；参数Cmn为第m个与第n个散射元回波的相关系数，满足：

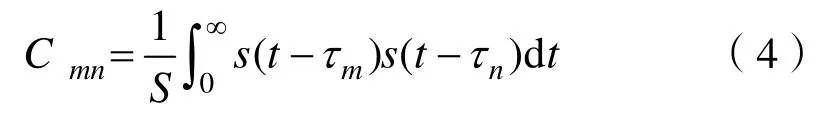
考虑ε的期望，根据回波积分理论，多次测量过程中由于散射元的位置或其回波信号的相位是随机变化的，在忽略散射元的2次及2次以上散射时，散射体群回波的平均能量与散射元的数量成正比。结合式（3），可将ε的期望表示为

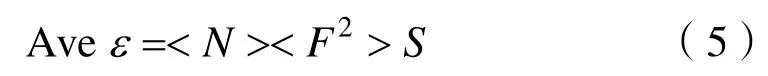
式中：＜N＞为多次测量过程中散射元数量的期望；＜F2＞表示N个散射元回波幅度的二阶矩。

进一步考虑ε的方差：

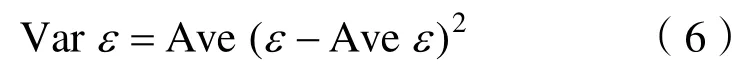
根据文献[4]可以将ε-Ave ε表示为

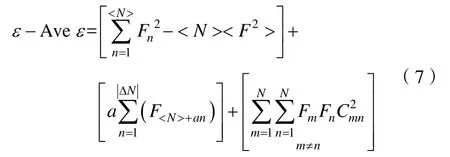
式中：ΔN=N -＜N＞，a为符号函数，由

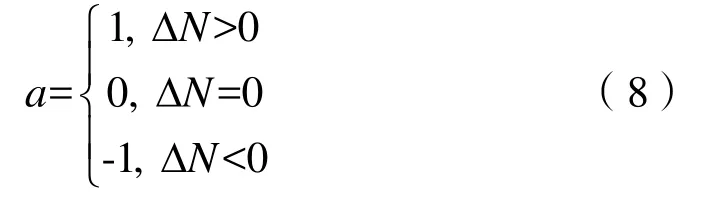
可以看出式（7）右边的第1项仅与散射元回波幅度的波动有关，第2项仅与测量区间中散射元数量的波动有关，第3项则仅与散射元回波在测量区间中的相关性有关，容易理解三者互不相关。此时积分能量ε的方差满足：

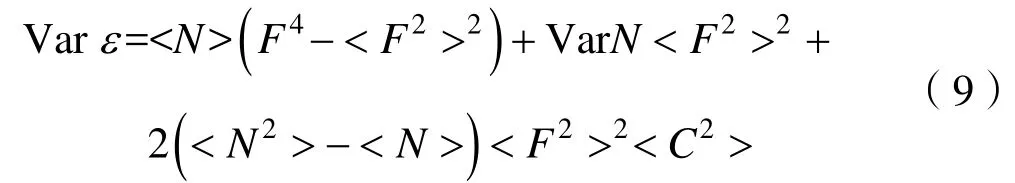
根据泊松混响理论，一般可以假设散射体在水体中服从Poisson分布[3，5-7]，此时测量区间中散射元的数量N满足：

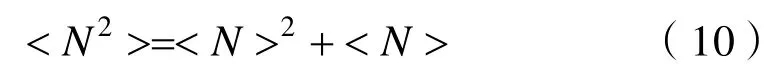
将式（10）代入式（9），可得：

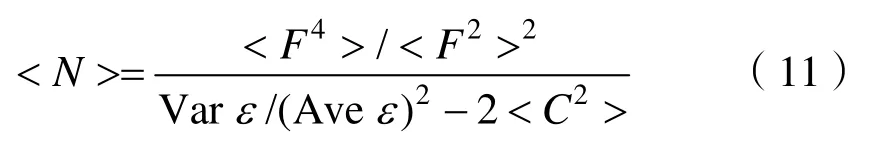
参数 ＜C2＞与测量区间内散射体的分布特征及发射信号的脉宽有关，在一般性条件：t2- t1≫Tp、t1≫Tp、Tp≫1/f0下求 ＜C2＞的近似表达式，满足：

实际上式（5）与式（11）分别建立了散射元的数量与回波信号能量一阶统计量与二阶统计量之间的关系模型。其中式（5）即传统回波积分理论的变形式，该式中的参数为散射体群中单个散射元回波信号幅度的二阶矩，该参量是一个有量纲的绝对量，需要对其进行先验测量。式（11）中的参量是与散射元回波幅度分布有关的一个无量纲的相对量，从统计的角度而言，一般散射体群中散射元的尺寸比较相近，尺寸特别大与特别小的散射元所占的比例很小，一般可用正态分布来对其进行描述[8-9]。此时散射元回波信号幅度的分布满足瑞利分布，可计算得 ＜F4＞ /＜F2＞2=2。另外，式（5）中统计特征量为能量的期望，该特征量为有量纲量，即需要准确计算各个测量时刻回波信号的绝对声能量，因此应用中对声呐系统参数与声传播损失的校准提出了较高要求。而式（11）中的统计特征量是回波能量变异系数，该特征量是归一化的无量纲量，应用中仅需计算回波信号的相对能量即可。即式（1）中回声信号可以是换能器输出的原始电压信号，而不必是真实的声压信号，从而可以避免声源级、换能器接收灵敏度等参数误差对评估结果的影响。

2 仿真与结果分析

本节通过仿真对该模型的性能进行分析。仿真条件如下：

1）选择距离声呐30～40 m的波束照射区域为测量区间；

2）测量过程中各散射元做无规则随机运动，在测量区间内呈均匀随机分布，其总数量的波动变化服从泊松分布；

3）不同测量时刻散射元的散射幅度波动变化，服从瑞利分布；

4）该评估模型与声呐发射信号的频率无关，但不失一般性，本文选择常用的声呐探测信号频段200 kHz作为仿真信号的中心频率，并分别取信号脉冲宽度为0.1 ms与0.4 ms两种CW信号作为探测信号。

2.1 回波能量的统计特性仿真

对处于随机运动状态散射体群的回波数据进行连续仿真，然后利用式（2）计算各帧回波的能量，并利用核函数曲线拟合方法求各信号参数下归一化能量的概率分布曲线，结果如图2所示。

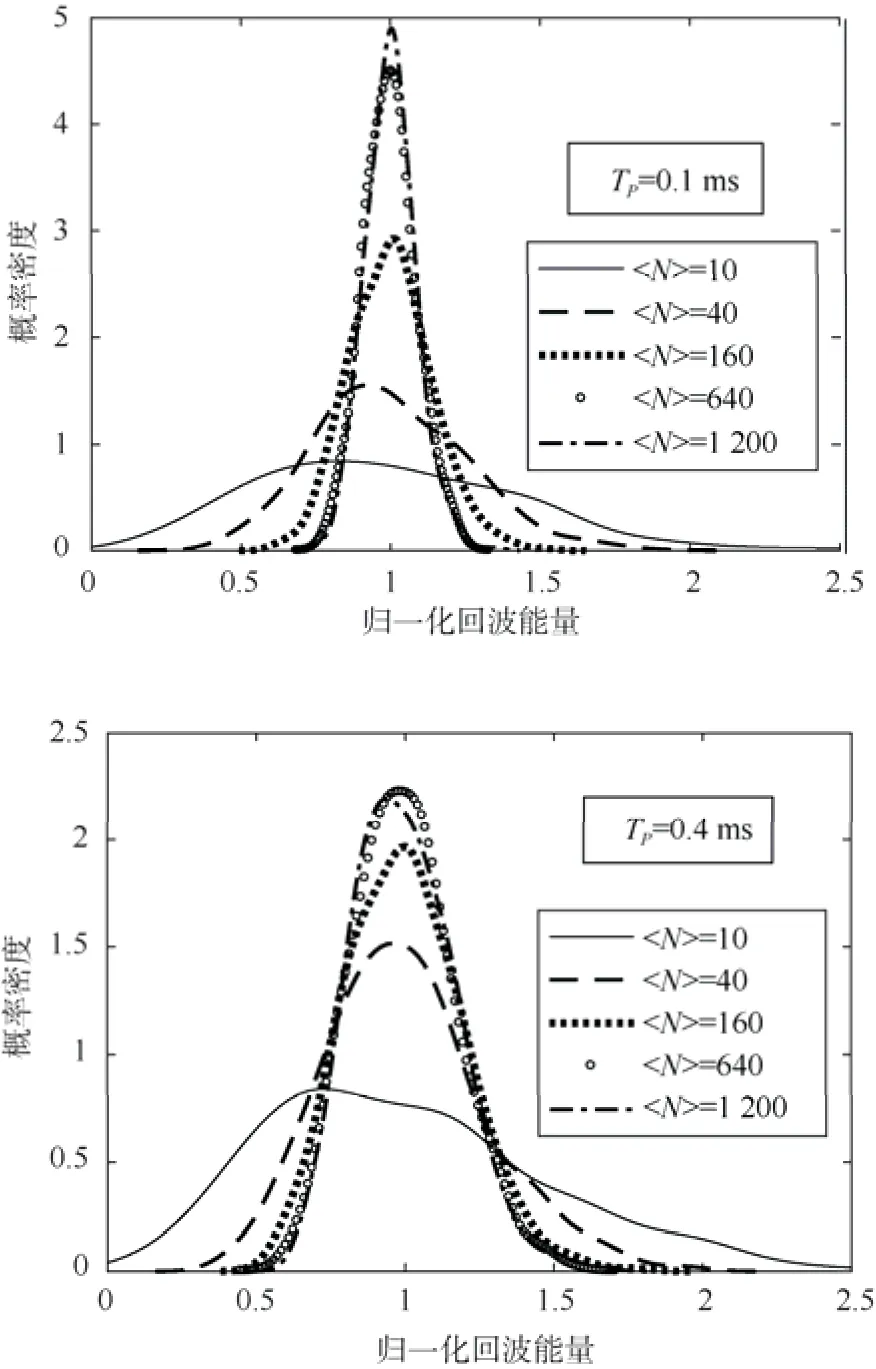
图2 不同条件下回波信号归一化能量的分布Fig.2 Distribution of normalized energy of echo signals under different conditions

可以看出不同散射元数量密度条件（测量区间体积不变）下，散射体群回波信号归一化能量的分布不同，表现为散射元数量密度越小，归一化能量概率密度分布越发散。

而随着散射元数量密度的增大，归一化能量分布由发散逐渐变得集中；当测量区间内散射元的数量增加到某一极限值时，归一化能量概率分布基本不再变化。

另外，从2图对比可以看出，减小发射信号的脉冲宽度有利于提高不同散射元数量密度条件下归一化能量概率密度分布曲线的分辨程度。

利用以上方法，进一步对统计特征量Var /ε(Ave ε)2进行分析，结果如图3所示。

图3 归一化能量与散射元数量的关系Fig.3 Relation between normalized energy and scattering element quantity

由中心极限定理容易理解，随着散射元数量的增大，回波幅度会趋近于高斯分布，且其分布的均值随着散射元数量的增大而增大，而方差随着散射元数量的增大而减小。当散射元数量足够大时，回波信号幅度满足正太分布，此时 V ar ε/ ( Ave ε)2将不再随着散射元数量的变化而明显变化。而相同散射元数量条件下，信号脉冲宽度越小，散射体群回波的重叠程度就越小，其回波信号偏离高斯分布的程度就越大，更有利于在高散射元数量密度条件下维持散射元数量与统计特征量的单调递减关系。这就是图 3中统计特征量随着测量区间内散射元数量的增加单调递减，和图2中利用窄脉冲宽度更有利于散射元数量密度评估的原因。

2.2 评估效果示例分析

在以上仿真条件下，对该方法散射元数量评估效果进行仿真示例分析，结果如图4所示。

可以看出在散射元数量较少的情况下，两类信号均能获得很好的评估效果。随着散射元数量的增加，以脉冲宽度为0.4 ms的CW信号为探测信号时，该方法评估结果逐渐偏小，而脉冲宽度为0.1 ms的探测信号则能在更大散射元数量密度下获得很好的评估效果，这与 2.1节中的分析是一致的。

图4 两种信号条件下评估效果示例Fig.4 Example of estimation effect under two signal conditions

2.3 误差分析

由于散射体活动的随机性，能量统计特征量统计结果的稳定性与统计中所用样本的数量有关。实际上随着测量区间内散射元数量的增加，评估模型表达式的分母V ar ε/ ( Ave ε)2- 2＜C2＞将逐渐接近于0，若统计样本量偏少，多次测量中评估结果将出现较大波动，甚至可能出现明显偏大和负数这样的无效值，这也是图4中评估结果起伏震荡的原因。以测量区间内散射元数量为400，探测信号脉冲宽度 0.1 ms为仿真条件，对统计样本量分别为100与300时500次独立仿真评估结果的分布进行分析，结果如图5所示。

图5 不同样本量条件下评估结果的稳定性Fig.5 Stability of evaluation results under different sample size conditions

可以看出样本量为100时，多次独立仿真评估结果发散程度比较大，当样本量达到300时，评估结果能更好地收敛于真实值参考线附近。

3 结束语

本文针对水下泥沙、气泡、鱼群等数量密度评估问题，考虑这类水下目标的声学散射特征，建立一种基于回波能量统计的散射元数量密度评估模型。该模型仅需对回波信号的相对能量进行统计计算，避免了声呐参数校准误差对评估结果的影响。仿真结果表明，该模型更适用于散射元数量密度较小的情形，且通过减小探测信号的脉冲宽度和增大统计的样本量有利于提高该模型的评估精度。