基于元优化的KNN入侵检测模型

沈焱萍， 伍淳华， 罗 捷, 高方平

(1.防灾科技学院信息工程学院， 北京 101601；2.北京邮电大学网络空间安全学院， 北京 100876；3.国家知识产权局专利局专利审查协作四川中心， 成都 610213)

随着Wannacry等勒索软件的爆发，网络安全问题越来越受到人们重视. 传统的网络安全防御技术，如防火墙、访问控制、加密技术等，难以全面保护网络和系统安全[1-2]. 入侵检测系统(intrusion detection system，IDS)作为一种积极主动的检测工具一直是学术界和工业界研究的热点.

根据检测策略不同，入侵检测技术可分为异常检测、误用检测、特征检测和混合检测，还可按照基于时间、数据来源、系统部署等对入侵检测技术进行分类. 入侵检测常用方法包括基于人工神经网络、基于模糊系统、基于进化计算、基于人工免疫系统等方法[1]. 目前，国内外对基于机器学习方法的入侵检测技术研究达到比较成熟的阶段，然而异常检测仍然遭受低检测率和高误报率的困扰. 值得一提的是，一些机器学习方法必须经过优化才能发挥其理想效果. 例如：支持向量机 (support vector machine, SVM)被证明是一种有效的检测算法，但是它的性能取决于核参数和惩罚系数的选取；极限学习机 (extreme learning machine, ELM)由于其高速的执行效率也受到一些研究者的青睐，但它的性能取决于输入层权重、偏置和隐藏层神经元个数的选取.K-近邻(K-nearest neighbor, KNN)算法也是应用于入侵检测领域较多的方法. KNN在使用中面临2个基本问题：一是距离度量问题；二是参数K的选取问题. 对于距离度量问题，KNN算法需要计算测试样本和每一个训练样本间距离，导致算法复杂度随样本数量线性增加，这给KNN算法在现实中的应用，尤其是处理大数据问题带来挑战. Deng等[3]提出将KNN方法扩展至大规模数据问题处理中，提出通过增加训练过程将聚类算法融入到KNN中. 将大量数据聚类后，在测试阶段只需考虑测试数据和聚类后的每组数据中心的相似度，不需对每一训练数据计算相似度，节约了计算成本. Maillo等[4]利用云平台技术解决大数据问题带来的困扰，针对Hadoop MapReduce框架在设计可扩展机器学习中存在的局限性，提出一种在Apache Spark环境下实现的迭代的基于MapReduce的KNN算法. Spark通过使用内存原语执行分布式计算的速度更快. 参数K的选取方法主要包括2种：1) 为所有测试样本分配固定的专家预定义的最佳K值；2) 为不同测试样本分配不同的最佳K值. Zhang等[5]提出一种kTree方法，通过在KNN分类中增加训练阶段为不同的测试/新样本分配不同的最优K值.

对于距离度量问题，一般选取欧氏距离作为基本的距离度量，在计算两点间距离时，传统KNN 赋予所有特征相同的权重，而在多特征问题中，这种做法是不可取的，目前存在一些针对KNN的特征权重调整方案[6-10]. Chen等[6]提出基于粒子群优化算法的KNN权重学习方法；Tahir等[7]采用禁忌搜索(tabu search, TS)算法进行特征选择的同时对特征权重和KNN参数K进行调整；李峰等[8]提出一种基于互信息的粒化特征加权多标签分类的KNN学习算法，将标签间的相关性融入到特征权重系数的计算中. 以上研究的均是在通用领域KNN的权重调整问题，缺少针对性，而且并没有体现某种智能启发算法的优势. KNN在入侵检测领域被广泛使用[9-16]. Su[9]提出一种实时异常检测模型，由于是实时检测，所用特征均是数据包头部信息的简单抽取，不包含其他统计信息，这对全方位的攻击检测是不可取的；Su等[10]提出基于遗传算法和KNN的DoS/DDoS入侵检测模型，根据特征权重大小选取排序靠前的特征数据做测试. 上述工作[9-10]都是基于遗传算法的KNN权重调整方案进行的DoS攻击检测，不包含其他种类的攻击检测. Aburomman等[11]将SVM模型和KNN模型通过粒子群优化算法构建集成模型进行攻击检测；Li等[12]提出一种基于KNN的无线传感器网络的入侵检测模型；Meng等[13]设计了一种基于KNN的智能报警滤波器，以滤除不必要的报警；Tsai等[14]和Lin等[15]提出的网络特征提取方法，将KNN作为一种典型的入侵检测模型进行分类. 文献[11-15]只是当参数K取不同值时对模型进行评估，并没有考虑不同特征权重对模型结果的影响. Su[16]提出基于遗传算法的加权KNN洪水攻击的异常检测分类器，采用聚类方法减少冗余样本，提高检测效率. 本文重点研究的是基于智能启发算法优化特征权重的KNN入侵检测模型.

智能启发算法对初始条件没有特殊要求，不需要精确的数学模型，对目标函数的可微性也没有要求，不需要领域先验知识，具有较好的黑盒优化能力，在设计机器学习算法框架中发挥重要作用[17-19]. 常见的智能启发方法包括遗传算法 (genetic algorithm, GA)、粒子群优化(particle swarm optimization, PSO)算法、差分进化(differential evolution, DE)算法等. 无免费午餐定理[20]指出：一个特定的智能启发方法可能在一组问题上显示出较好的结果，但在另一组问题上可能表现出较差的性能，即所有优化方法在众多应用场景中的平均性能是相等的. 因此，研究基于不同优化算法优化入侵检测模型具有重要意义.

由于优化方法在诸多方案框架中扮演的是辅助角色，大多数研究者的研究重心往往是主体模型设计，对于优化方案的选取没有深入研究. 为了探究入侵检测领域KNN模型优化问题，本文提出一种基于局部单峰采样的元优化特征权重的KNN入侵检测模型. 元优化(meta-optimization)是指使用一种优化方案调整另一种优化算法的方法，和它类似的有超启发式(hyper-heuristics). 超启发式方法采用启发式算法驱动其他启发式方法，而元优化采用各种控制策略(静态函数甚至是启发式)对问题进行优化. 超启发式是更具有包容性的元优化的一部分[21]. 由于差分进化算法的性能严格依赖于算法相关参数的选取，所以选用局部单峰采样方法确定其相关参数，即本文提出的元优化方案. DE算法[22]是由Rainer Store和Kenneth Price于1997年提出的，基本思想是：应用种群个体差异对种群进行重组，采用父代和子代竞争方法获得新的种群. 与遗传算法相比，该算法待选参数少，有较强的局部搜索能力，是一种较好的智能启发搜索算法. 因此，本文重点研究基于差分进化算法的权重调整方案，采用一种局部搜索算法来确定差分进化算法相关参数并使其更精准地进行寻优工作. 考虑到无免费午餐定理，将该算法和其他常用优化算法包括GA、PSO算法和灰狼优化(grey wolf optimization，GWO)算法进行比较.

1 背景

1.1 KNN算法

KNN算法是一种懒惰式的基于样本的机器学习算法，由于其理论简单，易于实现，不用提前训练等优点，一直是学者们研究的热点. KNN属于有监督分类技术，不像SVM，可直接解决多分类问题.

在KNN分类过程中，训练数据表示为(xi,yi),其中xi=(xi1,xi2,…,xiD)∈RD,xi表示样本特征空间，yi表示样本标签，D表示特征维数. 测试样本所属类别由其周边大部分训练样本所属类别决定，KNN算法中的K即表示特征空间中测试样本周边训练样本点的个数，因此，参数K的选取对KNN算法的分类效果至关重要. 在评估样本距离时，用的最多的是欧氏距离

(1)

在实际应用中，当测量样本间相似度度量时，不同特征的重要性往往是不同的，可以通过给每一维特征赋予一定权重来表示该特征的重要性，因此，样本间欧氏距离可表示为

(2)

式中：wk表示第k个特征的特征权重；dF(xi,xj)表示在不同的特征权重下样本xi和xj间的欧氏距离.

1.2 差分进化算法

DE算法主要应用于连续数据的优化问题，包括个体的变异、交叉和选择等过程，基本步骤如下.

步骤2对种群中的每个个体，随机生成多个互不相同的整数，按任意一种变异策略生成变异个体，F为变异因子，r1,r2,r3,r4,r5∈{1,2,…,N}，表示随机生成的整数，Vi,G表示变异个体，i表示当前种群个体序号. 6种变异策略[23]如下：

·DE/Rand/1

Vi,G=Xr1,G+F(Xr2,G-Xr3,G)

(3)

·DE/Best/1

Vi,G=Xbest,G+F(Xr1,G-Xr2,G)

(4)

·DE/RandToBest/1

Vi,G=Xi,G+F(Xbest,G-Xi,G)+
F(Xr1,G-Xr2,G)

(5)

·DE/Rand/2

Vi,G=Xr1,G+F(Xr2,G-Xr3,G)+
F(Xr4,G-Xr5,G)

(6)

·DE/Best/2

Vi,G=Xbest,G+F(Xr1,G-Xr2,G)+
F(Xr3,G-Xr4,G)

(7)

·DE/RandToBest/2

Vi,G=Xi,G+F(Xbest,G-Xi,G)+F(Xr1,G-Xr2,G)+
F(Xr3,G-Xr4,G)

(8)

步骤3变异产生的个体与目标个体按

(9)

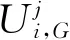
步骤4如果上一步产生的个体适应度优于目标个体适应度，则用试验个体取代目标个体形成下一代[22]

(10)

步骤5重复执行步骤2～4，直到达到最大迭代次数，输出最终最优位置和适应值.

1.3 局部单峰采样

局部单峰采样(local unimodal sampling, LUS)[24]不需要计算导数和梯度，是一种有效的局部搜索算法.

基本思想是在一定范围内对参数进行随机采样，不断减少参数取值范围d直到达到最优解. 采样范围最初覆盖整个搜索空间，随着迭代的增加呈指数级下降. LUS特别适用于只能执行短期运行的优化问题. 初始搜索范围由上限bup和下限blow决定.s=(s1,s2,…,sn)表示最优解，其中n为优化参数个数.s更新方式为

snew=s+a

(11)

式中a是搜索范围内均匀分布的随机向量. 搜索范围更新为

d=qd

(12)

式中减少因子q定义为

(13)

式中β为用户自定义参数.

2 Meta-DE-KNN入侵检测模型

2.1 算法模型

Meta-DE-KNN入侵检测模型整体框架如图1所示. 采用智能启发算法DE对KNN权重进行调整，如图1内部2层所示. DE算法性能受到变异因子等参数的影响，尽管可以通过反复实验进行确定，但通过添加一层优化选择参数会更有效. 因此，采用基于LUS的元优化方法确定DE算法相关参数，即图1外层所示. DE算法的重要参数包括变异因子和交叉概率因子，变异因子设置为某一区间的随机数，交叉概率因子由LUS确定. LUS不需要评估梯度，使用抽样方法通过迭代逐步调整搜索范围来寻找最佳参数.

整体框架如图2所示，一部分数据用来做训练，通过输入优化框架寻找最佳权重；另一部分用来做测试，应用优化框架输出的特征权重基于KNN做最终的预测. 从根本上来说，基于DE优化的特征权重是模型核心部分，以下是基于已知优化参数的DE算法设计，包括种群个体表示和适应度函数定义.

1) 种群个体表示

种群个体由1×D的行向量表示，其中D表示特征维数. 向量中的每一维表示特征权重，由[0,1]范围内的随机数表示，数值越大表示该特征对分类贡献越大，数值越小表示该特征对分类影响较小甚至无影响.

2) 适应度函数定义

差分进化算法是在适应度函数的指引下不断地搜索迭代，最终输出最优解，适应度函数直接影响最优解的质量. 适应度函数的定义由入侵检测模型算法评估参数决定.

Meta-DE优化伪代码见算法1，LUS并不直接生成权重，相反，它通过优化DE参数基于DE间接生成权重，因此，LUS和DE适应度函数相同.

算法1Meta-DE优化算法

输入：迭代次数NoIter1、减少因子q、参数β；

输出：交叉概率因子和特征权重；

初始化: NoIter1，q，β，m;

1. fit = DE (m, train_data, test_data);

2. while iter < NoIter1

3. 在搜索范围内采样新的参数，按式(11)更新；

4. if newFit>fit

5. 更新参数和适应值；

6. Else

7. 按式(12)更新d

8. iter++;

9. end

本文使用标准评估参数评估该模型，应用混淆矩阵得出模型评估参数，混淆矩阵如表1所示. 其中，TP表示攻击样本被正确分类的实例数；FP表示正常样本被判断为攻击样本的实例数；FN表示攻击样本被判断为正常样本的实例数；TN表示正常样本被正确分类的实例数.

模型评估参数包括检测率DR、误报率FPR和准确率Acc，定义[25]如下：

(14)

(15)

(16)

在训练阶段，验证集上的准确率决定目标参数的优劣，适应度函数定义为

(17)

表1 入侵检测中的混淆矩阵

3) 算法流程

本文所用数据集分为训练集、验证集和测试集. 训练集和验证集用来获取最佳特征权重，测试集用来进行最后的测试. 算法首先初始化种群，根据特征权重初始化个体位置. 其次根据个体位置初始化适应度函数，并得到最优个体适应度值. 然后进入差分进化算法种群迭代的主体循环部分，由双层循环表示，外层循环表示迭代次数，内层循环表示种群规模. 在适应度函数的指引下，种群中的个体选择式(3)～(8)中任意一种进行变异操作，根据式(9)～(10)进行交叉和选择操作，当满足一定迭代次数即训练结束后搜索到种群最优位置，输出种群最优解，主体循环部分结束. 最后，根据获得的最优特征权重在测试集上测试从而得到最终实验结果. DE-KNN算法的伪代码见算法2，算法流程如图3所示.

算法2DE-KNN算法

输入：训练集、最近邻参数K、允许的迭代次数NoIter2、变异因子F、交叉概率因子CR、种群数量pop；

输出：混淆矩阵、准确率、检测率和误报率等；

0.初始化: pop， NoIter2，F， CR;K；

1.初始化种群；

2.根据适应值选出最佳个体bestSol；

3.While iter < NoIter2

4. fori=1 : pop

5. 按式(3)～(8)选择任意策略进行变异操作；

6. 按式(9)进行交叉操作；

7. 根据式(10)进行选择；

8. NewSol.Cost = KNN(K, NewSol.Position, train_data, validate_data);

9. if NewSol.Cost > pop(i).Cost

10. pop(i) = NewSol;

11. if pop(i).Cost > bestSol.Cost

12. bestSol = pop(i);

13. end

14. end

15.i++;

16. end

17. bestCost(iter) = bestSol.Cost;

18. iter++；

19.End

20.bestfit = max(bestCost);

21.bestWeight = bestSol.Position;

22. fit=KNN(K, bestWeight, train_data, test_data);

2.2 算法分析

KNN算法复杂度由训练样本个数决定，可表示为O(N)，N为训练样本个数. 差分进化算法属于黑盒优化算法，算法迭代过程有其自身固定的操作环节，算法复杂度主要由适应度函数决定. 基于DE的KNN优化模型的算法复杂度为O(N)×m×NoIter2，其中：m表示种群规模；NoIter2为迭代次数. 假设LUS迭代次数为NoIter1，则算法整体复杂度为O(N)×m×NoIter2×NoIter1.

当前深度学习网络盛行，在图像分析和语音识别方面获得巨大突破. 值得一提的是，参数选取是深度学习算法面临的重要问题，然而采用智能启发算法对其进行优化，虽然在理论上是可行的，但是由于深度学习模型的复杂度和智能启发算法的迭代特性，采用智能启发算法对其进行优化的复杂度将大大增加. 在本文中，KNN属于浅层简单机器学习算法，算法复杂度由训练样本个数决定，而且LUS适用于短期迭代优化问题，因此，选用LUS结合差分进化算法对KNN模型进行优化是可行的.

3 实验结果

3.1 所用数据及实验参数设置

本文选用NSL[26]入侵检测数据集，NSL数据集是由KDD99数据集演变而来的，针对KDD99中存在大量重复记录对分类器性能产生的影响，NSL数据集去除了KDD99中存在的重复记录，与KDD99相比，对分类器性能有更严格的要求. KDD99和NSL有5种类别样本，包含正常数据Normal和攻击数据. 攻击数据分为4类：Probe、DoS、U2R和R2L，每条数据包含传输控制协议(transmission control protocol，TCP)连接基本特征和网络流量统计特征. 本文所用数据从原始训练数据随机抽样得到，并随机分为三部分.T1、T2和T3分别为训练集、验证集和测试集，其中样本类别分布基本遵循原数据集，样本条数分别为4 018、4 017和4 017. 在算法实施前，数据均做了归一化处理.

对于迭代次数和种群数量的选取需保证算法收敛. DE参数设置如下: 最大迭代次数NoIter=120; 群体数目pop=40; 变异因子F是[0.2,0.8]范围内的随机数；采用局部单峰采样优化的变量主要是交叉概率因子，数值取0.2. 实验平台部署环境为Windows操作系统，主频2.4 GHz，32 GB内存，所有实验均在matlabR2012a平台实现并运行.

3.2 Meta-DE-KNN参数K及变异策略选取

参数K的选取直接影响KNN的检测结果，表2～4分别给出了K=1，3，5时基本KNN和6种变异策略下的Meta-DE-KNN在NSL数据集上的实验结果. 所有数据均为10次随机抽取数据的平均值. 最佳实验结果以黑体显示.

表2 K=1时KNN、Meta-DE-KNN的实验结果

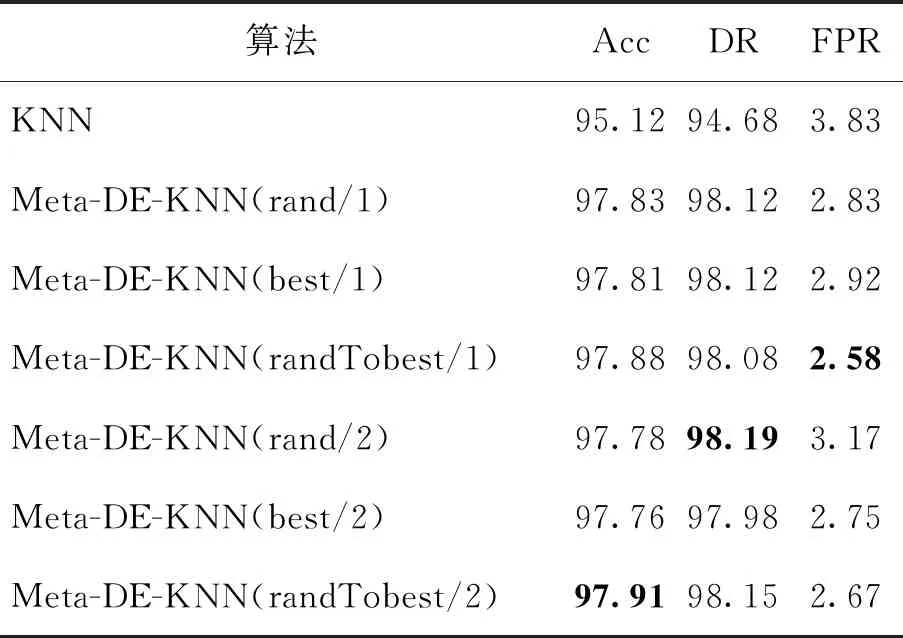
表3 K=3时KNN、Meta-DE-KNN的实验结果

表4 K=5时KNN、Meta-DE-KNN的实验结果

由表2～4可知，不管K取1、3或5，基于Meta-DE优化的KNN检测模型均优于传统的KNN模型. 其中当K=1时，Meta-DE-KNN(randTobest/2)的效果最好，如表2加粗字体所示；当K=3时，Meta-DE-KNN(randTobest/2)的准确率最高为97.91%；当K=5时，Meta-DE-KNN(rand/2)的准确率和检测率最高，分别为97.73%和98.12%. 综上，当K=1时，Meta-DE-KNN的效果最佳，其中变异策略为randTobest/2时，准确率、检测率和误报率最理想，以下均采取此参数K和变异策略进行实验.

3.3 不同智能启发算法优化下的权重优化

无免费午餐定理不仅适用于众多机器学习分类算法，对于优化算法同样适用. 如今存在大量启发优化算法，而且还有其他智能启发算法不断被提出，由无免费午餐定理可知，研究针对某领域的最佳优化算法具有重要意义. 因此，本节研究基于KNN特征权重优化的最佳智能优化算法.

因为存在一些基于GA的KNN权重调整方案进行的DoS攻击检测，所以本节将基于GA和DE对KNN优化并进行比较. 另外，PSO作为启发智能算法应用最多的一种，本节也将考虑基于PSO的KNN权重调整方案，同时GWO算法[27]作为一种新的群智能搜索算法也被考虑进来. 因此，4种优化方案迭代过程如图4所示. 其中蓝色、红色、绿色和黄色曲线分别表示基于Meta-DE、GA、PSO和GWO优化算法的迭代过程. 在初始阶段，GA在短时间内获得比DE更好的适应值，但是随着迭代次数的增加，基于Meta-DE优化的KNN模型准确率超过基于GA的KNN模型，直到达到算法终止条件，基于Meta-DE的优化模型达到最优并保持稳定. 图4表明PSO相比Meta-DE和GA有更快的收敛速度，在迭代次数小于10时就已经达到一定的优化能力，但是相比Meta-DE算法，在后期不易跳出局部极值点. GWO算法与PSO算法的迭代过程类似，收敛速度较快，但在求解精度上不如PSO算法. 综上，和其他3种优化算法相比，Meta-DE算法不仅具有一定的收敛速度而且在变异策略randTobest/2的指引下易于跳出局部极值，有更强的全局搜索能力.

其次，KNN、GA-KNN、PSO-KNN、Meta-DE-KNN算法和GWO-KNN算法对各类样本检测准确率的比较如图5所示. 总体来看，基于权重优化的KNN性能优于原始模型. 与原始模型相比，GA-KNN对于U2R类型提升比较明显，对于R2L和原算法持平；与GA-KNN、PSO-KNN和GWO-KNN相比，Meta-DE-KNN除了对于U2R没有明显改进，对于其他类型的检测率均有所提升.

将Meta-DE-KNN入侵检测模型和现有文献模型进行比较，包括SVM、ELM、RandomForest (RF)和J48算法在准确率、检测率、误报率三方面的比较. 实验结果表明，基于Meta-DE的优化模型和其他算法相比，性能得到了改善，准确率和检测率得到提升. 其中，RF为多棵决策树的集成，其准确率和误报率略优于Meta-DE-KNN，Meta-DE-KNN的检测率优于RF算法. 表5表明，经过Meta-DE优化的KNN具有一定优势，应用于入侵检测是可行的.

表5 仿真实验结果对比

4 结论

1) 入侵检测作为网络安全的一项重要技术，一直是国内外学者研究的热点，基于KNN的机器学习技术是重要的入侵检测方法. 本文针对基于KNN算法的入侵检测模型检测率低和误报率高的问题, 提出一种元优化模型优化特征权重问题. 实验结果表明，该方法可有效确定相关算法参数并搜索出合适的特征权重，与未进行特征权重优化算法相比能获得较好的分类精度并淘汰冗余或无关的特征.

2) 与其他常用智能启发算法优化KNN模型进行比较，实验结果在准确率、检测率和误报率方面都有所改善，与现有的机器学习算法相比也具有一定优势.

3) 如何提高KNN算法执行效率是下一步需要进行的工作，研究DE算法本身的优化，例如：借助其他优化策略提高DE算法的收敛性和精度，也是下一步要考虑的问题.