观测与相对论:光速在爱因斯坦狭义相对论中为什么不变?
阮晓钢
(北京工业大学信息学部, 北京 100124)
1887年,因循麦克斯韦的建议[1],迈克尔逊和莫雷[2]开展了一项旨在捕捉以太(Ether)的实验. 他们没能发现以太,却遇到了一个问题:伽利略速度叠加原理失效了. 迈克尔逊- 莫雷实验显示,光速与地球轨道速度叠加,仍然是光速.
为了解释迈克尔逊- 莫雷实验,菲兹杰拉德提出一个假设[3]:运动物体沿运动方向长度收缩,收缩率为(1-v2/c2);之后,洛伦兹补充一个假设[4-6]:运动物体时间膨胀,膨胀率为1/(1-v2/c2). 于是,洛伦兹变换(或更应该称之为菲兹杰拉德- 洛伦兹变换)诞生了. 1905年,爱因斯坦领悟到迈克尔逊- 莫雷实验的“真谛”:光似乎没有速度叠加效应,相对于所有观测者,光速都是相同的;于是,提出了光速不变性(invariance of light speed, ILS)假设. 正是基于ILS假设,爱因斯坦成功地从理论上推导出洛伦兹变换,建立狭义相对论(special relativity, SR)[7],揭示了时空和物质运动的相对论性现象(relativistic phenomenon).
ILS假设不仅是爱因斯坦SR的基石,同时,也是爱因斯坦广义相对论(general relativity, GR)[8]的前提之一. 一百多年来,爱因斯坦的相对论,包括SR和GR,得到几乎所有观测和实验支持[9-10]. 然而,直到今天,我们仍然并不十分理解光速为什么不变[11-12];并且,也不完全理解时空和物质运动为什么会呈现相对论性现象[13-14].
ILS假设有一直接的推论:光速乃宇宙终极速度,是任何其他的物质运动所不可超越的. 值得注意,爱因斯坦将ILS融入了自己的局域性(locality)观念[15-16]:物质运动速度是有限的,光速是速度上限;宇宙不存在超距作用. 本文将物理可观测性明确地表述为一项基本原理或公理,由此,从逻辑上导出物理世界的局域性(locality of the physical world, LPW). 然而,与爱因斯坦的局域性观念不同,LPW并不意味着光速是宇宙终极速度或不可超越,而只意味着,物质运动速度不能无穷大.
LPW是物理上的局域性,是自然的本质属性. 值得注意的是,物理上的局域性势必导致观测上的局域性:任何为我们传递被观测对象之信息的观测媒介,其速度都是有限的. 自然地,观测局域性制约着我们的观测. 可以设想,我们所能观测的惯性运动速度上限或范围,无法超越观测媒介的速度. 基于这一启发式判断,本文提出观测极限假设(hypothesis of observational limit, HOL),以其为前提,从逻辑上和理论上导出了一个具有重要意义的结论:观测媒介速度不变性(invariance of observation-medium speeds, IOMS),其中,ILS只是一个特例,仅当光作为观测媒介时成立. 恰好,我们的观测和实验大多采用光或电磁相互作用作为传递信息的媒介,这便是ILS假设以及SR和GR得到大多数观测和实验支持的原因. 然而,很显然,光并非所能利用的唯一的观测媒介. 基于IOMS,本文从逻辑上和理论上导出广义洛伦兹变换(general Lorentz transformation, GLT),概括了洛伦兹变换;建立观测相对论(theory of observational relativity, OR),概括爱因斯坦SR. GLT和OR理论阐明了相对论性的本质和根源:光速并非真地不变或不可超越;所有的相对论性现象都是观测效应,源于观测局域性,而非真实的自然现象或物理现实.
我们总是不停地在问,光在洛伦兹变换和爱因斯坦相对论中到底扮演着什么角色,光速为什么不变和不可超越,时空中的同时性为什么是相对的,时间为什么会膨胀,空间为什么会收缩. 毫无疑问,探索和阐明这些爱因斯坦未能解答的基本问题,无论对于物理学还是物理学家,都是一项重要的和重大的任务. 或许,本文的观点和结论能给予我们关于时空和物质运动之相对论性现象以及爱因斯坦相对论新的认识或新的见解.
1 观测与媒介
人类对客观世界的认识,既依赖于观测,又制约于观测. 物理学一切理论或学说,包括伽利略变换和洛伦兹变换,都与观测手段或观测媒介联系在一起,无不打上观测的烙印.
1.1 观测的基本元素
观测的基本任务是利用感官或观测仪器获取被观测对象的信息. 自然地,被观测对象的信息必须借助于一定的媒介,以一定的方式,传递至感官或观测仪器,方能被我们感知或观测.
因此,一个观测体系,可以描述为一个三元组(Σ,M,O),其中,涉及3项基本元素:
1) Σ为被观测对象,即观测信息(observed information, OI)的发射者;
2) M为观测媒介,即OI的传递者;
3) O为观测者,即OI的接收者.
特别注意,在观测体系(Σ,M,O)中,观测媒介M最重要的物理量,是M传递信息的速度,即M的速度:信息源Σ相对于O静止时,M或OI相对于O的速度. 本文将M的速度记作η.
在闵可夫斯基四维时空中,Σ运动的历史脉络是一世界线(world line). 世界线是Σ时序事件的集合,其中,作为四维时空点,每一事件(event)最为基本的信息是其发生的时刻(时间信息)和位置(空间信息),可统称为时空信息(space-time information, STI). Σ之STI便是O意欲获取的有关Σ的最为基本的观测信息(OI).
无论如何,Σ之OI或STI必须借助某种M,由Σ传递至O. 于是,我们会问:在我们的观测中,什么可以担当M呢?
1.2 观测媒介
众所周知,物质具有波粒二象性(wave-particle duality, WPD),运动起来既似粒子又似波. 20世纪20年代,德布罗意基于WPD杜撰了物质波(matter wave)的概念[17-18]. 物质波的概念可以推广至任意物质运动形式,包括声波、水波、光波、电波,甚至一粒电子或一块岩石. 波,具有一种重要的性质:可调制性(modulability),因而具备了携带和传递信息的特质.
理论上,对于一个观测体系(Σ,M,O),任意物质波或任意物质运动形式,均可担当其观测媒介M,作为信息的使者,为观测者O传递被观测对象Σ的时空信息STI或观测信息OI. 光是我们最习以为常的观测媒介. 因为有光,我们能用眼睛看世界.
然而,光,并非唯一可能的观测媒介.
如图1(a)所示,天空有一雷电事件发生,其最基本的信息自然是时空信息,即其发生的时间和位置. 那么,我们怎么测定雷电的时空坐标呢?我们感知或观测雷电,必须依赖一定的媒介为我们传递雷电之时空信息. 就人类感知能力所及,能为我们传递雷电时空信息的媒介,可以是声波,也可以是光波;超越直接的感知,借助人类发明的技术手段,雷电所辐射的无线电波或强脉冲磁场也能作为信息使者,为我们传递雷电时空信息.
传统天文学依靠肉眼和光学望远镜观测天象,其中,传递天体物理信息的媒介是可见光. 射电天文学的发展将观测媒介由可见光扩展至几乎整个无线电频域. 正是射电天文观测发现了宇宙微波背景辐射[19],为大爆炸理论提供了证据[20].
现在,人类对引力波的探测,导致了引力波天文学(gravitational-wave astronomy)[21-22]的概念. 与传统天文学和射电天文学不同,引力波天文学以引力相互作用为观测媒介,而非电磁相互作用.
实际上,在物理观测中,我们可以利用所有可能的M,而不仅仅是光. 因此,我们自然会问:不同的M对于物理观测或观测信息OI的传输有什么不同呢?
1.3 观测上的非即时性
作为物质波,不同的观测媒介有不同的速度. 然而,无论观测体系(Σ,M,O)中的观测媒介M是什么,其速度η必定是有限的;因而,观测信息OI或STI从Σ传输至O必定存在观测上的滞后.
声音在20 ℃的地球大气层中以大约343 m/s的速度传播;我们听见10 km外的雷声时,其观测信息OI或STI已经滞后了几乎30 s. 光速远远高于声速,然而,闪电带给我们的,也只能是滞后的雷电时空信息.
雷电可视为相对于观测者的静态对象;而大多数被观测对象相对于观测者是动态的. 鸟从天空飞过,怎么感知或观测其运动呢?我们能以声为M用耳朵听之,也能以光为M用眼睛观之. 然而,如图1(b)所示,无论声波还是光波,其传递给我们的都只能是滞后的有关鸟的时空信息:我们听见鸟的鸣叫,但它已经不在那鸣叫时的处所;我们看见鸟的身影,但那只是它片刻之前的所在.
这便是观测上的非即时性(non-instantaneity). OI或STI观测上的滞后,即所谓非即时性,与M的速度η相关:η越小,滞后越大,其非即时性越显著. 观测信息的滞后或非即时性制约着我们的观测,并且,势必反映在物理学的理论体系和时空模型中. 事实上,这导致了伽利略变换与洛伦兹变换的差异,以及牛顿理论与爱因斯坦相对论的差异.
注意,观测信息的滞后或非即时性,与物理世界的局域性问题相关,是观测局域性的具体体现,并且,导致了物质运动速度观测上的极限.
2 观测与局域性
局域性(locality),或局域性原理,在现代物理学中扮演着重要角色. 然而,物理学家们很少将物理世界的局域性明确地与物理世界的可观测性联系在一起.
2.1 可观测性
物理世界是可观测的,这种可观测性是人类获取自然知识进而认知客观世界的前提. 本文将物理世界的可观测性(observability of the physical world, OPW)明确地表述为物理学一项最为基本的原理或公理.
OPW原理:任意物理量都是可观测的,其观测值必然是确定的和有限的.
显然,OPW原理是不证自明的,并且,具有作为基本原理和公理的合理性;否则,我们将无法认识和理解客观世界.
物理量是表示物质或物体物理特性的量,可通过观测或测量予以量化. 物理量的数学变换仍然是物理量,仍然需要服从OPW原理. 可见,OPW原理下,物理学理论体系或时空模型中奇点处的物理量不能代表物理现实. 因此,OPW原理可称为奇点原理(singularity principle). 按照Hawking[23]的观点,物理学理论或模型在奇点处崩溃.
OPW原理下,我们能更好地理解物理世界的局域性问题,包括物理上的和观测上的;能更好地理解观测信息之非即时性问题.
2.2 OPW原理下的局域性
爱因斯坦的局域性观念与其ILS假设联系在一起. 爱因斯坦相信:宇宙不存在超距作用,并且,基于ILS假设,无论物质或信息,其运动速度都不能超越光速[15-16]. 1935年,爱因斯坦基于自己的局域性观念,与同事Podolsky和Rosen一起,构思了一个著名的思想实验,史称EPR佯谬[24],以质疑量子力学的完备性. 然而,似乎越来越多的EPR实验支持量子纠缠现象[25-26].
那么,宇宙是否真地存在“鬼魅般的超距作用”(spooky action at a distance)[27]呢?
OPW原理下,物理世界的局域性毋庸置疑. 实际上,物理世界的局域性可从逻辑上由OPW原理导出,并且,表述为如下原理.
物理上的局域性原理(principle of physical locality, PPL):依据OPW,物质运动的速度是有限的,因而,宇宙不存在超距作用.
显然,PPL原理是OPW原理一个直接的推论. 根据OPW原理,物质跨越空间必定需要时间.
然而,与爱因斯坦基于ILS假设的局域性观念不同,基于OPW的PPL原理并不意味着光速是宇宙终极速度和不可超越,而只意味着,宇宙不存在速度无限的物质运动.
值得注意的是,物理上的局域性(physical locality),势必导致观测上的局域性(observational locality),并且,为我们设置观测上的速度上限.
2.3 观测上的局域性
根据OPW原理或PPL原理,观测媒介的速度是有限的. 因此,观测信息跨越空间需要时间. 作为一个推论,如下原理可以从逻辑上由OPW下的PPL原理导出.
观测上的局域性原理(principle of observational locality, POL):任意观测体系(Σ,M,O),其观测媒介M的速度η必定是有限的,即η<∞;因此,观测信息OI由Σ传递至O需要时间.
简而言之,POL原理即:η<∞. POL原理定义了绝对的观测局域性(absolute observational locality):无论M是什么,观测体系(Σ,M,O)都存在观测上的局域性;观测信息OI都存在非即时性,OI传输总会存观测上的滞后或延迟.
2.4 观测极限假设
观测体系(Σ,M,O)之观测上的局域性,即M之速度η的有限性,制约着观测者O的观测. 自然地,不同速度的M导致观测信息OI不同程度的延迟或滞后,此乃相对的观测局域性(relative observational locality):M的速度η越低,(Σ,M,O)所呈现的观测局域性就越显著.
凭经验和直觉,我们可以做出并理解这样的启发式判断:制约于超声波的局域性,蝙蝠不能指望借助于超声波能探测超音速物质运动;制约于光的局域性,人类不能指望借助于光能探测超光速物质运动.
以此类推,我们建立如下假设性逻辑前提.
观测极限假设(hypothesis of observational limit, HOL):设任意观测体系(Σ,M,O)之O为Σ惯性观测者,则其观测媒介M的速度η,是O借助M所能观测到的Σ之速度u的上限,即|u|≤η.
HOL假设意味着,对于任意观测体系(Σ,M,O),其观测媒介M的速度η,限制了观测者O所能观测的惯性速度范围. 想要突破特定观测媒介M的观测局域性,我们必须借助更快的观测媒介.
3 观测媒介之速度不变性
目前,主流学术观点认为,ILS是光作为宇宙终极速度的具体体现,代表着物理现实,是真实的自然现象. 正如Landau等[28]所述:“由于相互作用的局域性,宇宙存在理论上的最大速度,并且,这一速度必定是不变的.”然而,ILS实际上只是一种观测效应,源于光的观测局域性.
3.1 IOMS定律:基于HOL的逻辑结论
事实上,迈克尔逊- 莫雷实验并不意味着ILS,而是向我们展示一个极为重要的物理观测现象:对于观测者而言,观测媒介的速度具有观测上的不变性. 这可以从POL原理和HOL假设导出,并且,可作为一个定律,表述如下.
观测媒介速度不变性(invariance of observation-medium speeds, IOMS)定律:观测媒介的速度具有观测上的不变性,即相对于所有的惯性观测者都是相同的,与观测者和被观测对象的运动无关.
更形式化地,IOMS定律可表述为:
令(Σ,M,O)和(Σ,M′,O′)为被观测对象Σ的任意2个惯性观测体系,Σ在O和O′中分别以惯性速度u和u′运动,O′以惯性速度v相对于O运动(或者说,O以惯性速度-v相对于O′运动). 如果M和M′为相同观测媒介,那么,其速度η相对于O和O′是不变的或相同的.
IOMS定律意味着,观测媒介的速度不具有叠加效应:M的速度η叠加任意惯性速度仍然是η.
证明:除了POL原理和HOL假设之外,我们还需将相对性原理(principle of relativity)作为IOMS定律的前提,并且,假设O和O′间的相对运动速度小于M的速度η,即|v|<η.
Σ和M以及O和O′之间的相对运动关系如图2所示. 根据物质运动的基本物理性质,惯性速度u和u′以及v之间必然存在一定的叠加关系:Σ在O中的速度u,应该是Σ在O′中的速度u′与O′相对于O的速度v的叠加(u=u′⊕v);而u′应该是u与O相对于O′的速度-v的叠加(u′=u⊕(-v)). 于是,我们基于物质运动的基本物理性质,以及数学运算的基本法则,可如下定义速度叠加算子‘⊕’:
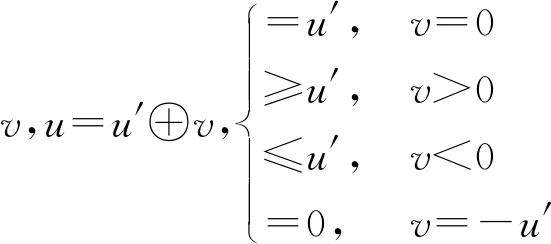
(1)
相对性原理下,当观测体系(Σ,M,O)和(Σ,M′,O′)拥有相同观测媒介(M=M′)时,其观测时空(observed spacetime)是对称的,O和O′平权,其物理学定律应具备相同形式. 因此,对于速度叠加算子“⊕”,必然成立如下逆运算法则:
ifu=u′⊕v, thenu′=u⊕(-v)
(2)
根据POL原理,η<∞,因而,可令|u′|=η. 利用式(1),当u′和v同方向时
|u|=|u′⊕v|=|u′|⊕|v|=η⊕|v|
(3)
成立.
由式(1)和式(3)可得:|u|≥η;由HOL假设可得:|u|≤η. 因此,|u|=η;式(3)可重新写作:η=η⊕|v|. 根据式(2), 若|v|<η,则η=η⊕(-|v|).
于是,我们得到
∀v∈(-η,η),η⊕v=η
(4)
式(4)表明,M的速度η在惯性时空中无叠加效应,是不变的,相对于O和O′是相同的. 可见,IOMS定律在POL原理和HOL假设下成立.
□
IOMS定律是HOL假设的逻辑结论. 本文中,HOL假设只是一个源于经验和直觉的启发式判断. 然而,在电子预印本[29-30]中,HOL和IOMS都是以时空和物质运动之更基本物理性质为前提导出的逻辑结论.
3.2 IOMS的寓意
在IOMS定律下,我们能更好地理解ILS假设和相对论性效应(relativistic effect). IOMS定律具有深刻寓意. 让我们从一些基本的问题开始对其进行讨论.
IOMS能给予ILS什么新的见解?
IOMS概括了ILS. 现在,ILS不再是一个假设,而是IOMS定律的一个推论,一个特例;并且,可重新表述如下.
光速不变性(ILS):在以光为观测媒介的观测体系中,光速相对于所有观测者都是相同的或不变的.
特别注意,其中的光速是光在观测时空中的传播速度,未必是c,除非观测时空即真空. 或者说,仅当光担任观测媒介而观测时空为真空时,爱因斯坦的ILS假设才能成立.
为什么光在迈克尔逊- 莫雷实验中看似不变?ILS或IOMS是真实的自然现象吗?
IOMS定律揭示了爱因斯坦ILS假设的本质.
在迈克尔逊- 莫雷实验[2]中,光,既是被观测对象(Σ),同时,又是传递观测信息OI的观测媒介(M);因而,此时的光速在观测上(看起来)是不变的. 有关ILS的其他观测和实验,比如光行差现象[31-32]和Kennedy-Thorndike实验[33],其情形也如此. 实际上,光速并非真地不变.
IOMS定律表明,所有的物质运动或物质波,而不仅仅是光,都能作为信息的使者. 不同的物质波有不同的速度. IOMS定律下,任意物质波,当其担当观测媒介的角色时,其速度对于观测者而言都是不变的. 可见,IOMS,以及作为其特例的ILS,都只是观测效应,而非真实的自然现象.
特别注意,ILS假设是爱因斯坦SR的前提,这或许意味着,SR(甚至GR)中的所有相对论性现象都只是观测效应,并不代表物理现实.
IOMS定律下,什么是不变速度?不变速度是宇宙终极速度吗?
所谓不变速度(invariant speed),指相对于所有惯性观测者都相同的速度. 目前,物理学家们普遍认为,不变速度必定是宇宙的终极速度,是不可超越的;并且,根据爱因斯坦ILS假设,这一速度就是真空中的光速c.
然而,IOMS定律表明,不同的观测体系有不同的不变速度:牛顿力学暗示信息传输不需要时间,因而,其不变速度无穷大;爱因斯坦SR暗示光或电磁相互作用是信息的使者,因而,其不变速度乃光速;而蝙蝠的超声波回声定位系统中,超声波担当信息媒介,因而,其不变速度乃大气中的声速. 可见,如此看似不变的速度,并不能代表宇宙终极速度,而只是观测效应. 根据IOMS定律,物理世界不存在真实的不变速度,因而,也不存在所谓的终极速度.
值得注意的是,“不变速度”一词对于IOMS和ILS有不同的含义.
在爱因斯坦的ILS假设和SR(甚至GR)中,不变速度被强制定义为c=299 792 458 m/s,即光在真空中传播的速度,与光源和惯性观测者的运动无关. 然而,IOMS定律下,一个观测体系(Σ,M,O)中的不变速度被定义为:被观测对象Σ(信息源)相对于观测者O静止时,观测媒介M相对于O的速度. 因此,对于以光为媒的光学观测体系,不变速度则是光源静止时光相对于O的速度,未必是c,除非O的观测时空为真空.
IOMS能给予相对性原理什么新的见解?
相对性原理[7,34]意味着:惯性时空是对称的,所有的惯性观测者或惯性参考系是平权的;因而,物理学的定律在所有的惯性参考系中具有相同的形式. 爱因斯坦将这一原理推广至非惯性系,即所谓广义相对性原理(general principle of relativity)[8,34]:所有参考系在物理学基本定律的表述上都是等价的.
真实的客观时空可能或者应该是对称的. 然而,IOMS定律下,观测时空未必是对称的. 制约于观测或观测媒介,大自然所能呈现给我们的,只能是观测时空,而非客观时空. 根据IOMS定律,观测时空的对称性是有条件的,取决于观测者或观测体系是否采用相同的观测媒介,与参考系是否为惯性系无关. IOMS定律表明,2个观测体系(Σ,M,O)和(Σ,M′,O′)是对称的,因而在物理学基本定律的表述上等价,或者,观测者O和O′在观测时空中平权,仅当它们的观测媒介M和M′相同时.
可见,我们理所当然地认为相对性原理是有条件的:仅当观测者借助相同观测媒介观测客观世界时,相对性原理才能成立.
IOMS有观测或实验支持吗?或者,IOMS能通过实验验证码?
物理学在很大程度上是一门实证科学,其理论或学说的正确性或有效性,终究需要通过观测和实验而非理论的验证或检验.
ILS假设是爱因斯坦SR的基石,然而,SR不能解释光速为什么不变. 物理学家们相信ILS,是因为光速在我们的观测和实验中显现出不变性. 实际上,这些观测和实验,包括Bradley对光行差的观测[31],以及迈克尔逊- 莫雷实验[2],与其说是为ILS假设不如说是为IOMS定律提供了实证依据,其中,光或电磁相互作用扮演着观测媒介的角色,于是,ILS便成为IOMS的一种具体体现.
或许,在IOMS定律下,我们可以通过实验,测试亚光速媒介(比如电子波或电子波)的速度不变性,或者,甚至测试超光速媒介(比如引力子或引力波)的速度不变性.
4 广义洛伦兹变换
洛伦兹变换是一种时空变换模型,其中,光被隐喻为观测媒介(M),而观测信息OI的传播速度(η)被隐喻为c,即光在真空中的传播速度. 然而,值得注意的是,在我们的物理观测中,M并非只能是光,η并非只能是c. 现在,ILS假设被IOMS定律所概括;基于IOMS定律,洛伦兹变换可自然地被推广至任意M或任意η.
4.1 ILS假设与洛伦兹变换
人们已经意识到,相对论性并不取决于光的物理性质;主流观点认为,相对论性现象源于物理世界的局域性和时空的对称性[35]. 因此,无须ILS假设,仅从局域性和对称性出发,也能导出洛伦兹变换和爱因斯坦SR[36-37]. 在群论中,基于时空的对称性和均匀性,洛伦兹变换被泛化为洛伦兹群[38],乃至庞加莱群[39].
群理论将洛伦兹因子γ=1/(1+v2/c2)泛化为:Γ=1/(1+κv2),其中,在群论之公理下,κ没有明确的物理意义;一般归纳为3种可能的情形:
第一,κ>0,与物理现实不符;
第二,κ=0,Γ=1,属非相对论性,与SR不符;
第三,κ<0,Γ>1,符合SR,需实验确定κ.
鉴于物理世界的局域性,主流观点认为,时空必定存在某个确定的κ值(如第3种情形所示):κ=-1/Λ2<0;并认为,Λ应该是一个宇宙常数,代表宇宙“终极速度”(theultimatespeed),并被视为“不变速度”(invariantspeed),需要通过实验来标定. 基于爱因斯坦的ILS假设,人们相信:Λ=c. 正如Landau等[28]所言:“结果证明,这一速度恰好就是真空中的光速.”
上述推论将“极限速度”视为“不变速度”是一种错误!事实上,根据IOMS定律,宇宙并不存在所谓的“不变速度”或“终极速度”. 基于时空的局限性,可以得出这样的结论:第一,所有物质运动形式之速度都是有限的;第二,其中必有某种物质运动形成的速度是最大的. 然而,这种“最大速度”并非“不变速度”.
Landau等已经意识到c在洛伦兹因子γ中代表信息传递速度(speed of information transmission)[28]. 然而,物理学家们似乎并未认真思考,在观测和实验以及物理学的理论或模型中,信息传递速度能否不同于真空中的光速c;更没有认真思考,观测信息是否能由不同于光的媒介传递.
4.2 IOMS定律与GLT
在IOMS定律下,直接地以观测媒介M之速度η替代洛伦兹变换中的光速c,可得GLT. 然而,为了更好地理解GLT中参数的物理意义,我们因循爱因斯坦SR逻辑[7],以IOMS定律替代ILS假设,演义“GLT”.
GLT与洛伦兹变换一样,是相对论性的时空变换模型. 相对论性效应意味着,时间与空间相互依存,不可分割. 于是,时间(time)与空间(space)统一起来,便形成了时空(spacetime)的概念. 不同观测体系代表不同时空;图3中的2个观测体系(Σ,M,O)和(Σ,M′,O′)可谓被观测对象Σ之2个不同的惯性时空,其时空变换可记作:O′→O和O→O′. 自然地,(Σ,M,O)和(Σ,M′,O′)之间的变换是有条件的.
观测时空变换条件:对于惯性观测体系(Σ,M,O)和(Σ,M′,O′),O和O′的观测时空可变换,当且仅当M和M′为相同的观测媒介,因而,观测者O和O′是平权的,观测时空是对称的.
GLT的逻辑前提条件:
第一,简单性原理(principle of simplicity);
第二,相对性原理(principle of relativity);
第三,IOMS定律(而非ILS假设).
如图3所示,我们定义一个以Σ为原点的三维笛卡儿(自由)坐标系Oo. 自然地,Oo是Σ的一个固有惯性系,而Σ任何其他的惯性系(包括O和O′)皆可相对于Oo定义. 假设在Y(或Y′)和Z(或Z′)方向上,O和O′之间无相对运动,那么,Y=Y′且Z=Z′;因而,我们只需要考虑O和O′在X(或X′)方向上的相对运动. 不失一般性,假设:如图3(a)所示,t=t′=0时,Σ与O和O′重合;如图3(b)所示,t>0且t′>0时,Σ以速度u在O中沿X轴方向运动,以速度u′在O′中沿X′轴方向运动,O′以速度v相对于O沿X轴方向运动,或者说,O以速度-v相对于O′沿X′轴方向运动.
因循爱因斯坦SR中的逻辑线路,我们将GLT的逻辑演绎过程划分为3段.
第一,基于简单性原理.
事实上,除ILS假设和相对性原理外,爱因斯坦SR[7]还有一项前提:简单性原理[40-41]. 基于简单性原理,我们可以设时空变换O′→O的形式为简单的线性形式
x=Γx′+bt′
(5)
爱因斯坦将这种线性关系归因于时空的均匀性或同质性(homogeneity)[7].
时间与空间的基本关系要求:若x=0则x′=-vt′. 因此,b=Γv;式(5)可进一步简化为x=Γ(x′+vt′).
第二,基于相对性原理.
当观测媒介M和M′相同时,根据相对性原理,(Σ,M,O)和(Σ,M′,O′)具有对称性,时空变换O→O′应具有与O′→O相同的形式:x′=Γ(x-vt′). 联立空性式x=Γ(x′+vt′)和x′=Γ(x-vt′),可得时性式:t=Γ(t′+(1-Γ-2)x′/v)和t′=Γ(t-(1-Γ-2)x/v).
于是,根据Σ在O和O′中的速度定义,成立
(6)
第三,基于IOMS定律.
假设M的速度为η.
在IOMS定律下:若u′=η,则u=η. 代入式(6)可得GLT之时空变换因子
(7)
简称GLT因子,其中,η具有清晰而明确的物理意义,代表M传递观测信息OI的速度. 值得注意的是,η取决于O和O′所借助的观测媒介M,并非确定的宇宙常数,并且,未必是c.
现在,归纳起来,我们便得到如下GLT关系:
(8)
式(8)所示的GLT,概括了洛伦兹变换,并且具有与洛伦兹变换完全相同的形式. 因而,基于洛伦兹变换的爱因斯坦SR,可基于GLT,自然而符合逻辑地进行概括或推广.
4.3 时空变换的统一
伽利略变换和洛伦兹变换是物理学两大时空变换关系. 统一伽利略变换和洛伦兹变换,对于物理学,无疑具有重要意义.
在洛伦兹变换中,光扮演着观测信息之信使的角色. 然而,在GLT中,光并非唯一可能的观测媒介. 理论上,任意物质运动或物质波,如声波、电子流、脉冲磁场、引力波,甚至被观测对象自身,都能成为观测媒介. GLT表明,不同的观测体系可能导致不同的时空变换. 伽利略变换,是理想观测体系(η→∞)的产物,其中,M的速度η被隐喻为无穷大,因而,不存在观测局域性. 洛伦兹变换是光学观测体系的产物,其中,M被隐喻为光,而η被隐喻为c.
现在,GLT概括并统一了伽利略变换和洛伦兹变换. 在波尔对应原理(Bohr’s correspondence principle)[42-43]下,GLT与伽利略变换严格对应:当η→∞时,GLT蜕化为伽利略变换
(9)
同时,GLT与洛伦兹变换严格对应:当η→c时,GLT蜕化为洛伦兹变换
(10)
特别注意,主流学术观点认为,洛伦兹变换与伽利略变换在波尔对应原理下具有对应关系. 实际上,洛伦兹变换与伽利略变换并不严格对应,仅在v≪c时近似,即
(11)
GLT与伽利略变换以及洛伦兹变换的严格对应,从一个侧面印证了GLT之逻辑上的合理性及其理论上的有效性.
5 相对论性效应的本质和根源
IOMS定律阐明迈克尔逊- 莫雷实验中的光速为什么不变;而GLT则进一步阐明时空和物质运动为什么呈现相对论性效应.
爱因斯坦相信:时空和物质运动本质上是相对论性的(relativistic). 然而,GLT表明,相对论性现象只是一类依赖于观测并制约于观测媒介速度的观测效应. 在爱因斯坦SR中[7],最著名、最经典的相对论性现象当属时涨尺缩(time dilation and length contraction, TD&LC)[44-45]现象以及同时性的相对性(relativity of simultaneity)[46-48]. 在爱因斯坦GR[8]中,时空弯曲(curved spacetime)则是最迷人的相对论性效应. 然而,GLT表明,所有这些相对论性现象都只是观测效应.
5.1 关于TD&LC
爱因斯坦SR中,时空呈现时涨尺缩(TD&LC)现象. 假设A和B是O′中同一空间位置(x′B=x′A)发生的2个时间间隔为Δt′=|t′B-t′A|的事件,那么,在O中,相应的时间间隔可能会膨胀:Δt=|tB-tA| =γΔt′>Δt′. 假设L′=|x′B-x′A|是O′中一段空间距离,那么,在O中,相应的空间距离可能会收缩:L=|xB-xA|=γ-1L′ 同样,在GLT下,时空也会呈现TD&LC现象. 根据式(8),如果0 (12) (13) 然而,式(12)(13)显示,TD&LC取决于观测媒介M的速度η:η越高,时空所呈现的TD&LC度越低. 特别地,若η→∞,则Δt=Δt′且L=L′. 可见,没有观测局域性(η=∞),时空不再呈现TD&LC. 爱因斯坦SR中,时空的同时性是相对的:不同的观测者或参考系有不同的同时性. 在O′中同时的事件A和B(|t′B-t′A|=0),可能在O中不同时:若x′B≠x′A,则|tB-tA|=γ|x′B-x′A||v|/c2≠0. 同样,在GLT下,时空的同时性也是相对的. 根据式(8),如果0 |tB-tA|=Γ|x′B-x′A||v|/η2≠0 (x′B≠x′A) (14) 然而,式(14)显示,同时性的相对性也取决于观测媒介M的速度η:η越高,时空所呈现的同时性之相对性越低. 特别地,若η→∞,则当t′B=t′A时tB=tA. 可见,没有观测局域性(η=∞),O和O′将共享绝对的同时性. 根据爱因斯坦GR[8]:物质(质量和能量)的存在导致时空弯曲,而且,物质密度越大,时空的曲率越大. 然而,GLT显示,GR中弯曲的时空,其实,也只是光学观测体系下的一种观测效应,其中,光被隐喻为观测媒介M. 1916年,Schwarzschild[49]得到GR中爱因斯坦场方程第一个精确解. 简单起见,我们通过Schwarzschild度规 (15) 考察弯曲的时空,式中:gμν为静态球对称天体外部弯曲时空的度规;G为万有引力常数;M和r分别为天体质量及其半径. 式(15)中的度规gμν涉及光速c;显然,它源于爱因斯坦ILS假设,隐喻信息传输速度. 在GLT下,用观测信息传播速度η替代光速c,则式(15)中的度规便可推广为 (16) 式(16)显示,借助不同速度的观测媒介,我们将会观测到同一时空之不同的曲率. 特别地,若η→∞,则式(16)蜕化为 (gμν)=diag(-1,1,r2,r2sin2θ) (17) 这恰好就是平直时空的度规,代表伽利略- 牛顿时空. 可见,真实的时空并不是弯曲的. 所谓弯曲时空,只是一种观测效应,恰似我们通过广角镜头所看到的情景. 没有观测局域性(η=∞),时空便会呈现出自己真实而平直的面貌. 伽利略变换和洛伦兹变换,以及GLT,具有相同的形式,只是其时空变换因子(分别为伽利略因子和洛伦兹因子,以及GLT因子)不同而已. GLT因子概括并统一了伽利略因子和洛伦兹因子,表征时空和物质运动的相对论性,是观测局域性(η<∞)在时空变换模型中的体现. 伽利略因子恒等于1,因而,伽利略变换是非相对论性的. 洛伦兹变换γ(v)=1/(1-v2/c2)依赖于相对速度v,给人的印象是,相对论性现象乃物质运动的体现:若|v|>0,则γ(v)>1;|v|越大,则γ(v)越大,相对论性效应因而越显著. 然而,GLT表明,与其说时空变换因子依赖于物质运动(v),不如说它依赖于观测,换句话说,依赖于观测媒介(M)或M的速度(η). 根据式(7),利用泰勒级数,GLT因子可划分为 (18) 式中:Γ∞≡1为伽利略因子(即η→∞时GLT因子的一个特例);ΔΓ(v,η)为Γ(v,η)泰勒级数的其余部分,依赖于η和v,可称作观测效应因子. 自然地,洛伦兹因子γ(v)为GLT因子的另一个特例,可记作Γ(v,c) =Γ∞+ΔΓ(v,c),其中,M为光,η为c. 伽利略因子Γ∞独立于观测,与M及η和v无关,对相对论性效应和观测效应无贡献. 可见,伽利略因子Γ∞表征时空和物质运动的固有属性,是客观世界在物理观测中的真实体现. 显然,无论M是什么,GLT因子Γ(v,η)都包含着代表物理世界真实信息的伽利略因子Γ∞. 作为观测效应,时空和物质运动的相对论性现象由观测效应因子ΔΓ(v,η)表征: (19) 式(19)显示,ΔΓ(v,η)完全依赖于观测:其中的每一项都取决于η和v. 对于一个特定的速度v,不同速度η的观测媒介M导致不同程度的观测效应:η越大,ΔΓ(v,η)越小,相对论性度越低. 特别地,若η→∞(即无观测局域性时),ΔΓ(v,η)→0,所有的相对论性效应都会消失,最终,只剩下伽利略因子Γ∞和真实的物理世界. 可见,相对论性效应并不代表真实的自然现象或物理现实. 相对论性现象的本质是一类观测效应,而根源则在于观测局域性(η<∞). GLT泛化了洛伦兹变换;因而,爱因斯坦SR在GLT的基础上得以概括推广并重新诠释. 根据GLT,相对论性现象乃观测效应,因而,泛化的SR可称为观测相对论(theory of observational relativity, OR). GLT具有与洛伦兹变换完全相同的形式;用观测媒介(M)之速度(η)替代光速(c),爱因斯坦SR中所有的运动学和动力学关系都能被自然而符合逻辑地推广至OR,其中,最基本的关系式当属速度叠加公式(velocity-addition formula)、质速关系(mass-speed relation)、相对论性动量定义(definition of relativistic momentum),以及最为著名的爱因斯坦质能公式(mass-energy equation)E=mc2. 伽利略速度叠加法则由伽利略变换导出,是非相对论性的;爱因斯坦速度叠加法则由洛伦兹变换导出,是相对论性的. 在GLT下,伽利略速度叠加和爱因斯坦速度叠加被统一起来. 对于图3所示的2个惯性观测体系(Σ,M,O)和(Σ,M′,O′),基于式(8)所示的GLT,我们能概括爱因斯坦速度叠加法则,并导出速度叠加的一般关系: (20) 式中:M和M′为相同观测媒介,速度为η;ux、uy、uz分别为Σ在O中沿X、Y、Z轴方向运动的速度,u′x、u′y、u′z分别为Σ在O′中沿X′、Y′、Z′轴方向运动的速度;v为O′相对于O沿X方向运动的速度. 类似于爱因斯坦速度叠加,OR速度叠加也是相对论性的. 然而,式(20)表明,OR速度叠加之相对论性依赖于观测,因而,只是一种观测效应:借助于不同速度η的观测媒介M,同一观测者会因η的不同而形成不同的速度叠加. OR速度叠加法则概括并统一了伽利略速度叠加和爱因斯坦速度叠加. 在波尔对应原理[42-43]下,式(20)中的OR速度叠加法则与爱因斯坦速度叠加和伽利略速度叠加严格对应:若η→c,则式(20)蜕化为爱因斯坦速度叠加;若η→∞,则Γ→1,式(20)蜕化为伽利略速度叠加: (21) 然而,在波尔对应原理下,爱因斯坦速度叠加法则并不能严格地对应伽利略速度叠加法则,而只能在v≪c时近似于伽利略速度叠加. 在牛顿力学中,质量(mass)是物质的固有属性,与物质和观测者的运动状态无关. 然而,在SR中,爱因斯坦引入了相对论性质量(relativistic mass)和静止质量(rest mass)的概念,一个物体的质量依赖于物体的运动速度:m(v)=mo/(1-v2/c2),其中,m和mo分别为物体的相对论性质量和静止质量. 质速关系在爱因斯坦SR中占据着重要的位置. 然而,令人疑惑的是,速度是相对的,依赖于观测者或参考系,因而,在爱因斯坦质速关系下,一个物体的质量和惯性力,乃至其万有引力,都取决于观测或观测者. 对于观测体系(Σ,M,O)和(Σ,M′,O′),假设O′即Oo(如图3所示),那么,Σ静止于O′,u′=0且u=v. 于是,Σ在O中的质量便是其速度为v时的相对论性质量m(v);而Σ在O′中的质量则是其静止质量mo. 基于GLT,爱因斯坦质速关系可推广为更一般的OR质速关系 (22) 其中,m=m(v,η)为Σ在O中的相对论性质量,依赖于观测媒介M的速度η,以及Σ相对于O的速度v. 在OR中,当光担当观测媒介M时,爱因斯坦相对论性质量m(v)可记作:m(v,c). 根据式(22),对于Σ之特定速度v,具有不同速度η的观测媒介M导致Σ不同的相对性质量m(v,η):η越高,则m(v,η)越接近Σ的静止质量mo. 特别地,若η→∞,则 (23) 式中m∞为Σ在牛顿定律下的经典质量. 特别注意,式(23)表明:爱因斯坦SR中的静止质量mo正是牛顿的经典质量m∞. 利用式(18),式(22)可写作 m(v,η)=m∞+Δm(v,η) (24) 式中:m∞=mo为Σ的固有质量,独立于观测,应具有万有引力效应;而Δm(v,η)完全依赖于观测媒介M的速度η,是纯粹的观测效应,而非真实的物质存在. 特别注意,若η→∞,则Δm(v,η)→0;因而,Δm(v,η)不具有万有引力效应. 基于OR质速关系,我们能得出这样的结论:所有的物质粒子,包括光子,都具有自己的静止质量. 光子的静止质量并非为零;根据OR之式(22),我们能从理论上计算出光子静止质量. 物体质量是物体所含物质的量. 只有静止质量才是物质真实的质量和物质真实的存在. 在牛顿力学中,一个物体的动量被定义为经典质量m∞与速度v的乘积:p∞=m∞v,是非相对论性的. 而SR中,爱因斯坦则将其定义为相对论性质量m与速度v的乘积:p=mv=mov/(1-v2/c2),因而,是相对论性的. 对于观测体系(Σ,M,O)和(Σ,M′,O′),假设u′=0且u=v. 那么,Σ在O中的动量便是其速度为v时的相对论性动量;而Σ在O′中的动量自然为零. 基于GLT,因循爱因斯坦SR逻辑,OR将Σ在O中的动量定义为 (25) 自然地,OR之动量也是相对论性的,并且,依赖于观测媒介M的速度η. 根据式(25),对于Σ之特定速度v,具有不同速度η的观测媒介M导致Σ不同的相对性动量p(v,η):η越高,则p(v,η)越接近Σ的经典动量p∞. 特别地,若η→∞,则 (26) 式(26)表明,没有观测局域性(η=∞),OR的相对论性动量p(v,η)便成为牛顿的经典动量p∞. 利用式(18),式(25)可写作 p=p∞+Δp(v,η) (27) 式中,Δp(v,η)完全依赖于观测媒介M的速度η,只代表观测效应,而非真实的运动效应. 特别注意,若η→∞,则Δp(v,η)→0. 物质有2种基本的属性:一是质量(mass),二是能量(energy).E=mc2,即爱因斯坦著名的质能公式,意味着物质的质能和能量是相互依存的:质量是能量,而能量也是质量. 然而,在基于GLT的OR理论中,这种质能相互依存的关系也是一种观测效应. 在E=mc2中,m为物质的相对论性质量,而E则为物质的自由能(free energy),即物质处于自由状态下的能量. 根据爱因斯坦SR,物质的自由能由两部分构成:1)Eo=moc2,即Σ处于静止状态时的自由能;2)K=(γ(v)-1)moc2,即Σ处于运动速度v时的动能. 若v≪c,则爱因斯坦动能K近似于牛顿力学中的经典动能:K≈K∞=m∞v2/2. 对于观测体系(Σ,M,O)和(Σ,M′,O′),假设u′=0且u=v. 那么,Σ在O中的动能便是其速度为v时的相对论性动能;而Σ在O′中的动能为零. 因循爱因斯坦SR逻辑,OR用Σ在O中的相对论性动量p=p(v,η)定义其受力:F=dp/dt. 于是,基于GLT,Σ在O中的相对论性动能为 (28) 自然地,若v=0,则K=0且E=Eo. 令Eo=moη2,那么,根据式(28),可得OR之质能公式 (29) 事实上,由于GLT与洛伦兹变换具有完全相同的形式,用η替代c,可直接地将爱因斯坦质能公式E=mc2变换为OR质能公式E=mη2. 式(29)意味着,E=mc2只是E=mη2的一个特例. 根据式(29),能量E=mη2中包含着观测效应:当同一观测者采用不同M时,同一Σ会展现出不同的自由能. 利用泰勒展开式,Σ在O中的相对论性动能K可划分为两部分: (30) 式中,K∞为牛顿力学之经典动能,与M及其速度η无关;而ΔE(η)中各项依赖于η,因而,只是一种观测效应. 特别值得注意,静态自由能Eo=moη2只是观测效应ΔE(η)的一部分,在牛顿力学中无意义. 根据式(30),若η→∞,则相对论性动能K便成为牛顿力学中的经典动能:K=K∞=m∞v2/2. 或许,式(29)和式(30)所示的OR质能关系,能给予我们对爱因斯坦公式E=mc2以及质量和能量关系新的认识和新的理解. 物理学所有的理论体系或时空模型,既依赖于观测,又制约于观测;其中,观测信息的传播速度扮演着重要角色. 本文基于POL和HOL,从逻辑上和理论上推导出IOMS和GLT,并且,因循爱因斯坦SR逻辑,建立起OR. IOMS定律概括了ILS;于是,ILS假设成为IOMS定律一个特例,仅当光作为观测媒介为观测者传递被观测对象之信息时成立. IOMS定律阐明了光速在迈克尔逊- 莫雷实验中呈现不变性的原因. 根据IOMS,光速并非真地不变或不可超越;迈克尔逊- 莫雷实验中,光既是被观测对象又是观测媒介,因而,其速度看似不变. 可见,迈克尔逊- 莫雷实验并不真地意味着ILS,而恰恰是为IOMS定律提供了一个确切的实证范例. GLT表明,不同观测媒介之观测体系产生不同的理论体系:光学观测体系导致洛伦兹变换和爱因斯坦SR,其中隐喻,传递观测信息的媒介是光;而理想观测体系则导致伽利略变换和牛顿力学,其中隐喻,不存在观测局域性(观测媒介速度无穷大),因而,观测信息的传输不需要时间. 在波尔对应原理[42-43]下,GLT既与伽利略变换严格对应又与洛伦兹变换严格对应. 这种严格的对应关系从一个侧面印证了GLT及其OR理论逻辑上的合理性和理论上的正确性. OR理论表明,所有相对论性效应,本质上都只是一类观测效应,并非真实的自然现象或物理现实,其根源在于观测局域性. 没有观测局域性,时空将呈现其真实的面貌. 可见,真实的物理世界,应该是伽利略和牛顿为我们描述的时空[50-53]:时间和空间相互独立,速度叠加服从伽利略法则,而物质运动则遵循牛顿定律;同时性是绝对的,时间不会膨胀,空间不会收缩,时空更不会弯曲. 或许,现在该是反思人类自然观的时候了. 当然,根据物理观测原理(OPW原理)或POL原理,物理世界不存在速度无穷大的观测媒介. 因而,观测局域性是不可逾越的;相对论性现象和观测效应必定会永远地存在于我们的观测中. OR理论或许能为相对论或物理学提供新的见解:阐明光速为什么会不变和时空为什么会弯曲;诠释电子双缝实验[54-56]中的奇异现象(正如费曼所说,“这不可能,绝对不可能通过任何经典途径加以解释”[57]);理论上确认所有物质粒子皆有其静止质量,给出光子静止质量之理论值;并且,预测超光速物质运动的存在. 根据OR理论,我们没有理由认为光速是宇宙终极速度. 对于物理学和物理学家,探索超光速物质运动或超光速观测媒介,使人类能获得更为即时的观测信息,观测到更为真实的物理世界,无疑是一项意义重大的任务. 需要指出的是,在电子预印本[29-30]中,HOL并非假设或推断,而是由时空和物质运动更基本物理性质导出的逻辑结论. 为了简洁地表达和陈述本文所关注的内容,我们简单而直接地将HOL作为OR理论的逻辑起点. 一个理论体系,应该建立在最基本逻辑前提或第一性原理(first principle)[58-59]之基础上,方能令人不仅知其然而且知其所以然,并且,能将霍金在其《时间简史》[23]中所说的部分理论(partial theory)统一起来. 爱因斯坦SR建立在ILS假设之基础上;而ILS假设并非不证自明,不具有作为逻辑前提或公理的基本特征. 正因为如此,SR无法解释时空和物质运动呈现相对论性效应的原因. OR理论建立在客观世界基本物理属性之基础上[29-30],不仅概括并统一伽利略变换和洛伦兹变换,而且,概括并统一爱因斯坦SR[7]和德布罗意物质波论[17-18],在同一理论体系中导出爱因斯坦公式E=mc2和普朗克方程E=hν,以及德布罗意关系λ=h/p. 本文只是OR理论的一部分. 随后,我们将报告OR理论更多内容和结论. 致谢作者特别感谢国家自然科学基金委员会信息科学部自动化处前处长王成红研究员,他对OR理论做出了富于洞察力的评论;特别感谢北京工业大学严辉教授,他推动了对OR理论研讨. In 1887, following Maxwell’s proposal[1], Michelson and Morley[2]performed an experiment to search for the ether. Without detecting the ether, they encountered into a problem: the Galilean velocity addition law appeared to be invalid. The Michelson-Morley experiment showed that the speed of light plus the orbital speed of the Earth remained at the speed of light. To interpret the Michelson-Morley experiment, FitzGerald proposed the hypothesis that all objects physically contract by a factor of(1-v2/c2) along the line of motion[3]. Later, Lorentz added the hypothesis that time dilates by the factor of 1/(1-v2/c2)[4-6]. Thus, the Lorentz transformation (LT), or the FitzGerald-Lorentz transformation, was conceived. In 1905, Einstein appeared to grasp the key of the Michelson-Morley experiment: the speed of light exhibits no velocity addition effect and is the same for all observers. Subsequently, he proposed the hypothesis of the invariance of the light speed (ILS). Based on the ILS, Einstein theoretically deduced the LT, established the theory of special relativity (SR)[7], and revealed the relativistic phenomena of spacetime and matter motion. The ILS is not only the cornerstone of Einstein’s SR, but also one of the prerequisites of Einstein’s theory of general relativity (GR)[8]. For over a century, Einstein’s theory of relativity including SR and GR has been supported by almost all observations and experiments[9-10]. However, to this day we still do not exactly understand why the speed of light is invariant[11-12]. In addition, we still do not fully understand why spacetime and matter motion exhibit relativistic phenomena[13-14]. The hypothesis of the ILS has one direct corollary: the speed of light is the ultimate speed of the universe, which cannot be exceeded by any form of matter motion. It is worth noting that Einstein integrated this corollary into the principle of locality[15-16]: the speeds of matter motion are not infinite, the speed of light is the upper limit, there is no action at a distance in the universe. In this study, we establish the observability of the physical world (OPW) as a principle or axiom, from which the locality of the physical world (LPW) is logically deduced. However, unlike Einstein’s view of locality the LPW does not imply that the speed of light is the ultimate speed of the universe or that it cannot be exceeded. Rather, it only means that the speeds of matter motion cannot be infinite. The LPW is physical locality, which is an essential attribute of nature. It is worth noting that such physical locality is bound to lead to observational locality: the speed of any observation medium that transmits the information of observed objects must be finite. Naturally observational locality restricts our observations. It is conceivable that the upper limit of speeds that we can observe must not exceed the speeds of observation media. In light of such a heuristic judgement, we propose the hypothesis of the observational limit (HOL). By taking the OPW and the HOL as prerequisites, we logically deduce a significant conclusion: the invariance of observation medium speeds (IOMSs); the ILS is just a special case of the IOMSs and is only valid if light acts as the observation medium. It happens that our observations and experiments mostly employ light or the electromagnetic interaction as medium for transmitting information, which is why our observations and experiments support the ILS as well as SR and GR. However, it is natural that light should not be the only observation medium that can be employed. From the IOMSs, we logically and theoretically deduce the general Lorentz transformation (GLT), which generalizes the LT, and establish the theory of observational relativity (OR), which generalizes Einstein’s SR. The GLT and OR shed light on the essence and root of relativistic phenomena: the speed of light is not truly an invariant that cannot be exceeded; all relativistic effects are observational effects rooted in observational locality rather than real natural phenomena. We always ask what role light plays in the LT and Einstein’s SR, why the speed of light is invariant and cannot be exceeded, why simultaneity in spacetime is relative, why time dilates and space contracts, and why spacetime and matter motion exhibit relativistic phenomena. Without doubt, it is a significant task for physicists to explore and clarify such fundamental problems that Einstein failed to answer. Perhaps the findings and conclusions of this study can provide an insight into Einstein’s theory of relativity and the relativistic phenomena of spacetime and matter motion. Human cognition of the objective world not only depends on observation but is also restricted by observation. All theoretical systems or spacetime models of physics, including the Galilean transformation (GT) and the LT, are linked to our observation means or observation media. That is, all theoretical systems or spacetime models of physics are branded with the marks of observation without exception. Observation is the active acquisition of information from observed objects using our sensory organs or by means of observation instruments. Naturally, observed information must be transmitted from observed objects to our sensory organs or observation instruments in some manner, or by means of certain media, so that we can perceive or detect the observed objects. Accordingly, an observation system can be described as a triple (Σ,M,O) and involves three basic elements: 1) Σ is the observed object, i.e., the emitter of the observed information (OI) or the information of Σ; 2) M is the observation medium, i.e., the transmitter or messenger of the OI; 3) O is the observer, i.e., the receiver of the OI. Note that, in an observation system (Σ,M,O), the most important physical quantity of M is the speed of M, which refers to the speed of M or the OI relative to O when Σ (i.e., the source of the OI) is at rest with respect to O, and is denoted byηin this paper. In four-dimensional (4D) Minkowski spacetime, the motion trace of Σ is a so-calledworldlinedrawn by a sequence of events of Σ. As a point in 4D spacetime, aneventin the worldline contains both spatial information (the location at which it occurs) and temporal information (the instant at which it occurs). These are the most fundamental contents of the OI that O intends to detect. Accordingly, we can call the OI the spacetime information (STI) of Σ. The OI or STI of Σ has to be transmitted to O by means of some type of M. Thus, we ask: What can be employed as M in our observation? It is known that matter exhibits wave-particle duality (WPD), acting as both particles and waves. In the 1920s, de Broglie coined the concept ofmatterwave[17-18]based on WPD. In a broad sense, any form of matter motion is a class of matter waves, such as sound waves, water waves, light waves, electric waves, and even an electron or a piece of rock. Waves have an important physical property:modulability. Hence, waves possess the special capacity to carry and transmit information. In theory, for an observation system (Σ,M,O), any form of matter motion or matter wave can be employed as M to carry and transmit the OI of Σ to O. Light is the most common observation medium, which we take for granted. Because of light, we can see the world using our eyes. However, light is not the only possible M for O’s observation. Suppose that there is a thunderbolt event taking place in the sky as depicted in Fig.1(a); the most basic information of the thunderbolt consists of the location and instant at which it occurs. How can we determine its spacetime coordinate? In any case, we must employ certain observation media to transmit the information of thunderbolt events, so that we can perceive or detect the events. Within human perception, both sound and light can act as the observation media of thunderbolt events. Beyond direct perception, by means of human technology, the radio waves and pulsed magnetic fields emitted by thunderbolts can also function as the messengers of thunderbolt events. Traditional astronomy employs visible light as the observation medium to observe celestial phenomena. Radio astronomy extends the observation medium from visible light to almost the entire radio band, and consequently the cosmic microwave background radiation has been detected[19-20], which is in turn cited as evidence for the Big Bang theory. Currently, the detection of gravitational waves is leading to the concept ofgravitationalwaveastronomy[21-22], in which gravitational interactions rather than electromagnetic interactions are employed as the observation medium. Actually, in physical observation, we can take advantage of all possible M, not merely light. Thus, we ask: What is the difference between different observational media with respect to physical observation or the transmission of OI? As matter waves, different observation media have different speeds. However, no matter what the M is in an observation system (Σ,M,O), its speedηmust not be infinite; hence, there must be a certain observational delay in the transmission of the OI from Σ to O. Sound waves travel at a speed of approximately 343 m/s in the earth’s atmosphere at 20 ℃. When we hear thunder from 10 km away, the OI of the thunderbolt event has already been delayed for nearly 30 s. Although light is significantly faster than sound, lightning can only provide us with delayed OI of thunderbolts. Thunderbolts can be regarded as static observed objects relative to observers; while most observed objects are dynamic. When a bird is flying in the sky, how can we perceive or observe the bird and its movement? We can employ sound as the M to hear the bird using our ears or employ light as the M to observe the bird using our eyes. However, as depicted in Fig.1(b), either sound or light can only provide us with delayed OI or STI of the bird: we hear its chirping, but the bird is no longer at the location where it was chirping, or we see its figure, but that is only where the bird was a moment ago. This isobservationalnon-instantaneity. The observational delay or the so-called observational non-instantaneity of the OI is linked to the speedηof M: the lowerηis, the larger the delay, and the more significant the non-instantaneity. Such a delay or non-instantaneity is bound to restrict our observation and to be reflected in our theoretical systems or models of spacetime. Actually, this has led to the difference between the GT and the LT as well as that between Newtonian mechanics and Einsteinian relativity. It is remarkable that the observational non-instantaneity of the OI is related to the LPW problem and is the embodiment of observational locality, which leads to the observational limit of the speeds of matter motion. Locality, or the principle of locality, plays an important role in modern physics. However, physicists rarely explicitly link the LPW to physical observation. The physical world is observable, and such observability must be a prerequisite for humans to acquire knowledge of nature and to recognize or understand the objective world. Here, the observability of the physical world (OPW) is clearly and explicitly established as a basic principle or an axiom of physics. The principle of the OPW: A physical quantity must be observable; i.e., its observed value must be finite and definite. Notably, the OPW is self-evident, and it is rational to adopt the OPW as a basic principle or axiom; otherwise, we would not be able to recognize and understand the objective world. A physical quantity is a physical property of a phenomenon, body, or substance, and can be quantified through observations or measurements. The mathematical transformations of physical quantities are still physical quantities that still have to obey the principle of the OPW. In theories or mathematical models of physics, physical quantities at singularities are not finite and definite, which according to the OPW cannot be regarded as representing physical reality. Therefore, the OPW can be called thesingularityprinciple. In Hawking’s view[23], physical theories and models break down at singularities. Under the OPW, we can better understand the LPW problem, involving both physical locality and observational locality, and better understand the problem of observational non-instantaneity. Einstein’s view on locality was associated with his hypothesis of the ILS. He believed that there is no action at a distance, and owing to the ILS, an action cannot be faster than the speed of light[15-16]. In 1935, based on locality under the ILS, Einstein, Podolsky, and Rosen (EPR) conceived a famous thought experiment, known as the EPR paradox[24], to query the completeness of quantum mechanics. However, it seems that increasingly more EPR experiments tend to support the existence of quantum entanglement[25-26]. Thus, we wonder if there truly isspookyactionatadistance[27]in the universe. Under the OPW, the LPW is beyond doubt. In fact, the LPW can logically be deduced from the OPW and stated as follows. The principle of physical locality (PPL): Under the OPW, the speeds of matter motion must be finite; thus, there is no action at a distance in the universe. Notably, the PPL is a direct corollary of the principle of the OPW. According to the OPW, the speeds of matter motion are all finite: matter must take time to traverse space. However, unlike Einstein’s view on locality under the ILS, the PPL under the OPW does not imply that the speed of light is the ultimate speed of the universe or that it cannot be exceeded. Rather, it means that there is no such matter motion in the universe with infinite speed. It is noteworthy that physical locality is bound to lead to observational locality and set the upper limit of observed speeds. According to the PPL under the OPW, the speed of an observation medium is finite. Therefore, it takes time for the OI to traverse space. As a corollary, the following principle can be logically deduced from the PPL under the OPW. The principle of observational locality (POL): For an observation system (Σ,M,O), the speedηof M must be finite, i.e.,η<∞, so that the M must take time to transmit the OI from Σ to O. In short, the POL states thatη<∞, which definesabsoluteobservationallocality: regardless of M, there exists observational locality in (Σ,M,O) and an observational delay in the transmission of the OI. The observational locality of an observation system (Σ,M,O), or the finite speedηof M, is bound to restrict O’s observation. Naturally, different M with differentηvalues lead to different degrees of observational delay for the OI, which reflects therelativeobservationallocality: the lower the speedηof M is, the more obvious the observational locality of (Σ,M,O). With experience and intuition, we can make and understand such heuristic judgements: owing to the locality of ultrasonic waves, bats cannot expect to detect supersonic motion by means of ultrasonic waves; owing to the locality of light, humans cannot expect to detect superluminal motion by means of light. By analogy, we establish the following hypothesis. The HOL: For an observation system (Σ,M,O), suppose that O is an inertial observer of Σ then, the speedηof the observation medium M is the upper limit of Σ’s speeduthat O can observe by means of M; i.e., |u|≤η. The HOL suggests that, in an observation system (Σ,M,O), the speedηof M limits the observation range of inertial speeds that O can observe. To break through the observational locality of a specific M, we must employ an observation medium that is faster than the specific M. At present,the mainstream academic view is that the ILS is the embodiment of the light speed being the ultimate speed, which represents objective reality. As Landau et al.[28]remarked: “What is really at stake is the locality of interactions; hence, there exists a theoretical maximal speed of information transmission which must be invariant.” However, the ILS is actually an observational effect resulting from the observational locality of light (η=c<∞). In fact, the Michelson-Morley experiment does not imply the ILS, but it does demonstrate a significant phenomenon in physical observation: the speeds of observation media are observationally invariant for observers. This phenomenon can be derived from the POL and the HOL and is stated as a law as below. The law of the IOMSs: The speeds of observation media are observationally invariant, i.e., the same for all inertial observers, regardless of the motion of observers and observed objects. More formally, the law of the IOMSs can be stated: Let (Σ,M,O) and (Σ,M′,O′) be Σ’s two inertial observation systems, where Σ moves at speeds ofuin O andu′ in O′, respectively, and O′ moves relative to O at an inertial speed ofvor O′ moves relative to O at an inertial speed of -v. Suppose that M and M′ are the same observation medium; then, its speedηis observationally invariant, i.e., the same relative to O and O′. The IOMSs means that the speeds of observation media have no velocity addition effect: the speedηof M plus any inertial speed remainsη. Proof. In addition to the POL and the HOL, we need to take the principle of relativity as a prerequisite of the IOMSs and suppose that the relative speed |v| between O and O′ is lower than the speedηof M, i.e., |v|<η. The relative motion among Σ and the M as well as O in (Σ,M,O) and O′ in (Σ,M,O′) is depicted in Fig.2. According to the basic physical properties of matter motion, there must be certain superposition relationships among the inertial speedsu,u′ andv: the speeduof Σ observed by O should be the superposition of the speedu′ of Σ observed by O′ and the speedvof O′ relative to O (u=u′⊕v), whileu′ should be the superposition ofuand the speed -vof O relative to O′ (u′=u⊕(-v)). Then we define the velocity addition operator “⊕”: (1) which obeys the basic physical properties of matter motion and the basic laws of mathematical operations. Under the principle of relativity, with the same observation medium(M=M′), the observation systems (Σ,M,O) and (Σ,M′,O′) have symmetry in the observed spacetimes and equivalence with respect to the formulation of physical laws. That is, O and O′ are equal in status, and physical laws are invariant and have the same form in O and O′. Therefore, the following inverse operation holds for the velocity-addition operator “⊕”: ifu=u′⊕vthenu′=u⊕(-v) (2) According to the POL,η<∞; then we can suppose that |u′|=η. With Eq.(1), whenu′ andvare in the same direction, we have |u|=|u′⊕v|=|u′|⊕|v|=η⊕|v| (3) Thus,we obtain |u|≥ηfrom Eqs. (1) and (3) and |u|≤ηfrom the HOL. Hence |u|=η, and Eq. (3) can be rewritten asη=η⊕|v|, which according to Eq. (2) impliesη=η⊕(-|v|) if |v|<η. Then we have ∀v∈(-η,η),η⊕v=η (4) which suggests that the speedηof M has no velocity addition effect in an inertial spacetime and is invariant or the same relative to O and O′. Thus, the IOMSs holds under the POL and HOL. □ The law of the IOMSs is a logical consequence of the HOL. In this paper, the HOL is only a hypothesis or heuristic judgement. However, in the e-preprints [29-30], both the IOMSs and HOL are logical conclusions derived from more basic physical properties of spacetime and matter motion. Under the IOMSs, we can better understand the ILS and relativistic effects. The IOMSs has profound implications. Let us start with some basic problems or concerns about the IOMSs and the ILS. What new insight can the IOMSs provide into the ILS? The IOMSs generalizes the ILS. Now, the ILS is no longer a hypothesis but rather a corollary or special case of the IOMSs and can be expressed as below. The ILS under the IOMSs: The speed of light is observationally invariant or the same for all inertial observers if and only if light acts as the observation medium that transmits the OI from observed objects to observers. Notably, the speed of light in the above ILS is the speed at which light propagates in observed spacetime, not necessarilyc(=299 792 458 m/s), unless the observed spacetime is simply vacuum. That is, Einstein’s ILS hypothesis can only be valid if light acts as the observation medium and the observed spacetime is vacuum. Why is light seemingly invariant in the Michelson-Morley experiment? Are the ILS and the IOMSs real natural phenomena? The IOMSs has revealed the nature of the ILS. In the Michelson-Morley experiment[2], light acted as both the Σ and the M, so the speed of light “looked” as if it was invariant at that moment. The same is true for other observations and experiments on the ILS, such as the phenomenon of stellar aberration[31-32]and the Kennedy-Thorndike experiment[33]. In fact, the speed of light is not truly invariant. The IOMSs suggests that all matter motion or matter waves, not just light, can be employed as observation media. Different matter waves have different speeds; however, under the IOMSs, the speed of any matter wave will exhibit observational invariance for observers so long as it acts as observation medium. It is thus clear that the IOMSs, including its special case of the ILS, is simply an observational effect rather than a real natural phenomenon or physical reality. Notably, the ILS is the prerequisite of Einstein’s SR, which perhaps implies that all relativistic phenomena in SR, and even in GR, are observational effects. Under the IOMSs, what are invariant speeds? Is an invariant speed the ultimate speed of the universe? The so-calledinvariantspeedrefers to a speed that is measured to be the same by all inertial observers. So far, physicists generally deem that the invariant speed must be the ultimate speed limit of the universe, and owing to the ILS, it must be the speed of light. However, the IOMSs suggests that different observation systems have different invariant speeds: Newtonian mechanics implies that the transmission of information takes no time and the invariant speed is thus infinite; Einstein’s SR implies that light or the electromagnetic interaction is the messenger of information and the invariant speed is thus the speed of light. However, in bats’ echolocation system, ultrasound acts as the observation medium, and the invariant speed is thus the speed of the ultrasonic wave. It is thus clear that such seemingly invariant speeds cannot represent the ultimate speed of the universe, but rather represent an observational effect. Under the IOMSs, in the physical world, there is no truly invariant speed; therefore, there is no so-called ultimate speed. It is worth noting that, the terminvariantspeedhas different implications for the ILS and the IOMSs. In the ILS and Einstein’ SR, the invariant speed is compulsively defined withc(=299 792 458 m/s), i.e., the speed of light in vacuum, regardless of the motion of light sources and inertial observers. Under the IOMSs, the invariant speed in an observation system (Σ,M,O) is defined as the speed of M relative to O when Σ (i.e., the source of the OI) is at rest with respect to O. Therefore, for an optical observation system where light acts as M, the invariant speed is the speed of light relative to O when the light source is at rest with respect to O rather thancunless O’s observed spacetime is vacuum. What new insight can the IOMSs provide into the principle of relativity? The principle of relativity[7,34]implies that inertial spacetime is symmetric, all inertial observers or inertial frames of reference are equal in status, and therefore the laws of physics have the same form in all inertial frames. Einstein generalized this principle to non-inertial frames, i.e., the so-calledgeneralprincipleofrelativity[8,34]: all systems of reference are equivalent with respect to the formulation of the fundamental laws of physics. The real objective spacetime might or should be symmetric; however, under the IOMSs, the observed spacetime cannot necessarily be symmetric. Restricted by observations or by observation media, spacetime in our eyes can only be the observed spacetime rather than the objective spacetime. Under the IOMSs, the symmetry of the observed spacetime depends on whether the observers or observation systems employ the same observation medium, not on if the reference frames are inertial. The IOMSs suggests that two observation systems (Σ,M,O) and (Σ,M′,O′) are symmetric and equivalent with respect to the formulation of physical laws or observers O and O′ are equal in status in the observed spacetime, only if the observation media M and M′ are the same. It follows that the principle of relativity we take it for granted is conditional: it can only be valid if observers observe the objective world by means of the same observation medium. Is there any observational or experimental evidence for the IOMSs, and how can the IOMSs be verified by experiments? To a large extent, physics is an empirical science; ultimately, the correctness or validity of a physical law must be examined by observations and experiments rather than theory. The ILS is the cornerstone of Einstein’s SR, but SR cannot explain why the speed of light is invariant. Physicists believe the ILS because the speed of light exhibits invariance in our observations and experiments. Actually, such observations and experiments, including the Bradley observation[31]and the Michelson-Morley experiment[2], do not provide as much empirical evidence for the ILS as for the IOMSs, in which light or the electromagnetic interaction takes on the role of the observation medium; thus, the ILS is just a specific embodiment of the IOMSs. Perhaps, under the IOMSs, we can design experiments to test the invariance of the speeds of subluminal media (for example, electrons or electronic waves) or even superluminal media (for example, gravitons or gravitational waves). The LT is a spacetime transformation model in which light is implied as the M and the transmission speedηof the OI is implied asc, i.e., the speed of light in vacuum. However, it is noteworthy that in an observation system (Σ,M,O) the M does not have to be light andηdoes not have to bec. Now that the ILS has been generalized as the IOMSs, the LT based on the ILS can naturally be generalized to any M or anyη. It is recognized that relativistic effects do not have to depend on the physical properties of light. It is generally accepted in the mainstream view that relativistic effects depend on the LPW and the symmetry of spacetime[35]. Therefore, without the ILS, the LT and Einstein’s SR can also be deduced from locality and symmetry[36-37]. With the symmetry and isometry of spacetime, the LT has been mathematically generalized as the Lorentz group[38]and even as the Poincare group[39]. Group theory generalizes the Lorentz factorγ=1/(1+v2/c2) asΓ=1/(1+κv2). However, under the group axioms,κhas no exact physical significance, but represents three possible cases: 1)κ>0, which does not agree with physical reality; 2)κ=0 andΓ=1, which is non-relativistic and does not agree with Einstein’s SR; 3)κ<0 andΓ>1, which is relativistic and an alternative to SR as long asκcan be determined. According to the mainstream view, owing to physical locality spacetime must involve a negativeκ(case 3):κ=-1/Λ2<0, whereΛis assumed to be a definite cosmological constant denoting the ultimate speed of the universe, and needs to be determined through an experiment. With the ILS,Λ=c. As Landau et al.[28]remarked: “It turns out that this speed coincides with the speed of light in vacuum.” In the above inference, it a serious mistake to regard the maximum speed as aninvariantspeed. In fact, according to the IOMS, there exists no so-calledinvariantspeedorultimatespeedin the universe. We can draw the following conclusions from the locality of spacetime: 1) the speeds of all forms of matter motion are limited; 2) in which there must be one having the maximum speed. However, the maximum speed is by no means aninvariantspeed. Landau and Lifshitz realized thatcin the Lorentz factor represents the speed of information transmission[28]. However, physicists do not seriously reflect on whether the M can be different from light, or whether the speed of information transmission can be different fromc. Under the IOMSs, by directly substitutingηforcone can generalize the LT to thegeneralLorentztransformation(GLT). However, to better understand the physical significance of the GLT, we follow Einstein’s logic way in SR[7]to deduce the GLT from the IOMSs instead of the ILS. Similar to the LT, the GLT is also a relativistic transformation model of spacetime. Relativistic effects imply that space and time are interdependent and indivisible. Therefore, space and time are merged intospacetime. Different reference frames represent different spacetimes. In Fig.3, (Σ,M,O) and (Σ,M′,O′) can be regarded as two different inertial spacetimes of the observed object Σ. The transformations between them are denoted as O′→O and O→O′. Naturally, the transformations between (Σ,M,O) and (Σ,M′,O′) are conditional. The transform requirement for observed spacetimes: For inertial observation systems (Σ,M,O) and (Σ,M′,O′), the observed spacetimes of O and O′ can be transformed between each other if and only if M and M′ are the same observation medium, so that O and O′ are equal in status, and the observed spacetimes are symmetric. The logical prerequisites for the GLT: The first is the principle of simplicity; The second is the principle of relativity; The third is the law of the IOMSs (instead of Einstein’s ILS). As depicted in Fig.3, we define a free 3D Cartesian coordinate frame Ootaking Σ as its origin. Naturally, Oois an intrinsic inertial frame of Σ, by which any inertial frame of Σ, such as O and O′, can be defined. Suppose there are no relative movements between O and O′ in the directions ofY(orY′) andZ(orZ′); then,Y=Y′ andZ=Z′, and we need to examine only the relative movement between O and O′ in the directions ofX(orX′). Without loss of generality, suppose that: as depicted in Fig.3(a), att=t′=0, Σ, O and O′ coincide; as depicted in Fig.3(b), att>0 andt′>0, Σ moves at a speed ofualongXin O and at a speed ofu′ alongX′ in O′, and O′ moves at a speed ofvalongXrelative to O or O moves at a speed of -valongX′ relative to O′. Following Einstein’s logic way in SR, we divide the deduction of the GLT into three sections as below. The first is based on the principle of simplicity. In fact, Einstein’ SR[7]has one more prerequisite other than the principle of relativity and the hypothesis of the ILS, that is, the principle of simplicity[40-41], under which O′→O can be supposed to take a linear form: x=Γx′+bt′ (5) Einstein attributed such linear relationship to the homogeneity of spacetime[7]: “In the first place it is clear that the equations must be linear on account of the properties of homogeneity which we attribute to space and time.” The basic relationship between space and time demands thatx′=-vt′ ifx=0, and sob=Γv. Thus, Eq. (5) can be further simplified asx=Γ(x′+vt′). The second is based on the principle of relativity. If the observation media M and M′ are the same, according to the principle of relativity, (Σ,M,O) and (Σ,M′,O′) are symmetric; thus, O→O′ should take the same form as O′→O:x′=Γ(x-vt′). By combiningx=Γ(x′+vt′) andx′=Γ(x-vt′), then we have thatt=Γ(t′+(1-Γ-2)x′/v) andt′=Γ(t-(1-Γ-2)x/v). Under the definitions of the speeds of Σ in O and O′, it follows that (6) The third is based on the law of the IOMSs. Suppose that the speed of M isη. Under the law of the IOMSs,u=ηifu′=η. Then, from Eq. (6), we obtain the transformation factor of spacetime of the GLT (theGLTfactorfor short): (7) whereηhas clear and explicit physical significance, representing the speed at which the M transmits the OI of Σ. It is worth noting thatηdepends on the M that is employed by O and O′, is not a definite cosmological constant, and does not have to bec. Now, in summary, we obtain the GLT as follows: (8) The GLT formulated by Eq. (8) generalizes the LT, which has exactly the same form as the LT; therefore, Einstein’s SR on the basis of the LT can logically be generalized on the basis of the GLT. The GT and the LT are two important spacetime transformations in physics. Undoubtably, it is of great significance for physics to unify the GT and the LT. In the LT, light acts as a messenger to transmit the OI. However, in the GLT, light is not the only possible observation medium. In theory, any form of matter motion or matter waves, such as sound waves, electron flows, pulsed magnetic fields, gravitational waves, or even an observed object itself, can be employed as observation media. The GLT suggests that different observation systems lead to different spacetime transformations. The GT is a product of the idealized observation system (η→∞), in which the speedηof M is implied to be infinite and so there is no observational locality in the GT. The LT is a product of the optical observation system, in which the M is implied to be light or the electromagnetic interaction andηis implied to bec. Now, the GLT generalizes and unifies the GT and the LT. Under Bohr’s correspondence principle[42-43], the GLT strictly corresponds to the GT: the GLT reduces to the GT asη→∞ (9) meanwhile, strictly corresponds to the LT: the GLT reduces to the LT asη→c (10) Notably, the mainstream view deems that the LT corresponds to the GT under Bohr’s correspondence principle[42-43]. In fact, the LT cannot strictly correspond to the GT. The LT can only approximate the GT ifv≪c: (11) The strict correspondence of the GLT to the GT and the GLT to the LT reflects the logical rationality and theoretical validity of the GLT from one aspect. The IOMSs reveals why the speed of light is invariant in the Michelson-Morley experiment, while the GLT reveals why spacetime and matter motion exhibit relativistic phenomena. Einstein believed that the objective world is essentially relativistic. However, the GLT suggests that relativistic phenomena are just a class of observational effects that depend on observation, and are restricted by the speeds of observation media. In Einstein’s SR[7],timedilationandlengthcontraction(TD&LC)[44-45]and therelativityofsimultaneity[46-48]are the most well-known relativistic effects. In Einstein’s GR[8],curvedspacetimeis the most fascinating relativistic effect. However, the GLT suggests that these are all observational effects. In Einstein’s SR, spacetime exhibits TD&LC. IfAandBare two events in O′ at the same spatial location (x′B=x′A) with the time interval Δt′=|t′B-t′A|, then the time interval in O is Δt=|tB-tA|=γΔt′>Δt′. IfL′=|x′B-x′A| is a spatial distance measured in O′, then correspondingly in O,L=|xB-xA|=γ-1L′ Similarly, spacetime under the GLT also exhibits TD&LC. From Eq. (8), if 0 (12) (13) However, Eqs. (12) and (13) show that TD&LC depend on the speedηof M. The higherηis, the less obvious the TD&LC exhibited by spacetime. In particular, ifη→∞, then Δt=Δt′ andL=L′. It follows that, without observational locality (η=∞), spacetime would no longer exhibit TD&LC. In Einstein’s SR, the simultaneity of spacetime is relative: different observers or reference frames have different simultaneities. The simultaneous eventsAandB(|t′B-t′A|=0) in O′ may not be simultaneous in O: ifx′B≠x′Athen |tB-tA|=γ|x′B-x′A||v|/c2≠0. Similarly, simultaneity under the GLT is also relative. From Eq. (8), if 0 |tB-tA|=Γ|x′B-x′A||v|/η2≠0 (x′B≠x′A) (14) However, Eq. (14) shows that the relativity of simultaneity depends on the speedηof M. The higherηis, the less obvious the relativity of simultaneity exhibited by spacetime. In particular, ifη→∞, thentB=tAwhent′B=t′A. It follows that,without observational locality (η=∞), O and O′ would share absolute simultaneity. According to Einstein’s GR[8], spacetime is curved due to the existence of matter (mass and energy); the higher the density of matter, the larger the curvature of spacetime. However, the GLT suggests that GR’s curved spacetime is also only an observational effect in the optical observation system where light is implied to be the observation medium M. In 1916, Schwarzschild[49]provided the first exact solution to Einstein’s field equations of GR. For simplicity, we examine curved spacetime through the Schwarzschild metric (15) wheregμνis the metric of curved spacetime outside a static spherically symmetric celestial body;Gis the gravitational constant; andMandrare the mass and radius of the celestial body, respectively. The metricgμνin Eq. (15) involves the light speedcthat of course comes from Einstein’s ILS. Under the GLT, by replacing the light speedcwith the transmission speedηof the OI, the metricgμνin Eq. (15) can be generalized as (16) Eq. (16) shows that, by means of different observation media with different speeds, we will observe different curvatures of the identical spacetime. In particular, asη→∞, Eq. (16) reduces to (gμν)=diag(-1,1,r2,r2sin2θ) (17) which is simply the metric of flat spacetime, representing Galileo-Newton spacetime. It is thus clear that real spacetime is not curved. The so-called curved spacetime is an observational effect,similar to what we see through a wide-angle lens. Without observational locality (η=∞), spacetime would exhibit its real nature. The GT, LT, and GLT have the same form but different spacetime transformation factors, the Galilean, Lorentz, and GLT factors, respectively. The GLT factor generalizes and unifies the Galilean factor and the Lorentz factor, which characterizes the relativistic effects of spacetime and matter motion, and is the embodiment of observational locality (η<∞). The Galilean factor is identically equal to 1; hence, the GT is non-relativistic. The Lorentz factor isγ(v)=1/(1-v2/c2), which depends on the relative speedvand gives the impression that relativistic phenomena are the embodiment of matter motion:γ(v)>1 if |v|>0; when |v| is higher,γ(v) is larger, and the relativistic effects are more significant. However, the GLT suggests that the spacetime transformation factor does not depends onmatter motion as much as on observation, in other words, on the M or the speedηof M. According to Eq.(7), the GLT factorΓ(v,η) can be divided into two parts by the Taylor expansion: (18) whereΓ∞≡1 denotes the Galilean factor and is a special case of the GLT factor ifη→∞ and ΔΓ(v,η), the rest of the series, can be calledtheobservation-effectfactorowing to its dependence onηandv. Naturally, the Lorentz factorγ(v) is another special case of the GLT factor and can be denoted asΓ(v,c)=Γ∞+ΔΓ(v,c), where the M is light andηisc. The Galilean factorΓ∞is independent of observation, regardless of M,ηandv, and does not contribute to relativistic effects and observational effects. It follows that the Galilean factorΓ∞characterizes the inherent attributes of spacetime and matter motion and is the true embodiment of the objective world in physical observation. Notably, regardless of M,Γ(v,η) contains the Galilean factorΓ∞that represents the truth of the physical world. As observational effects, the relativistic phenomena of spacetime and matter motion are characterized by the observation effect factor ΔΓ(v,η): (19) Eq. (19) shows that ΔΓ(v,η) totally depends on observation: every item is dependent onηandv. For a specificv, different M with differentηvalues lead to different degrees of relativistic effects: whenηis higher, ΔΓ(v,η) is smaller, and the relativistic degrees are lower. In particular, ifη→∞ (i.e., without observational locality), then ΔΓ(v,η)→0, and all relativistic effects would completely disappear from our observation; only the Galilean factorΓ∞and the objective world would remain. It is thus clear that relativistic effects do not represent real natural phenomena or physical reality: the essence is a class of observational effects, and the root lies in observational locality (η<∞). The GLT generalizes the LT so that Einstein’s SR will be generalized and reinterpreted on the basis of the GLT. According to the GLT, relativistic phenomena correspond to observational effects; thus, SR generalized by the GLT can be called the theory ofobservationalrelativity(OR). The GLT has exactly the same form as the LT. Therefore, by substituting the speedηof M for the light speedcof light, all the kinematic and dynamic relations in Einstein’s SR can logically be generalized to OR, in which the most basic relations involve the velocity addition formula, the mass-speed relation, the definition of relativistic momentum, and Einstein’s famous mass-energy equationE=mc2. Galileo’s velocity addition law is non-relativistic and derived from the GT. Einstein’s velocity addition law in SR is relativistic, and derived from the LT. Under the GLT, Galileo’s velocity addition and Einstein’s velocity addition laws are unified. For two inertial observation systems (Σ,M,O) and (Σ,M′,O′) as depicted in Fig. 3, suppose that M and M′ are the same observation medium with speedη;ux,uy, anduzare the speeds of Σ in O along theX,Y, andZaxes, respectively;u′x,u′y, andu′zare the speeds in O′ along theX′,Y′, andZ′ axes; andvis the speed of O′ relative to O alongX. Then, with the GLT of Eq. (8), we can generalize Einstein’s velocity addition law and derive the general relationship of velocity addition in OR: (20) Similar to Einstein’s velocity addition law, the velocity addition law of OR in Eq. (20) is also relativistic. However, Eq. (20) suggests that the relativistic effect of velocity addition in OR depends on observation and thus is just an observational effect: by means of different M with differentηvalues, an identical observer has different velocity addition laws. The velocity addition law of OR generalizes and unifies Galileo’s velocity addition and Einstein’s velocity addition laws. Under Bohr’s correspondence principle[42-43], the velocity addition law of OR in Eq. (20) strictly corresponds to Einstein’s velocity addition law and Galileo’s velocity addition law: ifη→c, then Eq. (20) reduces to Einstein’s velocity-addition formula; ifη→∞, thenΓ→1 and Eq. (20) reduces to Galileo’s velocity addition formula: (21) However, Einstein’s velocity addition law cannot strictly correspond to Galileo’s velocity addition law but can only approximateit whenv≪c. In Newtonian mechanics, mass is the intrinsic attribute of matter, regardless of the motion states of matter and observers. However, in SR, Einstein introduced the concepts ofrelativisticmassandrestmass; and thus, the mass of a body depends on its moving speed:m(v)=mo/(1-v2/c2) wheremandmoare the relativistic mass and rest mass, respectively. The mass-speed relation occupies an important position in Einstein’s SR. However, it is very puzzling that the speed of a body is relative and depends on observers or reference frames; thus, under Einstein’s mass-speed relation, the mass, inertial force and even gravitational force would depend on observation or observers. For (Σ,M,O) and (Σ,M′,O′), suppose that O′ is Oo(depicted in Fig.3); then, Σ is at rest in O′,u′=0 andu=v. Thus, the mass of Σ in O will be its relativistic massm(v) at the speedv, while that in O′ will be its rest massmo. Under the GLT, Einstein’s mass-speed relation in SR can be generalized by OR as (22) wherem=m(v,η) is the relativistic mass of Σ in O, depending on both the speedηof M and the speedvof Σ relative to O. In OR, when light acts as M, Einstein’s relativistic massm(v) is denoted asm(v,c). According to Eq. (22), at a specific speedv, different M with differentηleads to differentm(v,η): whenηis higher,m(v,η) is closer tomo. In particular, ifη→∞, then (23) wherem∞is the classical mass of Σ under Newton’s laws. Notably, Eq. (23) suggests that the rest massmoin Einstein’s SR is just Newton’s classical massm∞. Using Eq.(18), Eq.(22) can be written as m(v,η)=m∞+Δm(v,η) (24) wherem∞=mois the inherent mass of Σ that is independent of observation and has gravitational effects, while Δm(v,η) totally depends on the speedηof M, and completely represents observational effects rather than the real existence of matter. Notably, Δm(v,η)→0 ifη→∞; thus, Δm(v,η) has no gravitational effect. According to the mass-speed relation of OR, we can conclude that all matter particles, including photons, have their own rest masses. Photons are not massless; with Eq. (22) of OR, we can calculate the theoretical value of the rest mass of a photon. The mass of an object is the amount of matter contained in the object. Only the rest mass is the real mass of matter and represents the real existence of matter. In Newtonian mechanics, the momentum of a body is defined asthe product of its classical massm∞and its speedv:p∞=m∞v, which is non-relativistic. In SR, Einstein defined the momentum of a body as the product of its relativistic massmand its speedv:p=mv=mov/(1-v2/c2), which is relativistic. For (Σ,M,O) and (Σ,M′,O′), suppose thatu′=0 andu=v; then, the momentum of Σ in O will be the relativistic momentum at the speedv, while the momentum in O′ will be zero. Under the GLT, following Einstein’s logic way in SR, OR defines the momentum of Σ in O as (25) Naturally, the momentump=p(v,η) in OR is also relativistic, and depends on the speedηof M. For a specificv, different M with differentηvalues lead to differentp(v,η): whenηis higher,p(v,η) is closer to the classical momentump∞. In particular, ifη→∞, then (26) which suggests that without observational locality (η=∞), the relativistic momentump(v,η) in OR is just the classical momentump∞under Newton’s laws. Using Eq. (18), Eq. (25) can be written as p=p∞+Δp(v,η) (27) where Δp(v,η) totally depends on the speedηof M, and only represents observational effect, rather than real motion effect. Notably, Δp(v,η)→0 ifη→∞. Matter has two essential attributes: mass and energy.E=mc2, Einstein’s famous mass-energy relation, suggests that mass and energy are interdependent: mass is energy, and energy is mass. However, in OR under the GLT, this interdependence of mass and energy is also an observational effect. InE=mc2,mis the relativistic mass of matter, whileEis the free energy of matter, i.e., the energy of matter in the free state. According to Einstein’s SR, the free energyEof matter consists of two parts: 1)Eo=moc2, the free energy of Σ at rest, and 2)K=(γ(v)-1)moc2, the relativistic kinetic energy of Σ at speedv. Ifv≪c, then Einstein’s kinetic energyKis approximately the classical kinetic energyK∞in Newtonian mechanics:K≈K∞=m∞v2/2. For (Σ,M,O) and (Σ,M′,O′), suppose thatu′=0 andu=v; then, the kinetic energy of Σ in O will be the relativistic kinetic energy at the speedv, while the kinetic energy in O′ will be zero. Following Einstein’s logic way in SR, OR defines the forceFon Σ with its momentump=p(v,η) in O asF=dp/dt; then, under the GLT, the relativistic kinetic energy of Σ in O is (28) Naturally, ifv=0 thenK=0 andE=Eo. LetEo=moη2; then, from Eq. (28), we have the mass-energy equation of OR under the GLT: (29) In fact, as the GLT has exactly the same form as the LT, the Einstein formulaE=mc2can be directly generalized asE=mη2by replacing the light speedcwith the speedηof M. Eq.(29) suggests thatE=mc2is only a special case ofE=mη2. According to Eq.(29), the energyE=mη2contains observational effects: for an identical observer with different M, an identical Σ exhibits different free energies. Through the Taylor expansion, the relativistic free energyKof Σ in O can be de divided into two parts: (30) whereK∞is the classical kinetic energy under Newton’s laws, regardless of M andη, while each item in ΔE(η) depends onηand thus only represents an observational effect. It is worth noting that, the rest energyEo=moη2is just part of ΔE(η), and has no significance in Newtonian mechanics. According to Eq. (30), ifη→∞, then the relativistic kineticKwill exactly be the classical kinetic energy:K=K∞=m∞v2/2. Perhaps, OR’s mass-energy relations in Eqs. (29) and (30) can provide a new understanding of the Einstein formulaE=mc2and the relationship between mass and energy. All theoretical systems or spacetime models of physics not only depend on observation, but are also restricted by observation, in which the transmission speeds of the OI play important roles. In this study, on the basis of the POL and the HOL, we have logically deduced the IOMSs, theoretically derived the GLT, and following Einstein’s logic way in SR, established the theory of OR. The law of the IOMSs generalizes the ILS, so that the ILS becomes a special case of the IOMSs, and is only valid if light acts as the observation medium to transmit the OI from observed objects to observers. The IOMSs elucidates why the speed of light exhibited invariance in the Michelson-Morley experiment. Under the IOMSs, the speed of light is not truly an invariant that cannot be exceeded. In the Michelson-Morley experiment, light acted as both the observed object and the observation medium; thus, the speed of light appeared as if it was invariant at that moment. It follows that the Michelson-Morley experiment does not truly imply the ILS, but rather provides an exact empirical example for the IOMSs. The GLT suggests that different observation systems with different observation media produce different theoretical systems: the optical observation system leads to the LT and Einstein’s SR, where light is implied to be the observation medium; the idealized observation system leads to the GT and Newton’s theory, where there is no observational locality (the speed of the observation medium is implied to be infinite); thus, the transmission of the OI requires no time. Under Bohr’s correspondence principle[42-43], the GLT strictly corresponds to both the GT and the LT. Such strict correspondence, from one aspect, corroborates the logical rationality and theoretical validity of the GLT and the theory of OR. The theory of OR suggests that all relativistic effects are essentially a class of observational effects, rather than real natural phenomena and physical reality, and have their root in observational locality. Without observational locality, spacetime would present its real nature. Therefore, the real physical world should be the spacetime described by Galileo and Newton[50-53]: space and time are independent of each other, velocity addition follows Galileo’s law, and matter motion follows Newton’s laws; simultaneity is absolute, time does not dilate, space does not contract, and spacetime does not bend. Perhaps it is time to reflect on human beings’ view on nature. Of course, according to the principle of the OPW or the POL, there is no observation medium with an infinite speed in the physical world. Therefore, observational locality is insurmountable, and the relativistic phenomena of spacetime and matter motion must always reside in our observations. The theory of OR provides new insight into relativity and physics: elucidating why the speed of light would be invariant and why spacetime would bend; interpreting the strange phenomena in double-slit experiments[54-56]“which is impossible, absolutely impossible, to explain in any classical way”, as Feynman claimed[57]; confirming theoretically that all matter particles have their own rest masses and giving the theoretical values of the rest masses of photons; and predicting the existence of superluminal matter motion. In light of OR, we have no reason to suppose that the speed of light is the ultimate speed of the universe. It is a significant task for physicists to probe superluminal motion and superluminal media (for example, gravitons) so that we can obtain more instantaneous OI and observe a more real physical world. It should be noted that in the e-preprints [29-30], the HOL is not a hypothesis or speculation but a logical consequence derived from more basic physical properties of spacetime and matter motion. For the sake of a concise presentation of the concerns of this paper, we simply take the HOL as the logical start of the theory of OR. A theoretical system should be built on the most-basic logical prerequisites orfirstprinciples[58-59], so that it allows us to not only know what and how but also know why and so that it can unify what Hawking calledpartialtheoriesin his bookABriefHistoryofTime[23]. Einstein’s SR is based on the hypothesis of the ILS that is not self-evident and has no the basic feature as a logical presupposition or axiom. As a result, SR fails to explain why spacetime and matter motion would exhibit relativistic phenomena. The theory of OR is based on the basic physical properties of the objective world[29-30]; not only generalizes and unifies the GT and the LT, but also generalizes and unifies Einstein’s SR[7]and de Broglie’s theory of matter waves[17-18]; and theoretically derives Einstein’s formulaE=mc2, Plank’s equationE=hνand the de Broglie relationλ=h/pfrom the same theoretical system. This paper is just part of the theory of OR. Subsequently, we will report more outcomes of OR. Acknowledgements: The author is particularly grateful to Chenghong WANG, a former official at the National Natural Science Foundation of China, for his insightful comments on the theory of observational relativity (OR), and to Hui YAN, a professor at Beijing University of Technology, for his efforts to promote the discussion on the theory of OR.5.2 关于同时性的相对性
5.3 关于时空弯曲

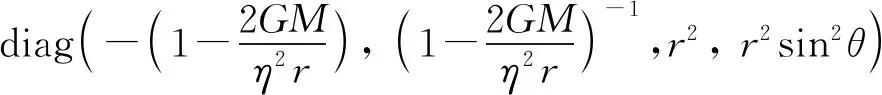
5.4 关于时空变换因子

6 观测相对论
6.1 速度叠加公式
6.2 质速关系
(m∞=Γ∞mo=mo; Δm(v,η)=ΔΓ(v,η)mo)6.3 动量之定义
(p∞=m∞v, Δp(v,η)=ΔΓ(v,η)mov)6.4 质能公式


7 结束语
1 Observation and Media
1.1 Basic Elements in Observation
1.2 Observation Media
1.3 Observational Non-instantaneity
2 Observation and Locality
2.1 Observability
2.2 Locality under the OPW
2.3 Observational Locality
2.4 Hypothesis of the Observational Limit (HOL)
3 Invariance of Observation Medium Speeds
3.1 Deduction from the HOL

3.2 Implication of the IOMSs
4 General Lorentz Transformation
4.1 The ILS and LT
4.2 The IOMSs and GLT
4.3 Unification of Spacetime Transformations
5 The Essence and Root of Relativistic Effects
5.1 On TD&LC
5.2 On the Relativity of Simultaneity
5.3 On Curved Spacetime

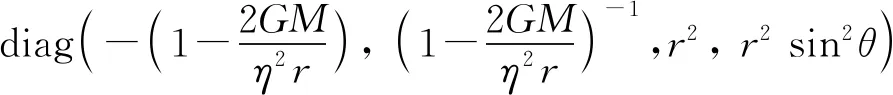
5.4 Spacetime Transformation Factors

6 Observational Relativity
6.1 Velocity Addition Formula
6.2 Mass-Speed Relation
(m∞=Γ∞mo=mo; Δm(v,η)=ΔΓ(v,η)mo)6.3 Definition of Momentum
(p∞=m∞vand Δp(v,η)=ΔΓ(v,η)mov)6.4 Mass-Energy Equation


7 Conclusion

