基于投入协同演化视角下创新绩效动态发展研究

龚茜莹， 梁 鑫

(上海工程技术大学 管理学院， 上海 201620)

0 引 言

随着后金融时代国民经济的缓慢复苏，技术创新已然成为发展中国经济的核心因素。而作为可以进行自主创新也可以进行创新成果转化的主体，企业凭借其独特的可以实现产业化的天然优势，成为研究创新绩效的主要对象。而大中型工业企业又是中国国民经济支持的重要支柱，从一定程度上来说，其大量的科技创新活动的创新效益水平走势能够反映全国工业企业创新活动效益水平的发展趋势[1]。因此，如何看待中国大中型工业企业创新要素资源联动效率的现状，如何充分发挥各要素的协调机制，如何使中国传统制造型工业企业实现核心技术的价值挖掘，已经成为目前重要的研究课题。

通过对现有的国内外相关文献进行研究，可以发现以前有关创新效率评价方面的研究主要还是以非参数法和参数法为主。 其中,参数法的典型代表是由国外学者Meeusen等人[2]所提出的随机前沿分析技术；非参数方法由美国著名经济学家Charnes和Cooper[3]提出的数据包络分析(DEA)表示。相比较国外对创新绩效的评价方法研究，国内学者引用了国外的评价方法，并采用了新的评价方法。雷善玉等人[4]通过DEA-Tobit两阶段模型对中国各省大中型企业的技术创新效率进行了研究。结果表明，企业技术消化吸收能力对其能力产生负向作用；赵继宗[5]从区域角度出发，采用DEA-BCC 模型方法评价甘肃省的大中型工业企业的创新效率，发现其综合创新效率水平处于上升状态；王利[6]通过建立四方程递归模型证明了各创新行为之间存在着互相影响的作用关系；孙丝雨等人[7]采用两阶段网络 SBM模型衡量了黑龙江省科技研发与成果转化过程中技术创新效率的差异，结果表明，该省的技术创新处于波动低效率状态。

在投入产出方面，国外学者认为在影响企业R&D投入与产出转化效率的主要因素包括组织结构、技术水平和组织环境等方面，后继学者也对此进行了广泛的研究。目前，从国内学者的研究现状来看，影响企业R&D活动效率的因素主要分为企业因素和环境因素[8]。陈伟等人[9]利用 DEA- Malmquist法测量了大中型工业企业的创新水平并提出了相关绩效影响指标，结果显示R&D经费投入、R&D人员数和技术要素都会影响企业的创新效率。罗家松等人[10]通过分析各省创新政策对企业的创新绩效的作用水平来分析是否需要调整创新政策，结果表明应当加大对创新绩效产生正向影响的政策，调整和优化对创新绩效产生负向作用的政策。

综上所述，企业创新绩效的研究一直是企业绩效研究中一个非常重要的领域，所涉及的研究范围也非常地广泛。而已有研究更多是基于静态的要素视角，将各个指标单一地作为研究对象来研究，忽略了各个指标之间的相互影响作用。因此，本文首先考虑通过建立由中国大中型工业企业各个相关投入要素指标按熵值法确定权重的子系统所构成的复合系统模型，来分析各要素投入的系统发展关系。然后根据脉冲响应和方差分解来分析各投入要素与创新绩效的动态发展与变化关系，旨在建立一套较为合理的、可以量化分析的企业创新绩效评价体系，以促进各要素作用的价值挖掘。

1 研究理论

(1)系统性原则。在20世纪40年代，国外生物学家Bertalanfi[11]在哲学研讨会上首次提出了一般系统理论的概念，并首次将系统定义为：系统可以说是若干要素在一起相互作用形成的复合体，也可以说是处于一定环境中相互联系中的各组成成分的总体。20世纪70年代，中国系统工程学家钱学森[12]对系统的研究也做出了巨大的贡献，并在《组织管理的技术系统工程》中提出，鉴于运筹学和管理科学在各自领域的发展情况，如果能用系统理论将二者联系起来，那么这不仅是促进运筹学和管理科学结合的一个重要手段，也将为中国在应用系统工程工作上开创一个新的局面。对于一个复杂的系统，既不能用单一的数学形式进行定量研究，而是要求将观察对象看作是若干个小系统处于一定环境中相互作用的结果；又不能片面地、孤立地研究系统内某个小指标或者子系统，而应该从优化系统角度，观察各个变量的特性，通过调整各个子系统的参数来实现系统整体最优。因此，对于企业创新绩效的研究，要具体分析整个活动中所参与的各项要素，不仅要包括自变量的要素，也要包括因变量的要素，以至于各个要素结合起来形成一个有机整体。

(2)创新资源子系统。创新资源要素是企业R&D活动的内生源泉，具体可以分为劳动要素和资本要素。对此可做阐释分述如下。

① 劳动要素。对于劳动要素，经济学家将生产要素中的劳动要素定义为非熟练劳动与熟练劳动的劳动者，即一般的劳动者和具有增值性和稀缺性的高级人才，故本文将劳动要素指标定义为R&D人员全时当量X1和硕博比例X2[13]。

② 资本要素。对于资本要素，除了经营过程中所需要的现金流量外，设备等实物或非实物财务资源也可列入资本的范畴之内。因此，本文选择包含现金流量和设备等财务资源的R&D经费投入X3作为资本要素指标之一。同时，为了反映企业科技活动的创新投入水平，本文选取新产品投入经费X4作为资本要素的另一个指标。

(3)创新技术子系统。创新技术要素是企业R&D活动的内在动力。一般而言，人力和财力往往是企业市场竞争的主导因素，而技术是竞争的决定因素。如果凝结在产品中的技术不能达到市场需求，企业往往处于弱势水平。而为了满足市场需求并获得竞争优势，企业会加大对获得技术知识方面的投入，以及由知识转变为技术的能力上的投入。其中向发达国家引进先进技术，再对其进行消化吸收，在消化的基础上进行改造，是发展中国家进行创新的必要途径[14]。因此，本文选择引进技术经费支出Y1、消化吸收经费支出Y2、购买国内技术经费支出Y3和技术改造经费支出Y4作为技术要素输入指标。

(4)创新环境子系统。创新环境要素是企业R&D活动的外部催化剂，具体可以分为政策环境、企业外部市场环境和制度环境[15]。作为科技创新活动主体之一的企业，一方面其内部R&D活动的不可预测性使本身带有不确定性的市场风险，从而导致企业的实际创新成本高于预期成本，另一方面其创新活动水平可以直接影响到企业市场的外部竞争。因而本文将调节市场经济不平衡、鼓励企业进行创新活动和促进技术经济的增长的国家财政拨款设为Z1，将大中型企业有R&D活动的企业个数设为Z2。同时考虑到公共技术服务平台会为企业创新活动提供技术支撑，将国家技术服务支出设为Z3。

(5)创新绩效子系统。有关企业创新绩效的衡量指标方面，中国有关学者主要提出的设定指标为专利申请数量和新产品销售收入[16]。因此，为了衡量企业创新活动绩效及其有效性，本文将专利申请量指标设为P1，将新产品销售收入指标设为P2。另外，随着社会的进步与需求的变化，开发新产品成为了企业在市场竞争中的核心竞争力，企业将有限的资源利用到优化企业绩效的项目上，成为获得竞争优势的重要手段，因此本文将新产品开发项目数指标设为P3。各指标构成见表1。

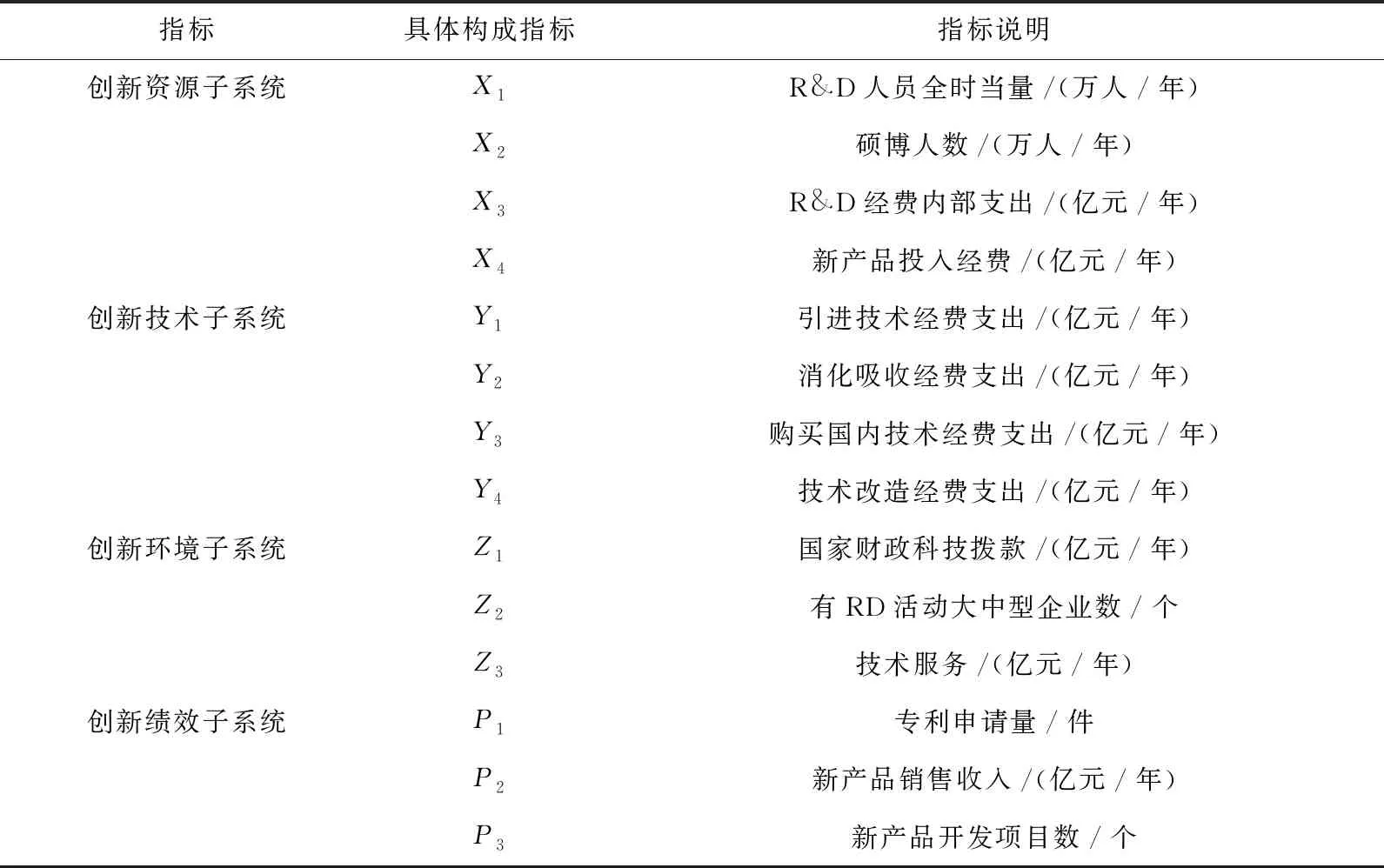
表1 指标体系构建表

2 实证分析

2.1 数据来源

本文以《中国科技统计年鉴》与《中国统计年鉴》发布的数据为基础，选取1999～2017年中国大中型工业企业的指标数据，采用SPSS、Eviews等软件进行实证分析，通过对原始数据进行整理，得到创新资源子系统、创新技术子系统、创新环境子系统的序参量指标数据和创新绩效指标数据。其中，由于创新资源子系统下的硕博比例指标数据在1999～2008年和2009～2017年两个时间段出现口径不一致的情况，本文用换算过的1999～2008年《中国科技统计年鉴》中相关指标数据(研究与试验发展人员全时当量*2009～2017年硕博占比R&D人员全时当量的平均数)代替该时间段的硕博比例指标数据，另外对于个别缺失数值采用均值插补法进行补充。

2.2 复合系统协同度模型构建

2.2.1 复合系统协同度模型理论

借鉴孟庆松等人[17]对复合系统模型的研究，结合中国大中型工业企业的发展实际，首先通过构建复合系统协同度模型测量分析各创新要素投入的协同发展关系。

设创新要素投入复合系统S为包含创新资源子系统sx、创新技术子系统sy和创新环境子系统sz, 即S=f(sx,sy,sz)，子系统j的序参量i为eji，(βji≤eji≤αji,αji、βji分别为最大值*(1+a)和最小值*(1-a)的上下限，a取10%), 则子系统序参量有序度的计算公式为：

dj(eji)=(eji-βji)/(αji-βji),

(1)

由式(1)可知，dj(eji)∈[0,1],dj(eji)的值越大，则表明eji对其子系统的贡献程度越大。从总体上看，各序参量分量eji可通过集成来测量子系统的有序度，本文将运用几何法进行测度，具体计算公式如下：

(2)

(3)

(4)

其中，D(S)∈[0,1] ，D(S)会根据各子系统有序度变化而变化。如一个有序度处于上升趋势的子系统会对复合系统协同水平产生促进作用，而一个有序度处于下降状态的子系统会负向影响整个复合系统协同演化水平。

2.2.2 复合系统协同度模型实证分析

2.2.2.1 熵值法确定权重

为了定量分析中国大中型工业企业的各创新投入要素之间的系统发展关系，先采用熵值法对各子系统序参量进行客观赋权，得出eji在子系统j下的权重。

(1) 计算eji在子系统j下第k年的权重γki，需用到如下数学公式：

(5)

其中，xki为各子系统子指标标准化后的数值。

(2) 计算子系统j下第i项指标的信息熵值φji，需用到如下数学公式:

(6)

φji=1-φji,

(7)

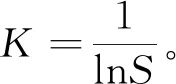
(3) 计算子系统j下第i项指标权重λji，需用到如下数学公式:

(8)

将原始指标数据标准化后带入以上公式(5)～(8)，得到各子系统序参量权重，结果见表2、表3。

表2 子系统序参量权重表1

表3 子系统序参量权重表2

Tab. 3 Subsystem order parameter weight table 2

年份Y1Y2Y3Y4P1P2P31999207.518.113.8845.67 88452 2925 550.02000245.418.226.41 132.611 81955 9537 641.42001285.919.636.31 264.815 33857 4128 793.52002372.525.742.91 492.121 29759 78810 837.82003405.427.154.31 896.431 38268 63314 097.72004367.954.069.92 590.642 31874 57620 421.22005296.869.483.42 792.955 27181 03324 097.12006320.481.987.43 019.669 009100 76031 232.82007452.5106.6129.63 650.095 905112 36940 976.22008440.4106.4166.24 167.2122 076121 35851 291.62009394.6163.8174.73 671.4166 762152 77057 978.12010386.1165.2221.43 638.5198 890159 63772 863.92011421.0178.3203.03 677.8265 612176 04488 650.22012378.0145.7178.13 669.0327 116210 73098 192.22013373.6138.1189.53 495.0359 791222 508112 561.92014365.1131.5190.23 287.2393 480225 206123 600.82015390.6101.6207.22 703.0394 956176 447129 076.62016456.4104.8187.62 622.0438 422195 747147 336.42017370.2114.8182.12 705.1496 260222 448159 956.9权重λji0.1100.3950.2960.1990.3940.2580.348

2.2.2.2 系统有序度实证分析

首先将各创新投入投入子系统的序变量数据xki带入公式(1)进行标准化处理，得出各子系统序变量的有序度dj(eji)；然后将各子系统序变量的有序度dj(eji)的数据带入公式(2)，计算各子系统的有序度dj(sj)，结果数值见表4的2～4列，其变动趋势如图1所示；最后再将表4的2～4列数据带入公式(3)，计算复合系统的有序度D(S)，结果数值见表4的5～8列，其变动趋势如图2所示。

表4 1999～2017年子系统有序度及复合系统有序度

Tab. 4 System order degree and composite system order degree from 1999 to 2017

年份dx(sx)dy(sy)dz(sz)c(sx,sy)c(sx,sz)c(sy,sz)D(S)19990.001 60.003 90.003 1----20000.004 90.013 10.004 40.005 60.002 10.003 50.003 420010.007 90.021 20.005 70.010 50.004 10.006 80.006 620020.011 60.037 60.009 10.018 40.007 80.014 20.012 720030.016 60.049 00.010 50.026 00.010 60.018 30.017 120040.018 30.077 80.013 00.035 20.012 90.027 20.023 120050.033 60.081 00.018 30.049 70.022 10.034 30.033 520060.043 90.093 30.030 00.061 50.033 80.049 10.046 720070.059 90.142 70.042 30.090 00.047 90.073 90.068 320080.076 70.157 30.053 90.107 40.061 80.088 30.083 720090.092 90.164 90.074 10.121 30.080 50.106 90.101 520100.113 10.173 80.093 60.137 70.100 50.124 00.119 720110.138 30.181 20.119 20.155 70.126 00.143 50.141 220120.163 00.157 10.155 70.157 30.157 00.152 90.155 720130.179 10.154 00.184 00.163 30.179 20.164 90.169 020140.190 80.147 40.208 20.164 80.197 00.171 60.177 320150.196 50.135 40.237 00.160 10.213 60.175 40.181 720160.209 10.141 20.270 50.168 80.235 60.191 60.196 820170.219 70.132 10.302 50.167 20.255 60.196 00.203 1

注：表中c(s1,s2)指的是二维度的复合系统，D(S) 是三维度的复合系统

图1 子系统协同度变化趋势图

图2 复合系统协同度变化趋势图

2.2.3 系统有序度结果分析

由图1可知，创新资源子系统和创新环境子系统协同度整体呈上升趋势，这与企业逐步加大对创新资源的投入力度和中国积极推动科技进步、大力发展科技创新的战略有关；创新技术子系统协同度在1999～2001年呈波动上升趋势， 并于2011年达到峰值，随后一直呈现波动下降趋势，这与中国产业技术水平放慢对世界技术前沿追赶速度等因素有关。

由图2 可知，创新资源-创新技术复合系统在1999～2011年的协同演化水平一直处于上升状态，而在2012～2017年处于平缓上升状态，这表明了在2012～2017年技术要素子系统技术自身波动趋势变化对创新资源子系统变化趋势造成了负向冲击影响，使其复合系统的协同发展水平发生回流现象；创新资源-创新环境复合系统协同演化水平在1999～2017年一直处在高速发展状态，这说明了创新资源子系统和创新环境子系统之间的价值融合与交互作用处在一个良好状态；创新技术-创新环境复合系统协同演化水平处于低速发展状态，这表明双方子系统发展的叠加效应影响了二者协同发展趋势，技术子系统的发展变化反向诱导了二者之间的协同发展关系；创新资源、创新技术和创新环境复合系统的协同演化水平在1999～2011年一直处于良好发展状态，而在2012～2017年处于趋势缓慢发展状态，表明了各创新投入要素子系统在2011年之前一直存在着正向的交互作用，而在2011年以后，因为技术要素的波动对整个复合系统产生了抑制作用。

2.3 各要素动态关系分析

运用复合系统协同度模型测量分析了各创新投入要素的协同演化水平之后，需要进一步通过使用 Eviews软件计量分析创新投入要素子系统与创新绩效子系统的动态发展关系以及各个子系统之间的相互影响作用。

2.3.1 单位根检验

为了分析各创新投入要素与创新绩效子系统之间的动态关系，本文采用VAR实证方法，建立VAR模型。为了防止伪回归现象的发生，利用ADF法对Ln(IR)、Ln(IT)、Ln(IE)和Ln(IP)序列进行平稳性检验,检验结果见表5。其中，研究中还将用到如下数学公式:

(9)

(10)

(11)

(12)

检验结果显示，各子系统综合指标Ln(IR)、Ln(IT)、Ln(IE)和Ln(IP)的检验P值均低于显著性水平5%，这即表明Ln(IR)、Ln(IT)、Ln(IE)和Ln(IP)均服从平稳条件。

表5 ADF统计量测算结果

注：检验类型(c,t,k)中的c、t、k分别表示单位根检验方程是否有常数项、时间趋势和滞后阶数

2.3.2 滞后阶数确定与AR根图

根据LR、FPE、AIC、SC和HQ值的5类原则，选取带*的统计量个数最多的滞后阶数，表6显示了滞后阶数为2时对应的检测值带*数量最多，故确定最优滞后阶数L=2，评价结果是建立VAR(2)。当滞后阶数取2时，从AR根图可以看出(见图3)，模型多项式的所有特征根都落在单位圆内，如此则进一步验证了由Ln(IR)、Ln(IT)、Ln(IE)和Ln(IP)序列所建立的VAR(2)模型满足稳定性条件。

表6 VAR模型最优滞后阶数检验结果

图3 AR根检验结果

2.3.3 脉冲响应与方差分解

研究指出，一方面格兰杰因果检验由纽约大学经济计量与统计学的讲席教授Tsay提出。总地来说，格兰杰因果检验只是表达某事件A与另一事件B在时间上的先后顺序，检验A(B)是否对B(A)具有预测能力,而脉冲响应是对事件信息的表达，二者应该不相关[18]。另一方面,考虑到格兰杰因果检验是在基于完整的信息集上做出的统计意义上的判断，而非现实阶段性的经济意义上的因果检验。因此，本文通过事先确定变量经济意义上的相关性，直接通过脉冲响应和方差分解来深入地研究各子系统之间的动态影响关系。对此拟展开研究论述如下。

2.3.3.1 脉冲响应分析

为了进一步考察各创新投入要素子系统与创新绩效子系统相互冲击的影响作用，本文通过稳定的VAR(2)模型，设定冲击响应期为20，对4个变量进行脉冲响应仿真，通过对Ln(IR)、Ln(IT)、Ln(IE)和Ln(IP)分别施加一个单位的冲击之后，各自对Ln(IR)、Ln(IT)、Ln(IE)和Ln(IP)产生的动态影响路径响应图详见图4。

从下方最后一行的冲击响应图可以看出：

(1)如果给创新资源子系统一个单位的正向冲击之后，将会在第一期对创新绩效产生波动性的正向影响，并在第六期达到最大值，此后的影响将会慢慢减弱。原因在于创新资源作为创新绩效的最基本的内生源泉，对其增大投入力度，可以直接对创新绩效产生促进作用。但可能由于资源溢出的影响，在响应前期会出现阶段性正负影响交替情况。

(2)如果给创新技术子系统一个单位的正向冲击，将会在第二期之前产生微弱负向影响，并在第二期开始对创新绩效产生正向影响，而且大约在第四期达到最大值，随后影响将会慢慢减弱。原因在于企业对创新技术要素的投入过程存在滞后现象，当期技术要素的投入需要一个吸收转化过程才能对企业的创新绩效起到促进作用。

(3)如果给创新环境子系统一个单位的冲击，将会对创新绩效产生正向影响，并大约在第二期达到最大值，随后影响将会慢慢减弱。原因在于创新环境作为企业的外部条件，提高对其的投入力度，可以直接正向作用于企业的创新绩效。但由于作为R&D活动的重要主体的企业本身所具有的自主特性，决定了外部条件的影响作用只是起到一个短暂的促进作用。

(4)创新环境对创新绩效的正向冲击影响程度明显低于创新资源和创新技术对创新绩效的正向影响程度，可能是因为企业没有合理安排财政科技资金，以至于在整个R&D活动中由于个别环节不恰当的投入而发生了资金挤出效应。

从其余的图中可以得知：

(1)创新资源与创新技术存在互为反哺的现象，一方面创新资源的投入力度增大后可以增加对创新技术的投入，另一方面在创新技术有了基础研究的支撑后会促进创新资源的投入。

(2)创新环境对创新资源有正向波动促进作用，创新资源对创新环境有滞后影响作用，这可能跟外部条件运作机制有关。

(3)创新环境对创新技术有着微弱影响，创新技术的沉淀与发展可以促进外部条件的提升。

图4 脉冲响应图

2.3.3.2 方差分解

为了进一步了解变量变动的相对重要性，本文通过方差分解来分析扰动项对变量变动的贡献度，计算每个变量对总贡献的占比例，设定响应期为20，对创新绩效子系统的方差进行分解的方差结果如图5所示。由图5中最后一张图可知：大约从第14期开始，取对数后的创新绩效子系统Ln(IP)的预期波动中约有33% 由取对数后的创新资源子系统Ln(IR)的波动解释，有38% 由取对数后的创新技术子系统Ln(IT)的波动解释,剩下3%的信息由取对数后的创新环境Ln(IE)波动解释。由剩下的图可以得知：Ln(IR)的波动主要由Ln(IT)和Ln(IP)波动解释，Ln(IT)主要由Ln(IR)波动解释，Ln(IE)主要由Ln(IR)、Ln(IT)和Ln(IP)共同解释。

图5 方差分解

3 结束语

由复合系统模型实证结果可知，中国大中型工业企业各创新投入要素在1999～2017年之间处于波动协同演化状态，创新资源子系统和创新环境有序度的上升趋势和创新技术子系统有序度的阶段性的下降变化分别对各创新投入要素子系统和复合系统有序度的变化趋势造成交互影响。由脉冲响应和方差分解可知，创新绩效的波动变化主要由创新资源和创新技术波动解释，少数由创新环境波动解释。因此，可以考虑通过调节创新资源与创新技术的投入，注重外部环境的创新能力，来提高企业的创新绩效。研究给出应对策略和建议如下。

(1)调节创新资源要素的投入。企业的科技创新不仅需要充足的资金来维持基本的R&D活动，也需要高素质水平的人才与团队来提高R&D活动的质量。资金与人才是企业进行科技创新的内生源泉，而中国大中型工业企业的科技创新水平目前还处于发展初期的较低水平，正需要这些必要的条件来支撑。因此，企业一方面可以通过适当地加大科研经费的投入和鼓励企业技术研发中心实行独立财务核算来提高创新效率，节约创新成本；另一方面可以通过构建高素质科技人才交流平台和实施高素质人才激励政策来引进和保留技术人才队伍。

(2)调节创新技术要素的投入。由复合系统协同度模型的实证结果可以得出，中国大中型工业企业存在累计经验不足、技术创新知识缺乏和创新能力基础较为薄弱的缺点；由脉冲响应和方差分解可以得出，中国大中型企业目前对企业的技术创新的投入力度还保持着较低水平，这严重阻碍了企业创新发展的效率。而从企业本身来说，企业可以通过一系列对先进技术进行引进、吸收与转化的活动将被动创新转化成主动创新。也就是说，在企业希望产品的核心技术可以取得突破性发展，但自身又无法进行完全自主研发的情况下，企业可以先利用外部渠道获得一定的技术基础，然后通过消化吸收累积一定的技术经验，最后以较低的经济成本实现被动性创新向主动性创新的转化。

(3)加强对外部创新环境的重视。从政府角度来说，政府应当构建良好的贸易环境与沟通渠道，加快落实创新政策的步伐，在以企业研发为主要手段，政府引导为途径的情况下，合理调整财政科技投入与技术服务的成本，实现创新资源的合理配置。从企业角度来说，一方面企业应结合自身技术的创新特点，加强对外部资源的合理利用，合理分配创新活动中的各个环节支出，实现内部资源的优化配置。

另一方面企业应加强与外界的技术研发合作，提升自主创新意识，在不断吸收改造技术的过程中提升企业自主创新能力。