关系数据模型中函数查询的结构特征

吴文莉， 刘国华,

(1 东华大学 计算机科学与技术学院, 上海 201620; 2 上海市数据科学重点实验室(复旦大学)， 上海 201203)

0 引 言

查询(即，由数据库到关系的函数)和查询语言(即，用于表示这一函数的语言)[1]一直以来都备受人们关注。Codd于1970年提出关系数据模型后，关系模型的查询及查询语言成为研究热点，出现了一批具有影响力的研究成果，如一阶关系演算以及关系代数[2-3]、合取查询[4]、表查询[5]、函数查询语言[6]等。

近年来，随着大数据地位的提升，如何在大数据环境下准确、高效地得到查询结果是函数查询亟待解决的问题，其中如何解决查询解答问题一直是人们关注的重点问题。大数据为查询解答带来了挑战，大数据查询的计算复杂性不再类似传统查询[7]。文献[7]对查询解答问题难易程度的判定提出了形式化的方法，并对预处理问题进行了研究，提出了数据驱动的预处理和查询驱动的预处理两种方法。文献[8]明确了大数据环境下查询解答问题难易程度的划分标准，对什么查询在大数据上是易处理的、如何求解大数据查询的复杂性等问题给出了一系列预处理方案，对查询解答问题的近似求解算法进行了探讨。

在大数据应用环境下，函数查询成为主要操作，如函数查询语言可以用于定义大数据上的分析查询，用其结果定义各种执行任务[9]。为了便于表示大数据上的函数查询，Nicholas等人[9]提出一种高级函数查询语言(HIFUN)，但没有给出函数查询的形式化定义，也没有对函数查询的结构特征及复杂性问题进行研究。函数查询的结构特征是分析查询解答复杂性的基础，本文以关系数据模型为对象，对经典的关系数据库进行了扩充定义。在此基础上，给出函数查询的形式化定义，分析函数查询的可计算性，用一阶语言描述函数查询，并证明函数查询的结构是一阶查询层次结构。

1 扩充数据库及函数查询

文献[10]对数据库的结构特征进行了详细分析并且给出了经典结论，但在其数据库的定义中忽略了属性的描述，因此该定义不适用于函数查询的结构特征研究。本文针对文献[8]中数据库的定义进行扩充，文献[10]关于数据库的定义如下。

例1举出一个数据库B的实例。论域U= {2,3,4,5}，数据库B= (D,R1,R2)，D= {2, 3, 4, 5}，R1= {(2, 5), (4, 2), (4, 3), (5, 2)} ⊂DD，R2= {4, 2} ⊂D，见表1、表2。k= 2，a1= 2，a2= 1。

表1 例1中的关系R1

表2 例1中的关系R2

以上定义的不足之处是没有给出属性的描述，为了扩充数据库的定义，把属性看作函数。给出属性的形式化定义如下。

(1)

其中，l表示行号，i表示列号，ti是一个如下形式的函数：

ti:ROCO→D，

其中，RO表示行号的集合，CO表示列号的集合。由函数ti确定Attj中每个属性Ai的属性值。

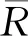
(2)

其中，l表示行号，i表示列号，eti是一个如下形式的函数：

eti:Dc→U，

其中，Dc表示Attj中某些属性的属性值的笛卡尔积。由函数eti确定属性EAi的属性值。

扩充数据库的定义如下。

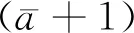
例2举一个扩充数据库Bf的实例。论域U= {2, 3, 4, 5, 6, 7}，扩充数据库Bf= (D,R1,R2,S1,S2)，其中D= {2, 3, 4, 5}，R1= {(2, 5, 7), (4, 2, 6), (4, 3, 7), (5, 2, 7)} ⊂UUU，R2= {(4, 6), (2, 3)} ⊂UU，关系R1、R2分别见表3、表4。S1= {A1,A2,EA1}，S2= {A3,EA2}。k= 2，(a1+1) = (2+1)， (a2+1) = (1+1)。其中扩充属性集EAtt= {EA1,EA2}。

表3 例2中的关系R1

表4 例2中的关系R2

下面给出函数查询的形式化定义。

满足以下条件：

(1)Qf满足部分递归。

(2) 如果Qf(Bf)有定义，Qf(Bf)⊂Ub且Qf(Bf)是有限的。

(3) 如果函数查询满足：函数查询是部分递归并且满足一致性条件：如果BfhBf，那么Qf(Bf) =h(Qf(Bf))，那么函数查询是可计算的。

补操作与组合操作是查询中的2个基本操作，现给出函数查询中补操作和组合操作的定义。

(3)

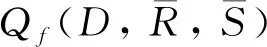
C= {Qf|QfC}，

(4)

例3已知有例2所示的扩充数据库Bf= (D,R1,R2,S1,S2)，以及扩充数据库Bf上的函数查询Qf，如果查询结果的秩b= 2，那么函数查询Qf可以表示为：

Qf:{Bf= (D,R1,R2,S1,S2)}2(UU)

函数查询Qf的查询结果见表5。

表5 Qf的查询结果

Qf(Bf) = {(7, 4), (6, 2), (7, 2)}

(5)

例4举出一个扩充数据库Bf的实例。论域U= {2, 3, 4, 5, 6, 7, 12, 15}，扩充数据库Bf= (D,R1,R2,R3,S1,S2,S3)，其中D= {2, 3, 4, 5, 6}，R1= {(2, 5, 7), (4, 2, 6), (4, 3, 7), (5, 2, 7)} ⊂UUU，R2= {(2, 4, 6), (4, 2, 3)} ⊂UUU，R3= {(3, 5, 15), (2, 6,12)} ⊂UUU，关系R1、R2、R3分别见表6～表8。S1= {A1,A2,EA1}，S2= {A1,A3,EA2}，S3= {A2,A4,EA3}。即k= 3，(a1+1) = (a2+1) = (a3+1) = (2+1)。

表6 例4中的关系R1

表7 例4中的关系R2

表8 例4中的关系R3

已知有如上扩充数据库Bf,Bf上的函数查询Qf，Qf1，Qf 2，其类型分别为(1，1)2，(2+1)1，(2+1)则的查询结果见表9。

表的查询结果

2 函数查询层次结构

查询语言是用来描述查询的工具[11]，为了从理论上研究查询问题，人们通常使用一阶语言描述查询[10]。本文的研究也是基于一阶语言，下面给出描述函数查询的一阶查询语言的定义。

定义7 一阶语言L是没有函数符号，具有等式的一阶语言，R1，R2，…作为关系符号，其中Ri是具有扩充属性的关系，使用符号Ri表示关系及作为关系本身，关系Ri的元数隐含在上下文中。FO表示由以下表达式组成的语言:

(6)

例5如下表达式:

(x,s2)(R1,R2)(y)(R1(x,y,s1) ∧R2(y,s2))

定义8 一阶查询QfM记为由M表示的函数查询，MFO，QfW= {QfM|MW}，W⊂FO。集合QFO是一阶查询的集合，并用F表示。

例6令M为(x,s2)(R1,R2)(y)(R1(x,y,s1) ∧R2(y,s2))，则M为(x,s2)(R1,R2)(y)(R1(x,y,s1) ∨R2(y,s2))。

引理1对于任意MFO，有Qf(M)=QfM，对于任意W⊂FO，有Qf(W)=QfW。

同样地，定义替换操作类比函数查询中的组合操作。

例7令M=s1.(T1,T2).(y)(T1(x,y,s1) ∧T2(y,s2))，N1= (y,s4,z).(R1,R2).(w)(R1(y,z,s3) ∨R2(w,z,s4))，N2= (u,s6).(R1,R2).(y)(R1(u,u,s5) ∧R2(u,y,s6))，那么M∘=s1.(R1,R2).(y)((w)(R1(s1,s1,s3) ∨R2(w,s1,y)) ∧ (z)(R1(s1,s1,s5) ∧R2(s1,z,y)))。

定义11对于集合W，V⊂FO，其组合操作记为W∘V= {M∘ (N1,N2, ... ,Nn) |MW，NiV，1≤i≤k}。

易证得出研究引理，详见如下。

引理2对于任意M，(N1,N2, ... ,Nn)FO，有Qf(M° (N1,...,Nn))=QfM∘Qf(N1,...,Nn)。对于任意集合W，V⊂FO，有Qf(W ∘ V)=QfW∘QfV。

定义12 存在查询EX表示如下形式的表达式集合：

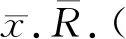
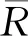
引理3对于任意函数查询集合C，有：

C∪C⊂E∘C=E∘C=E∘ (C∪C)

证明函数查询是函数。令C1为集合C中的任一函数查询，其定义域为D1，值域为Rn1，则C1的定义域为D1，值域为Rn1，令E1为集合E中的任一存在性函数查询，其定义域为D2，值域为Rn2。那么有：

(E1∘C1):D1Rn2，

(E1∘C1):D1Rn2，

(E1∘ (C1∪C1)):D1Rn2，

综上所述，引理3成立。

本文将属性视为函数，对数据库重新定义，经过研究发现，函数查询的层次结构与多项式时间层次结构[12]、一阶查询层次结构[10]等已知层次结构相似。

下面给出表达式集合的层次结构的定义，由此引出函数查询集合的层次结构。

定义13 表达式层次结构表达式集合FO的集合{∑i，Γi}i<ω定义如下：

(2)∑i+1=EX∘Γi，

(3)Γi=∑i，

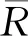
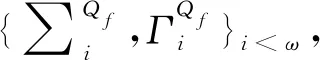
由引理1～3可以得出：

引理4令0(与0相等)记为一阶语言L中无量词的表达式集合，i+1(分别为i+1)记为(则对应于(形式的表达式集合，其中Ψ在i(对应于i)中且在Ψ中是自由的，那么：

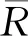
证明(1) 当i= 0时，0为一阶语言L中无量词的表达式集合，∑0为|Ψ无量词}，由定义可知i=0时成立。令Ψ表示((Θ表示或者)，Ψi+1。令N表示i。假设N在Γi中，令M表示则M在EX中，M∘N在中，由定义可知M∘N在∑i+1中。由公式i+1推导出Γi中的表达式的证明类似。

关系查询语言主要有2种类型，一种是逻辑语言，比如关系演算，由公式组成；另一种为代数语言，比如关系代数，由程序组成，其基本操作是代数(如连接和投影)[13]。文献[14]证明了关系演算与关系代数在语言表达能力上的等价性。因此，一阶查询层次结构同样可以对前述定义的集合进行投影来定义。如果用P表示如下形式的表达式的投影查询集合：

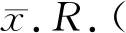
(7)

那么，可以得出：

由引理4还可以得出结论：一阶层次结构可以精确描述一阶查询集合F。

组合可以看作是执行查询、保存查询结果中间值的一种方式，任何可以将查询结果存储在数据库中的查询语言，都可以计算一阶查询[10]。组合是文献[15]中计算所有一阶查询的方式，因此组合具有文献[2]中提到的完备性。

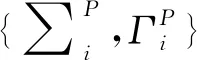
定理3对于任意的i以及扩充数据库Bf= (D,R1,R2, ... ,Rk,S1,S2, ... ,Sk)，其中Bf中的关系Ri{ }并且RiDai+1，集合N|N∑i并且QfN(Bf)}在中是完备的。

(1) 首先证明G如引理4(2)的证明，任意N∑i，N可以转化为等价的表达式其中关系具有扩充的属性的关系，Φ是无量词的，并且转化过程中其符号数量没有增加。那么当且仅当(存在适当的多项式poly)：

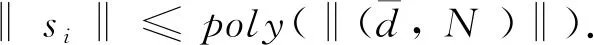
(8)

令T是Bf中的关系，T{ }且TDai+1。给定如下形式的量化布尔公式Ψ:

其中,Pi,ki是命题符号。当且仅当Ψ为真时， ((),N)G成立。其中N为表达式：().∑i。由量化布尔公式的完备性[12]可以得出G在中的完备性[10]。

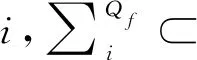
类似证明见文献[10,17]。

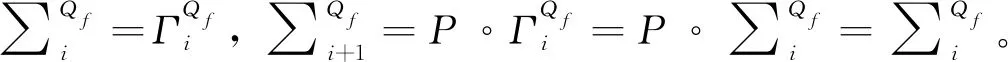
文献[18]从类型角度给出相似证明，其证明2个长度相同的量化前缀在有限数据库上没有相同的表达能力。例如公式逻辑上不等于任何公式，反之亦然。

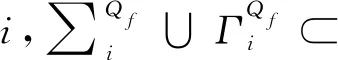
3 结束语

大数据环境下函数查询解答的复杂度问题是制约大数据查询的瓶颈，解决该问题的关键首先是了解函数查询的层次结构特征。本文的研究成果为下一步研究基于函数查询结构特征的查询解答复杂度分析奠定理论基础。