用Hirota双线性方法构造一种(3+1)维高维孤子方程的多孤子解
彭亚丽,套格图桑
(内蒙古师范大学数学科学学院,内蒙古 呼和浩特010022)
1.引言
求解非线性发展方程的精确解,是孤子理论的重要研究内容之一.最近,对于非线性发展方程提出多种求解方法.比如:Hirota双线性方法,是直接引进双线性导数的概念,将非线性发展方程转化成双线性形式的发展方程.在此基础上,利用多种函数变换与计算机代数系统相结合的方法,可获得多种新解.这种方法,在高维非线性发展方程的求解与相关问题的研究中被广泛应用.文[1]利用Hirota双线性方法和试探函数相结合的方法,研究了一个(3+1)维非线性演化方程的求解与约化问题,获得了新结论.文[2-4]利用Hirota双线性方法构造了(3+1)维NLEE方程和(2+1)维Kadomtsev-Petviashvili(KP)方程等非线性发展方程的Lump 解等多种新解.文[5-6]利用Hirota双线性方法,研究了(3+1)维高维孤子方程的求解与解的性质问题.

文[5]利用Hirota双线性方法,研究了高维孤子方程(1.1)的Lump解与线孤子解的相互作用等问题.文[6]利用Bäcklund变换,获得了高维孤子方程(1.1)的双线性形式的Bäcklund变换,由此获得特殊的孤子解.
本文基于文[5-9],首先,通过一种函数变换与对数变换,将(3+1)维高维孤子方程化成双线性方程.然后,用级数扰动法,给出了多孤子解.最后,用有理多项式试探函数法,获得了怪波解,并分析解的性质.
2.(3+1)维高维孤子方程的多孤子解与怪波解
下列求解方程(1.1)的多孤子解:
在方程(1.1)中令

其中ξ=αx+βy+γt,而且α,β,γ是任意非零常数.
将(2.1)式代入方程(1.1)后得到如下方程:
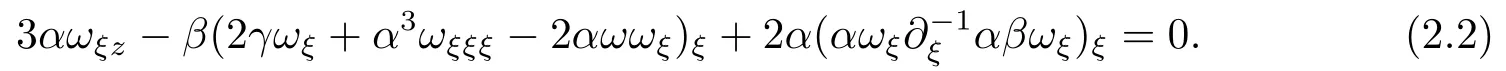
方程(2.2)经对ξ积分可得到:

在方程(2.3)中设

其中ω0是任意非零常数.
将(2.4)式代入方程(2.3)整理得:
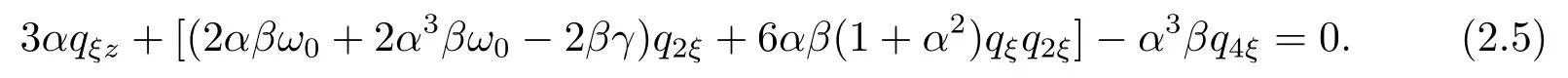
基于文[3-5]中的定义E(q)=3αPξz+(2αβω0+2α3βω0−2βγ)P2ξ−α3βP4ξ=0,再利用文[3-5]获得的结论和定义q=ln(f(ξ,z))⇔ω=ω0+3qξ=ω0+3[ln(f(ξ,z))]ξ,把方程(2.5)写为如下双线性方程:

则有:

将(2.7)式代入方程(2.6)得到:

利用双线性形式及文[10-12]中的小参数扰动法,下面求解方程(1.1)的多孤子解.设

这里f是关于ξ,z的待定函数.
将(2.9)式代入双线性方程(2.6),并比较ε的同次幂系数得到线性微分方程组:

情形1 单孤子解.为了求解单孤子解,设
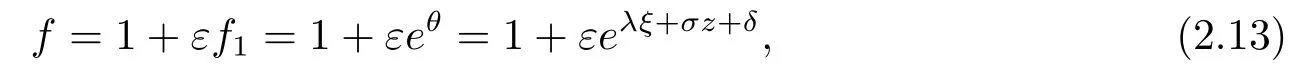
这里λ,σ,δ为常数.
将(2.13)式代入方程(2.10)后得到
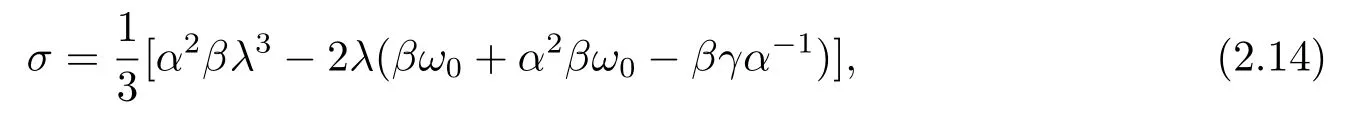
令ϵ=1时,得到单孤子解:

情形2 双孤子解.为了求解双孤子解,设

其中f1=eθ1+eθ2,θi=λiξ+σiz+δi,且λi,σi,δi(i=1,2)都是非零常数.
将(2.16)式代入(2.10)式得到:

将(2.17)式代入(2.11)式求得:

令ε=1时,得到双孤子解:
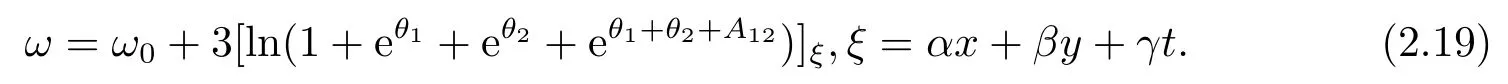
情形3 N-孤子解.根据单孤子解和双孤子解,用数学归纳法推断N-孤子解:

为了求解方程(1.1)的怪波解,设方程(2.8)中的f为

其中ci,j是任意非零常数.
将(2.21)式代入方程(2.8),并ξizj(i,j=0,1,2,3,4)的系数为零后得到一组非线性代数方程组.当

时,借助计算机代数系统Mathematica,求出方程组的如下七组解:
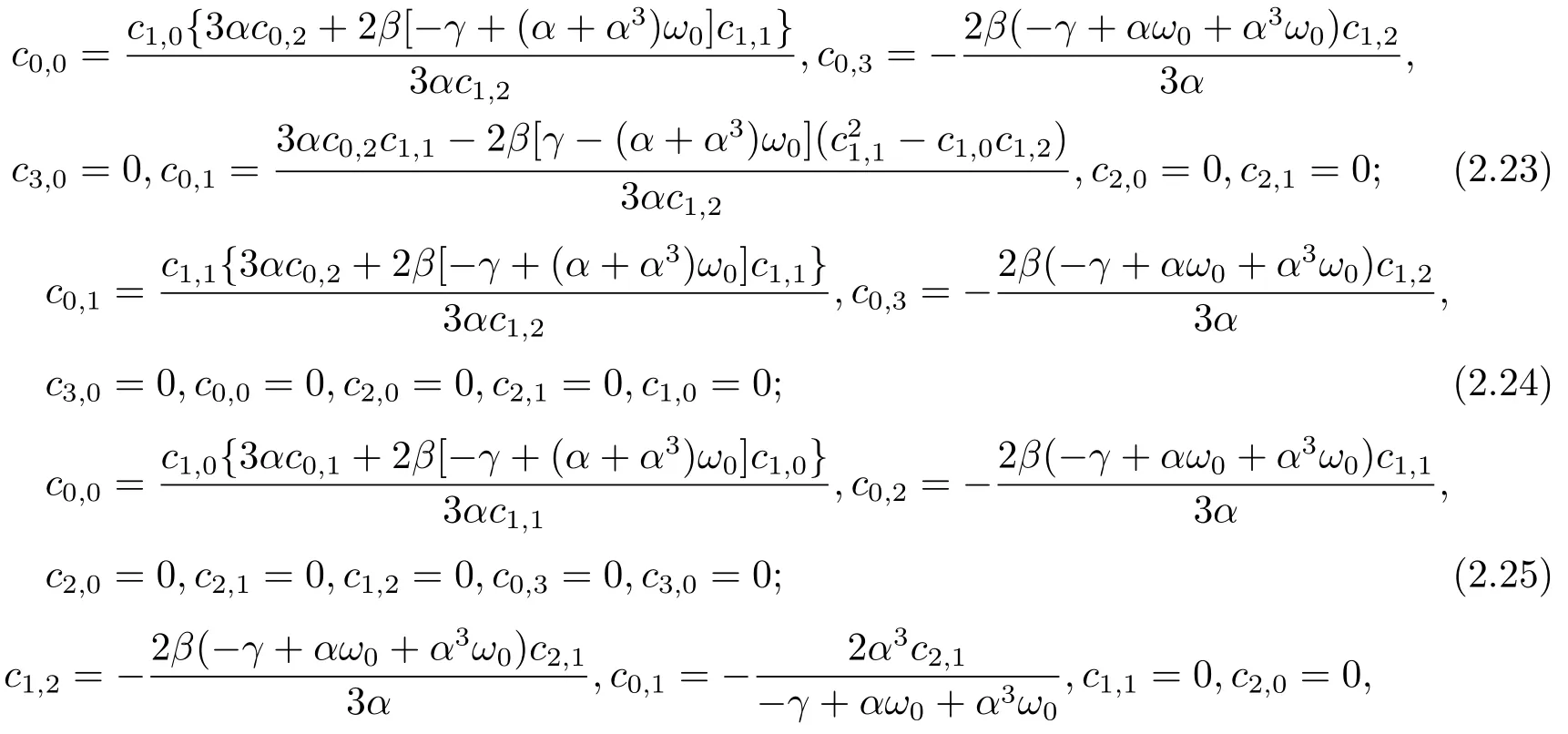

将以上七组解代入(2.21)式中得到f的七组结论:

将以上七种结论分别代入ω=ω0+3 ln(f)ξ,在利用ξ=αx+βy+γt得到方程(1.1)的以下怪波解:

当c0,0=2,c0,1=3,ω0=8,c1,1=4,c0,2=2,c1,2=1,β=2,γ=2,α=2,c2,0=2,c2,1=2,c1,0=3时,怪波解(2.37)的三维图如图1所示,平面图如图2所示.怪波解(2.42)的三维图如图3所示,平面图如图4所示.图1与图3都呈现出上下尖峰波.
3.结语
基于文[1-6]给出一种函数变换与对数变换,将(3+1)维高维孤子方程化为双线性形式.在此基础上,用级数扰动法,给出方程(1.1)的多孤子解.基于文[13-14],用广义有理多项式的试探函数法,获得了方程(1.1)的怪波解.

图1

图2
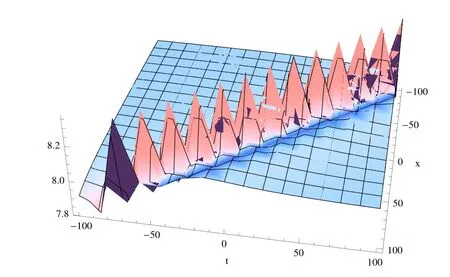
图3

图4
- 应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性

