G-锥度量空间中的不动点定理
黄琪,薛西锋
(西北大学数学学院,陕西 西安710127)
1.引言
文[1]提出了G-锥度量空间的概念,并得出了一些不动点定理.文[2-4]研究了不同压缩条件下的不动点和公共不动点定理.随后,2016年,文[5]在改变文[1]的压缩条件下研究了G-锥度量空间中压缩映射的不动点定理,使得出的定理更具一般性.本文在文[5]的基础上,通过引入新的压缩条件,得出了新的不动点定理,并且得出了在弱相容自映射下的公共不动点定理.
2.预备知识
定义2.1[1]设E是一个实Banach空间,P是E的一个非空闭子集,R是实数集,若满足:
1)P≠ {θ},θ为E的零元;
2)∀a,b ∈R,a,b ≥0和∀x,y ∈R,都有ax+by ∈P;
3)P ∩(−P)=θ,
则称P为E中的一个锥.设x,y ∈E,若x ≤y当且仅当y−x ∈P和x ≪y当且仅当y−x ∈∫P,则称“≤”和“≪”都为E中的偏序,这里∫P表示P的内部.若∫P≠∅,则称P为体锥,如果对∀x,y ∈E,都存在常数M >0,使得当θ ≤x ≤y,都有||x||≤M||y||,则称P为赋范向量空间(E,||·||)中的正规锥,而满足上式的最小的M称为P的正规常数.
定义2.2[1]设X是非空集,假设映射G:X×X ×X→E,满足:
1)∀x,y,z ∈X,G(x,y,z)=0⇔x=y=z;
2)∀x,y ∈X,当x≠y时,G(x,x,y)>0;
3)∀x,y,z ∈X,当y≠z时,G(x,x,y)≤G(x,y,z);
4)∀x,y,z ∈X,G(x,y,z)=G(x,z,y)=G(y,x,z)=···(关于这三个元素满足对称关系);
5)∀x,y,z,a ∈X,G(x,y,z)≤G(x,a,a)+G(a,y,z).
则称G为X上的一个广义锥度量,称(X,G)为G-锥度量空间.
定义2.3[4]设X是一个G-锥度量空间,{xn}⊂X,
1)∀c ∈E且c ≫θ,存在正数N,当∀m,n,l >N时,有G(xm,xn,xl)≪c,则称 {xn}为X中的Cauchy列;
2)∀c ∈E且c ≫θ,存在正数N,当∀m,n >N时,有G(xm,xn,x)≪c,则称 {xn}为X中的收敛列; 其中x为X中的一个固定点,称序列 {xn}⊂X收敛于x.
若X的每个Cauchy列在X中都是收敛的,则称G-锥度量空间完备.
定义2.4[3]设X是一非空集合,映射f,g:X→X,若存在x ∈X,使得ω=fx=gx,则称ω ∈X是f和g的叠合点.
定义2.5[3]设X是一非空集合,映射f,g:X→X,对任意u ∈X,如果fu=gu,都满足fgu=gfu,则称(f,g)弱相容.
命题2.1[2]设(X,d)是锥度量空间,=∅,{xn}是X中的序列,如果 {xn}收敛,则 {xn}的极限唯一.
命题2.2[2]设x ∈E,{xn}是E中的序列,θ ≪c(c ∈E),对θ ≪xn且||xn||→0(n→∞),则存在正整数N,使得当n>N时,有xn ≪c.
命题2.3[2]设x ∈E,∀θ ≪c(c ∈E),有θ ≤x ≪c,则x=θ.
引理2.1[1]设(X,G)为G-锥度量空间,则以下结果等价:
1){xn}收敛于x;
2)G(xn,xn,x)→0(n→∞);
3)G(xn,x,x)→0(n→∞);
4)G(xm,xn,x)→0(n,m→∞).
引理2.2[1]设(X,G)为G-锥度量空间,∀x,y,z,a ∈X,有以下结论成立:
1)G(x,y,z)≤G(x,x,y)+G(x,x,z);
2)G(x,y,y)≤2G(y,x,x);
3)G(x,y,z)≤G(x,a,z)+G(a,y,z);
4)G(x,y,z)≤(G(x,y,a)+G(x,a,z)+G(a,y,z));
5)G(x,y,z)≤G(x,a,a)+G(y,a,a)+G(z,a,a).
引理2.3[3]设X是一非空集合,f,g是X中的自映射,(f,g)弱相容,假设f,g有唯一的叠合点,即ω=fx=gx,则ω是f,g的唯一公共不动点.
3.主要定理及结论
定理3.1设(X,G)是完备的G-锥度量空间,设映射T:X→X,∀x,y,z ∈X满足条件:
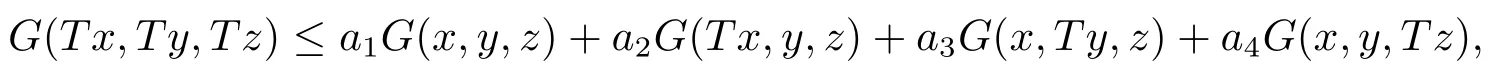
其中a1+2a2+a3+a4<1且a1>2a2,ai >0(i=1,2,3,4),则T在X中存在唯一不动点.
证给定x0∈X,令xn+1=Txn,则

可得

即


易知||δn−1G(x2,x1,x0)||→0,由命题2.2知,G(xn+1,xn,xn−1)≪c,从而 {xn}是X中的Cauchy列.
由X的完备性知,存在x∗∈X,使得xn→x∗(n→∞),从而

其中

整理可得

即

由引理2.1得

因为1−4a2−a3−a4>0,所以G(x∗,x∗,Tx∗)≤0,易知G(x∗,x∗,Tx∗)≥0,故G(x∗,x∗,Tx∗)=0.由定义2.2知x∗=Tx∗,若存在另一个不动点y∗,使得y∗=Ty∗,则
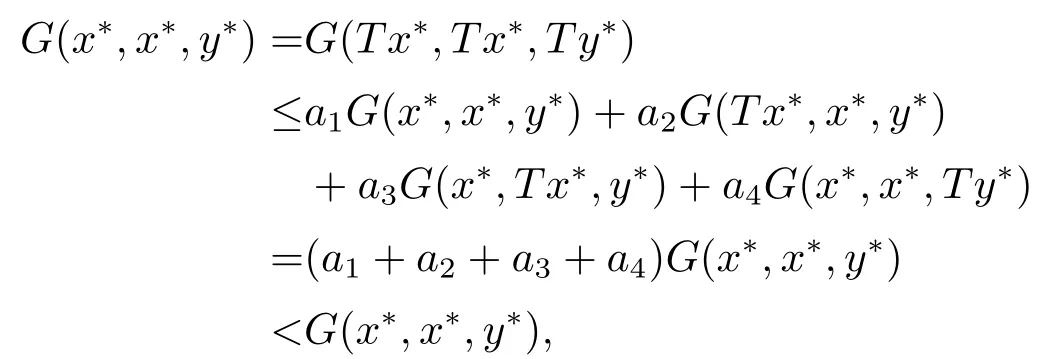
显然不成立,故x∗是T的唯一不动点.
推论3.1设(X,G)是完备的G-锥度量空间,映射T:X→X,对∀x,y,z ∈X满足条件:

则T在X中存在唯一不动点.
证令定理3.1中的结论易证.
定理3.2设(X,G)是完备的G-锥度量空间,S,T是X上的自映射,若对任意x,y,z ∈X,有

成立,其中2b1+b2+b3<1且b1,b2,b3∈(0,1),假设T(X)⊆S(X),S(X)是X的完备子空间,S,T均连续,(S,T)弱相容,则S,T存在唯一的公共不动点.
证给定x0∈X,设Tx0∈T(X),因为T(X)⊆S(X),所以有x1∈X,使得Tx0=Sx1,令ω1=Tx0=Sx1,又Tx1∈T(X)⊆S(X),所以有x2∈X,使得Tx1=Sx2,令ω2=Tx1=Sx2,依次下去,有Txn−1=Sxn,令ωn=Txn−1=Sxn(n=1,2,3,···),下证 {ωn}是X中的Cauchy列.

即


易知||λn−1G(ω2,ω1,ω0)||→0,由命题2.2知,G(ωn+1,ωn,ωn−1)≪c,任取n,m,l,且n 即 由命题2.2知,G(ωn,ωm,ωl)≪c,故 {ωn}是X中的Cauchy列.又因为S(X)是X的完备子空间,所以存在y ∈S(X),使得 因为S,T均连续,所以 下证Sy=Ty. 当n→∞时,得 有 因为1−(b1+b2+b3)>0,因此G(Ty,Sy,Sy)=0,即Sy=Ty,所以y是S,T的叠合点,唯一性易证.又因为S,T是弱相容的,由引理2.3知,y是S,T的唯一公共不动点.





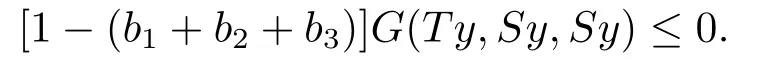
- 应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性

