有限温度下基于NJL模型的GMOR关系研究

蔡文华, 王庆武

(四川大学物理学院, 成都 610065)

1 引 言

众所周知,作为描述夸克—胶子相互作用的有效理论,量子色动力学(QCD)是粒子物理标准模型中相当重要的一部分. QCD理论是研究自然界四大基本相互作用之一—强相互作用的理论. 而动力学手征对称残缺(DCSB)和夸克颜色禁闭是QCD的两个基本特征. 研究QCD相图的学者可能会对有限体积和非零夸克化学势条件下的手征非禁闭相变感兴趣. 因为通过这些研究,我们希望可以得到对自然和早期宇宙更加深刻的见解. 由于QCD复杂的非阿贝尔特征,人们现在很难对DCSB和夸克禁闭有一个全面的理解. 在QCD微扰领域中,即有大量动量传递的过程,由于其有效耦合常数很小,因此可以直接以微扰的方法去研究. 然而,在只有少量动量传递的过程,耦合常数变得很大并且开始波动. 在这些强耦合的非微扰领域,我们倾向于使用非微扰的有效理论来研究相关问题,例如格点QCD模型[1],DSE模型[2]等. 本文使用的NJL模型[3]便是研究非微扰问题比较成功的一个理论.

NIL模型作为一个成功的理论模型,被广泛用于研究在QCD临界点附近的保守电荷涨落. 在NJL模型中,夸克和胶子是基本的自由度,其所有的作用项都被简化为了四体相互作用. 并且,它的拉格朗日方程是建立在自然界中已经被观测到QCD的基本对称现象之上. 尽管在NJL模型中没有夸克禁闭实现的机制,但它现在仍是研究非微扰QCD简单有效的方法.文献[4-7]介绍了NJL模型最新的一些应用.

基于热力学与统计物理的建立和大量实验数据的积累,目前对一些宏观物质的相变研究已经非常熟练[8],但对于核物质的相变来讲还处于摸索前进状态. 这是由于对核物质的认识还有许多不确定的地方,其中就包括核物质的QCD相结构和其高温非零重子化学势下QCD相图上相变点的存在性. 尽管对于一些保守量,例如重子、电荷量和奇异数等的起伏在相对论重子碰撞中能相对比较容易地被检测到,但仍需构建模型来对实验获得的数据进行解释,并进一步检验模型的合理性.

在零温条件下,Gell-Mann-Oakes-Renner(GMOR)关系[9]在低阶近似下严格成立. 由于夸克真空不能被直接观测,它常被用来定义零温下的夸克凝聚值. 但当使用各种模型并将其推广到有限温条件下时,GMOR是否仍然成立并可被利用？如果不成立,又由什么原因引起？这些都是值得研究的问题. 本文内容做如下安排:第二部分根据NJL模型和PTR方案推导出有限温度下夸克有效质量随温度变化的关系[10];第三部分会导出NJL模型下π介子衰变常数和π介子质量随温度的变化, 从而研究GMOR关系在该方案下的成立曲线. 结论在第四部分.

2 NJL模型和PTR方案

由于本文使用NJL模型,故使用以下拉格朗日密度(本文的所有计算都将在欧式空间进行,并且取味Nf=2,取色Nc=3).

LNJL=LO+LI=

(1)

尽管NJL模型的成功表明在某种程度上如此简单的一个模型也能抓住QCD的某些关键要素,但是,由于该模型不涉及重整化,因此需要引入一些表征相互作用截断的动量标度来避免可能的紫外发散以及红外发散. 下面的工作将把正时正规化(proper time regularization)方案的双截断版本(PTR-2)运用于双味NJL模型,并使用传统的方法来修正参数. PTR-2的关键方程为:

(2)

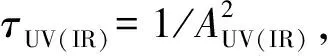
在方程(1)的平均场近似中,有效夸克质量M通常能通过自洽能隙方程决定:

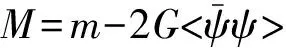
(3)

而该式中双夸克凝聚被定义为:

(4)

其中G(p)为带色夸克的传播介质,它的迹与味、色和狄拉克空间有关.根据洛伦兹结构解析,在这种情况下温度和化学势都为0, 即T=μ=0,因此,G(p)应为以下形式:

G-1(p)=ipA(p2)+B(p2)

(5)

其中,A(p2)和B(p2)是p2的标量函数. 易得两式的解分别为A(p2)≡1和B(p2)≡M.代入PTR-2,推导得出:

(6)

把(6)代入能隙方程(3)

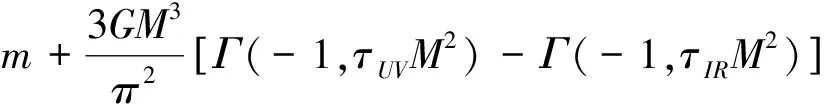
(7)

由(7)可以得到这个模型的4个参数:裸夸克质量m,耦合强度常数G,以及两个截断参量AUV和AIR. 因为AIR是为了模拟禁闭而被引入的,它的值应该根据核子半径的实验值进行修正. 本文采用AIR=235 MeV,以与半径实验数值0.84 fm相匹配[11].

(8)

将其代入能隙方程,得到M(T)

(9)

根据获得的M(T)关系,可以对不同的T给出数值解. 图1是根据表1所给出的3组参数而绘制的M(T)图像.

表1 文中所用的3组参数

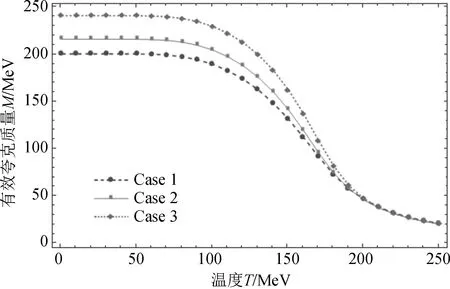
图1 有效夸克质量随温度的变化关系M(T)Fig.1 Effective quark mass M as a function of temperature T

从图1可以看出,曲线很明显地分为3段:低温段(0～50 MeV)、中温段(50～225 MeV)、高温段(>225 MeV),其分别代表不同的相,这与用格点QCD模型和其他模型方案所得的结果相一致[12-13]. 在低温段,夸克发生手征对称自发破缺,夸克获得有效质量,但没有发生相变;中温段是从夸克凝聚手征自发破缺到手征恢复的过渡,发生热核相变,有效质量急剧减小;在高温段,手征对称性恢复,相变完成,有效质量不再变化,根据Nambu-Goldstone 理论,如果此时m=0,则夸克有效质量M=0. 在非零化学势下,可以在中温段定义相变点(CEP),而在实验中如何找到这个点成为如今高能物理实验中十分重要的一个课题.

3 GMOR关系

在NJL模型中,π介子衰变常数可以通过真空到单π和轴向矢量电流矩阵元的Feynman图导出,如图2所示.

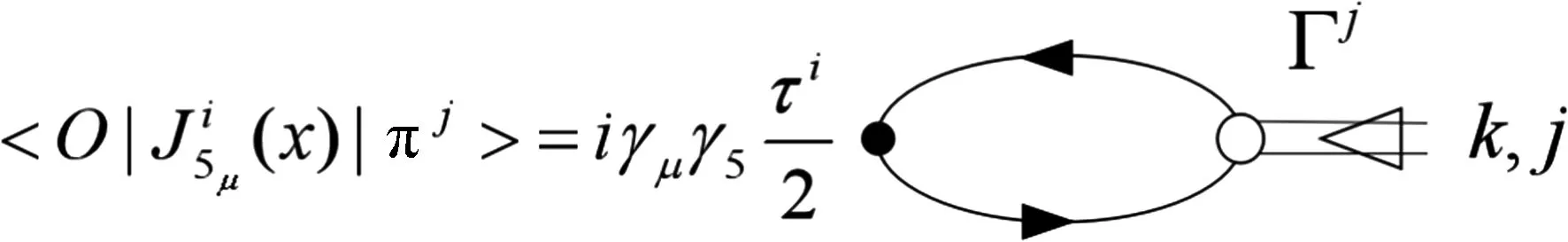
图2 真空到单π跃迁和轴向矢量流矩阵元的Feynman图Fig.2 Vacuum to one-pion and axial-vector current matrix element, as a Feynman diagram

对图2中的过程使用独立正则化方案,可以推出:

(10)

很多有效模型可以计算介子质量,比如手征夸克模型,Dyson-Schwinger 方法[14]以及弦模型[15]等. 在NJL模型,计算π介子质量有以下方程

(11)

其中

(12)

接下来讨论在该方案下的GMOR关系随温度的变化. 1968年,Gell-Mann, Oakes和Renner根据独立正则化方案的流代数结果导出关系式:

(13)

该等式的低阶近似在零温条件下成立,根据在NJL模型中运用正时正则化方案可以导出,在有限温下,该关系式各项都是T的函数. 对该关系式进行合理变形:

(14)

为了消除绝对误差对研究上带来的不便,根据百分偏差的定义,令:

(15)

为了方便对比,将M(T)进行归一化处理,定义相对有效夸克质量M1(T)

M1(T)=M(T)/M(T=0)

(16)

依据以上的推导及结果作出B(T)和M1(T)图像,见图3. 其中图像上部为3组M1(T)的关系,图像下部为3组B(T)的关系.

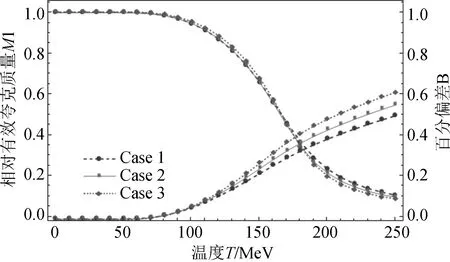
图3 GMOR关系式的百分偏差B和相对有效夸克质量M1随温度T的变化关系Fig.3 The percentage deviation of GMOR relation B and the relative effective quark mass M1 as a function of temperature T

对于GMOR关系式,低温条件下,在误差允许范围内,等式成立,但随着温度升高,在大于某一个阈值(50 MeV附近)时,曲线向上弯曲,说明此时凝聚值相对介子和衰变常数值乘积降低,等式不再成立. 通过对比B(T)和M1(T),可以看出,B(T)和M1(T)开始出现变化的起始温度几乎相同,说明GMOR等式的失效与凝聚变化有关,即与手征破缺恢复有关.

4 结 论

本文基于双味NJL模型,采用了正时正规化方案(PTR),推导了有限温下夸克凝聚随温度的变化,以及夸克凝聚时夸克质量随温度的变化,并研究了GMOR关系式在此条件下随温度变化的成立情况. 结果表明,在零温附近,GMOR等式在误差允许范围内成立,但随着温度的升高,超过某一界限(50 MeV附近)后,等式不再成立,且等式两边的偏差值越来越大.这是因为我们将关系式中涉及的有效耦合强度G视为常量,但更加深入的研究表明,我们似乎没有足够的证据这么做. 因此有足够的理由怀疑,在有限温条件下继续把有效耦合强度G视为常数并不合理,但至于G与什么因素有关且关系如何,还需要进一步研究和讨论.一些学者的最新研究表示G可能与温度有关,并试图探究两者之间的关系. 另外,在有限温有限密下可能存在多解,即南部解和维格纳解共存. 本文研究的只是南部解. 研究多解情况下GMOR关系的成立情况,也非常有意义,这对在高能实验中寻找相变点具有重要的指导作用.