基于工业电力大数据的GDP数据精准测算实证分析

曾 嘉，李 洁

（1．广东金融学院 国际教育学院，广州510521；2．深圳大学 中国经济特区研究中心，广东 深圳518060）

一、研究背景

长期以来，政府政策的制定和实施始终以宏观经济发展趋势为基本参考，并根据这些预测趋势对现有政策体制作出针对性的调整。但学术界对于提升GDP数据频率而提出的大部分方法都是以及时获得宏观GDP数据为基础条件，具有一定的局限性。而估测模型中往往存在投资指数、经济周期变化等因素，模型的准确性难以保证，运用这些方法进行GDP估测存在滞后性。然而，与宏观经济数据不同，一些工业数据在数据总量和计算时间上具有天然优势，具备相当的及时性和可靠性，并且可以从不同角度反映其与宏观经济之间的具体关系，因此学术界逐渐将焦点放在此类数据的研究上，其中电力大数据的发展与利用逐渐成为中国学者们关注与研究的焦点之一。

二、文献综述

中国学者对GDP的估测进行了很多有益研究。唐成千和莫旋（2016）结合中国经济周期性波动的实际数据，通过构建混合频率数据抽样模型，对中国宏观经济进行了探讨和短期预测［1］。索泽辉和冼军（2015）将Lomb-Scargle周期图法运用到GDP的预测中，并建立了Lomb-Scargle周期图法的指数预测模型，从而明显提高了预测精度［2］。杨利雄和张春丽（2018）以组合预测理论、无偏性和有效性检验以及时域—频域分析为基础，对中国季度GDP初步核算数据的准确度进行了评估［3］。张劲帆和刚健华（2018）等人利用中国宏观经济指标构建了基于贝叶斯估计的混合频率向量自回归模型，同时利用该模型检验了中国宏观经济的运行情况［4］。杨少文和熊启泉（2014）提出了以GDP份额预测经济开放程度的研究方法，并对中国1994—2011年期间的各年度经济开放度进行测算，其实证结果较好地反映了中国经济的变动情况［5］。仝冰（2017）利用DSGE模型对GDP数据进行贝叶斯估计，发现参数估计结果出现了系统性偏差，而使用年度的支出法消费和投资数据进行估计，则模型的样本外预测绩效总体更优［6］。

对于电力大数据与宏观经济之间的关系，近年学术界也展开了激烈的讨论。冯永晟（2014）利用微观数据研究得出了中国居民的长期电力需求函数，并指出了其与宏观经济的波动联系，为居民电价政策评估提供了基础依据［7］。潘竟虎和李俊峰（2016）以中国大陆为研究对象，从不同时间、空间角度对省级、地级和县级单元的电力消耗量变化趋势和空间集聚程度进行了分析，这在一定程度上反映了不同地区的宏观经济情况［8］。

根据上文可知，工业电力大数据与GDP联系紧密，表明电力大数据与GDP之间存在正向关系方程，根据正向关系方程倒向解构，即利用参数估计值反向倒推，便可实现对宏观GDP数据的估测，并且最终根据本研究所得结果亦可反验证此方法的科学性和有效性。本研究所用倒向回归方程由正向回归方程解构而来，研究分以下几步：第一，说明对电力数据的基本处理方式，以此提升可得数据的有效性和准确性；第二，以江苏省工业电力大数据为基础，运用渐次回归逐步构建电量与GDP增长率的方程，并引入与GDP有关联的影响因子，建立倒向回归模型；第三，考虑到不同地区和时间的产业特征，通过设定窗口期对模型因子进行动态调整，提升GDP测算的准度和精度，最终得出研究结论。

三、理论说明与模型构建

最小平方法（OLS法），采用最小化误差的平方方式寻找数据的最佳函数匹配。本研究使用OLS法进行渐次回归，构建工业企业用电量与GDP增长率等变量关系的线性公式：

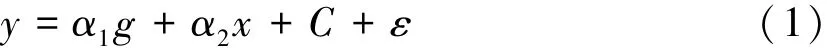
公式（1）中，y代表工业用电量增长率，g表示GDP的增长率，x为其他自变量。

以（1）式为结构基础，利用倒向回归推导出g关于y的方程，通过频率较高和及时性特征的工业用电大数据进行方程推导，可消除GDP估测的时滞性并提升频率。并在推导出的倒向公式中，引入高频率的工业企业用电量数据来构建关于宏观经济增长率的测算模型。即将影响因子和异频工业企业用电量增长率的真实数据代入所得方程，以此获得当下时间区间的g的估测结果。在此通过以下几步进行模型构建：

首先，在回归方程中代入自变量和因变量。

基于前文说明，在此使用因变量为工业企业用电量增长率yt，自变量为GDP增长率gt。则式（2）为代入时间t的工业企业用电量增长率的计算方程，式（3）为代入时间t的GDP增长率的计算方程。

将影响工业企业用电量的影响因子代入基础方程中，由于影响工业企业用电量的因素有很多，根据学术界普遍认同的工业电力数据的影响因素，在此选取季度气温的平均涨幅、PPI增长率、产业发展程度、城镇人口增减幅度和相关虚拟变量作为控制变量。

其中，PPI指数在一定程度上反映特定时间内生产环境的价格升降状况，在国民经济领域中是必不可少的指数依据。根据电力用量与PPI的相互关系［9］，在此用 pt表示t时间的 PPI指数，式（4）为代入时间t的计算公式。

产业发展程度It表示了各产业在国民经济中贡献GDP的多少。由于各产业的特性和发展差异，不同产业的企业用电量增速有明显差异。而城镇人口增减幅度Rt会对产业的人员数量产生影响，与产业规模和产业用电量有关。因此，将产业发展程度和城镇人口增减幅度作为影响因子，即作为因变量代入倒向方程。

由于产业生产环境和家居环境的制约，气温的平均上升程度与用电量有着天然的联系，相关研究认为平均气温与用电量显著相关［10］，且由于季节性的气温差异，用电量和平均气温的关系呈现显著的周期性变化。因此，以当季度气温的平均上升程度wt作为控制变量，并加入温度相关的虚拟变量，即高温季WH和低温季WL。若此季度为高温季，则有WH=1；若为非高温季，则有WH=0。若此季度为低温季，则有WL=1；若为非低温季，则有WL=0。通常的高温季为一年中的第三季度，低温季为一年中的第一季度。式（5）为温度的平均上升程度的计算公式。

对于工业企业用电量，必须考虑节假日的影响。例如春节、十一国庆等长假期间，企业用电量会大幅缩减，长假结束后的设备启用也需要一段时间，因此引入季度内的节假日时间变量Jt与假期相关的虚拟变量JS。若季度内存在5天以上假期，则有JS=1；若季度内不存在5天以上假期，则有JS=0。

由于官方的相关数据大部分为每季度公布一次，因此本研究大部分变量以季度为单位，其中PPI和城镇人口增减幅度以年度为单位。表1为变量说明，其中包含自变量、因变量、控制变量和虚拟变量。

表1 变量说明

将各变量代入，则有：

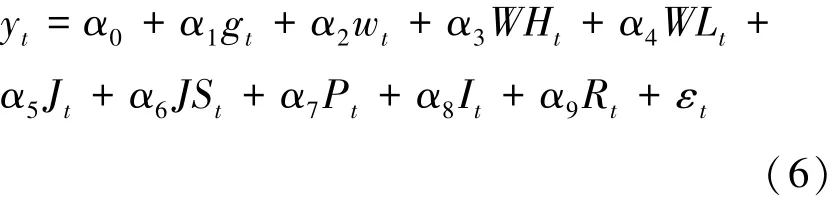
上式中的变量数据获得以季度为单位，其中由于Pt和Rt这两个变量的公布频率以年为单位，在此为了便于计算，设定这两个变量数据在一年的期间内变化幅度为平均上升或平均下降，在代入公式的过程中，以年度幅度的四分之一作为季度内的有效数据。

然后，运用渐次回归方式进行参数因子估计，并检验最初变量的回归系数，即α1-α9，从中选出显著影响工业企业用电量数据的相关变量。在（6）式中，包括初始参数α0及9个变量的回归参数，运用经济学软件MATLAB进行OLS估计，得到回归系数的具体估计数值α0-α9，再对各变量分别检验，以决定该变量是否应被引入模型中，理论上剔除影响并不显著的变量，进而确定最终的回归方程。

本研究的目的是利用工业企业用电量数据的及时性与高频率等特性，测算宏观经济增长的数据，即由方程（6）倒向回归构建出GDP增长率与工业企业用电量的关系方程，进而估计得到高频率的GDP数据。最终的回归方程如下：

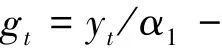
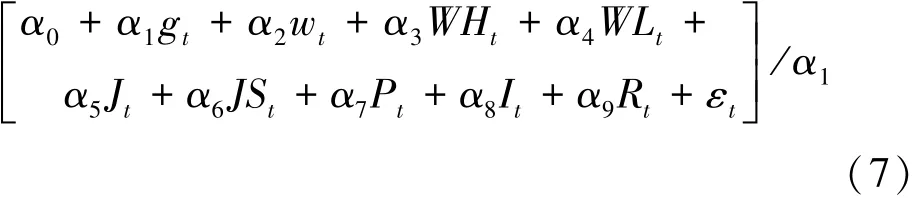
由上式可得，GDP增长率的估测数据gt是在工业企业用电量增长率与其回归系数α1之比的基础上，通过保留非显著影响因素而得到的，因此可以通过工业企业用电量增长率及一些重要影响变量，倒向解构得到高频GDP的增长率。

四、实证研究——以江苏省工业电力大数据为例

（一）实验数据的采集说明

本研究采集2007—2018年12年内每个季度的江苏省工业电力数据、省内GDP、平均温度、假期天数、PPI指数、城镇人口数量和产业发展程度数据进行分析。其中，省内温度数据来自江苏省气象局；GDP及PPI等数据来自中经数据库；其他数据如江苏省工业用电量，从江苏省供电系统网站采集取得，由官方数据抽调并整合。

工业企业用电信息采集平台需要对工业企业电量数据进行一定的数据集成，通常包括收集、存储和剔除整合等处理步骤。电力企业利用光纤网络将采集到的数据由集成器输送到中央主控系统，频率为6次／分，最大程度地消除数据滞后现象。主控系统通过数据的分散存储，将数据转移到主控系统下的分设备内储存，形成各个分散的小数据库，使数据得到高效率运算。分系统会自动识别重复和无意义的非工业企业数据，实现相关数据的挖掘整合，为最终的回归分析打下基础。利用Golden Gate对平台的基础数据进行提取，存储到多个分块节点内，在各分块储存器内部进行一定的计算和剔除，将各分块储存器的最终数据整合到MapReduce中进行高级运算，并对数据进行相关排序，最终得到2007—2018年的工业企业电力数据，其数据趋势如图1。

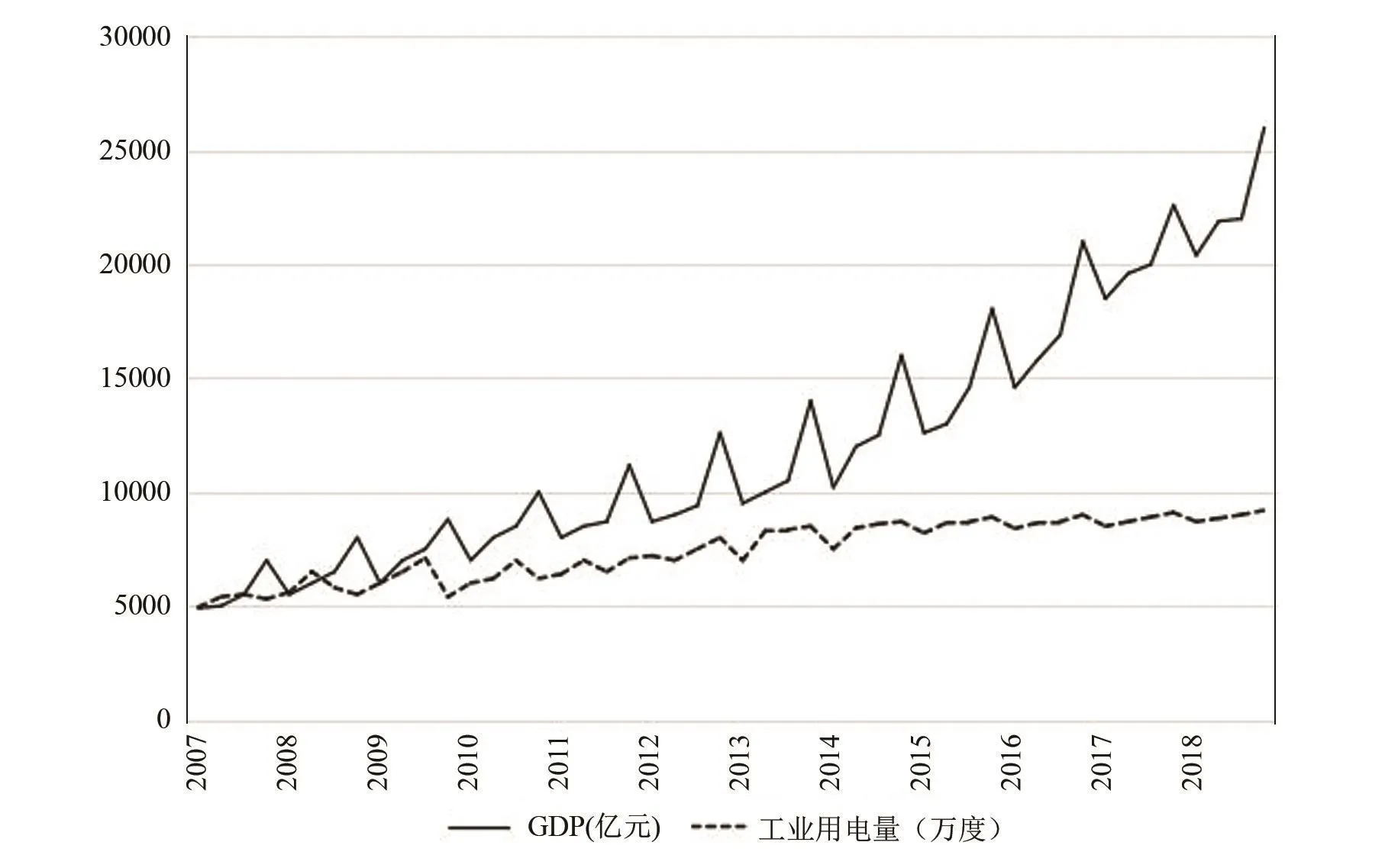
图1 2007—2018年江苏省工业用电量和GDP的季度趋势

根据图1，可以得出江苏省的工业用电量及GDP数据总体上呈现上升趋势，其中工业用电量的平均年增长率为2．31%，GDP的平均季度增长率为4．25%。江苏省工业用电量的增长速度相对缓慢，GDP的增长幅度则逐步提升，这表明GDP与工业企业用电量之间并非单纯的相互影响，两者在交互影响中也受到其他影响因素的作用。

（二）数据平稳性检验

为了确保数据的可用性和有效性，有必要对数据进行平稳性检验。在此用扩展的迪克富勒检验方法（ADF）对江苏省工业企业用电量和季度GDP的时间序列进行稳定程度检验。这两个时间序列取ln值，分别用Ly和Lg表示；对Ly和Lg进行ADF检验，根据结果判断这两个序列的稳定性，表2为ADF检验结果。

由表2可得知，Ly和Lg的时间原始序列的t统计量概率值大于0．05，表明两个原始时间序列不具备平稳性。但是ΔLy和ΔLg的t统计量概率值为0，证明两个原始序列的一阶差分序列具备稳定性，即工业用电量增长率和GDP增长率的时间序列具备稳定性。可得出结论，GDP的增长率比GDP数据本身更具备估测价值，因此对增长率进行回归分析具备可靠性和有效性。

日尼神山脚下，村庄依着山势次第摊开。幽蓝的炊烟下，民舍和庄稼才刚被雨水清洗过，在正午的阳光下分外清丽。

表2 ADF检验结果

（三）渐次回归并剔除非重点变量

对工业企业用电量增长率和GDP增长率两个序列进行渐次回归，并在回归过程中对其他控制变量进行观测筛选，剔除影响不显著的变量，最终使模型的结构达到最优。利用Matlab对变量进行OLS回归，最终得到10个回归系数。利用显著性区分法，去掉P值最高的回归系数的对应变量，保留其他变量，再重复进行此操作，对剩余变量进行渐次筛选，最终得到自变量显著效果最佳且对应度最高的模型。

通过利用Matlab的逐步OLS回归，发现工业用电量增长率的二阶滞后自相关性较高，在（6）式引入y的滞后参数，即yt-2，得到回归方程：

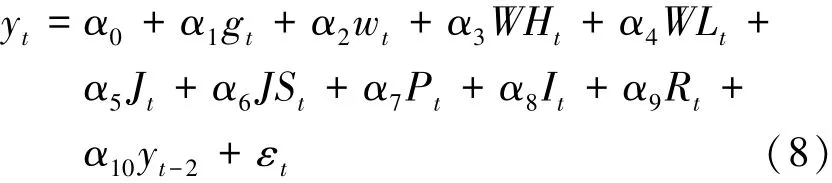
对（8）式采用最小二乘法回归，得到季度内温度的平均上升程度wt的回归系数P值最高，为0．980；去除季度内的气温平均上升程度变量，再对其余的变量进行回归，逐步去除低温季WL和高温季WH。由于去掉的变量均与气温相关，由此可知气温对工业企业的生产较难产生显著影响；温度浮动与工业企业用电行为并不显著相关，其对用电量的影响作用体现在家庭的个人行为。经过渐次回归，得到的自变量和保留的控制变量均影响显著。表3为渐次回归过程结果。

表3 渐次回归过程结果

在保留影响显著的变量后，得到下式：

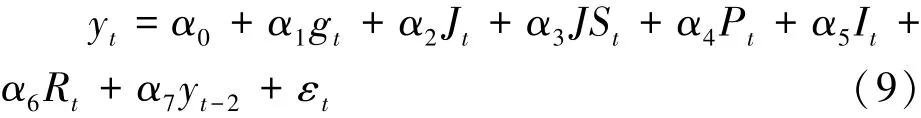
以江苏省 2007—2018年的工业用电量及GDP数据为基础对（9）式进行正向回归，表4为正向回归结果。

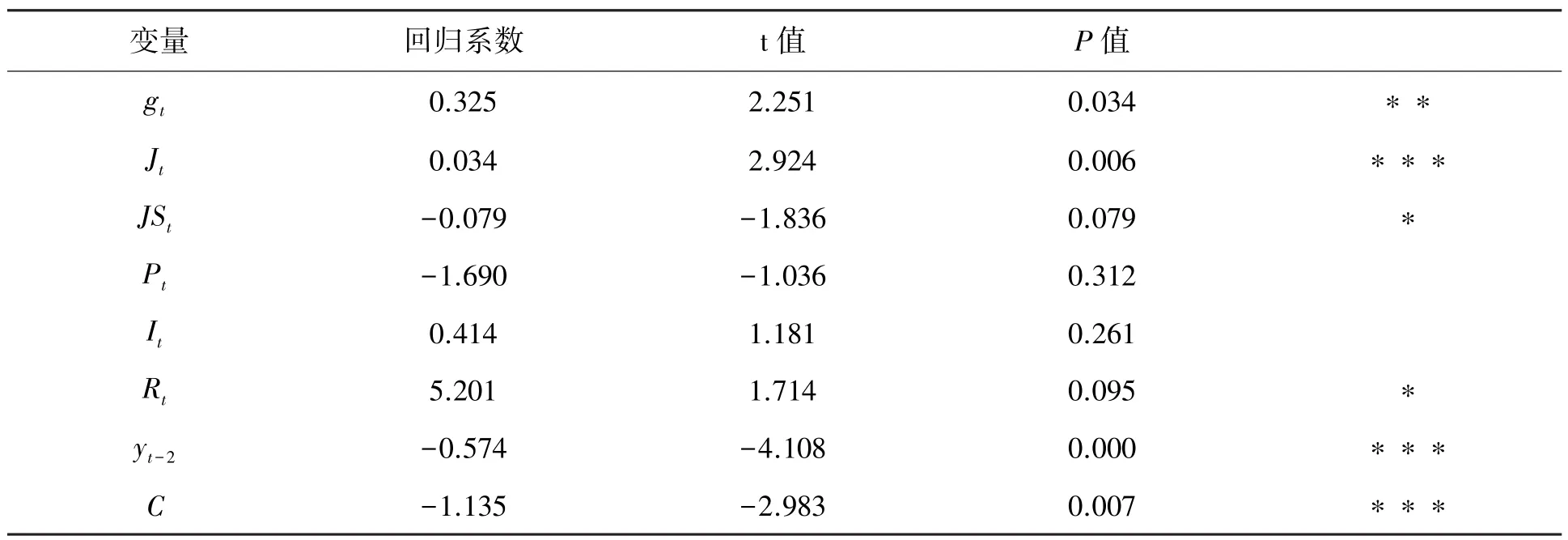
表4 正向回归结果

将表4的所得的回归系数结果代入（9）式，获得GDP增长率的估测方程：

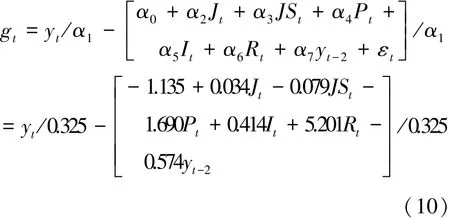
而针对GDP的数值估测，可由下式获得：

（四）根据电力数据实现季度GDP的增长率测度

上文得到的模型方程是在回归系数长期维持不变的基础上获得的，但随着时间线延长，宏观经济状况与工业用电之间的具体作用会根据产业发展状况的变化有着相应的动态调整，因此回归系数并不是一成不变的。为了提升GDP数值的准确度，本研究通过设定窗口期，在动态中实现模型的拟合回归。

本研究选用的数据时间跨度为12年，每年包括4个季度，通常来说，3年内的经济状况和技术革新情况相对而言不会产生显著变化，在此将窗口期的时间跨度定义为10个单位季度，先对初始窗口期的数据进行参数估计，将估计结果作为下个时间期的GDP增速测度基础，到下个时间期的时候，将窗口向后推移，删除最初的季度数据，增加后一个新季度数据，因此窗口期的时间季度始终维持在特定值。以此类推，通过窗口期的渐次移动，最终构建出测算GDP的动态测度模型，即根据特定窗口期时间的非固定参数构建模型。

由于使用的用电量数据迟滞一个季度，季度样本共43个，窗口期为滚动的10个样本，在此正向方程的回归过程共33次。抽取2011年一季度至2018年二季度的所有点位进行GDP测度，并将测度结果与官方公布的实际值进行对比。图2为官方GDP增速数据与GDP增速测度结果的趋势对比，图3为官方GDP数值与GDP测度结果的趋势对比，可得出官方数据与测度结果的拟合程度。

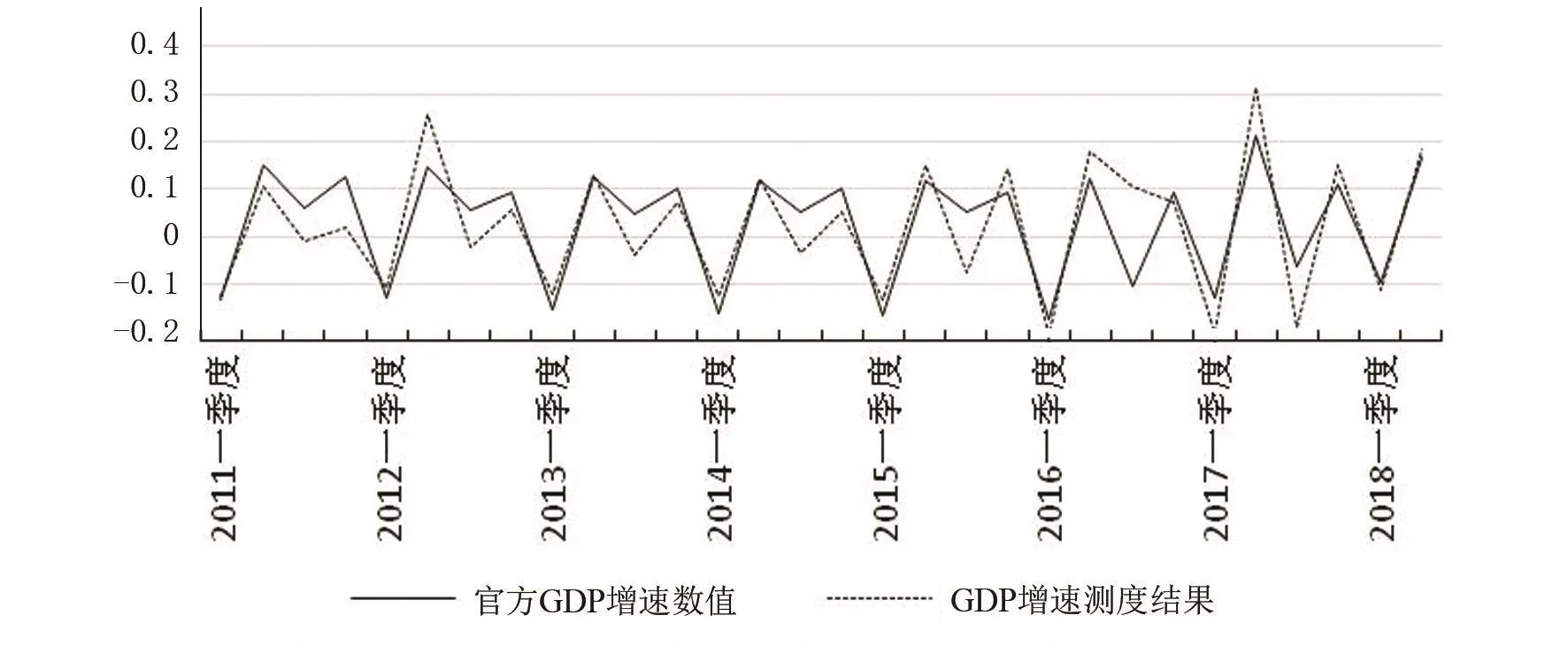
图2 官方GDP增速数据与GDP增速测度结果的趋势对比

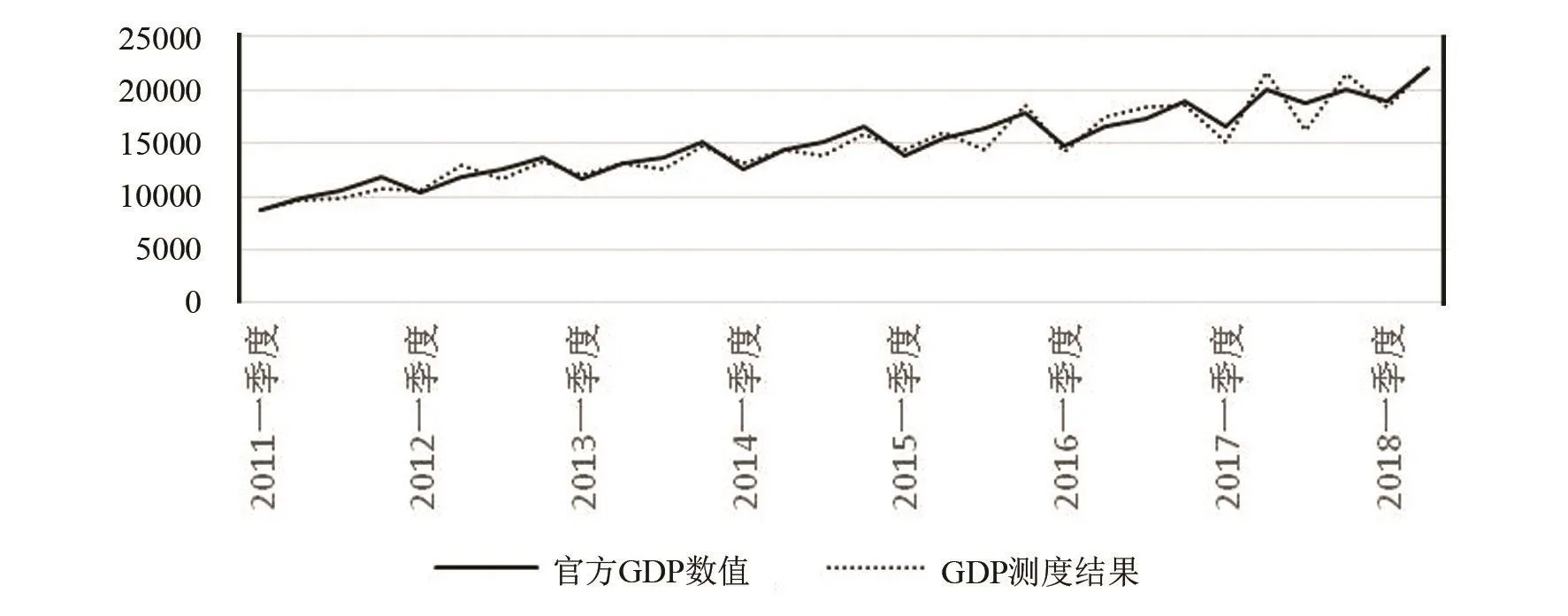
图3 官方GDP数值与GDP测度结果的趋势对比

倒向回归得到的GDP增速与官方公布的GDP增速数值在符号上保持一致，且两者的趋势差异较小，拟合程度较高。拟合程度最接近的是2012年第四季度，差值百分比为0．30%。图2和图3更加明显地反映了两者之间的拟合程度。图2中2011年一季度到2018年第二季度期间，GDP增长率的估测结果与官方数值趋势整体相同、整体差异较小，证实了本文使用的通过工业企业用电量数据倒向测度GDP增速的方式是可靠有效的，测度数值的拟合程度较高。

（五）根据电力数据实现年度GDP增速的测度

以上文得到的季度GDP增速的测度结果为基础，估测2011—2017年间的年度 GDP增速。将测度结果与官方公布的实际值进行对比，图4（见下页）为官方年度GDP数值与年度GDP测度结果的趋势对比。

图4 官方年度GDP数值与年度GDP测度结果的趋势对比

可以看出，年度估测结果与季度估测结果相比，与官方给出的数据拟合程度更高，差异更小，且年度测度结果与官方数值的平均误差在2%以下，说明得到的年度估测结果一定程度上消除了季度估测的偏离差异，使得年度估测与官方实际数据的拟合程度更高。由图4可看出，年度测度结果与官方实际数据之间的拟合波动较小，其偏差程度要优于季度估测趋势对比，这再次证明了本研究使用的倒向解构测度方法的可靠性，不仅可有效提升GDP频率，还在消除滞后性的同时缩小了测度数与官方数据的拟合差距。

（六）用工业电力大数据测度高频GDP增速

现实中往往需要更高频率的以月度甚至周为单位的GDP数据。在此对江苏省每天的工业企业用电量数据进行收集并处理，代入上文模型，估测出每天的GDP增速，在此基础上进而估测得到月度乃至周度的GDP增速，并估测出月度GDP和周度GDP的具体数值。利用2013—2017年的实际数据估测得到的日度GDP增速来倒推季度和年度的GDP增速，并将其与公布的实际数据进行趋势对比。图5为季度GDP实际增速与GDP增速估测结果的对比，图6为年度GDP实际增速与GDP增速估测结果的对比。

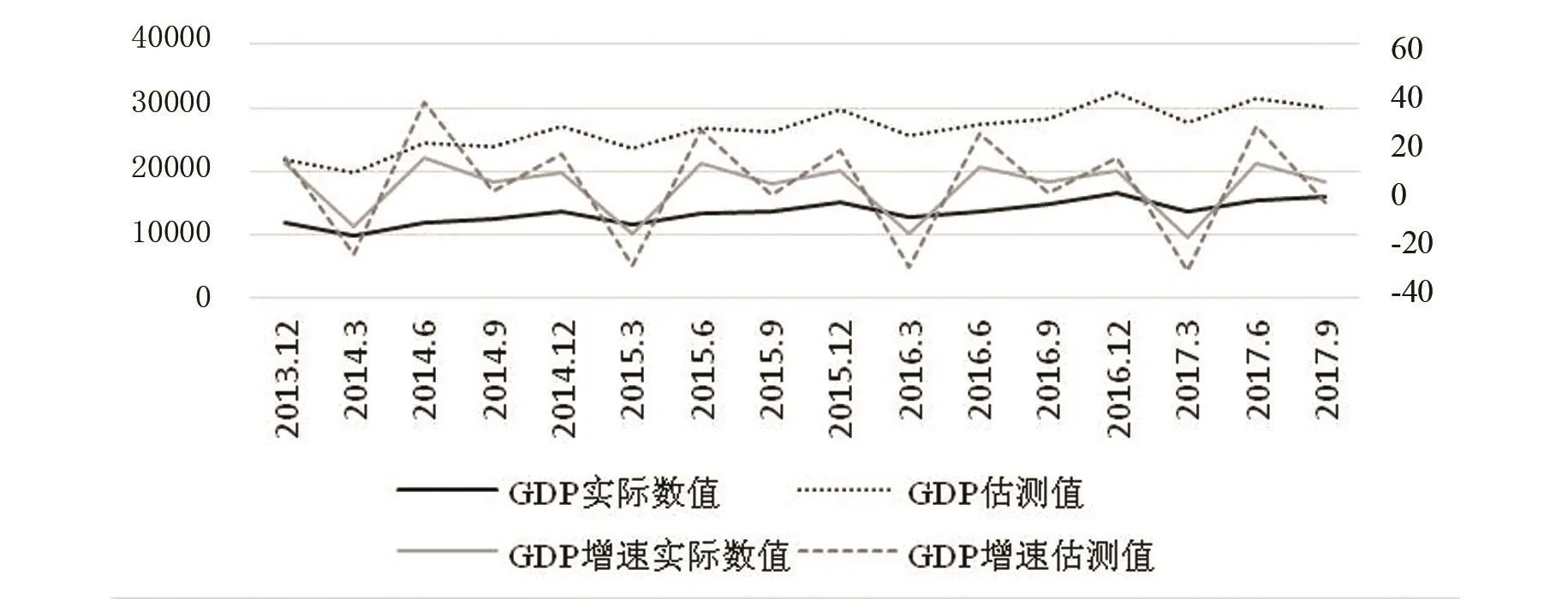
图5 江苏省季度GDP实际增速与GDP增速估测结果的对比

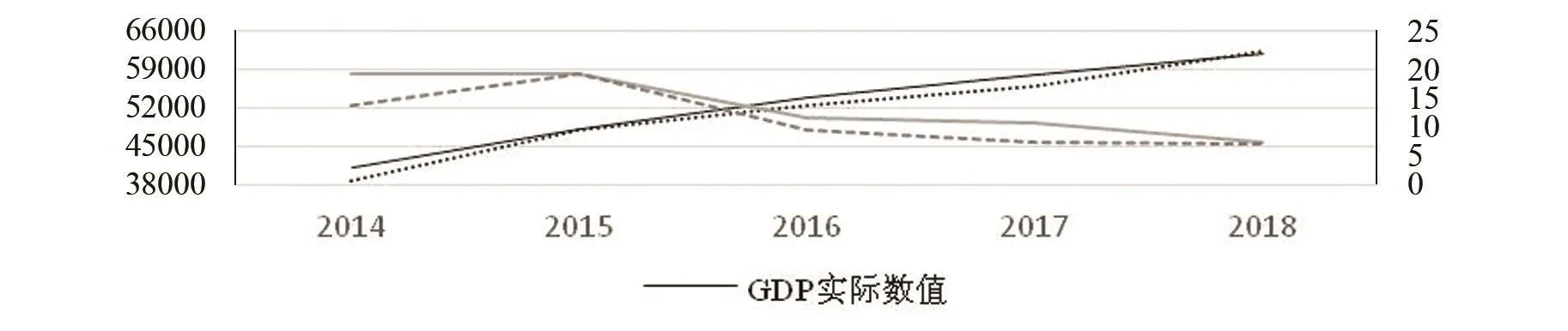
图6 江苏省年度GDP实际增速与GDP增速估测结果的对比

根据图5及图6，可得出基于工业电力数据估测得出的季度及年度GDP增速和数值均与实际数据深度拟合，且拟合差异较小，甚至在2015年度GDP估测值与官方数据趋于一致。将年度数据与季度数据作对比，就GDP增速和数值来看，年度数据的拟合状况更优于季度数据。因此得出结论，根据工业电力大数据估测出的不同频率的GDP数值，其趋势走向及数值均与实际数值较为接近，表明本文采用的方法可以实现对宏观经济可行且可靠的预测。

总 结

本文基于工业电力大数据，通过构建动态倒向回归方程，实现对GDP数据的精准测算。通过对2007—2018年间的电力数据进行估测，发现无论基于季度还是年度的时间区间，利用倒向回归得到的GDP增速均与官方公布的GDP增速数值在符号上保持一致，且两者的趋势差异较小，拟合程度较高，表明利用江苏省的工业电力大数据可以实现当期省内GDP的增速估测，且利用此方法对宏观经济进行预测是可行且可靠的。而由于电力数据平台的完备与及时性，较容易得到月度、周度乃至日度的电力大数据，再通过倒向构建回归方程即能估测出更高频率的GDP数值，进而能大幅提升政府、企业团体及公民个人的金融规划效率。

本文的创新之处在于，利用工业电力数据的及时性和高频特性，通过倒向回归方程实现对GDP的精准预测，在很大程度上突破了GDP数据的低频和时滞约束。同时，通过对原始数据的耦合和分散处理，尽量避免了由于数据样本偏差影响测度结果精准度的情况，并且通过设置固定时间周期的窗口期，实现了回归模型参数在非固定时间周期内的动态变化。