CO:LiCl(001)-(1X1)表面电子激发态及其随时演化
陈武超, 王能平
CO:LiCl(001)-(1X1)表面电子激发态及其随时演化
陈武超, 王能平*
(宁波大学 物理科学与技术学院, 浙江 宁波 315211)
采用多体摄动理论研究CO:LiCl(001)-(1X1)表面的激发态性质、CO分子激子态随时演化及其寿命. 首先用局域密度近似的密度泛函理论计算CO分子吸附在LiCl(001)-(1X1)表面的几何结构; 随后运用GW近似研究LiCl块体、LiCl(001)-(1X1)干净表面以及CO:LiCl(001)-(1X1)表面的准粒子能带结构, 引入电子-空穴相互作用, 求解二粒子格林函数的Bethe-Salpeter方程(BS方程), 并得出其电子-空穴激发态及光学吸收谱, 将计算得到的光吸收谱与实验数据进行比较; 最后基于吸附系统CO:LiCl(001)-(1X1)的BS方程的解, 求解含时薛定谔方程得出的分子激发态的随时演化. 因衬底和吸附分子之间的耦合作用, CO分子激子态在随时演化的初始阶段呈现非常快的衰减, 其寿命仅为0.75fs. CO分子激子态的空穴大幅度地向衬底转移, 而激子态的电子仍然滞留在CO分子上.
准粒子能带结构; GW近似; 电子激发态; BS方程; 随时演化
电子激发态及其随时演化的特性在物理和化学领域有着重要的应用[1-3]. 描述电子激发态衰变的重要物理量之一是电子激发态的寿命, 电子激发态的寿命决定于电子与其他准粒子之间的相互作用, 如单粒子激发的电子、空穴, 以及集体激发的声子、磁振子、等离子体振子等. 在实验中光电子能谱[4-6]可通过测量谱线形状和线宽占据态的衰变研究, 反光电子能谱[7-8]、双光子光电子能谱[9]和时间分辨[10-11]可测量非占据态谱线形状和线宽研究其衰变特性. 在理论上多体理论被用于研究金属中电子和空穴的动力学性质. Hedin等[12-13]研究的GW近似被广泛用来计算电子-电子散射对普通金属(顺磁介质)中单粒子态衰变率[14-15]. 但对于铁磁金属, 精确的计算需要考虑GW+T矩阵近似[16-17].
原子(或分子)吸附于金属表面电子激发态的衰变[14,18-22],以及吸附原子(或分子)上瞬时激发态的随时演化[23-28]研究表明: 一方面衬底表面的电子因受到吸附分子的散射, 衬底表面的电子激发态将发生衰变; 另一方面吸附分子上的电子也受到衬底的作用导致吸附分子上激发的电子或空穴转移到衬底上. 通常化学性质活泼的衬底和吸附分子之间的强键会导致单粒子态的较快衰减. 而绝缘体衬底因化学性质较惰性, 其电子与吸附分子上的电子之间不易发生共振, 阻碍了电子由分子跃迁到衬底, 因此限制了分子上单电子(空穴)态的衰减. 然而, 本研究发现, 即使分子上的单电子态的衰变被禁止, 这种阻碍对分子激子态的衰变并不存在; 对于CO吸附在LiCl(001)-(1X1)表面的情形, CO分子激发态的随时演化过程是一种在飞秒尺度范围内极速的二粒子态衰变过程.
电子激发态动力学性质的研究依赖于对系统电子能带结构的精确计算, 对激子态的随时演化探讨也有赖于电子-空穴激发能谱的精确计算. 对多粒子系统, 局域密度近似(LDA)的密度泛函理论(DFT)已被证明是计算基态性质的有效方法[29-32], 利用该方法可得到系统的基态几何结构的可靠结果. 但是, 局域密度近似的密度泛函理论严重低估了半导体和绝缘体的带隙. 准粒子能带结构的精确计算方法是GW近似[12-13]. GW近似理论的突出特征是引入了非局域、能量相关的自能算符(该算符是单电子格林函数和动力学屏蔽的库仑相互作用的卷积), 以改进局域密度近似对电子交换关联的处理[30-31,33-36]. 半导体和绝缘体的光激发受到电子-空穴相互作用的影响, 而该作用不能简单地用独立粒子图像来描述. 光激发的精确计算需要运用把电子-空穴相互作用考虑在内的二粒子格林函数方法, 求解二粒子格林函数的运动方程, 即Bethe-Salpeter方程(BS方程)[37-38], 进而得到电子-空穴激发态和光学吸收谱[30,33-35,39]. 文献[40]报道了关于分子吸附在半导体表面的电子激发态衰变, 但有关分子吸附于绝缘体表面的电子激发态的随时演化研究较为鲜见. 目前还未见有关于CO吸附在LiCl表面的电子激发态随时演化的研究报道.
本研究利用局域密度近似的密度泛函理论, 计算了CO分子吸附于LiCl(001)-(1X1)表面的几何结构; 并运用GW近似, 计算系统的准粒子能带结构. 引入电子-空穴相互作用, 求解了二粒子格林函数的BS方程, 进而计算光吸收谱. 在此基础上, 求解含时薛定谔方程, 研究了CO分子激子态的随时演化.
1 计算理论方法
1.1 电子基态性质
分子和晶体的基态性质可以用密度泛函理论来描述[41-42], 在局域密度近似下可得有效的哈密顿本征方程, 即KS(Kohn-Sham)方程[42]:
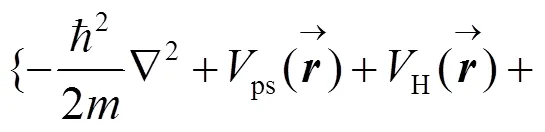

本文采用Hamann模守恒赝势[44], 对于Li的赝势, Li的1s态和2s态都纳入价带中; 对于Cl的赝势, 与通常处理方法一样, 仅将Cl的3s和3p态作为价电子态. 以高斯函数为基函数, 将局域密度近似密度泛函理论的波函数表示为高斯基函数的线性组合[45]. 高斯基函数都含有s, p, d, s*这4个轨道, 其中Li的衰减常数为0.15、0.50、1.80和6.00; Cl的衰减常数为0.20、0.60、1.20和3.60; C的衰减常数为0.15、0.67和3.00; O的衰减常数为0.25、1.00和3.70. 高斯基函数也应用文中GW自能运算.
1.2 准粒子能带结构
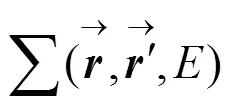
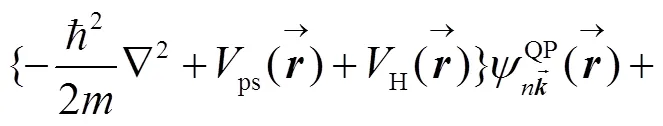
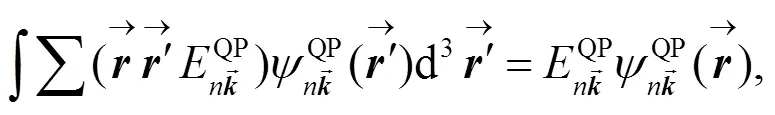
GW近似的自能算符定义为[12-13]:
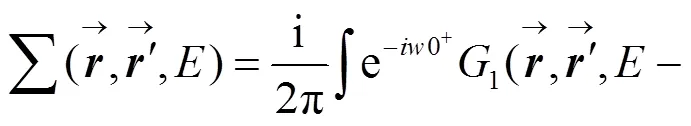


1.3 光致电子激发态
虽然GW近似可精确计算半导体和绝缘体的准粒子能带结构, 但由于光激发过程中存在电子-空穴相互作用, GW近似的独立粒子物理图像不能描述光致电子激发态, 即电子-空穴激发态. 光致电子激发态可用二粒子格林函数理论来描述. 在Tamm-Dancoff近似下, 光致激发态波函数可表示为[37-38]:




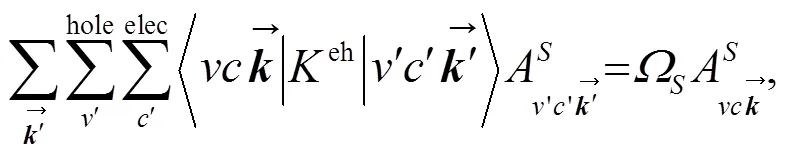


在忽略电子-空穴相互作用的情况下, 宏观横向介电函数的虚部可近似地写为:

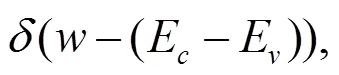
1.4 电子-空穴激发态的随时演化
对于CO:LiCl(001)-(1X1)表面, 含时薛定谔方程可写为:
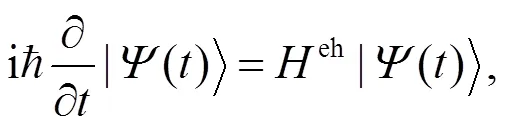
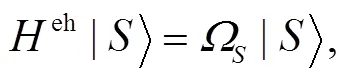
含时薛定谔方程(8)的形式解为:
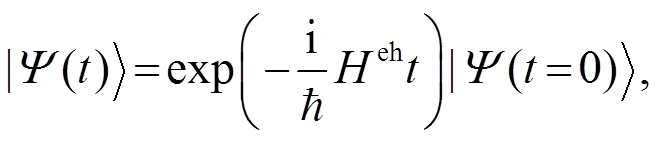
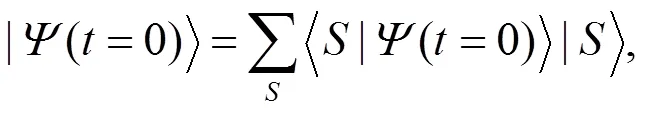

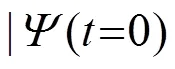
2 LiCl块体及LiCl(001)-(1X1)干净表面的电子激发
LiCl块体具有岩盐结构, 运用局域密度近似的密度泛函理论计算其基态能量, 分析基态能量对晶体结构常数的依赖关系, 得出基态能量最低时的晶体结构常数为0.503nm. 该理论值接近其晶格常数的实验值0.513nm, 相对偏差仅为2%. 为了与实验结果相比较, 在后面计算中均采用实验晶体结构常数.
通过自洽迭代求解KS方程, 计算空间布里渊区高对称点的本征能量, 可获得电子的本征能量与波矢的关系, 即能带结构. LiCl的价带包括Li 1s带, Cl的3s和3p带, 局域密度近似的能带结构见图1. 从图1可知, 最低的导带主要是Li 2s轨道的贡献(包括很少的Cl元素轨道的贡献), 最低的导带被近似地标为Li 2s. LiCl具有-直接带隙5.9 eV. 关于带隙, 局域密度近似的密度泛函理论结果明显低于实验测量值9.4eV[47].
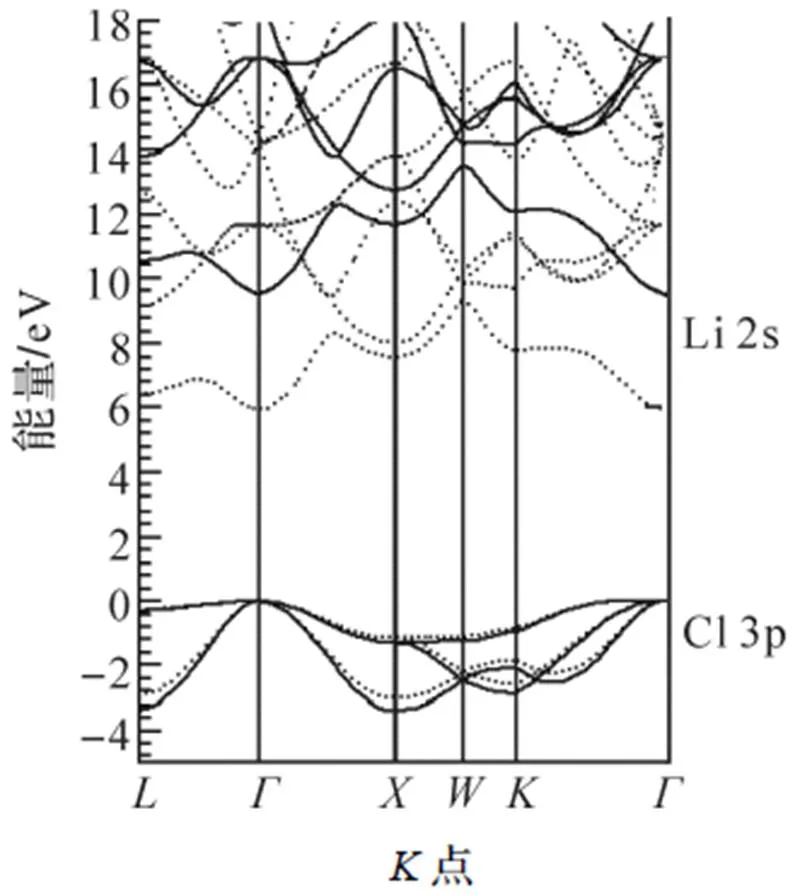
图1 LiCl块体的局域密度近似能带结构(点线)与GW近似能带结构(实线)
基于局域密度近似的密度泛函理论的计算结果, 运用GW近似求解方程(2), 计算空间布里渊区高对称点的本征能量, 可得GW准粒子能带结构(图1中实线). GW近似的-直接带隙是9.5eV, 与实验结果9.4eV[47]相符. 另外, 在局域密度近似下, Cl 3p带和Li 2s带的宽度约为3.0eV和3.3eV, 而在GW近似下其宽度分别增加到3.4eV和4.1eV. GW近似下, Cl 3s带位于-14~-13eV之间, Li 1s带位于-52eV. Li 1s带和Cl 3s带能量太低, 为提高能带图的清晰度, 这2个价带未在图1中显示.
利用GW近似的理论结果, 并引入电子-空穴相互作用, 求解方程(5), 可得到光致激发态的激发能和波函数; 再运用式(6), 可计算得出光吸收谱. 在运算中考虑了Cl的3s和3p价带, 以及9个最低的导带; 因Li 1s能带太低, 其对激发能不高于13eV范围的光吸收谱的影响可忽略, 故在运算中未考虑.空间布里渊区内取500个点, 计算得到LiCl光吸收谱(图2(a)中实线). 此外, 通过尝试增加导带的数量或增加点的数目展开计算, 发现在不大于13eV的较低激发能范围内, 所得到的LiCl光学吸收谱保持一致, 表明所纳入计算的能带数量和点数目对于所求的光学吸收图谱已满足收敛性要求. 光吸收谱的第1个吸收峰位于8.85eV的激发能处, 是最低的激子态, 其激发能比准粒子带隙约低0.65eV, 即最低激发态的束缚能为0.65eV. 2个吸收峰位于激发能为9.75eV 处, 该吸收峰的激发能大于准粒子带隙, 所对应的激发态不是真正的激子态, 而是共振激子态.

图2 LiCl块体的光吸收谱
LiCl光吸收谱的实验结果[48]见图2中点线. 从图2(a)可看出, 在GW近似基础上引入电子-空穴相互作用, 并由二粒子格林函数理论计算得出的数值结果与实验结果相符, 理论结果能较好地再现实验所观测到的两大吸收峰和曲线的基本走势.为了分析电子-空穴相互作用对LiCl光吸收谱的影响, 在GW近似的准粒子能带结构和波函数结果的基础上忽略电子-空穴相互作用, 利用式(7)计算独立粒子近似的光吸收谱(图2(b)中点划线). 文献[49]利用局域密度近似的密度泛函理论所得出的能带结构和波函数, 并忽略电子-空穴相互作用, 得出了LiCl光吸收谱(图2(b)中长虚线). 本文利用GW近似所得的独立粒子光吸收谱的吸收边比文献[49]利用局域密度近似得到的独立粒子光吸收谱的吸收边约高3.8eV, 这是因为局域密度近似严重低估了LiCl的带隙所致. 但这2个独立粒子近似的光吸收谱在吸收边附近都无强吸收峰, 与实验结果[48]偏离很大, 所以LiCl中的电子-空穴相互作用对光吸收谱的影响显著, 必须考虑.
对LiCl(001)-(1X1)干净表面, 采用包含6层原子和1.2nm厚真空层的周期性超晶胞, 利用局域密度近似的密度泛函理论, 计算表面原子受力并优化LiCl(001)-(1X1)表面的几何结构, 发现表面原子的弛豫幅度很小, Li原子向里弛豫0.005nm, Cl原子向外弛豫0.003nm.
对驰豫后的LiCl(001)-(1X1)表面, 利用局域密度近似计算表面的能带结构(图3(a)). 从图3(a)可看出,-直接带隙约为5.9eV. 再运用GW近似, 求解准粒子有效哈密顿量本征方程, 计算得到GW近似准粒子能带结构(图3(b)),-直接带隙约为9.9eV. GW修正使带隙增大了约4eV.

图3 LiCl(001)-(1X1)干净表面的能带
3 CO:LiCl(001)-(1X1)表面的电子激子态
对于CO分子在LiCl(001)-(1X1)表面上的吸附特性, 本文不考虑温度的影响, 只考虑接近绝对零度时的吸附结构. 所采用的周期性超晶胞包含1个CO分子层、6层衬底原子(6个LiCl原子层), 以及1.2nm厚的真空层. 首先, 考虑CO分子竖直放置, 且O原子在C原子上方, 而C原子吸附在衬底Cl原子正上方、Li原子正上方以及Li原子和Cl原子之间空位的上方; 然后考虑CO分子倒过来(C原子竖直位于O原子上方), 而O原子吸附于上述衬底的3个位置上; 最后考虑CO分子的倾斜吸附. 对于上述每种吸附, 利用局域密度近似的密度泛函理论计算原子受力, 优化衬底原子的竖直位置以及CO分子的键长, 使所有原子的受力小到可以忽略为止, 并计算系统的总能量. 比较不同种吸附时系统的总能量发现, CO分子垂直吸附, 且C原子吸附在Li原子的正上方时, 系统的总能量最低. 此时C―O键长为0.113nm, C―Li键长为0.213nm. 吸附结构如图4所示.
运用GW近似, 计算CO:LiCl(001)-(1X1)表面的准粒子能带结构, 结果如图5(b)所示. 图5(b)中竖线表示LiCl块体能带对(001)面的投影. 将CO: LiCl(001)-(1X1)表面的超晶胞中所有衬底原子层移去, 得到对应的孤立CO分子层的周期性超晶胞. 为了弄清孤立CO分子层的能带, 利用孤立CO分子层的周期性超晶胞, 计算孤立CO分子层的GW近似的准粒子能带结构, 计算结果如图5(a)所示. 由于分子层在表面内的周期性, 以及邻近CO分子之间的距离只有0.356nm, 故孤立CO分子层的GW能带呈现出明显的色散关系.
在图5(a)中, CO分子的价带4σ位于-9.7eV, 价带1π位于-6.9~-6.1eV之间, 价带5σ能量在-4.2~-3.4eV之间, 未占据带2π*能量在11~12.9 eV范围. CO分子的HOMO-LUMO能隙约是14eV. 对比图5(a)与图5(b), CO分子的价带和最低的未占据带与衬底LiCl的能带基本分开; 在吸附后, CO分子的价带移动较小, 但CO分子的未占据带2π*移动较大, 约下移1.6eV.
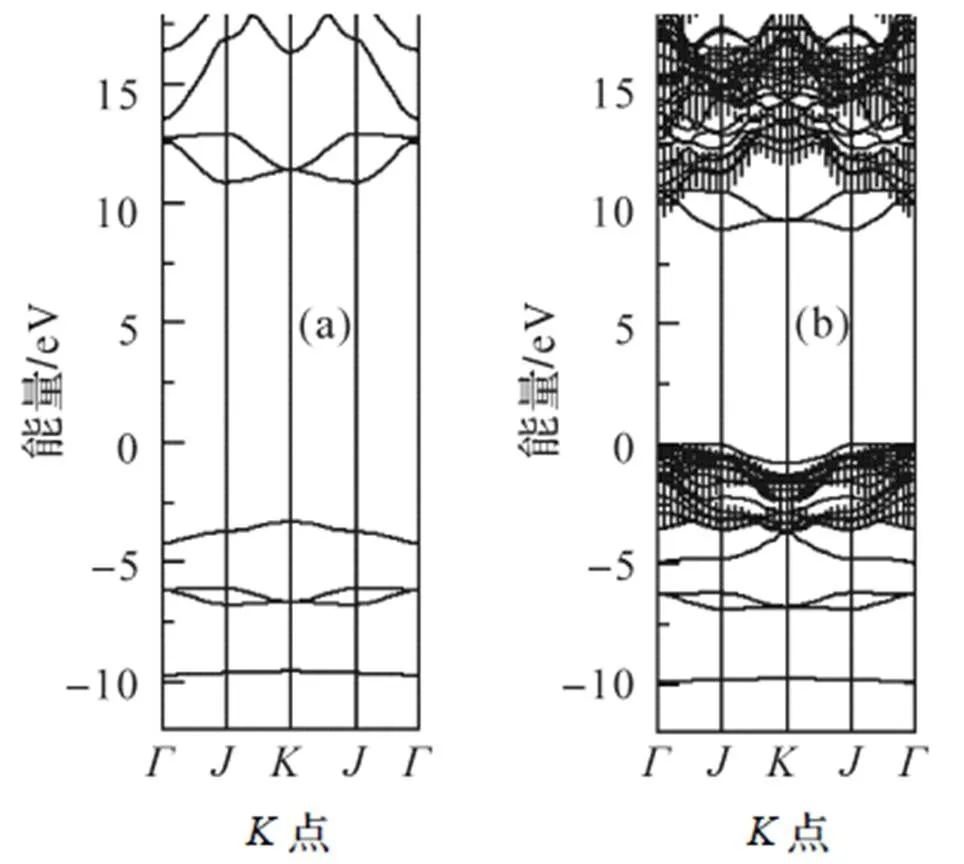
图5 孤立CO分子层和CO:LiCl(001)-(1X1)表面的能带


图6 孤立CO分子层光吸收谱(a)与CO:LiCl(001)-(1X1)表面的光吸收谱(b)
对于CO:LiCl(001)-(1X1)表面的BS方程, 考虑最高的28个价带(其中有24个价带属于衬底带, 另有4个价带是CO分子带)和最低的27个导带(包含24个衬底导带和3个CO分子导带). 求解BS方程, 并得出光致激发态的激发能和波函数, 即可计算CO:LiCl(001)-(1X1)表面的光吸收谱, 其结果如图6(b)所示. 当激发能为7.3eV时, 出现第1个吸收峰,此最低激子态主要描述衬底Cl原子的3p态到CO分子2π*态的跃迁, 即由衬底到CO分子的电荷转移.
4 在CO:LiCl(001)-(1X1)表面上分子激子态的随时演化

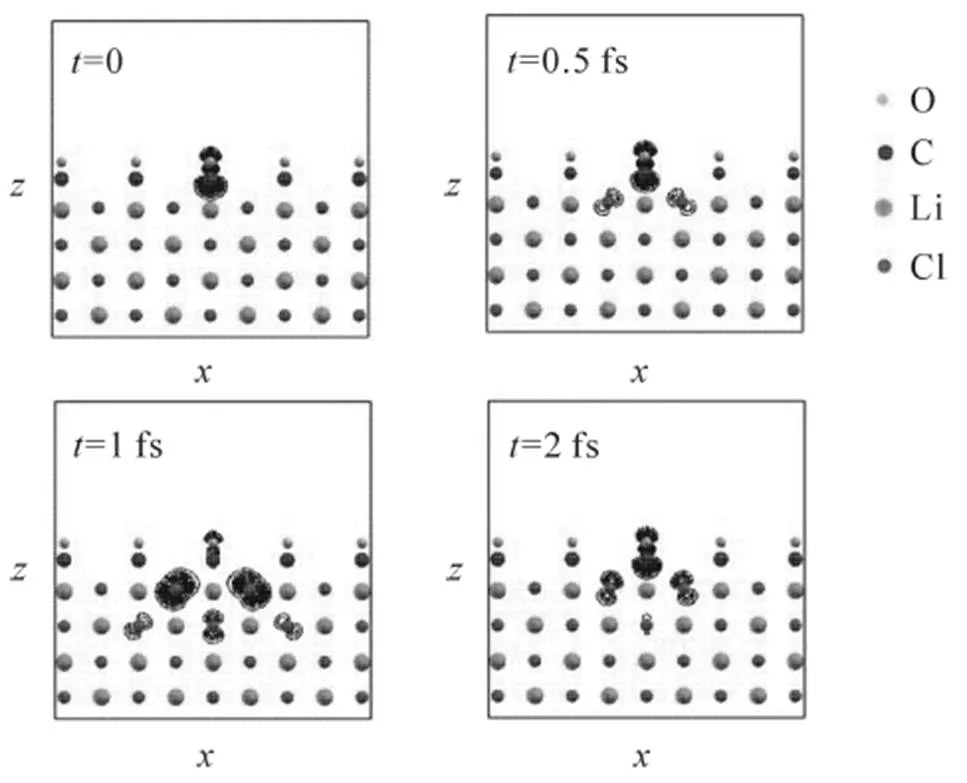
图7 孤立CO分子激子态空穴密度分布的随时演化
从图7不难看出, 当=0时, CO分子激子态的空位几乎全部存在CO分子上, 该密度分布即为CO的5σ态的密度分布. 然而, 随着时间的推进, 分子激子态的空位开始跃迁到衬底层Cl原子的3p轨道上. 当=0.5fs时, 已有相当幅度的空穴移到衬底, 在=1fs时, 绝大部分空穴已移到衬底, 在=2fs时, 空穴触及衬底下表面后发生反射. 类似地, 将空穴的坐标固定在CO分子的C原子上, 可计算分子激子态的电子分布的随时演化, 但发现分子激子态的电子始终分布在CO分子上, 不向衬底移动.
为了更清楚地看出分子激子态的电子和空穴沿垂直于表面方向的传播, 定义电子和空穴坐标的关联函数为:

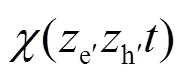
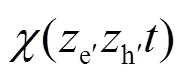

图8 电子-空穴波函数的ze-zh关联性
CO分子激子态的存活率是定量描述该激子态衰变过程的量, 其定义为:
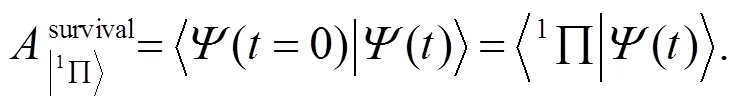
利用式(12)和(14), 计算瞬时产生的CO分子激子态在LiCl(001)-(1X1)表面随时演化过程中每一时刻的存活率, 结果如图9所示. 图9中实线表示CO分子激子态存活率的随时变化, 虚线表示exp(-t/0.75). 从图9可发现, 在初始时间(t≤1fs), 分子激子态几乎按指数规律衰变, 而且衰变很快, 寿命τ=0.75fs. 当t=1fs时, 存活率衰减到大约20%. 1fs以后, 分子激子态的存活率表现出小幅振荡. 结合图8可知, CO分子激子态的空穴由CO分子往衬底传播, 触及衬底的下表面会往回传播.

5 结语
本文利用多体摄动理论的GW近似计算了LiCl块体的准粒子能带结构, 得到的带隙与实验吻合; 再运用二粒子格林函数理论引入电子-空穴相互作用, 并求解BS方程, 计算LiCl块体的光吸收谱, 其数值结果很好地再现了实验所观测的吸收峰对应的激发能和强度.
利用局域密度近似的密度泛函理论计算了CO分子吸附于LiCl(001)-(1X1)表面的几何结构. 在此基础上运用GW近似, 计算了CO:LiCl(001)-(1X1)表面的准粒子能带结构, 并在二粒子格林函数理论框架下考虑电子-空穴相互作用, 求解BS方程, 计算CO:LiCl(001)-(1X1)表面的电子-空穴激发态和光吸收谱.
[1] Pietzsch A, Föhlisch A, Beye M, et al. Towards time resolved core level photoelectron spectroscopy with femtosecond X-ray free-electron lasers[EB/OL]. [2019- 03-04]. https://iopscience.iop.org/article/10.1088/1367-2630/10/3/033004/pdf.
[2] Chulkov E V, Borisov A G, Gauyacq J P, et al. Electronic excitations in metals and at metal surfaces[J]. Chemical Reviews, 2006, 106(10):4160-4206.
[3] Shibuta M, Hirata N, Matsui R, et al. Charge separation at the molecular monolayer surface: Observation and control of the dynamics[J]. The Journal of Physical Chemistry Letters, 2012, 3(8):981-985.
[4] Reinert F, Huefner S. Photoemission spectroscopy—from early days to recent applications[EB/OL]. [2019-03-04]. https://iopscience.iop.org/article/10.1088/1367-2630/7/1/097/pdf.
[5] Kirkegaard C, Kim T K, Hofmann Ph. Self-energy determination and electron-phonon coupling on Bi(110) [EB/OL]. [2019-03-04]. https://iopscience.iop.org/article/ 10.1088/1367-2630/7/1/099/pdf.
[6] Matzdorf R. Investigation of line shapes and line intensities by high-resolution UV-photoemission spectro- scopy—Some case studies on noble-metal surfaces[J]. Surface Science Reports, 1998, 30(4/5):153-206.
[7] Dose V. Momentum-resolved inverse photoemission[J]. Surface Science Reports, 1985, 5(8):337-378.
[8] Smith N V. Inverse photoemission[EB/OL]. [2019-03- 04]. https://iopscience.iop.org/article/10.1088/0034-4885/ 51/9/003/pdf.
[9] Giesen K, Hage F, Himpsel F J, et al. Two-photon photoemission via image-potential states[J]. Physical Review Letters, 1985, 55(3):300-303.
[10] Schoenlein R W, Fujimoto J G, Eesley G L, et al. Femtosecond studies of image-potential dynamics in metals[J]. Physical Review Letters, 1988, 61:2596-2599.
[11] Güdde J, Höfer U. Femtosecond time-resolved studies of image-potential states at surfaces and interfaces of rare- gas adlayers[J]. Progress in Surface Science, 2005, 80: 49-91.
[12] Hedin L. New method for calculating the one-particle Green’s function with application to the electron-gas problem[J]. Physical Review, 1965, 139:A796-A823.
[13] Hedin L, Lundqvist S. Effects of Electron-Electron and Electron-Phonon Interactions on the One-Electron States of Solids[M]. New York: Academic Press Incorporated, 1969:1.
[14] Sarria I, Osma J, Chulkov E V, et al. Self-energy of image states on copper surfaces[J]. Physical Review B, 1999, 60:11795-11803.
[15] Yi Z, Ma Y, Rohlfing M, et al. Quasiparticle band structures and lifetimes in noble metals using Gaussian orbital basis sets[EB/OL]. [2019-03-04]. https://journals. aps.org/prb/pdf/10.1103/PhysRevB.81.125125.
[16] Springer M, Aryasetiawan F, Karlsson K. First-principles T-matrix theory with application to the 6eV satellite in Ni[J]. Physical Review Letters, 1998, 80:2389-2392.
[17] Zhukov V P, Chulkov E V, Echenique P M. GW+T theory of excited electron lifetimes in metals[EB/OL]. [2019- 03-04]. https://journals.aps.org/prb/pdf/10.1103/PhysRevB.72.155109.
[18] Shumay I L, Höfer U, Reuß Ch, et al. Lifetimes of image-potential states on Cu(100) and Ag(100) measured by femtosecond time-resolved two-photon photoemission [J]. Physical Review B,1998, 58:13974-13981.
[19] Borisov A G, Gauyacq J P, Kazansky A K. Scattering by alkali adsorbates as a decay mechanism for image potential states on Cu surfaces[J]. Surface Science, 2002, 505:260-270.
[20] Kevan S D. Direct measure of surface impurity scattering by angle-resolved photoemission[J]. Physical Review B, 1986, 33:4364-4366.
[21] Wang X Y, Paiella R, Osgood R M Jr. Two-dimensional electron-scattering processes on Na-dosed Cu(111): A two-photon photoemission study[J]. Physical Review B, 1995, 51:17035-17039.
[22] Wallauer W, Fischer R, Fauster Th. Influence of adsorbates on the image states of Pd(111)[J]. Surface Science, 1996, 364:297-302.
[23] Boger K, Weinelt M, Fauster Th. Scattering of hot electrons by adatoms at metal surfaces[EB/OL]. [2019- 03-04]. https://journals.aps.org/prl/pdf/10.1103/PhysRev Lett.92.126803.
[24] Fauster Th, Weinelt M. Carrier dynamics on surfaces studied by two-photon photoemission[J]. Surface Science, 2005, 593:1-11.
[25] Borisov A G, Gauyacq J P, Kazansky A K, et al. Long-lived excited states at surfaces: Cs/Cu(111) and Cs/Cu(100) systems[J]. Physical Review Letters, 2001, 86:488-491.
[26] Borisov A G, Gauyacq J P, Chulkov E V, et al. Lifetime of excited electronic states at surfaces: Comparison between the alkali/Cu(111) systems[EB/OL]. [2019-03-04]. https:// journals.aps.org/prb/pdf/10.1103/PhysRevB.65.235434.
[27] Gauyacq J P, Borisov A G. Excited electron transfer between a core-excited Ar*(2p3/2-14s) atom and the metal substrate in the Ar/Cu(111) system[EB/OL]. [2019-03-04]. https://journals.aps.org/prb/pdf/10.1103/PhysRevB.69.235408.
[28] Vijayalakshmi S, Foehlisch A, Hennies F, et al. Surface projected electronic band structure and adsorbate charge transfer dynamics: Ar adsorbed on Cu(111) and Cu(100) [J]. Chemical Physics Letters, 2006, 427:91-95.
[29] 孔维孟, 杨宗献, 张喜林, 等. 单原子Pt增强α- Mo2C(0001)抗硫中毒特性机理的第一性原理研究[J]. 原子与分子物理学报, 2018, 35:383-388.
[30] 梁冬梅, 冷霞, 马玉臣. 多体格林函数方法对g-CN激发态特性的研究[J]. 中国科学: 化学, 2016, 46(1):126- 132.
[31] Onida G, Reining L, Rubio A. Electronic excitations: Density-functional versus many-body Green’s-function approaches[J]. Reviews of Modern Physics, 2002, 74: 601-659.
[32] 周晓林, 宗江琴, 王海燕, 等. Ne-CH4分子间相互作用势的局域密度近似计算[J]. 原子与分子物理学报, 2004, 21:525-528.
[33] Hahn P H, Schmidt W G, Bechstedt F. Bulk excitonic effects in surface optical spectra[EB/OL]. [2019-03-04]. https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.88.016402.
[34] Wang N P, Rohlfing M, Krüger P, et al. Quasiparticle band structure and optical spectrum of LiF(001)[EB/OL]. [2019-03-04]. https://journals.aps.org/prb/pdf/10.1103/PhysRevB.67.115111.
[35] 黄美纯. 激发态过程的多体理论方法[J]. 发光学报, 2005, 26(3):273-284.
[36] 潮晴, 王能平. 锂的卤化物LiX(X=F,Cl,Br,I)的镜像势态[J]. 宁波大学学报(理工版), 2019, 32(4):73-80.
[37] Strinati G. Dynamical shift and broadening of core excitons in semiconductors[J]. Physical Review Letters, 1982, 49:1519-1522.
[38] Strinati G. Effects of dynamical screening on resonances at inner-shell thresholds in semiconductors[J]. Physical Review B, 1984, 29:5718-5726.
[39] 潘播, 王能平. 基于多体摄动理论的CaO电子能带结构及光吸收谱的研究[J]. 宁波大学学报(理工版), 2017, 30(1):94-98.
[40] Wright S, Hasselbrink E. Photodesorption of disilane- physisorbed on hydrogen terminated Si(100) and the dramatic consequences of weak molecular chemisorption [EB/OL]. [2019-03-04]. https://aip.scitation.org/doi/pdf/ 10.1063/1.1359521.
[41] Hohenberg P, Kohn W. Inhomogeous electron gas[J]. Physical Review, 1964, 136:864-871.
[42] Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects[J]. Physical Review, 1965, 140:1133-1138.
[43] Ceperley D M, Alder B J. Ground state of the electron gas by a stochastic method[J]. Physical Review Letters, 1980, 45:566-569.
[44] Hamann D R. Generalized norm-conserving pseudo- potentials[J]. Physical Review B, 1989, 40:2980-2987.
[45] Rohlfing M, Krüger P, Pollmann J. Efficient scheme for GW quasiparticle band-structure calculations with applications[J]. Physical Review B, 1995, 52:1905-1917.
[46] Rohlfing M, Louie S G. Electron-hole excitations and optical spectra from first principles[J]. Physical Review B, 2000, 62:4927-4944.
[47] Kunz A B. Study of the electronic structure of twelve alkali halide crystals[J]. Physical Review B, 1982, 26: 2056-2069.
[48] Eby J E, Teegarden K J, Dutton D B. Ultraviolet absorption of alkali halides[J]. Physical Review, 1959, 116:1099-1105.
[49] Ching W Y, Gan F, Huang M Z. Band theory of linear and nonlinear susceptibilities of some binary ionic insulators [J]. Physical Review B, 1995, 52:1596-1611.
The excited electronic state and its time evolution of CO adsorbed on LiCl(001)-(1X1)
CHEN Wuchao, WANG Nengping*
( School of Physical Science and Technology, Ningbo University, Ningbo 315211, China )
The many-body perturbation theory is used to study the properties of excited electronic states of the CO molecule adsorbed on LiCl(001)-(1X1) surface, and further investigate the time evolution of the CO exciton state as well as the lifetime of the exciton state. At first, density-functional theory within local density approximation is used to calculate the ground state geometry of CO adsorbed on LiCl(001)-(1X1) surface. Next, the quasiparticle band structures of bulk LiCl, of the LiCl(001)-(1X1) surface, and of CO adsorbed on the surface are evaluated within the GW approximation. Moreover, by taking the electron-hole interaction into consideration, the electron-hole excitation states and their optical spectra are obtained from the solution of the Bethe-Salpeter equation within the theory of the two-particle Green function. The obtained optical spectra are compared with available experimental results. Finally, based on the solution of the BSE for the adsorbate system CO:LiCl(001)-(1X1), the time evolution of the CO exciton state is studied using the time-dependent Schrödinger equation. At the initial stage, the CO exciton state exhibits a very fast decay due to the coupling of the adsorbate with the substrate, and the lifetime of the CO exciton state is only 0.75 fs. The electron of the molecule exciton state remains on the molecule while its hole is mostly transferred into the LiCl substrate.
quasiparticle band structure; GW approximation; excited electronic states; BSE; time evolution
O485
A
1001-5132(2020)01-0101-09
2019−07−29.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
国家自然科学基金(11074136).
陈武超(1990-), 女, 山东临沂人, 在读硕士研究生, 主要研究方向: 低维材料激发态. E-mail: 2283832766@qq.com
王能平(1961-), 男, 江西九江人, 研究员, 主要研究方向: 凝聚态理论及计算物理. E-mail: wangnengping@nbu.edu.cn
(责任编辑 史小丽)

