高堑边坡锚索加固设计参数的优化——以厦门北站环山路为工程案例

郑朝晖

(厦门中平公路勘察设计院有限公司 福建厦门 361000)

0 引言

道路交通是经济发展的命脉，通达快捷的路网是促进地区经济进一步发展的先决条件。跟随着城镇化脚步的前进，越来越多的地区建设大量的高速公路、国省干线。这些地区不乏恶劣的地质条件，道路沿线，高路堤、深路堑频繁出现，高边坡稳定分析的重要性日渐凸显。

框架锚索防护作为典型轻型防护形式在高堑坡防护中应用频繁，压力分散型锚索因为其具有锚固段端部峰值应力小，能够提供更大的锚固力等优势成为了锚索中的主流[1]。通过边坡安全系数反算锚固力、锚固长度，再对不同锚索单元进行力值分配是现在大部分工程采用的设计方法，但是压力分散性长锚索加固受力特性复杂，力学分析困难，尤其是这种设计方法忽略了工后变形对锚索锚固力的影响，难以对其进行力学分析，因此要采用数值分析方法，预估不同工况产生的变形，进而对锚索加固设计参数进行优化。

基于此，本文拟以厦门北站环山路为工程案例，探讨高堑边坡锚索加固设计参数的优化，与同仁交流。

1 工程概况

厦门集美新城岩内片区环山路工程位于厦门北站北广场，是北广场路网的重要组成部分，是岩内车辆基地上盖保障性住房居民出行的重要通道。路线沿石堀山山体展线，全长5.159km，起点段1.4km为城市次干道，其余路段为城市支路。道路沿线经过地区多为低山丘陵与残丘台地相间，局部地段沟谷发育，地形总体稍有起伏，地势为西北高、东南低，呈阶梯状下降，高程约为22.97m～90.40m，沿线多处边坡高达30m～40m，边坡防护设计成为该工程设计的重点、难点。

环山路K3+700处与厦安高速岩凤溪隧道K9+568.594(运营桩号)交叉，交叉角度54°50′57″，道路路线K3+620～K3+740段，布设于凤溪隧道上方，采用路基方案上跨，长度约120m，边坡高度约18m～27m，三级边坡。根据工程地质钻孔揭露及结合现场地质测绘调查，开挖边坡处，表层覆盖层为粉质粘土，残积砂质粘性土，覆盖层下主要为燕山晚期中粗粒花岗岩，按其风化程度分为全、强、中、微风化4个亚层，钻探揭露的深度范围内中风化基岩节理裂隙很发育～发育，岩芯破碎～较完整，由上而下,依次为：全风化花岗岩、砂土状强风化花岗岩、碎块状强风化花岗岩、中风化花岗岩。

具体工程设计方案如图1所示：

(1)内侧边坡第一、第二级坡率为1∶1，采用预应力锚索框架进行防护，锚索采用压力分散型，竖向间距4m，水平间距3m，单孔4根直径为15.2×10-3m钢绞线，锚固长度10m，预应力值初定采用300kN，其中单元一长度20m，单元二长度为15m。

(2)内侧边坡第三级为1∶1.25，采用一般植草坡面防护，下同。

(3)道路外侧采用悬臂式轻型挡墙，挡墙高度为4.5m，埋置深度大于1m。

图1 高边坡地质横断面示意图

2 锚索设计、张拉

根据《建筑边坡工程技术规范》(GB 50330-2013)规范要求，一级边坡锚杆杆体抗拉安全系数为2.2，岩土锚固体抗拔安全系数为2.6。

钢绞线极限抗拉强度1860MPa，因此锚索单元极限张拉荷载：

Npk1=1860×0.00014×2=520.8kN>150×2.2=330kN，满足要求。

锚固段位于碎块状强风化花岗岩，根据地勘资料，地层与锚固体粘结强度极限值采用320kPa，因此锚固体极限粘结力为：

Npk2=3.14×0.13×5×320×5=653.1kN>150×2.6=390kN，满足要求。

压力分散型锚索应先对较长的锚索单元进行先补偿张拉，之后单元一、单元二再一同张拉，进而使得锚索不同单元最终锁定的力值相等[2]。锚索张拉分析如下：

S1=N1L1/2EA=150×20/(2×19 500×0.00 014)=0.055m

S2=N2L2/2EA=150×15/(2×19 500×0.00 014)=0.041m

△S=S1-S2=0.055-0.041=0.014m

△N1=2EA△S/L1=2×19 500×0.00 014×0.014/20=37.5kN

其中：N1、N2分别为单元一、单元二拉力，为150kN；

L1、L2分别为单元一、单元二长度，L1=20m，L2=15m；

E为钢绞线弹性模量；

A为单根锚索长度；

△S为单元一、单元二差异伸长量；

△N1为单元一补偿张拉力；

锚索单元分布张拉如表1所示。

表1 锚索单元分步张拉 kN

这种应力张拉方式先对单元一进行补偿张拉，之后第一、第二单元共同张拉，使得单元一、单元二受力大致相等。这种张拉方式基于边坡工后不产生变形的假定，但是实际工程中，为了保证边坡的安全稳定，均要求施工单位边坡开挖后应立即进行坡面防护，同时要求在上一级边坡防护实施完成后，才能对下一级边坡进行开挖。因此，多级边坡开挖过程中，应充分考虑下级边坡开挖对上级边坡变形的影响，避免边坡变形过大，导致锚索拉力超过极限值，同时应考虑变形对补偿拉力的影响，对边坡变形进行预估，避免同一锚索不同单元受力差别过大，受力不均，影响锚索的整体受力性能。采用数值分析方法，可以对不同工况下的变形进行分析，对锚索参数进行优化设计。

3 应用数值分析方法优化锚索加固设计参数

3.1 Abaqus有限元模型的建立

模型运用岩土界内知名有限元Abaqus构建，其中土体采用三节点线性平面三角形单元，采用摩尔-库伦模型塑性本构模型[3]；框架采用四节点双线性平面应变四边形单元，采用弹性模型，考虑框架作用主要是将锚索作用力传递给土体，因此通过放大竖肋截面，简化横梁的方式进行框架等效；锚索采用二节点二维桁单元，采用弹性模型；锚索预应力采用降温法，即在模块中定义温度膨胀系数，然后在分析步中降低温度，以达到施加预应力的效果。有限元模型网格划人如图2所示，计算公式如下：

△T=N/aEA

其中：△T为降低温度值，N为施加的预应力值，E为锚索弹性模量，A为截面面积，a为膨胀系数。

模型分析过程中建立多个分析步以模拟不同施工工况，具体工况及施工内容如表2所示。

图2 有限元模型网格划分

表2 工况及实施内容

3.2 设计参数

根据勘察资料，计算参数见表3。

表3 计算采用物理力学参数

3.3 数值模拟结果及分析

将边坡、框架、锚索单元进行装配组合，锚索与框架进行绑定处理，模拟边坡开挖和施加锚索的工序。开挖后土体变形如图3所示，最大位移位于第一边坡处，约15.5cm。

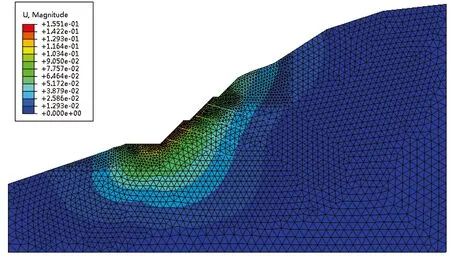
图3 边坡变形云图

图4 二级边坡第一道锚索变形(S21=0.023m)—工况6

第六阶段对第一级边坡进行开挖，开挖过程使第二级已施加预应力的锚索产生变形，如图4～图5所示，第一级边坡开挖引起第二级边坡第一道锚索变形△S21=0.023m，引起第二级边坡第二道锚索变形 △S22=0.031m。

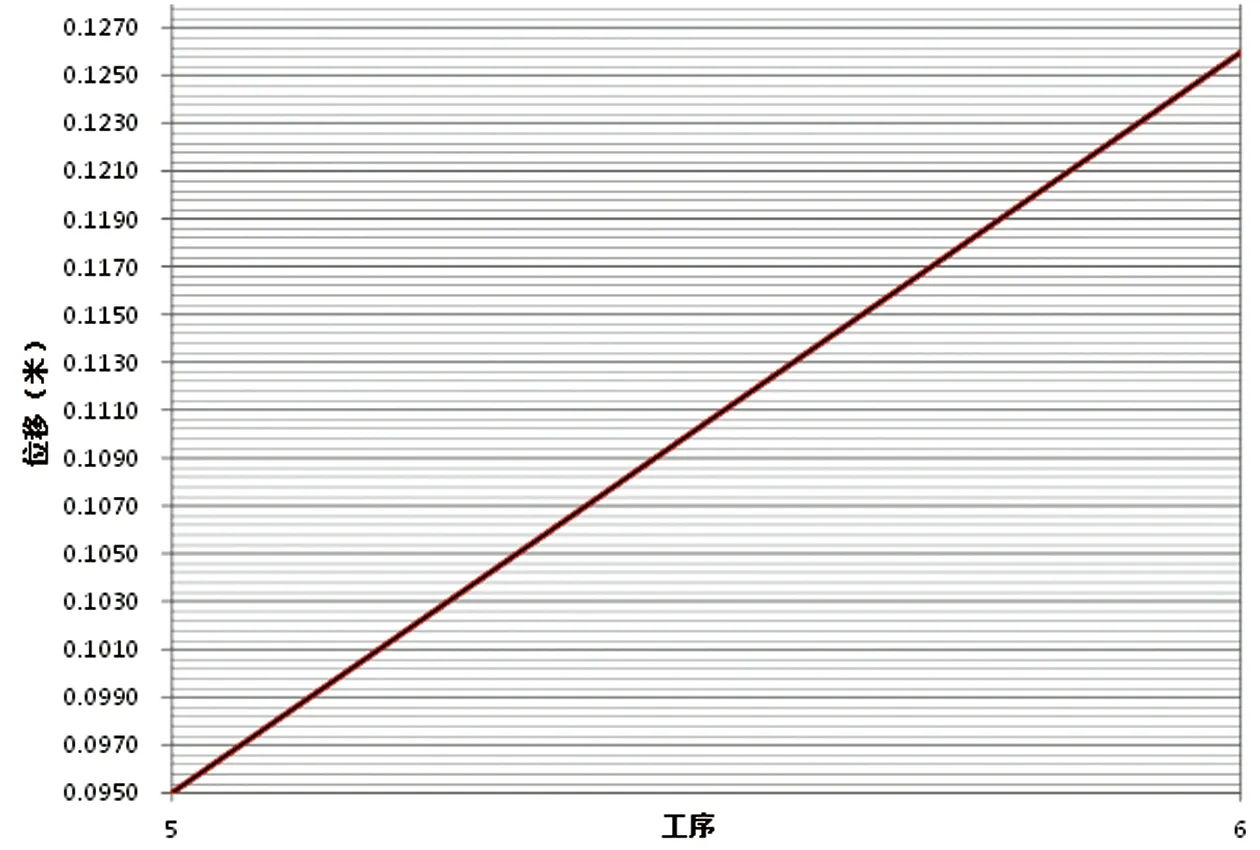
图5 二级边坡第二道锚索变形(S22=0.031m)—工况6

考虑边坡变形引起的附加拉力，第二级边坡锚索拉力，如表4所示。

表4 第二级边坡锚索拉力 kN

3.4 锚索拉力优化调整

根据《建筑边坡工程技术规范》(GB50330-2013)第8.2.2条规定，锚杆杆体抗拉安全系数应大于2.2，因此考虑满足规范要求，同时使框架受力更为均衡协调，同一片框架不同锚索不同单元差异荷载均控制在15%范围，因此该次设计第二级边坡第一道锚索预应力为150kN，第二道锚索预应力调整为125kN。调整后锚索拉力如表5所示。

表5 锚索单元分步张拉 kN

运用理正岩土软件进行稳定计算，同时运用Abaqus有限元软件强度折减法进行复核验算，最终确定边坡稳定系数可达1.67。

4 结论

不同工况的变形所产生的附加荷载对锚索的影响较大，尤其是在土质情况较差，变形较大的边坡，这种附加荷载是不可忽视的。

采用数值分析方法，预测不同工况引起的变形，对工程设计的参数合理性的论证，对不同锚索的不同单元进行具体设计、优化是必要的。

施工过程在坡体布置变形控制点，对设计方案进行复核，对施工过程进行预警，实施动态设计，有利于确保工程安全。