基于行车激励的桥梁动力性能测试与状态评估

关孝文，张 莉，胡世浩，张效军

(1.公路建设与养护技术、材料及装备交通运输行业研发中心(甘肃路桥建设集团有限公司)，甘肃 兰州 730030；.甘肃智通科技工程检测咨询有限公司， 甘肃 兰州 730050；3.天祝县自然资源局， 甘肃 武威 733299； 4.兰州交通大学， 甘肃 兰州 730070)

桥梁结构的动力特性是桥梁承载能力评定的重要参数，同时也是识别桥梁结构工作性能的重要参数[1-3]。任何结构都可看作是由刚度、质量、阻尼矩阵构成的动力学系统，结构一旦出现损伤，其动力学参数也随之变化，这种变化可视为结构损伤发生的标志。因此，基于动力特性的损伤识别和状态评估越来越受到人们的关注[4-6]，而测试动力特性的准确性是桥梁损伤识别和状态评估可靠性的关键因素。

在桥梁动力特性测试的过程中，为了能够获得更高信噪比的响应信号，往往采用行车的方式给桥梁进行激振，例如跳车试验、匀速跑车试验等[7-9]。根据研究资料显示，采用行车激励的方式对桥梁进行激振的过程会伴随着车桥耦合振动的发生[10-13]，而这一振动信号的产生将对我们测试桥梁实际自振特性产生影响，而且在结构自重较轻，激励车辆荷载较重的情况下这一影响还会继续放大。从目前的研究情况来看大都通过概率统计获得频率加权平均值的方法排除这种耦合振动带来的干扰[14-15]，但我们从行车激励的动态历程来看，车桥耦合振动发生在车辆上桥后和下桥前的这段时间内，这段时间桥梁处于受迫振动状态，而当车辆驶出桥梁时，结构处于一种自由衰减的振动状态，选取此时的频域曲线进行分析可有效避免车辆对桥梁自振频率的影响。

基于以上论述，作者以一座简支钢混叠合梁桥为例，采用行车激励的方式对该桥的动力性能进行了测试.本文通过动应变时程曲线判断车辆出桥时间，以此时间为节点，选择车辆出桥后的频域曲线进行分析，以验证采用行车激励法测试桥梁动力性能的有效性和准确性。

1 桥梁概况

该桥为国道312线嘉峪关至清泉段公路(试验段)上跨高速公路而建的钢混叠合梁桥，桥梁全长53 m，计算跨径45 m，路基宽度12 m，行车道宽度采用3.75 m，设计时速为80 km/h，结构形式为单跨简支梁。桥梁钢结构部分采用全焊接钢梁，钢梁由端横梁、主梁(三片槽型钢梁)、横隔梁及加劲肋组成，钢梁上翼板顶面设置钢钉与混凝土桥面板连为整体,各构件截面尺寸如图1所示，主梁钢材采用Q345D钢板；桥面板采用微膨胀C50混凝土分块预制，板间采用现浇湿接缝连接方式；剪力钉采用Φ22 mm圆头焊钉，高度170 mm，根据不同的受力需要，剪力钉在沿桥纵向采用150 mm～300 mm的间距进行设置，全桥测试断面布设如图2所示。钢混叠合梁的内部细构如图3所示。

图1 桥梁典型横断面图

图2 全桥测试断面布设图

图3 钢混叠合梁内部结构

2 结构有限元分析

本项目采用MIDAS/Civil软件建模进行模拟计算。采用梁格法建模，叠合梁、横隔梁以及虚拟横梁均采用梁单元模拟；钢主梁与混凝土桥面板组合截面等效为钢截面模拟，本文采用混凝土单轴受压应力-应变关系模型，以及简化后钢材的应力-应变本构关系，以保证混凝土与等效后钢梁变形相等，即变形前后构件的抗弯刚度相等为原则，进行截面等效，等效后钢截面可视为均质各项同性弹性体；二期恒载根据桥梁设计铺装进行添加。添加边界条件时固定端约束Dx，Dy，Dz，Rx，Rz，使之只能绕y轴转动，可变端约束Dy，Dz，Rx，Rz，使之能绕y轴转动和x方向移动。根据模型计算，该钢混叠合梁桥一阶竖向弯曲基频为2.387 Hz，计算模型如图4右侧图例所示。

图4 第一阶竖弯

为了验证所建模型的正确性，本文采用初等梁理论计算的挠度和所建模型求解的挠度进行比较，具体过程如下：

初等梁理论的简化计算图如图5所示。

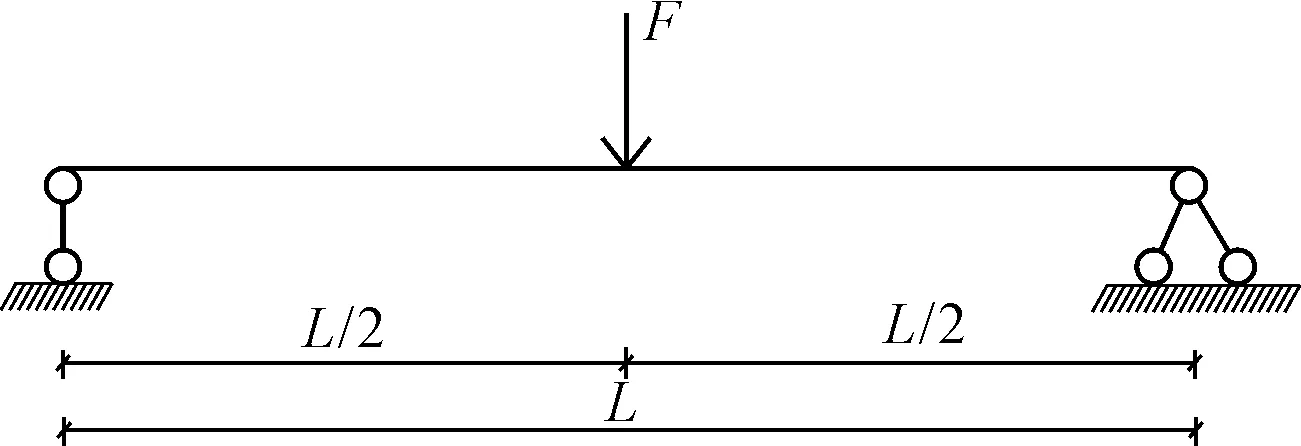
图5 初等梁理论加载图

跨中挠度采用式(1)计算：

(1)

式中：f为简支梁的挠度；F为跨中集中荷载，本文中取F=500 kN；E为换算截面的弹性模量；I为换算截面的惯性矩；L为简支梁的跨径。截面换算过程中将有效宽度内混凝土桥面板的截面积等效成钢梁上翼缘的截面面积的一部分，从而把研究对象等效为更利于分析的单一材料的钢梁截面。此时E即为Q345D钢板的弹性模量2.06×1011N/m2，I亦等于组合截面的惯性矩，通过MIDAS截面特性计算得I=0.735 m4。比较结果如表1所示。

MIDAS/Civil有限元挠度计算值如图6右侧的图例所示。

表1 跨中挠度对比表 单位：mm

图6 MIDAS/Civil有限元挠度计算值

通过对表1的数据分析，我们可以看出，挠度的MIDAS/Civil有限元计算值与初等梁理论计算值的误差为3.0%，误差在5%以内，验证了所建立有限元模型的正确性。

3 现场试验与分析

3.1 试验详情

根据结构理论分析结果，在全桥布设3个控制断面，测试行车激励后结构基频、阻尼比及动荷载作用下的冲击系数。拾振器桥面布设如图7所示，跨中动应变测点布置如图8所示。

动载试验采用一辆满载40 t三轴重型货车进行跑车试验，分别以20 km/h、30 km/h、40 km/h、50 km/h的速度匀速通过测试桥跨，同时采集各测点的响应信号。

图7 拾振器桥面布设图

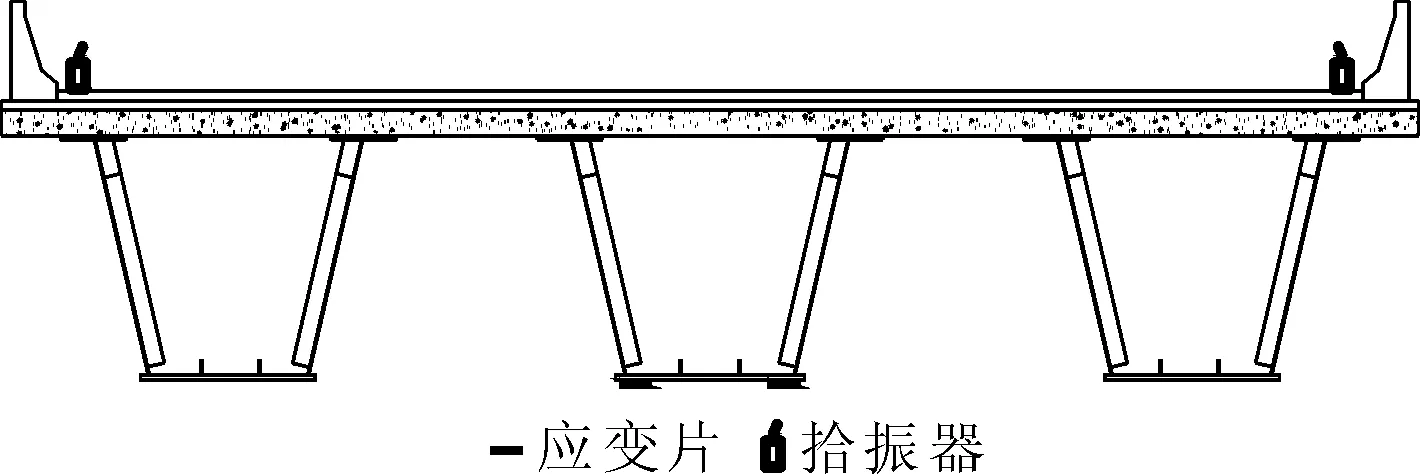
图8 跨中动应变测点布置图

3.2 结构自振特性分析

根据《公路桥梁荷载试验规程》[16](JTG/T J21-01—2015)中关于简支梁桥自振特性测试阶次的要求，本次试验测试了该桥的一阶自振频率。本试验采用了北京东方振动与噪声技术研究所生产的INV1861A动态信号采集分析系统.以跨中3#测点的振动信号为例，采用全程波形分析和车辆出桥后自由振动波形分析对结构基频进行分析，车辆出桥的时间节点通过动应变时程曲线进行辅助判断。

采用不同的数据后处理方式得出的测试频率与理论值对比如表2所示。

通过测试数据的分析可以看出，行车激励能够有效的对被测桥梁起到激振作用，从而获取更高信噪比的响应信号；在数据后处理时准确选取自由振动曲线进行频谱分析是能否准确分析结构基频的关键，这种分析方法能够有效规避全程分析中车辆对结构自振特性的影响；激励车速只用于保证车辆对结构的激振效果，不影响测试结果；桥梁实测自振频率大于理论计算频率，桥梁整体刚度较好.仅以该桥的测试结果来看，车辆低速通过桥梁时已经能够对桥梁起到有效的激振，且此时车辆的自振频率与该桥梁自振频率接近，他们之间发生振动耦合，车辆对桥梁自振特性的影响达到了最大化，而此时选用全程波形进行频谱分析，其分析结果显然是失真的，如表2所示；而当车辆以较高车速通过桥梁时，其自振频率明显大于桥梁自振频率，对桥梁自振特性影响较小，此时选用全程波形分析亦能准确分析该桥的基频。

表2 不同数据后处理方式下频率实测值与理论值的对比

3.3 结构振型分析

结构振型通过布设在桥面两侧的拾振器频响幅值进行拟合，如图9所示。

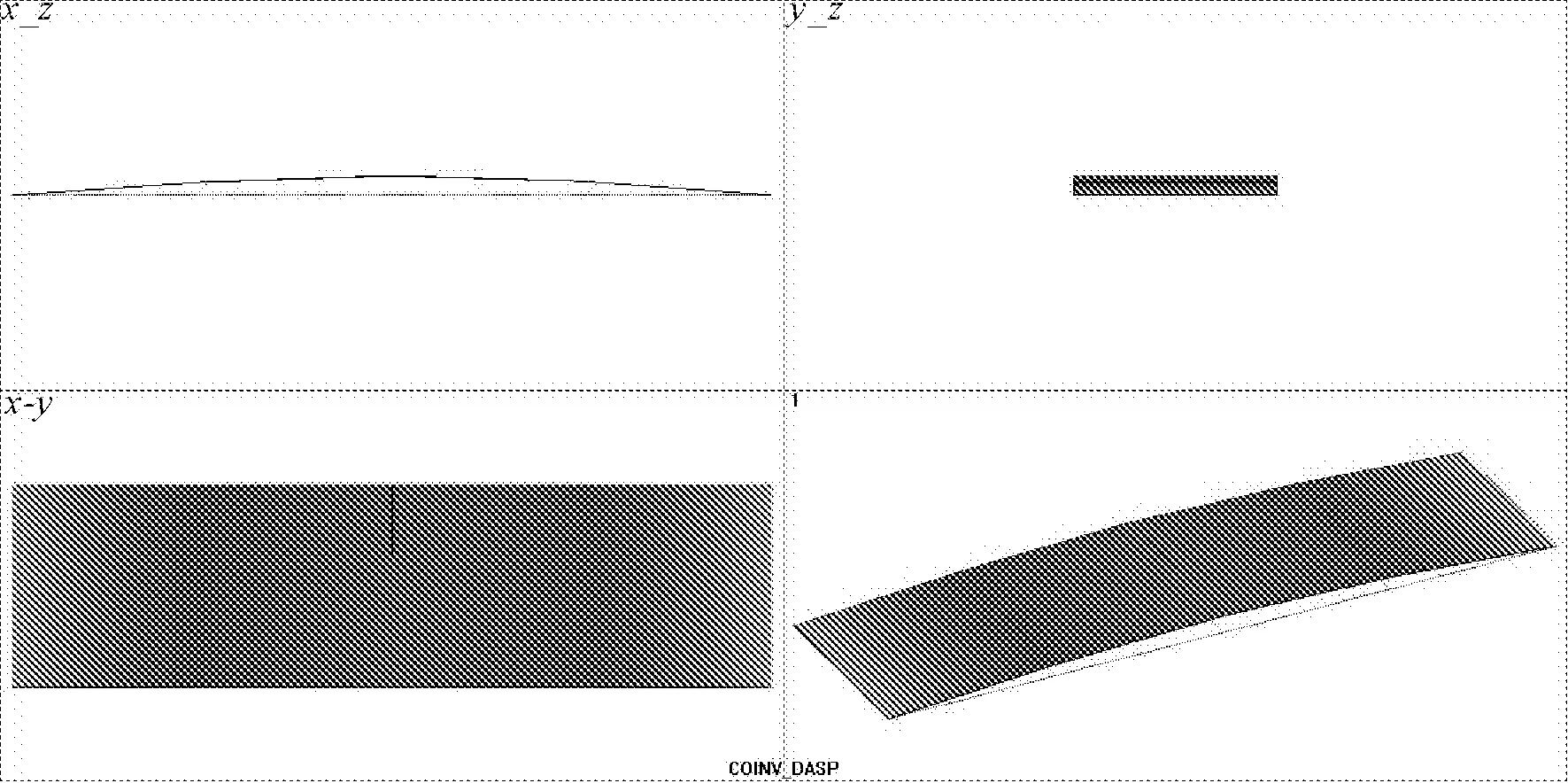
图9 一阶振型拟合图

由拟合图形可见，桥梁实测振型与理论计算振型相符。

3.4 结构冲击系数分析

本项目动应变的测试选取了主梁的跨中截面，在跨中钢主梁底板布设动应变测点，采集不同行车速度下各测点的动应变时程曲线，选取各行车速度下动应变幅值最大的测点进行冲击系数分析。分析图谱如图10所示。

图10 动应变时程曲线图

根据《公路桥涵设计通用规范》[17](JTG D60—2015)中关于冲击系数的确定方法，当结构基频1.5Hz≤f≤14Hz时，冲击系数应按式(2)确定：

1+μ=1+0.1767lnf-0.0157

(2)

式中：f为结构基频；1+μ为结构冲击系数。

由式(2)计算可得结构冲击系数为1.146。

不同车速下桥梁冲击系数实测值与理论值见表3。

表3 不同车速下桥梁冲击系数实测值与理论值的对比

从测试结果来看，结构实测冲击系数值与行车激励车速无显著关系，行车速度为40km/h时的实测冲击系数略大于理论值，为该桥重型货车最不利的行车速度，其余车速下实测冲击系数均小于理论值，说明该桥整体行车性能良好。

3.5 结构阻尼分析

阻尼比是表征桥梁结构耗散外部能量输入能力的参数，阻尼比大，说明桥梁耗散外部能量输入的能力强，反之亦然；但是，过大的阻尼比可能是桥梁结构存在开裂或支座工作不正常等现象引起，通常桥梁结构的阻尼比介于0.01～0.08之间。该桥阻尼比计算根据实测自由振动衰减曲线取值。

阻尼比计算按公式(3)：

(3)

式中：D为阻尼比；n为波数；Ai和Ai+n为n个波最初和最终的振幅。

不同激励车速下的桥梁阻尼比见表4。

表4 不同激励车速下实测桥梁阻尼比

从测试结果来看，实测桥梁阻尼比与激励车速无显著关系，该桥阻尼比介于0.011～0.014之间，在正常范围内，说明该桥无严重损伤，支座工作正常。

4 结 论

本文以该钢混叠合梁桥为工程背景，对其动力参数进行了有限元分析，并采用行车激励的方式对其动力性能进行了测试，采集分析了不同行车速度下结构的自振频率、振型、冲击系数及阻尼比，通过对比分析，得出以下结论：

(1) 行车激励能够有效的对被测桥梁起到激振作用，从而获取更高信噪比的响应信号。

(2) 不同车速的行车激励只是为了达到更好的激振效果，其车速与测试结果并无显著关系。

(3) 在数据后处理时准确选取自由振动曲线进行频谱分析可有效避免车桥耦合振动对测试结果的干扰。

(4) 该桥各动力参数测试结果无异常，桥梁结构动力性能良好，结构无较大损伤。

(5) 车速为40 km/h时实测冲击系数略大于理论值，为该桥重型货车的最不利车速。