基于主动倾斜转弯的超空泡航行器机动控制方法
宋书龙, 吕 瑞, 周景军, 万亚民, 李建辰
基于主动倾斜转弯的超空泡航行器机动控制方法
宋书龙1,2, 吕 瑞1, 周景军1, 万亚民1, 李建辰1
(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制重点实验室, 陕西 西安, 710077)
针对超空泡航行器采用传统方式机动能力不足的问题, 文中建立了一种基于主动倾斜转弯的机动控制方法。在分析超空泡航行器流体动力的基础上, 根据不同工况下航行器的沾湿情况, 求解了滑行力系数及力矩系数表格, 对滑行力进行了重构, 建立了超空泡航行器六自由度动力学模型, 基于极限操舵模式设计了超空泡航行器深度与横滚通道的比例-积分-微分控制器, 提出了基于主动倾斜转弯控制策略的横滚-航向协调控制的机动控制方法。数学仿真结果表明, 所设计的控制器动态性能良好, 可以满足超空泡航行器的机动要求。文中方法可为单自由度空化器超空泡航行器的机动实现问题提供参考。
超空泡航行器; 主动倾斜转弯; 动力学模型; 比例-积分-微分控制
0 引言
超空泡航行器通过通气的方式在航行器与水介质间产生气体薄膜, 极大地降低了航行阻力, 使其水下航行速度可以突破200 kn, 为水下减阻技术开辟了新的方向。然而, 正是其特殊的流体动力布局, 超空泡航行器极其不稳定, 目前各国主要针对直航超空泡航行器进行探索与研究, 机动型超空泡航行器的研制任重而道远。
从公开资料来看, 多数学者主要是研究超空泡航行器的定深控制, 而关于超空泡航行器水平面机动控制问题的文献鲜有发表。文献[1]分析比较了稳态状态下倾斜转弯方式与二自由度首舵转弯方式的机动能力; 文献[2]基于二自由度首舵控制方式研究了超空泡航行器的机动控制。文献[3]估算了以尾垂直舵机动方式的机动能力, 并指出尾垂直舵仅能对航行器进行航向修正而无法满足机动要求, 采用其他机动方式是机动型超空泡航行器的研究方向。文中参考航空航天倾斜转弯机动方式, 完成了基于主动倾斜转弯控制策略控制规律的设计, 即通过操差动舵控制航行器主动横滚, 使空化器产生水平分量的作用力, 以提供航行器需要的法向过载, 实现航行器的机动变向。
文中分析了超空泡航行器的流体动力, 完成了航行器六自由度动力学模型的构建, 针对尾部滑行力求解需实时计算空泡形态的问题, 参考航空航天中气动力参数获取方法, 根据不同工况下航行器的沾湿情况, 建立了采用查表插值法获取尾部滑行力的计算方法, 针对超空泡航行器尾偏航舵机动能力不足的问题, 提出了超空泡航行器基于主动倾斜转弯策略的横滚-偏航协调控制规律, 并通过仿真验证了动力学模型、控制规律的合理性。文中研究可为单自由度超空泡航行器的机动实现问题提供参考。
1 六自由度动力学模型
1.1 坐标系定义

图1 超空泡航行器坐标系示意图
1.2 超空泡航行器流体动力分析
假设航行器在航行过程中推力与阻力保持平衡[4-5], 因此文中不再计算航行器所受的阻力, 只考虑航行器纵向与侧向的力。
1) 空化器上的作用力
根据势流理论可知, 空化器上的作用力沿空化器盘面法线方向, 并指向空化器盘面, 作用点位于盘面中心, 空化器上的作用力可表示为

则空化器产生的力矩可表示为

2) 尾舵上的作用力
文中俯仰通道仅通过操控空化器实现, 尾部模型只有垂直舵, 尾垂直舵上的作用力可表示为[6]

则尾垂直舵产生的力矩可表示为

3) 尾部滑行力
Hassan给出的尾部滑行力计算公式[7]为

式中: 为航行器柱段半径; 为来流密度, 为滑行角; 分别为航行器尾端面沾湿深度和航行器沾湿长度; 为尾端面对应空泡截面半径, 且假设滑行力作用点位于距尾端面沾湿长度处。
则滑行力的分量可表示为

式中: 为接触角, 它是空泡偏移后航行器尾部中心与对应空泡截面中心的连线与轴的夹角, 如图3所示。
则滑行力矩可表示为

4) 重力

5) 滑行力重构
由于超空泡航行器尾部滑行力与空泡形态时刻相关, 要得到尾部滑行力需要计算各情况下的空泡形态, 参考航空航天中气动力参数的获取方法, 文中采用查表插值法实时获取超空泡航行器尾部滑行力及力矩, 即根据航行器不同攻角、舵角、侧滑角和回转角速度下航行器与空泡的位置耦合关系, 计算获得滑行力与力矩系数表格, 对滑行力进行重构, 在动力学模型求解过程中, 根据当前的运动参数通过对比系数表格, 可实时获取滑行力, 查表插值可通过自编函数或Matlab中interp2函数实现, 下面对滑行力重构过程进行说明。
a. 纵向滑行力重构
空化器攻角会使空泡发生变形, 轴线偏移量可通过下式计算[8]



图4 纵向滑行力示意图

图5 升力系数曲面


b. 侧向滑行力重构
图6 侧向滑行力示意图
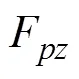

1.3 超空泡航行器六自由度动力学模型
通过上述超空泡航行器的流体动力分析, 根据动量定理、动量矩定理可得其六自由度动力学模型为

2 控制规律设计
由于受文章篇幅限制, 文中不再详述控制规律的推导过程, 这里仅给出控制器设计的具体步骤: 首先, 在小角度范围内对滑行力及力矩进行线性拟合, 获得线性化滑行力计算公式; 将该公式代入动力学模型, 推导出深度-首舵及横滚角-差动舵传递函数; 基于传递函数对深度、横滚角控制器的PID参数进行整定, 得到深度及横滚角的PID控制器。以升力系数为例, 根据不同攻角、首舵舵角计算的升力系数拟合值与理论值如图7所示, 可知拟合值与理论值吻合较好。

图7 升力系数拟合值与理论值对比
此外, 考虑到超空泡航行器对于控制作用的响应非常快, 对控制执行机构的快速性要求较高, 文中采用极限舵操舵方式对超空泡航行器纵向通道与横滚通道进行控制[9]。基于以上步骤得到的超空泡航行器控制规律如下。
1) 纵向通道控制规律
纵平面内深度控制规律为

当航行器横滚时, 首舵的作用力会在水平面产生分量, 其提供的升力减小, 此时以航行器无横滚时给出的首舵指令会相对较小, 因此给出考虑航行器横滚时的深度控制算法[10]为

2) 横滚通道控制规律
横滚通道控制规律为

3) 基于主动倾斜转弯的航向通道控制规律设计
若航行器深度与横滚能够实现稳定控制, 且一般情况下, 为了保证航行器深度的稳定, 首舵舵角始终保持朝下打舵, 即始终提供升力。当航行器横滚时, 首舵上的作用力将在水平方向产生分量, 其可以提供航行器机动所需的法向过载, 实现航行器的机动变向, 可知通过控制航行器的主动横滚便可以实现对航向的协调控制。
3 机动航行控制器仿真分析
初始条件: 初始航速100 m/s, 初始深度–6 m, 仿真时间6 s。期望指标: 期望深度保持–6 m不变, 0~1 s期望偏航角0°, 1~6 s期望偏航角20°。仿真结果及分析如下。
3.1 纵平面仿真
纵平面仿真结果如图8~图11所示。由图可知, 在控制器作用下, 攻角保持在-0.4°~0.6°, 整个控制过程中, 深度偏差有较小的振荡, 主要集中在主动横滚控制作用期间, 最大深度偏差为0.12 m, 可见深度通道的超调和振荡均在可接受的范围之内, 说明文中设计的纵向通道控制器针对超空泡航行器的深度控制是适用的。同时可以看到, 由于超空泡航行器特殊的流体动力布局及极限舵的操舵模式, 其振荡较为剧烈, 这对航行器的稳定航行有着不利影响, 在未来的工作中将开展此方面的研究。
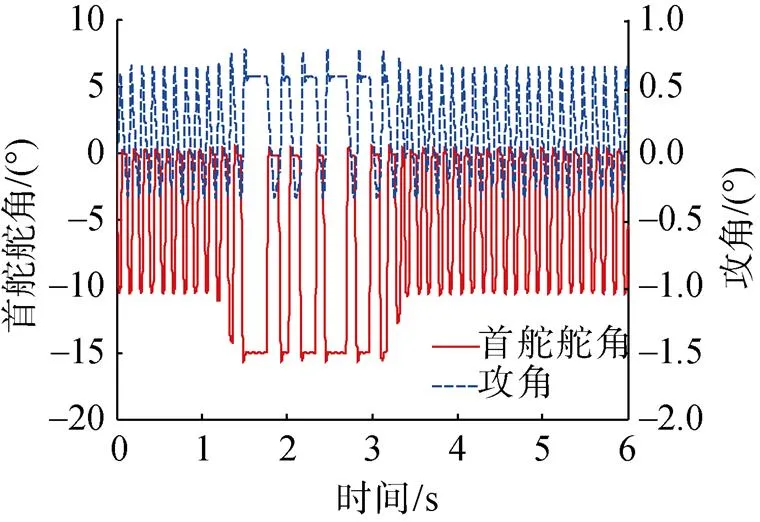
图8 首舵舵角和攻角随时间变化曲线
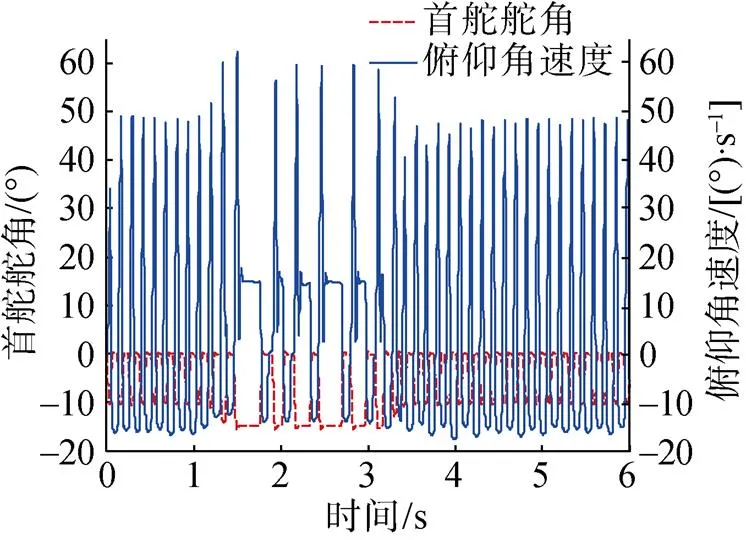
图9 首舵舵角和俯仰角速度随时间变化曲线

图10 首舵舵角和俯仰角随时间变化曲线
3.2 水平面仿真
水平面仿真结果如图12~图15所示。由图可知, 在控制器作用下, 侧滑角保持在-0.4°~0.4°以内, 在横滚角保持-60°的稳定时间段2~3 s内, 偏航角增加约10.46°, 可知回转角速度为10.46 °/s。同时注意到偏航角速度在1~1.5 s横滚角逐渐增大的情况下存在振荡, 对比期间首舵舵角变化曲线可知, 这是由首舵的极限操舵方式导致, 但总的来说主动倾斜转弯控制策略下偏航角无超调, 且偏航角的振荡在可接受的范围之内, 说明文中针对超空泡航行器设计的基于主动倾斜转弯的航向控制策略是有效的。
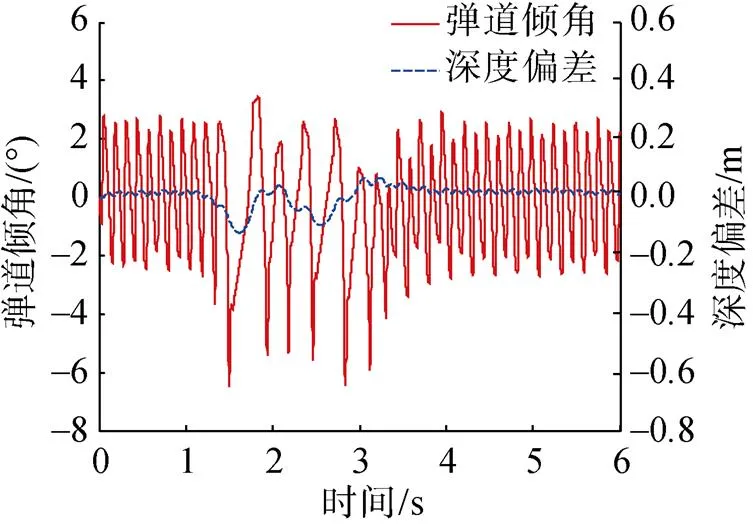
图11 弹道倾角和深度偏差随时间变化曲线

图12 差动舵舵角和侧滑角随时间变化曲线

图13 差动舵舵角和偏航角速度随时间变化曲线
3.3 横滚通道仿真


图14 差动舵舵角和偏航角随时间变化曲线
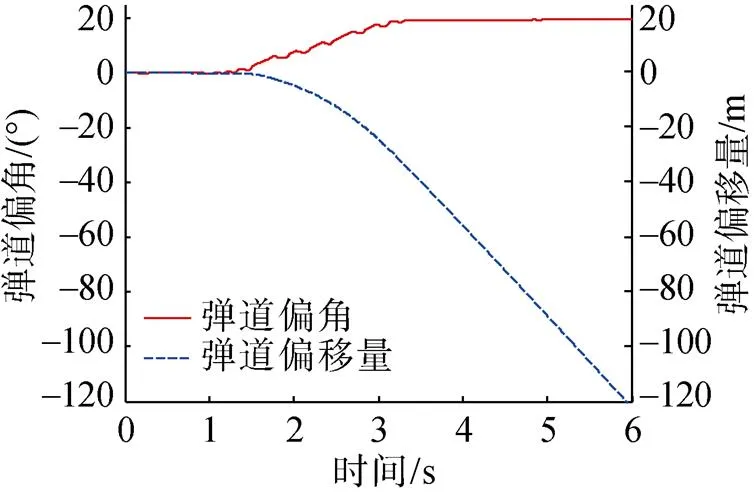
图15 弹道偏角和弹道偏移量随时间变化曲线

图16 差动舵舵角和横滚角速度随时间变化曲线

图17 差动舵舵角和横滚角随时间变化曲线

图18 超空泡航行器运动轨迹
4 结束语
文中针对超空泡航行机动变向问题, 提出了主动倾斜转弯的控制方法。首先分析了超空泡航行器的流体动力, 建立了采用查表插值法实时获得滑行力的计算方法, 基于PID控制算法完成了超空泡航行器纵向通道与横滚通道的控制规律设计, 首次建立了横滚-偏航协调控制的机动控制算法, 仿真结果表明, 超空泡航行器能够很快达到指令要求, 60°横滚角下, 超空泡航行器最大回转角速度可达10.45°/s, 所设计的控制器动态特性良好, 表明所设计的基于主动倾斜转弯的控制器是有效的。文中提出的基于主动倾斜转弯策略的横滚–偏航协调控制方法可为单自由度空化器超空泡航行器的机动实现问题提供参考。然而, 文中假定了航行器航行过程中阻力与推力保持平衡的理想条件, 未来研究中将针对该问题, 进一步完善动力学模型的构建。
[1] 蒋运华, 安伟光, 安海. 超空泡运动体水平面运动弹道特性研究[J]. 弹箭与制导学报, 2012, 32(6): 117-120. Jiang Yun-hua, An Wei-guang, An Hai. Kinematic Modeling and Trajectory Simuation for Underwater Supercavitating Vehicles[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(6): 117-120.
[2] 李代金, 罗凯, 党建军, 等. 超空泡水下航行器空间运动建模与弹道仿真[J]. 兵工学报, 2012, 33(8): 956-961. Li Dai-jin, Luo Kai, Dang Jian-jun, et al.Trajectory Characteristic Study of Supercavitating Vehicles Moving in Horizontal Plane[J]. Journal of Projectiles, Rockets, Missiles and Guidanc, 2012, 32(6): 117-120.
[3] 罗凯, 李代金, 黄闯. 超空泡航行技术的理论基础[M].北京: 科学出版社, 2016.
[4] Lin G, Balachandran B, Abed E H. Dynamics and Control of Supercavitating Vehicles[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(2): 021003.1- 021003.11.
[5] Van B, Bokor J, Balas G J, et al. Longitudinal Motion Control of a High-speed Supercavitation Vehicle[J]. Jour- nal of Vibration and Control, 2007, 13: 159-184.
[6] 张宇文, 袁绪龙, 邓飞. 超空泡航行器流体动力学[M].北京: 国防工业出版社, 2014.
[7] Hassan S E. Analysis of Hydrodynamic Planing Forces Associated with Cavity Riding Vehicles[R]. USA: NU WC-NOT Technical Memorandum, 2004.
[8] Logvinovich G V. Hydrodynamics of Flows with Free Boundaries. Kiev[M]. Russian: Naukova Dumka Publishing House, 1969.
[9] 李雨田, 张宇文, 刘立栋, 等. 水下超空泡航行器巡航段稳定控制[J]. 弹道学报, 2012, 24(1): 92-96. Li Yu-tian, Zhang Yu-wen, Liu Li-dong, et al. Cruise Phase Stability Control for Underwater Supercavitating Vehicle[J]. Journal of Ballistics, 2012, 24(1): 92-96.
[10] 郝哲, 张秦南, 王立文, 等. 一种基于矢量原理的三通道精确控制算法[J]. 鱼雷技术, 2014, 22(2): 110-114. Hao Zhe, Zhang Qing-nan, Wang Li-wen, et al. A Three-Channel Accurate Control Algorithm Based on Vector Principle[J]. Torpedo Technology, 2014, 22(2): 110-114.
Maneuver Control Method of Supercavity Vehicle Based on Active Bank-To-Turn
SONG Shu-long1,2, LÜ Rui1, ZHOU Jing-jun1, WAN Ya-min1, LI Jian-chen1
(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi’an 710077, China)
To raise the mobility of the supercavity vehicle, a maneuver control method based on active bank-to-turn(BTT) is established in this paper. After analyzing the hydrodynamics of the supercavity vehicle, the gliding force coefficient and moment coefficient tables are solved according to the wetting status of the vehicle under different working conditions, and the sliding force is reconstructed. A six-degree-of-freedom dynamic model of the supercavity vehicle is established. According to the up-and-down rudder control mode, the proportional-integral-derivative(PID) controller of depth and roll channel of the supercavity vehicle is designed. Thus, a maneuver control method based on the active BTT control strategy is proposed. Mathematical simulation results show that the designed controller has good dynamic characteristics, and can meet the requirements of the supercavity vehicle for maneuver. The method established in this paper can be referenced for maneuver realization of supercavity vehicle with single-degree-of-freedom cavitator.
supercavity vehicle; active banking strategy; dynamic model; proportional-integral-derivative(PID) control
TJ630.1; TB71.2
A
2096-3920(2019)06-0607-07
10.11993/j.issn.2096-3920.2019.06.002
2016-11-09;
2016-12-18.
万人计划青年拔尖人才项目(W03070206); 装备预研共用技术项目(41407040101); 国重预研基金项目(JCKY2019207CD01).
宋书龙(1994-), 男,助工, 主要研究方向为总体技术.
宋书龙, 吕瑞, 周景军, 等. 基于主动倾斜转弯的超空泡航行器机动控制方法[J]. 水下无人系统学报, 2019, 27(6): 607-613.
(责任编辑: 陈 曦)

