装药深度及空气域尺寸对水下爆炸的影响分析
刘世聪, 王秋生, 娄浩然
装药深度及空气域尺寸对水下爆炸的影响分析
刘世聪, 王秋生, 娄浩然
(北京工业大学 建筑工程学院, 北京, 100124)
在水下爆炸试验中, 很难开展针对装药深度及影响数值计算精度的空气域尺寸研究, 因此, 数值仿真就成为研究水下爆炸的重要手段。文中基于离心机水下爆炸试验, 利用二维、三维模型对超重力场下的球形炸药水下爆炸进行仿真, 并与试验结果进行对比, 验证了所建模型的合理性。在2个模型的基础上, 同时建立具有不同装药深度及空气域尺寸的模型, 以研究两者对水下爆炸冲击波及气泡脉动数值仿真结果的影响。研究表明: 装药深度越大, 距离炸药中心相同测距处的冲击波峰值越大, 但峰值随装药深度的增幅并不明显; 空气域尺寸大小对水下爆炸气泡脉动计算影响也很小。
水下爆炸; 数值仿真; 装药深度; 空气域尺寸
0 引言
水下爆炸在军事国防及民用建设领域都具有广泛用途。水下爆炸载荷主要包括冲击波和气泡脉动两部分, 两者大约各占爆炸总能量的50%[1]。试验作为最早被采用的研究手段, 在研究初期, 多集中于原型[2-4]及机理试验[5-8], 但大多数的原型试验操作难、安全性低, 机理试验又忽略重力和浮力等因素, 因此很难获得理想的研究效果。大量在离心机中进行的土中爆炸成坑试验为水下爆炸研究提供了很好的思路[9-10]。目前, 国内外针对离心机水下爆炸试验开展得较少, 中国水利水电科学研究院在该领域做出了初步探索[11-15], 验证了离心机试验的可行性, 并总结了一些水下爆炸冲击波及气泡脉动规律。
随着科学技术的进步, 数值仿真已成为研究水下爆炸的重要手段, 通过仿真可以模拟很多试验条件下无法进行的工况, 这为爆炸试验的开展与进行提供了良好的技术支持。例如针对装药深度的研究便是数值仿真重要的应用之一, 不同的装药深度对目标结构会产生不同的毁伤效果, 有必要进行深入研究。王树乐等[16]利用Abaqus有限元软件总结了不同爆源深度对靶船的破坏特点, 为今后研究舰船的抗毁伤提供了很好的参考。徐豫新等[17]利用Autodyn有限元软件对不同水深处的一维炸药爆炸进行了仿真, 研究得出冲击波受装药深度影响较小, 而气泡脉动受其影响较大。此外, 在水下爆炸仿真中, 由于计算机能力的限制, 计算区域往往不能无限增大, 但模型建立必须吻合试验工况, 这就给仿真带来很大困难。由于水下爆炸的研究集中于水域, 因此, 对特定水下爆炸试验进行数值仿真时, 有效控制空气计算域尺寸不仅可以大大缩短计算时间, 同时又可以达到计算结果所要求的精度。国内针对空气域尺寸对水下爆炸影响的研究较少。徐豫新等[17]通过一维轴对称模型研究了计算区域对气泡脉动的影响, 结果表明, 计算区域越小, 第1次气泡最大半径越小。目前针对装药深度的研究大都缺少试验背景的支持, 其研究结果不具备很好的适用性。此外, 大部分研究者都将研究重点放在水下, 对于空气域的研究相对较少。
基于此, 文中利用与离心机水下爆炸试验结果吻合较好的二维、三维模型, 建立多工况数值仿真计算, 并对比研究了装药深度及空气域尺寸对水下爆炸冲击波及气泡脉动仿真结果的影响。
1 离心机水下爆炸试验
在中国水利水电科学研究院试验室进行的离心机水下爆炸试验[11, 15]是文中应用的试验基础。离心机水下爆炸试验是缩比模型试验的一种, 其利用离心机设备使固定于离心机箱中的模型箱发生转动, 忽略竖直方向自然重力加速度的影响并假设离心机转动速率不变, 最终会形成沿转臂方向、比自然重力加速度大倍的离心加速度, 同时在模型箱中形成超重力场, 实现小当量炸药模拟大当量炸药的爆炸效果。离心机水下爆炸试验是以相似理论[18]为理论基础。文献[11]对相似理论进行了详细的论述, 同时也验证了相似理论在试验条件下的可行性。离心机设备示意图如图1所示。图2为离心机箱中的模型箱内部图。

图1 离心机示意图

图2 试验模型箱内部图
图2中, 模型箱内部尺寸为1080 mm×720 mm ×700 mm, 箱内部水体的深度为600 mm, 侧向布置高速摄像机以捕捉水下爆炸气泡。试验分别在超重力环境20, 30, 40和50下进行。炸药采用质量为1 g的黑索金(RDX)球形炸药, 半径R为5.25 mm, 密度为1.65 g/cm3。将炸药分别置于水下200, 300 mm处, 在纵向相同深度处安装水压力传感器, 设置爆距(炸药与传感器间的距离)分别为175, 250, 300, 350 mm。
表1列出了离心机水下爆炸试验工况。表中:为炸药质量;为装药深度;为爆距;P为此工况下的冲击波峰值压力;R为最大气泡半径;为气泡脉动周期。

表1 试验工况
2 超重力场水下爆炸数值仿真
2.1 状态方程
空气采用理想气体状态方程, 而理想气体状态方程为线性多项式状态方程[12]的特殊形式。用线性多项式状态方程表示的压力
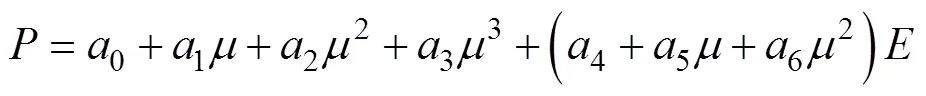
式中:为水的压缩比,/0-1,0为水的初始密度,01.0 g/cm3,为水的当前密度;为比内能;1,2,3,4,5和6为多项式系数, 由于水下爆炸中的空气处于膨胀状态, 因而当<0时,2=6=0, 同时令1=3=0,4=5=-1, 可得空气的理想气体状态方程

式中:为绝热指数, 取1.4; 空气初始密度0取1.225 kg/m3。
RDX炸药采用JWL(Jones-Wilkins-Lee)状态方程[19]

式中:,,1,2和为JWL状态方程参数;为自然常数;为爆轰产物的相对体积;为炸药的初始比内能。试验所用的炸药是专业研制的, 因此利用文献[15]所介绍的半经验方法确定JWL状态方程中的各参数。
炸药爆速与装药密度的关系由下式给出[20]
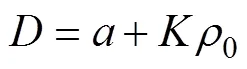
式中:为炸药爆速;0为炸药初始密度;和为与炸药种类相关的经验系数。对于RDX炸药,=2.395,=3.589[20]。由RDX炸药初始密度0= 1.65 g/cm3, 可得炸药爆速=8.317 km/s。
由及0可得单位体积炸药的初始比内能0[21]和爆轰产物的绝热指数[22], 即


JWL状态方程对应的等熵线方程为

式中:为待定系数; 下标代表等熵过程。
结合热力学关系, 得出等熵线上内能


式中,CJ为CJ点处爆轰产物的相对比容。

式中,CJ为炸药的爆压。
由爆轰产物Hugoniot关系式得

式中:取值0.33[23];2≈ 0.271[23]; 4≤1≤5[24-25]。
CJ和CJ可表示为


联立式(11)~式(13)可求出,,。综合各式得各参数取值:=565.295 GPa,=1.21711 GPa,1= 4.213 9,2=1.137 75,=0.35,0=9.536 GJ/m3。
水体采用Shock状态方程[19], 其形式为

因为在水下爆炸中假定水是不可压缩的, 所以冲击波速度与波后质点速度u的关系应取压缩量>(压缩量限值, 取0)的情况, 即
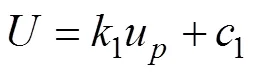
且
E-Navigation战略自提出以来进展并不顺利,主要原因是通信问题没有解决。E-Navigation战略旨在发展海上信息的一体化,船舶可获取海上更多有价值的信息。船舶可通过外界广域网获取卫星播发的信息、陆地传输的信息和附近船舶播发的感知信息,同时船舶还可通过使用自身装配的设备感知自身及环境信息,并以局域网的形式在本船内部分发。为使船舶获得实时的船舶及水文气象资料信息,应从获取信息的方式入手,即提升卫星通信速度(带宽)、降低卫星通信价格、更新岸基设施和海上在航船舶的通信系统以及提高船舶感知能力,从而保障航行安全和保护海洋环境。E-Navigation战略发展需要通信技术予以整体贯通见图1。


式中: Г为Grüneisen系数, 取0.28;为水的初始比内能;1和1分别为冲击波速度与水中质点速度u成线性关系时的斜率与常数项, 为经验系数, 取1=1.75,1=1.483×103m/s。
2.2 数值仿真模型
依据离心机水下爆炸试验, 分别建立如图3和图4所示的二维模型NUM-2D、三维模型NUM- 3D进行水下爆炸数值仿真研究。二维模型精度高, 主要用来对历经时间短的冲击波进行研究; 三维模型具有低维计算结果到高维模型映射的功能, 可以大大缩短计算时间, 因此用来研究历经时间长的气泡脉动。

图3 二维模型NUM-2D
图3中, 二维模型NUM-2D采用轴对称方式建立, 质量1 g, 半径5.25 mm的炸药位于水下300 mm处, 同离心机水下爆炸试验一样, 在与炸药相同深度处布置测点, 爆距分别为175, 250, 300, 350 mm, 同时从测点5开始, 每50 mm布置1个测点。水体、炸药和空气均采用Euler单元体建立, 水体尺寸为700 mm×600 mm, 空气域尺寸为700 mm×100 mm, 其高度同试验模型箱中的空气部分一致, 在人工截断边界处(空气顶端)施加流出边界, 以刚性边界模拟试验的模型箱, 其中刚性边界同试验模型箱一致, 尺寸为700 mm×700 mm。文献[15]对模型的网格尺寸进行了初步的敏感性分析, 所以依据此文, 二维模型的计算网格尺寸取0.5 mm。

图4 三维模型NUM-3D
Fig. 4 Three-dimensional model NUM-3D
如图4所示, 三维模型NUM-3D采用面对称方式建立, 将二维模型中冲击波刚要碰触边界时的计算结果映射到三维模型中继续计算。炸药位于水下300 mm处。水体、炸药和空气均采用Euler单元体建立。依据离心机水下爆炸试验工况, 三维模型中水体尺寸为1 000 mm×600 mm×350 mm, 空气域尺寸为1 000 mm×100 mm×350 mm, 空气高度同试验模型箱中的空气部分一致, 除对称面及空气顶端的流出边界外, 其余面均用刚性边界模拟试验模型箱, 刚性边界同试验模型箱尺寸一致, 即1 000 mm×350 mm×700 mm。同样根据文献[15], 三维模型的计算网格尺寸取5 mm。
3 仿真结果与分析
3.1 离心机水下爆炸试验验证
离心机水下爆炸试验结果验证了Cole[2]和Gel’Fand等[26]的结论: 1) 研究冲击波峰值时可以忽略重力影响; 2) 气泡脉动必须考虑重力作用, 且随着重力加速度的增大, 气泡最大半径R以及脉动周期都在减小。文中利用2.2节中提到的2个数值仿真模型对试验进行仿真, 以此验证上述两者的合理性。
水压力传感器测得的试验不同工况及相对应的数值仿真所得的冲击波压力波形如图5所示, 因为在数值仿真过程中设置了偏小的人工粘性系数, 从而引起了冲击波波后出现伪振荡[27]。表2为P数值计算值同试验值之间的相对误差。

图5 不同试验工况下冲击波压力随时间变化曲线
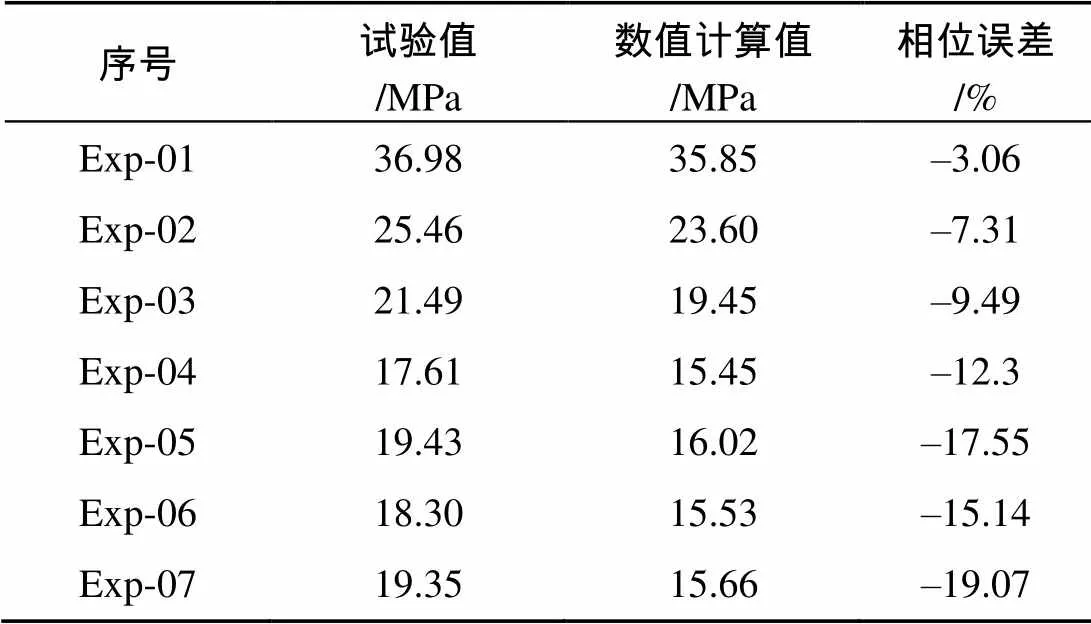
表2 不同试验工况下冲击波压力峰值
从图5及表2可以看出, 随着爆距的增大, 冲击波峰值P逐渐减小, Exp-04~07是在相同药量、不同重力加速度下进行的不同试验工况, 但四者的冲击波波型基本一致, 且峰值压力P也接近, 这样便验证了二维模型NUM-2D的合理性。
图6展示了Exp-04~07与4种试验工况所对应的数值仿真结果的对比, 各重力加速度下数值计算的气泡最大半径R以及脉动周期如表3所示, 可见数值计算得到的R和与各自的试验值误差均较小, 都在3%以内, 且变化趋势也与试验值一致。但在气泡收缩阶段, 气泡半径曲线逐渐偏离试验结果, 这主要是由于试验过程中能量损失相比数值计算大, 且数值计算时网格尺寸存在差异等多种因素导致的。

图6 试验与数值气泡半径随时间的变化曲线

表3 各重力条件下气泡最大半径及脉动周期试验结果与数值仿真结果对比
从图6及表3中可知, 数值仿真和试验呈现同样的规律, 即Cole[2], Gel’fand等[26]的结论, 气泡脉动必须考虑重力作用, 且随着重力加速度的增大,R和都呈减小趋势。这样便验证了三维模型NUM-3D的合理性。
3.2 影响因素分析
3.2.1 装药深度分析
由表1可知, Exp-03、Exp-08分别为40重力加速度下, 炸药处于水下200, 300 mm时的试验工况, 两者只记录了爆距=300 mm时的冲击波峰值压力。可见, 装药深度越大, 相同测距处测得的P越大。但由于试验条件的限制, 针对的研究只有2组, 因此难以说明对冲击波的影响, 因此文中利用数值仿真的方法对比进行了研究。
图7为不同装药深度的二维计算模型示意图。该图只表示了装药深度为100, 300 mm时的工况, 其余工况除装药深度外, 均与图7一致。

图7 不同装药深度的二维数值计算模型
在二维模型NUM-2D中, 沿其对称轴将炸药分别置于水下100, 200, 300, 400和500 mm, 同时在与炸药相同深度处横向布置测点, 为了使文中的结论更具代表性, 除了布置2.2节中的11个测点外, 在爆距=20~160 mm之间, 每隔20 mm布置1个测点, 通过多测点数值计算结果来研究对P的影响。
表4为不同装药深度下各测点的P。由表4可以看出, 当<300 mm(测点3)时, 随着的增加, 相同值下的P虽有所增加, 但各深度处的增幅均不超过3%; 当300 mm<<450 mm(测点6)时, 随着的增大, 由于计算误差及四周边界条件的影响, 有个别点的P已经不再增加, 但总体仍呈微弱增长的趋势; 当>450 mm时, 由于模型计算尺寸的限制, 峰值已经开始受到边界的明显影响, 各峰值之间的误差也很大。如表1所示, Exp-03和Exp-08为相同爆距不同装药深度的对比试验工况, 两者之间的增幅仅为0.94%, 可以认为, 冲击波峰值P随着的增加而增加, 但增加趋势并不明显。
2.3.2 空气域尺寸
由离心机水下爆炸试验也可以看出, 模型箱内的水域是有限的, 而空气域是无限的, 若依据试验条件建立对应的空气域, 不仅受计算网格尺寸的影响, 同时其过大的尺寸也会大大增加数值仿真的计算时间。因此, 文中通过改变空气域尺寸研究其对气泡脉动数值计算结果的影响。
图8(a)在三维模型NUM-3D的基础之上, 将空气域加高了200 mm, 除前100 mm的空气域侧面为刚性边界, 用来模拟试验模型箱外, 其余超出部分的侧面全为流出边界; 图8(b)在三维模型NUM-3D的基础之上, 将空气域加高了500 mm; 图8(c)在图8(b)基础之上, 将空气域横向加宽了2000 mm, 均匀布置在图8(c)两侧, 多加的空气域边界全部设置为流出边界; 图8(d)是在图8(c)的基础上, 将空气域加高了600 mm。在建模过程中, 图8(a)~图8(c)的空气与水体是1个完整的有限元模型, 将所有材料填充到同一个模型里, 而图8(d)由于模型尺寸过大, 所以利用有限元软件的joint功能[17], 在图8(c)模型的基础上, 将3个独立的空气域添加到图8(c)模型上而成。如表5所示, 虽然5个模型拥有不同尺寸的空气计算域, 但他们计算出的气泡最大半径R相差不大, 计算出的脉动周期一致, 因此, 空气域尺寸的不同对气泡脉动计算结果影响很小。又由于随着空气域尺寸的增加, 数值仿真计算时间也会大幅增加, 因此, 若利用三维模型研究水下爆炸气泡脉动, 建议根据模型大小控制空气域尺寸, 以达到计算精度与计算时间的平衡。

表4 不同装药深度下各测点冲击波峰值


表5 不同空气域尺寸计算的气泡最大半径和气泡周期
4 结论
针对试验难度较大的水下爆炸装药深度研究及影响数值计算精度的空气域尺寸, 文中基于离心机水下爆炸试验背景, 运用数值仿真研究了两者对冲击波及气泡脉动的影响, 得出以下结论:
1) 装药深度越大, 距离炸药中心相同测距处的冲击波峰值越大, 但随深度增幅不大;
2) 空气域尺寸的不同对水下爆炸气泡脉动数值计算结果影响不大, 建议若利用三维模型研究水下爆炸气泡脉动, 应尽量控制空气域的尺寸, 以便实现计算精度与计算时间的平衡。
文中仅进行了数值计算结果与相应的误差分析, 对于这些研究结果背后的力学机理分析尚有待深入研究。
[1] Snay H G. Hydrodynamics of Underwater Explosions[C] //Symposium on Naval Hydrodynamics 1st, Washiton D C, USA. 1956: 325-352.
[2] Cole R H. Underwater Explosions[M]. New Jersey: Prin- ceton University Press, 1948.
[3] Brett J M, Buckland M, Turner T, et al. An Experimental Facility for Imaging of Medium Scale Underwater Explosions DSTO-TR-1432[R]. Australian: Defence Science and Technology Organisation, 2003.
[4] 黄超, 汪斌, 姚熊亮, 等. 试验室尺度水下爆炸气泡试验方法[J]. 传感器与微系统, 2011, 30(12): 75-77, 81.Huang Chao, Wang Bin, Yao Xiong-liang, et al. Laboratory-scale Underwater Explosion Bubble Experiment Met- hod[J]. Transducer and Microsystem Technologies, 2011, 30(12): 75-77, 81.
[5] Benjamin T B, Ellis A T. The Collapse of Cavitation Bubbles and the Pressures Thereby Produced Against Solid Boundaries[J]. Philosophical Transactions of the Royal Society of London, 1966, 260(1110): 221-240.
[6] Tomita Y, Shima A, Takahashi K. The Collapse of a Gas Bubble Attached to a Solid Wall by a Shock Wave and the Induced Impact Pressure[J]. American Society of Mech- anical Engineers, 1983, 105(3): 341-347.
[7] Zhang A M, Li S, Cui J, et al. Study on Splitting of a Toroidal Bubble Near a Rigid Boundary[J]. Physics of Fluids, 2015, 27(6): 062102.
[8] 张阿漫, 王超, 王诗平, 等.气泡与自由液面相互作用的试验研究[J]. 物理学报, 2012, 61(8): 1-13.Zhang A-man, Wang Chao, Wang Shi-ping, et al. Exp- erimental Study of Interaction Between Bubble and Fr- ee Surface[J]. Acta Physica Sinica, 2012, 61(8): 1-13.
[9] 范一锴, 陈祖煜, 梁向前, 等. 砂中爆炸成坑的离心模型试验分析方法比较[J]. 岩石力学与工程学报, 2011, 30(S2): 4123-4128.Fan Yi-kai, Chen Zu-yu, Liang Xiang-qian, et al. Comp- arison of Three Methods for Geotechnical Centrifuge Model Tests of Explosion Cratering Sand[J]. Chinese Jo- urnal of Rock Mechanics and Engineering, 2011, 30(S2): 4123-4128.
[10] Holsapple K A, Schmidt R M. On the Scaling of Crater Dimensions 1. Explosive Processes[J]. Journal of Geo- physical Research Atmospheres, 1980, 85(B12): 7247- 7256.
[11] Hu J, Chen Z Y, Wang Q S, et al. Underwater Explosion in Centrifuge PartⅠ: Validation and Calibration of Scaling Law[J]. Science China Technological Sciences, 2017, 60 (11): 1638-1657.
[12] Long Y, Zhou H Y, Liang X Q, et al. Underwater Explosion in Centrifuge Part II: Dynamic Responses of Defensive Steel Plate[J]. Science China Technological Sciences, 2017, 60(12): 1941-1957.
[13] Wu J Y, Long Y, Zhong M S, et al. Centrifuge Experiment and Numerical Study on the Dynamic Response of Air- backed Plate to Underwater Explosion[J]. Journal of Vibroengineering, 2017, 19(7): 5231-5247.
[14] Song G, Chen Z Y, Long Y, et al. Experiment and Numerical Investigation of the Centrifugal Model for Underwater Explosion Shock Wave and Bubble Pulsation[J], Ocean Engineering, 2017, 142(15): 523-531.
[15] 娄浩然, 胡晶, 梁向前, 等. 超重力场下球形炸药水下爆炸试验及数值模拟[J]. 工程爆破, 2017, 23(3): 15- 21.Lou Hao-ran, Hu Jing, Liang Xiang-qian, et al. Underwater Explosion Experiment and Numerical Simulation of Spherical Explosives Under Hypergravity Field[J]. Engineering Blasting, 2017, 23(3): 15-21.
[16] 王树乐, 陈高杰, 沈晓乐, 等. 基于并行计算的某战斗部中近场毁伤能力仿真研究[J]. 兵工学报, 2015, 36(S1): 298-302.Wang Shu-le, Chen Gao-jie, Shen Xiao-le, et al. A Num- erical Study of Warhead Damage Based on Parallel Computing in Near-field[J]. Acta Armamentarh, 2015, 36(S1): 298-302.
[17] 徐豫新, 王树山, 李园. 水下爆炸数值仿真研究[J]. 弹箭与制导学报, 2009, 29(6): 95-97, 102.Xu Yu-xin, Wang Shu-shan, Li Yuan. Study on Numerical Simulation of The Underwater explosion[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(6): 95-97, 102.
[18] 张效慈. 水下爆炸试验相似准则[J]. 船舶力学, 2007, 11(1): 108-118.Zhang Xiao-ci. Similarity Criteria for Experiment of Underwater Explosion[J]. Journal of Ship Mechanics, 2007, 11(1): 108-118.
[19] Century Dynamic Inc. AUTODYN Theory Manual Version 4.3[M]. USA: Century Dynamic Inc, 2005.
[20] 韩早, 王伯良. 混合炸药爆速的新方法[J]. 爆炸与冲击, 2014, 34(4): 421-426.Han Zao, Wang Bo-liang. A New Method for Predicting Detonation Velocity of Composite Explosive[J]. Explo- sion and Shock Waves, 2014, 34(4): 421-426.
[21] Johansson C H, Persson P A. Density and Pressure in the Chapman-Jouguet Plane as Functions of Initial Density of Explosives[J]. Nature, 1996, 212(5067): 1230-1231.
[22] Urtiew P A, Hayes B. Parametric Study of the Dynamic JWL-EOS for Detonation Products[J]. Combustion, Expl- osion, and Shock Waves. 1991, 27(4): 505-514.
[23] Urtiew P A, Hayes B. Parametric Study of the Dynamic JWL EOS for Detonation Products[J]. Combustion Explo- sion and Shock Waves, 1991, 27(4): 504-514.
[24] 孙承纬, 卫玉章, 周之奎. 应用爆轰物理[M]. 北京: 国防工业出版社, 2000.
[25] Urtiew P A, Hayes B. Empirical Estimate of Detonation Parameters in Condensed Explosives[J]. Journal of Energetic Materials, 1991, 9(4): 297-318.
[26] Gel'fand B E, Takayama K. Similarity Criteria for Underwater Explosions[J]. Combustion Explosion & Shock Waves, 2004, 40(2): 214-218.
[27] 杨坤, 陈朗, 伍俊英, 等. 计算网格与人工粘性系数对炸药水中爆炸数值模拟计算的影响分析[J]. 兵工学报, 2014, 35(S2): 237-243. Yang Kun, Chen Lang, Wu Jun-ying, et al. The Effects of Computing Grid and Artificial Viscosity Coefficient on Underwater Explosion Numerical Simulation[J]. Acta Armamenth, 2014, 35(S2): 237-243.
Effects of Charge Depth and Air Domain Size on Underwater Explosion
LIU Shi-cong, WANG Qiu-sheng, LOU Hao-ran
(College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)
In underwater explosion test, it is difficult to carry out research on the charge depth and the air domain size which affects the accuracy of numerical calculation. In this paper, based on the underwater explosion test of centrifuge, underwater explosion of spherical explosive under super-gravity field is simulated using two-dimensional and three-dimensional models, and the simulation results are compared with the test data to verify the rationality of the two models. Then, different charge depth and air domain size are added to the two models to analyze the effects of the two factors on simulation results of underwater explosion shock wave and bubble pulsation. The simulation results show that the greater the charge depth, the larger the shock wave peak values at the same distance from the center of the explosive, but the increase rate of the peak value with the charge depth is small; and the air domain size has little effect on numerical results of the underwater explosion bubble pulsation.
underwater explosion; numerical simulation; charge depth; air domain size
TJ630; TV542.5
A
2096-3920(2019)06-0664-09
10.11993/j.issn.2096-3920.2019.06.010
刘世聪, 王秋生, 娄浩然. 装药深度及空气域尺寸对水下爆炸的影响分析[J]. 水下无人系统学报, 2019, 27(6): 664-672.
2019-04-12;
2019-05-16.
国家自然科学基金重点资助项目(51339006); 北京市科委重点项目资助(Z161100002216001).
刘世聪(1993-), 男, 硕士, 主要研究方向为水下爆炸研究.
(责任编辑: 杨力军)

