枪械可靠性试验统计方案与参数估计研究

柳吉龄，闫培新，任 意，张洪彬，黄 亮，饶永红

（解放军63936 部队，北京 102202）

0 引言

枪械可靠性试验与评定是对枪械可靠性进行研究、分析和评价的一种手段，目的是确认其是否符合规定的可靠性定量要求，发现薄弱环节及提供可靠性信息，为改善其战备完好性、提高任务成功性、减少维修费用及保障费用提供支撑［1］。

本文研究了枪械可靠性的概念、各特征量的定义及其关系。针对枪械特性及其使用特点，对其故障分布规律进行了建模研究和特征分析，说明可以用指数分布来近似；由于指数分布便于工程应用，因此，以指数分布为基础，运用可靠性工程理论，结合数学方法，研究了定时截尾和序贯截尾两类试验统计方案，提出了试验样品数，试验时间（射弹发数）、合格判据等试验要素的量化确定方法；为定时截尾试验提出了枪械可靠性常用特征量故障率的点估计与区间估计公式，以便于量化把握枪械的可靠性特征；举例说明了枪械可靠性各试验统计方案与参数估计的应用方法，检验了其可行性、一致性和有效性。本文研究内容为系统规范地开展枪械可靠性试验与评定提供了理论支撑和实用范例。

1 枪械可靠性相关概念

1.1 枪械可靠性定义

枪械可靠性定义为：枪械在规定的条件下和规定的射弹数内，完成规定功能的能力。它是反映枪械耐用和可靠程度、无故障完成任务的一种能力。可靠性是用时间尺度来描述的质量特性，是指一个产品从使用时开始，随着时间的推移，能否稳定保持原有功能的性能。可靠性和时间紧密联系在一起，如果产品可靠性高，就意味着寿命长、故障少，所以离开时间就无可靠性而言。可靠性定义中规定的时间，是可靠性区别于产品其他特性的重要特征，一般是指所要求的任务时间，如长度、次数、里程、射击弹数等，对枪械而言，这里所说的时间就是指射弹量，以发为单位［2］。

1.2 枪械可靠性特征量

枪械可靠性特征量是用来表示枪械产品总体可靠性高低的各种可靠性数量指标的总称。可靠性特征可以采取平均故障间隔时间MTBF、累积故障概率F（t）、故障概率密度f（t）、可靠度R（t）、故障率λ（t）等参数作为特征量［1-8］。

1）MTBF 指可修复产品两次相邻故障之间的平均时间。枪械MTBF 的观测值为在规定条件和规定射弹量内枪械寿命单位总数与故障总数之比：

2）累积故障概率指枪械在规定的条件下和规定的射弹数内，未完成规定功能（即发生故障）的概率，也称为故障分布函数：

式中，f（t）为故障概率密度函数。

3）故障概率密度指枪械在射弹t 发后的单位时间里发生故障的概率，也就是累积故障概率对时间的变化率：

4）可靠度指枪械射弹t 发时的无故障概率，称为可靠度函数。由于枪械在规定的射弹数内发生故障的概率为累计故障概率，所以可靠度为：

5）故障率为射弹到t 发时尚未发生故障的枪械在该时间后单位时间内发生故障的概率，也称为失效率或故障率函数：

故障率的观测值为在规定条件和规定射弹量内，产品的故障总数与寿命单位总数之比：

可靠性各特征量之间的关系如图1 所示。

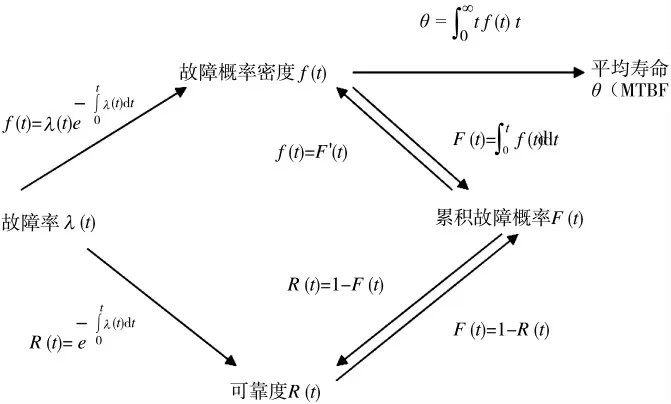
图1 可靠性特征量关系图

由图1 可见，可靠性特征量的这几个基本参数，只要知道其中一个，所有参数均可求得。可靠性特征量中故障分布规律研究是选取可靠性试验统计方案的基础。

1.3 枪械故障分布规律

目前国内外大多数可靠性标准中可靠性试验方案的选取建立在指数分布基础之上［7，9］，为了依据这些标准进行试验，首先要研究枪械的故障分布规律。这就需要根据枪械的可靠性试验数据，建立其可靠性数学模型［2，5，10-12］。如某型枪械可靠性指数分布的皮尔逊检验计算表如下页表1 所示。

表1 某型枪械可靠性指数分布皮尔逊检验计算表

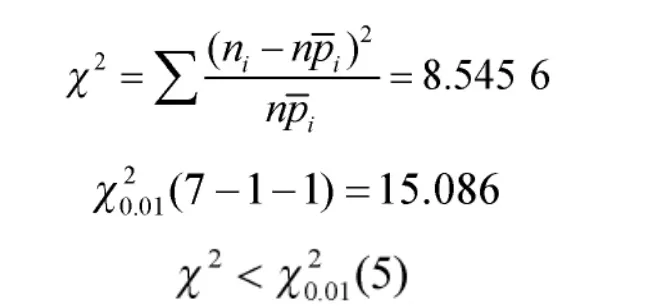
所以该型枪械故障分布服从指数分布。

以指数分布为模型，对表1 中的数据利用Matlab 软件进行建模，得到故障分布和指数模型拟合曲线对比，如图2 所示，其相关系数为0.993 93。

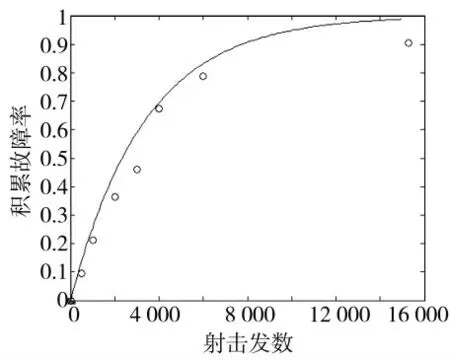
图2 某型枪械可靠性试验故障分布和指数模型拟合曲线图

由图2 可见，指数分布能比较近似地拟合该型枪械的可靠性特征。在可靠性理论中，指数分布是最基本、最常用的分布，适合于故障率（t）为常数的情况。从理论上来说，枪械在使用寿命内其故障可以修复，且修复后性能恢复，这就具有指数分布无记忆性的特点，所以可以利用指数分布的试验方案进行枪械可靠性试验。

2 枪械可靠性试验

指数分布的试验方案分为全数、定时、定数、序贯试验等［9，13］。本文研究枪械可靠性定时截尾和序贯截尾试验统计方案，试验统计方案中共有5 个参数［9］：

1）MTBF 假设值的上限值θ0，它是可以接收的MTBF 值。当受试品的MTBF 真值接近θ0时，指数分布标准型试验方案以高概率接收该产品。要求受试产品的可靠性预计值θp＞θ0才能进行试验；

2）MTBF 假设值的下限值θ1，它是不可接收的MTBF 值，当受试品的MTBF 真值接近θ1时，指数分布标准型试验方案以高概率拒收该产品；

3）鉴别比d，d=θ0/θ1，d 越小，则作出判断所需的试验时间越长，所获得的试验信息也越多；

4）生产方风险α，当产品的MTBF 真值等于θ0时被拒收的概率。即本来是合格的产品被判为不合格而拒收，致使生产方受损失；

5）使用方风险β，当产品的MTBF 真值等于θ1时被接收的概率。即本来是不合格的产品被判为合格而接收，致使使用方受损失。

枪械可靠性试验统计方案确定的实质是：已知上述参数，确定试验的样品数、试验时间（射弹量）和合格判据等试验要素。

2.1 定时截尾试验统计方案

2.1.1 使用方风险和生产方风险都有要求

假设生产方风险为α，使用方风险为β，MTBF假设值的上限值为θ0，MTBF 假设值的下限值为θ1。试验时，抽取n 支枪，射击到事先规定的时间t（即射弹发数），在［0，t］内出现r 次故障，若规定判定准则，且合格判定数为c，则：r≤c 时接收；r＞c 时拒收。

故障分布为指数分布的可靠性试验中，n 个产品在（0，t）内故障数服从（或近似服从）参数为nt/θ的泊松分布，其接收概率为：

式中，T=nt 为相应统计方案接收时所对应的总试验时间（台时）；θ 为MTBF 的假设值。

当已知α、β、θ0、θ1时，接收概率曲线应满足：

给c 一个初始值，通过式（8）迭代可以解得T=nt 和c，可以看出有多解，应根据实际试验要求作出选择，样品量n 与试验时间t，可以互相调剂，若样品量少，则试验时间（射弹发数）要增加。

确定定时试验方案时，预先知道试验持续的大概时间，使得试验规划人员可以在试验持续时间、使用方风险和生产方风险、检验上限和检验下限之间进行权衡，计算持续时间和接收故障数。

实例1 某型枪械在某种环境下要求θ1=1 000 发，θ0=3 000 发，d=3。若α=β=0.1，则应用式（8）迭代计算可选T=nt=9 300 发，c=5 这种试验方案，即试验射弹发数达到9 300 发时，故障数r≤5 时接收，r＞5 时拒收；若α=0.1，β=0.2，通过迭代计算可选T=nt=5 400发，c=3 这种试验方案，即试验射弹发数达到5 400发时，故障数r≤3 时接收，r＞3 时拒收。

2.1.2 只关注使用方风险

根据下述步骤推导试验统计方案：

可由式（9）计算得到拒收故障数r 所对应的总射弹发数T，即总试验射弹发数达到T 且累积的故障数小于r，则产品通过验证，否则不能通过验证。

2.2 序贯截尾试验统计方案

假定n 件产品进行寿命试验，总的试验时间为T，在此期间发生r 次故障，使用下述决策准则：

1）若T≥TA，接收并停止试验；

2）若T≤TR，拒收并停止试验；

3）若TR＜T＜TA，继续试验。

在继续进行的寿命试验中，若有r+1 次故障，再把实际总试验时间与TA、TR重新比较作出新的判断，如此类推，直到有接收或拒收结果为止。

已知α、β、θ0、θ1时有：

以T 和r 为坐标作图，可得接收区、拒收区和继续试验区。由于实际试验的现实要求，根据式（12）、式（13）限定试验截尾区域。

满足式（12）的r 的最小整数r0为试验中可以出现的最多故障数，而最长试验时间T0由式（13）计算。

实例3 某型枪械在某种环境下要求θ1=1 000 发，θ0=3 000 发，d=3，若α=β=0.1，应用式（10）～式（13）以试验时间和故障数为坐标作序贯截尾试验判决，如图3 所示。

图3 某型枪械可靠性序贯截尾试验判决图

图3 直观地表示了该序贯截尾试验的接收、拒收、和继续试验区。其判决方案如表2 所示。

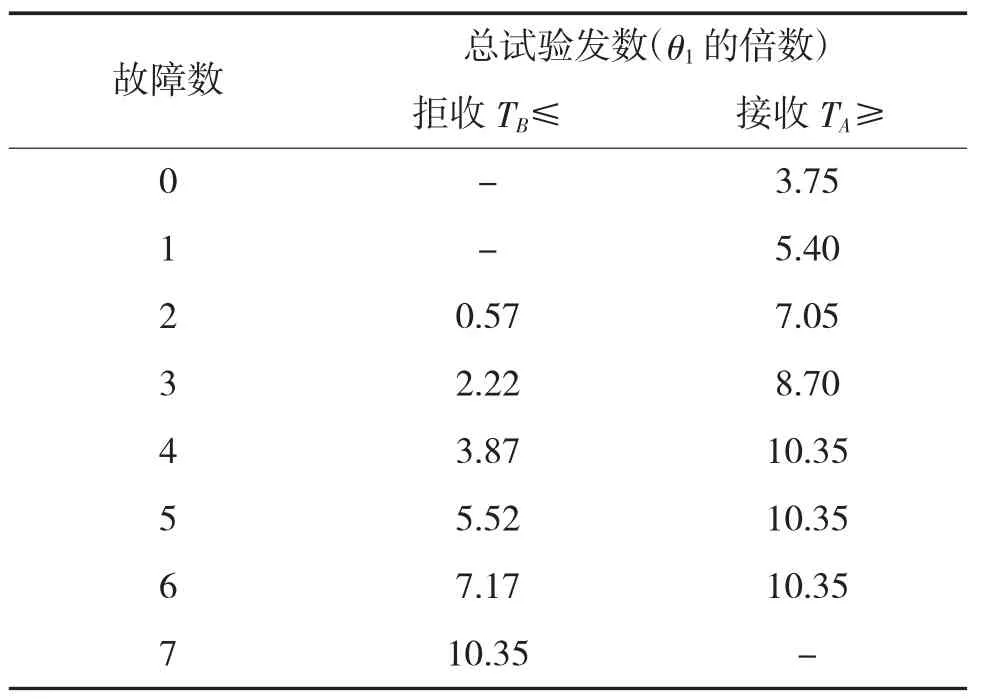
表2 某型枪械序贯截尾试验接收拒收判决表

实际试验时，如射弹发数超过3.75θ1=3 750 发，且没有出现故障，则接收这批产品，否则继续射击，继续按表中数值判决，直到得出判决结果为止。

序贯试验统计方案通常能较快地对MTBF 接近θ0和θ1的产品作出接收或拒收判决。对于MTBF 的真值较大或较小的产品，序贯试验所需的总试验时间可能差别较大［9］。该试验方案的缺点是：

1）不能确定试验发射弹数；

2）不能计算可靠性参数的观测值，鉴定试验不宜采用，一般用于验收试验。

3 可靠性参数的估计

可靠性试验不仅需要检验产品的平均故障间隔时间MTBF、故障率等可靠性参数是否达到规定的指标，还需要根据试验数据或现场数据对可靠性参数进行估计，如故障率的观测值（点估计值）和验证区间（L，U）等，从而有助于定量地把握产品的可靠性特征。故障率的参数估计需要规定验证区间（L，U）的置信度，建议采用置信度c=（1-2β）×100 %，如当使用方风险β=10 % 时，置信度c=80 %。在定时截尾试验中能进行产品可靠性参数的估计，方法如下。

3.1 接收时故障率的估计

当试验结果作出接收判决时，该试验停止前出现的责任故障数一定不大于接收判决故障数，试验必定是达到规定的试验时间而停止的。

1）故障率的观测值（点估计值）：

2）置信上下限系数为：

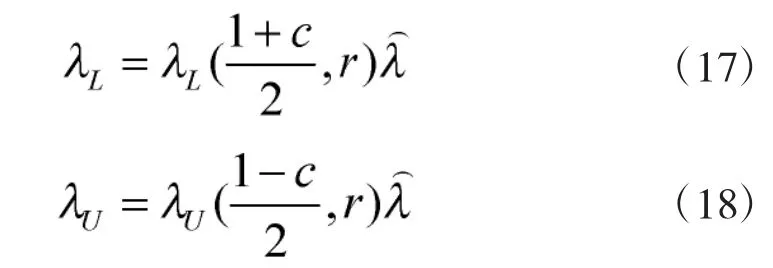
3.2 拒收时故障率λ 的估计

试验过程中若责任故障数达到拒收的判决故障数可立即停止试验，并作出拒收判决。拒收时故障率的估计与接收时的估计方法相同。

4 应用实例

假如某型枪械在某种环境下故障率指标要求不大于0.3%，在一次可靠性试验中，射击10 000 发弹，出现了12 次责任故障，可靠性评估如下：

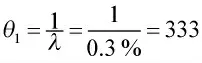
3）根据序贯截尾试验统计方案进行评估。该试验条件下，计算得接收拒收判决表如表3 所示：

表3 某型枪械序贯截尾试验接收拒收判决表

每一次责任故障出现时，将T 与TA、TR进行比较，由于T 均介于TA与TR之间，因此，作出继续试验的判决，当试验进行到射弹4 695 发时未出现新的责任故障，作出接收判决。可见在这次试验中序贯截尾试验统计方案较快地作出了判决。

可见，本文研究的试验统计方案和参数估计方法对枪械可靠性的评估结果具有一致性，试验统计方案和参数估计方法可行有效。

5 结论

1）各可靠性特征量之间存在换算关系，只要知道其中一个，则所有变量均可求得。本文对枪械常用可靠性特征量平均故障间隔时间和故障率进行了试验评估方法研究。

2）理论分析和试验经验说明可以利用指数分布的试验统计方案进行枪械可靠性试验。

3）可以应用定时截尾和序贯截尾试验统计方案进行枪械可靠性试验，定时截尾试验既可以用于判定可靠性是否合格，又可以对可靠性参数的真值进行估计，序贯截尾试验能较快地对MTBF 接近θ0和θ1的产品作出接收或拒收判决，不能计算可靠性参数的观测值。

4）实例应用说明本文研究的各可靠性试验统计方案对枪械可靠性的评估结果具有一致性，试验统计方案和参数评估方法可行有效，可以根据实际试验条件选择应用。