认知反思对初中生数学成绩的影响：基于三重加工心智模型

谢云天 史滋福 温辉冬

[摘 要] 选取2 844名初中生，通过认知反思测试（Cognitive Refletion Test，CRT）来探讨认知反思对初中生数学学业成绩的影响，并验证三重加工心智模型。结果发现：（1）认知反思与数学成绩显著正相关，而认知直觉与数学成绩显著负相关。（2）初中生在CRT三道题目中全部为正确反应的比例为51.51%，全部为直觉反应的比例为8.54%。（3）与认知直觉型学生相比，认知反思型学生的数学成绩显著更高。（4）认知直觉型显著负向预测数学成绩，认知反思型显著正向预测数学成绩。鉴于认知直觉、认知反思对数学成绩的影响，在培育学生算法心智的同时，还应促进反省心智的发展，培育数学理性思维。

[关键词] 认知反思;CRT;数学成绩;反省心智;三重加工心智模型

[中图分类号]G442    [文献标志码]A

一、问题提出

数学是一种多样化的、连续不断的、由问题驱动的人类创造性活动，是刻画客观世界和可能世界数量关系与空间形式的模式。[1]30为了学好数学这门结构严谨、逻辑严密的重要学科，也为了能取得理想的学业成绩，初中生在數学学习上投入了大量的时间。然而，在智力水平相当、学习环境一致的情况下，学生的数学学习表现仍然差异显著。[2]74不少人的数学学业成绩并不理想。许多学生因为数学学习困难或数学学习障碍而导致升学受阻、内心受创。因此，如何改进数学学习效果、提高数学学业成绩备受重视。

在影响个体数学成绩的诸多因素中，认知因素尤其是认知能力受到了广泛关注。个体在认知过程中常常表现出两种状态：一种是在没有意识思考的情况下快速执行的状态，另一种是比较慢且更具反思性的状态。[3]710在第二种状态中，需要消耗更多的认知资源，花费更多的时间。为了进一步考察这两种状态，Frederick（2005）[4]27编制了一个包括三道题目的认知反思测验（Cognitive Reflection Test，CRT）工具。它已成为评估直觉分析认知风格中的个体差异的工具，[5]341且被证明是个体在理性思维任务表现的有力预测因素。[6]149认知反思测验中，许多人倾向于给出自动的、肤浅的、引人注目的快速错误答案。正如Campitelli和Gerrans（2014）[7]434所证明的那样，CRT测试的是认知反思水平，而不仅仅是算术测试。它捕捉到了其他智力测试无法测量的理性思维的重要特征。[8]1275根据Sinayev和Peters（2015）[9]3的观点，在CRT中，为了给出正确的答案，个体需要经历两个步骤——第一步，抑制直觉冲动，进行认知反思;第二步，进行数学计算，发挥计算能力的作用。Gómez-Veiga，Vila Chaves，Duque和García Madruga（2018）[10]1以西班牙51名15.3岁至17.7岁的中学生为被试，应用了CRT等工具，结果发现，认知反思与数学成绩显著正相关，认知直觉与数学成绩显著负相关。

研究者认为，个体在CRT上的反应反映了由双过程理论（Dual Process Theory）定义的两个相互竞争的心理过程之间的相互作用。[11]86然而，双过程理论忽视了发起压制功能的高级认知功能，而这种功能正是反省心智的属性。为此，加拿大多伦多大学应用心理学和人类发展学系荣誉教授、2010年格文美尔大奖获得者基思·斯坦诺维奇（Keith E. Stanovich）提出了三重加工心智模型（Tripartite Model of Mind）。他认为，人类同时具备自主心智（autonomous mind）、算法心智（algorithmic mind）以及反省心智（reflective mind）。这三种心智构成了三重加工心智模型的主体。如果说自主心智对应双过程理论的过程一，那么算法心智和反省心智对应的是过程二。反省心智是三重加工心智模型重点突出的心智。发起对自主心智产生的劣质反应的压制和对产生优化反应的模拟仿真是这种心智必须具备的两个特点。[12]49而且，理性思维的个体差异既可以源自算法心智，也可以源自反省心智。所以，在重视算法心智的同时也应重视反省心智。

根据斯坦诺维奇的观点，认知反思正是反省心智的主要表现之一，是获得理性思维的重要条件。而数学理性思维是数学核心素养的灵魂，只有在数学理性思维的指引下，数学核心素养才会产生价值和意义。[13]79此外，数学解题是数学学习中的重要认知活动，而数学解题反思既是数学解题过程中内在的一个重要组成部分，[14]11也是对数学解题活动更进一步的分析与思考。[15]95这种反思属于认知反思，当然也是反省心智的体现。连四清和郭海杰（2005）[16]57在针对中学数学学困生题后反思的干预中，引导学生围绕“你是怎样发现和解决问题思路的”“你运用了哪些基本的数学思想方法”“解题时你走过那些弯路”“解题时容易犯什么样的错误”等问题进行反思，取得了较为理想的成效。

从已有研究来看，虽然国内外探讨反思与数学尤其是数学解题关系的研究有不少，但缺乏从理性思维的角度深入揭示认知反思对数学成绩的影响，理性思维如何影响数学成绩不甚明了，而CRT可以测量反映理性思维特征的认知反思，基于此，本研究以CRT为测量工具，探讨认知反思对数学成绩的影响，以期为提升初中生认知反思水平和数学成绩、改进数学教育教学提供科学依据和借鉴。

二、研究方法

（一）对象

选取江西省三所公立中学的2 844名初中生。其中，男生1 551人（54.54%），女生1 293人（45.46%）。初一947人（33.30%），初二979人（34.42%），初三918人（32.28%）。被试的年龄范围为11岁至17岁（Mage=13.58，SD=1.01）。

（二）工具

1.认知反思测试题

认知反思测试（Cognitive Refletion Test，CRT）由Frederick（2005）编制，用于评估一个人在面对基于文本的数学问题时的倾向和反思能力。CRT一共包括3道题目：

第1题：球和球拍合计1.1元。球拍比球贵1元。请问球是多少钱？

第2题：5台机器生产5件工具需要5分钟。请问100台机器生产100件工具需要多长时间？

第3題：湖水上有一片睡莲叶子。睡莲叶子每天变大一倍，48天能把整个湖水铺满。请问多少天后睡莲能够铺满湖水的一半？

根据Pennycook等（2016）的观点，本研究将学生在CRT中的表现划分为三种认知类型，即三道题目都答对的认知类型命名为“反思型”，三道题目都为直觉回答的认知类型命名为“直觉型”，其他表现命名为“其他型”。

2.数学学业成绩

来自最近一次期中考试的数学成绩。将数学成绩在各自学校的相应年级内标准化，转化为标准分。

（三）程序

以班级为单位，利用班级学生集中上课时间发放问卷。在问卷作答过程中，要求学生认真、如实填写每一道题目，并当场回收。问卷回收后，应用SPSS25.0，R软件对数据进行分析和绘图。

三、结果

（一）主要变量的相关矩阵

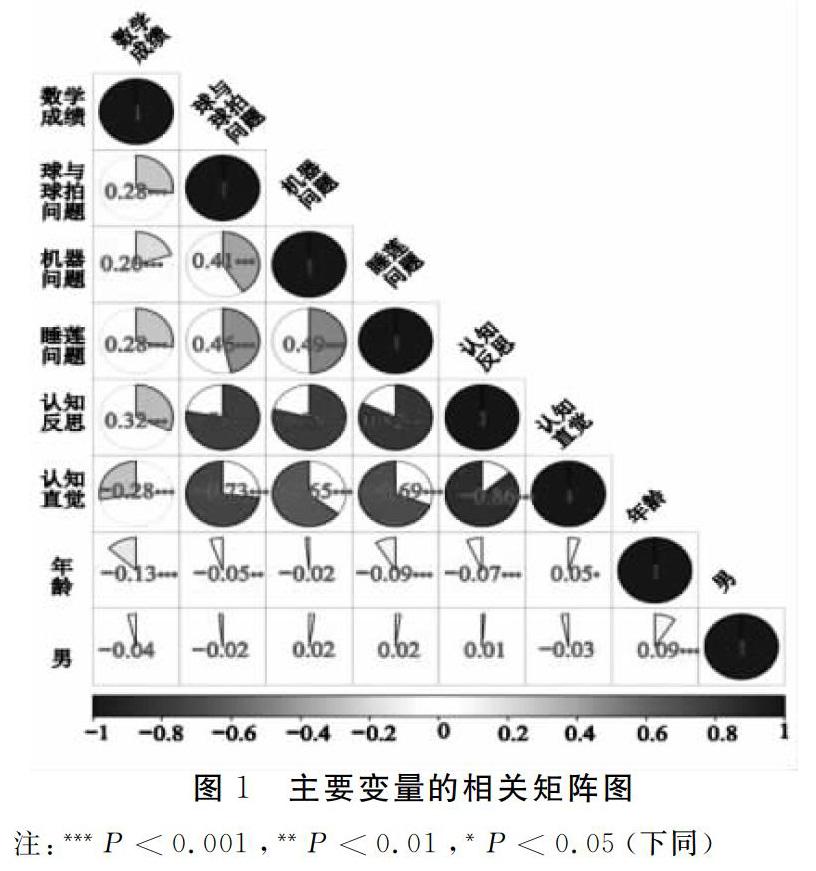
相关分析的结果显示（见图1），初中生在CRT三道题目的得分与数学成绩均为显著正相关（P<0.001），认知反思与数学成绩显著正相关（P<0.001），认知直觉与认知反思、数学成绩显著负相关（P<0.001）。此外，年龄与认知反思显著负相关（P<0.001），与认知直觉显著正相关（P<0.05）。

（二）初中生在CRT中的测试结果分析

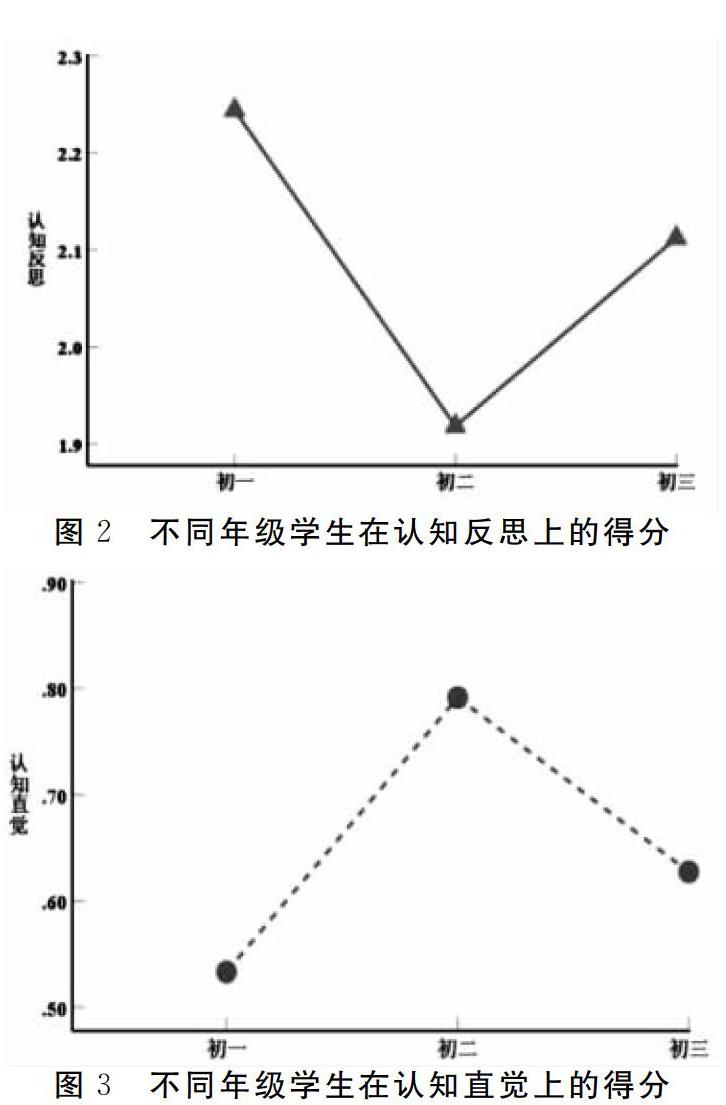
如表1所示，在CRT中的三道题目中，按照正确反应比例由高到低的顺序排列，依次是机器问题、球与球拍问题以及睡莲问题;按照直觉反应比例由高到低的顺序排列，依次是球与球拍问题、睡莲问题以及机器问题。三道题目均为正确反应的比例仅为51.51%。有8.54%的学生在三道题目上都表现出直觉反应。因为年龄与认知反思、认知直觉均为显著相关，因此本研究还考察了不同年级学生在CRT中的表现。结果显示，在认知反思得分上，初一显著高于初二、初三，初三显著高于初二;在认知直觉得分上，初二显著高于初一、初三。见图2、图3。

（三）不同认知类型、性别学生的数学成绩

以认知类型、性别为自变量，年龄为控制变量，数学成绩为因变量，进行多因素方差分析。结果显示，认知类型的主效应显著（F=125.62，P<0.001，ηP2=0.081），性别的主效应不显著（F=2.44，P=0.12，ηP2=0.001），认知类型与性别的交互效应不显著（F=0.43，P=0.65，ηP2=0.001）。

多重比较结果显示，反思型学生的平均数学成绩（0.270.99）最高，其他型（-0.230.94）次之，直觉性最低（-0.550.81），P<0.001。而且，反思型学生的数学成绩在1分左右的范围内相对集中，直觉型在-1分左右的范围内相对集中，其他型相对平均一些（见图4）。在三种认知类型中，男生的数学成绩均低于女生（见图5）。而且，数学成绩的性别差异检验结果也显示，男生数学成绩（-0.031.03）低于女生数学成绩（0.040.96），P=0.06，Bootstrap95%CI[-0.14，-0.01]。

（四）主要变量对数学成绩的预测

首先，把年龄、性别（1=男，0=女）作为控制变量，以直觉反应为因变量，数学成绩为自变量，建立模型1，结果显示，直觉反应显著负向预测数学成绩，β=-0.27，Bootstrap95%CI[-0.31，

-0.25];该模型的调整后R2=0.092，F=97.25，P<0.001。然后，把年龄、性别（1=男，0=女）作为控制变量，以“反思型”“直觉型”（以“其他型”为参照）为因变量，数学成绩为自变量，建立模型2，结果显示，反思型显著正向预测数学成绩，β=0.24，Bootstrap95%CI[0.41， 0.56];直觉型显著负向预测数学成绩，β=-0.09，Bootstrap95%CI[-0.43，-0.21];该模型的调整后R2=0.097，F=77.20，P<0.001。

四、讨论

人类是认知吝啬鬼，一般表现为默认低计算成本的处理机制。[17]423本研究对初中生的认知反思测试结果也验证了这个观点。CRT三道题目为直觉反应的比例均达两成左右，三道题目全为反思反应的比例仅过半数。不过，在本研究中初中生的CRT表现好于Gómez-Veiga等（2018）的研究发现。这可能是因为中国学生的数学素养相对更好。2019年12月公布的2018年国际学生评估项目测试结果显示，中国学生在数学测试中排名世界第一。然而，一个必须引起重视的发现是，随着年龄的增长，初中生的认知反思表现呈下降趋势，而认知直觉表现则呈上升趋势。年级差异的比较结果显示，初二学生的认知反思表现最差，最容易用直觉进行反应。这可能因为初二年级是学生心理发展的特殊时期。处于青春期的他们逆反心理突出，容易表现出种种心理上的矛盾，[18]217在认知活动中更不愿意花费时间和精力，不愿意停下来思考，因而更容易出现直觉的、错误的反应。为此，应重点针对初二学生进行认知反思训练，可以以“认知自我”“调节情绪”“反思与直觉”等内容为主题开展活动，促进他们认知反思水平的提升。

本研究还发现，认知反思与数学成绩显著正相关，认知直觉与数学成绩显著负相关。这和Gómez-Veiga等（2018）的研究发现是一致的。而且，本研究的结果显示，反思性学生的数学成绩显著最高，直觉型学生的数学成绩显著最低。反思型正向预测数学成绩，而直觉型负向预测数学成绩。这个结果验证了三重加工心智模型，证明了反省心智的重要作用。对于数学学习，最核心的问题是解题，学生成绩差的最为突出的问题是不会仔细审题和解题后不做反思。[19]90反思可以加深对问题的理解，并促进学习。反思的人能更好地控制自己的思维，并能决定走哪条路，而不仅仅是参与行动。[20]535当然，由自主心智发出的直觉反应并不一定有害。实际上，在人类的进化过程中，它起到了很大的作用。可问题是，直觉反应或吝啬加工的收益和成本取决于环境的性质。[17]423当环境不良时，个体需要通过反省心智压制劣质反应。为此，数学教育工作者应该深入研究如何引导学生识别和应对不同情境下的数学问题，避免陷入非理性的泥潭。

值得一提的是，在本研究中，虽然认知类型和性别的交互效应不显著，性别的主效应也不显著，且在本研究的回归分析中男性的预测作用也是不显著的，但数学成绩的性别差异检驗结果显示，Bootstrap的置信区间不包括0，男生的数学成绩低于女生。这说明数学成绩的性别差异受到多方面因素的影响。而且，这种差异远比通常人们所认为的复杂的多。[21]1986还需要未来进一步探讨。

综上，本研究通过应用CRT测量工具探讨了认知反思对初中生数学成绩的影响，揭示了认知直觉、认知反思两种认知风格的不同影响，并突显了反省心智在数学学习中的重要地位，验证了三重加工心智模型。与此同时，本研究也存在一些不足。其一，本研究采用问卷进行调查，收集资料的方法不够全面。未来的研究可以在问卷调查的基础上结合焦点访谈，深入挖掘认知直觉型学生和认知反思型学生的质性资料。其二，初中生处于身心发展、变化的重要阶段。从认知直觉到认知反思，或者从认知反思到认知直觉，二者之间存在一个怎样的内部变化过程？初二学生的认知反思水平为什么会显著区别于其他两个年级？未来的研究可以选取典型个案，开展纵向研究，进一步揭示青少年的认知风格。

五、结论

与认知直觉型学生相比，认知反思型学生的数学成绩更高。在初中的三个年级中，初二学生的认知反思表现最为糟糕，最容易进行认知直觉反应。鉴于认知直觉和认知反思对数学成绩的影响，在培育初中生算法心智的同时，还应促进其反省心智的发展，培育初中生的数学理性思维。

[参考文献]

[1]唐恒钧，徐元根，张维忠.基于问题链的中学数学有效教学研究——一项课例研究的启示[J].数学教育学报，2018（3）：30-34+44.

[2]王光明，佘文娟，宋金锦.基于NVivo10质性分析的高效数学学习心理结构模型[J].心理与行为研究，2014（1）：74-79.

[3]Epstein S.Integration of the cognitive and the psychodynamic unconscious[J].American Psychologist，1994（8）：709-724.

[4]Frederick S.Cognitive reflection and decision making[J].Journal of Economic Perspectives，2005（4）：25-42.

[5]Pennycook G，Cheyne JA，Koehler，DJ，et al.Is the cognitive reflection test a measure of both reflection and intuition？[J].Behavior Research Methods，2016（1）：341-348.

[6]Toplak ME，West RF，Stanovich KE.Assessing miserly information processing：An expansion of the Cognitive Reflection Test[J].Thinking and Reasoning，2014（2）：147-168.

[7]Campitelli G，Gerrans P.Does the cognitive reflection test measure cognitive reflection？A mathematical modeling approach[J].Memory and Cognition，2014（3）：434-447.

[8]Toplak ME，West RF，Stanovich KE.The Cognitive Reflection Test as a predictor of performance on heuristics and biases tasks[J].Memory and Cognition，2011（7）：1275-1289.

[9]Sinayev A，Peters E.Cognitive reflection vs.calculation in decision making[J].Frontiers in Psychology，2015（6）：1-16.

[10]Gómez-Veiga，I.，Vila Chaves，J.O.，Duque，G.，& García Madruga，J.A.A new look to a classic issue：Reasoning and academic achievement at secondary school[J].Frontiers in Psychology，2018（9）：1-12.

[11]Cheng J，Janssen C.The relationship between an alternative form of Cognitive Reflection Test and intertemporal choice[J].Studia Psychologica，2019（2）：86-98.

[12]斯坦诺维奇.超越智商：为什么聪明人也会做蠢事[M].张斌，译.北京：机械工业出版社，2015.

[13]朱立明.基于深化课程改革的数学核心素养体系构建[J].中国教育学刊，2016（5）：76-80.

[14]徐彦辉.数学解题后的“回顾与反思”与数学问题的提出[J].数学教育学报，2015（1）：9-12.

[15]马文杰，徐莉芳.“数学解题反思”研究的元研究[J].数学教育学报，2018（5）：93-98.

[16]连四清，郭海杰.中学数学学困生题后反思的元认知技能培训[J].数学教育学报，2005（2）：56-58.

[17]Stanovich KE.Miserliness in human cognition：the interaction of detection， override and mindware[J].Thinking and Reasoning，2018（4）：423-444.

[18]林欽寿，林娇容.初二学生心理健康状况的调查[J].宁德师专学报：自然科学版，2008（2）：216-218.

[19]张晓拔.数学教学要重视培养学生的反思习惯[J].数学教育学报，2008（6）：90-92.

[20]Wheatley GH.The role of reflection in mathematics learning[J].Educational Studies in Mathematics，1992（5）：529-541.

[21]刘蕴坤，陶沙.数学成就的性别差异[J].心理科学进展，2012（12）：1980-1990.

[22]徐丽丽，王威威，于立娜.初中生学习压力、人格对学习倦怠的影响[J].牡丹江师范学院学报：哲学社会科学版，2015（6）：130-132.

[23]卿再花，吴彩虹，曹建平.认知行为团体辅导对大学生手机成瘾干预效果研究[J].牡丹江师范学院学报：社会科学版，2019（2）：126-131.

[责任编辑]王立国

Abstract：A total of 2 844 junior high school students were selected to explore the influence of cognitive reflection on mathematical achievement through CRT，and to verify Tripartite Model of Mind.Results were as follows：（1）Cognitive reflection was significantly positively correlated with mathematical achievement，while cognitive intuition was significantly negatively correlated with mathematical achievement.（2）In the three CRT questions，the proportion of all correct responses was 51.51%，and the proportion of all intuitive responses was 8.54%.（3）Compared with students of cognitive intuition，students of cognitive reflection have significantly higher mathematical achievement.（4）Cognitive intuition significantly predicted mathematical achievement negatively，while cognitive reflection significantly predicted mathematical achievement positively.In view of the influence of cognitive intuition and cognitive reflection on mathematical achievement，it is necessary to promote the development of reflective mind and cultivate mathematical rational thinking while cultivating students' algorithmic mind.

Keywords：cognitive reflection;CRT;mathematical achievement;reflective mind;Tripartite Model of Mind