考虑H2O影响的绝缘子电晕放电数值仿真

曾晗，张靖，程宏波，辛建波，王利娜

(1.国网江西省电力有限公司电力科学研究院，江西 南昌 330096；2.华东交通大学 电气与自动化工程学院，江西 南昌 330013)

随着电网和电气化铁路的不断扩大，人们对高电压绝缘子的研究进一步深入，其中绝缘子表面的电晕放电是一个重要的研究方面。高压线路中绝缘子表面发生电晕放电，会引起电能的巨大损耗、通信以及噪声干扰，放电过程中会逐渐破坏绝缘子的绝缘性能。电晕放电是气体放电的一种，多年来研究者对气体放电做了深入的研究和分析。KOSSYI I A 等提出了氮-氧混合物中非平衡放电的动力学方案，包括电子态激发、重粒子的电子碰撞和电离、电子附着和分离、电子-离子和离子-离子重组、中性粒子的化学转化和离子转换[1]。SUN B等利用脉冲流光电晕放电形成多种活性物质[2]。2013年 KOMURO A在利用二维数值模拟方法研究常压流光放电中OH自由基的行为时，考虑了H2O分子参与的流光放电[3]，但是其主要研究的是常压流光放电中OH自由基形成的机理。国内研究电晕放电在20世纪末陆续的出现，现在相关研究也不断地深入。2014重庆大学提出了一种改进的电晕放电混合模型，研究了负电晕放电过程中重粒子的特性[4]。2016年刘民等[5]搭建局部放电测试系统，研究了干燥空气中直流电压下电晕放电发展过程。2018年张友鹏、刘家治等人结合实际工程，研究了大气压下接触网绝缘子电晕放电特性，分析了相应的电子密度、电子温度和电场强度的分布，同时分析了电晕放电在空气中的放电过程[6]。从国内外研究现状分析，电晕放电最深入的研究就是考虑了空气中N2和O2的相关粒子反应，但是没有考虑潮湿环境中相关的H2O分子反应。通过大量相关的文献发现，到目前为止气体放电的研究主要分为：①是通过在真空环境中加入一种或几种气体，然后分析气体放电过程；②是通过大气压下O2和N2混合，研究相关的气体放电过程。以上2种方法几乎没有考虑水分子的影响，而在潮湿环境下，水分子的影响是不可避免的。

本文依照气体放电的相关机理，并结合等离子体模型和流体力学模型，在相应的电晕放电反应中添加H2O的相关反应方程；同时基于COMSOL有限元仿真软件中的等离子体模块，采用了流体力学中的扩散方程对潮湿环境下绝缘子表面的电晕放电进行二维数值仿真。为了更好地研究绝缘子表面的电晕放电，本文结合KOMURO A在流光放电中的水反应和张友鹏绝缘子电晕放电的研究，考虑了潮湿空气中的主要成分N2、O2和H2O的激发、电离、碰撞和化学反应等离子反应。研究放电过程中电场强度、电子数密度、电子温度和相关离子数密度随时间的分布，并且与干燥环境下的电晕放电相对比，分析水分子对放电的影响，以及水反应产生相应物质在绝缘子表面的分布状况。

1 潮湿环境下电晕放电模型

1.1 流体动力学模型

传统流体动力学模型主要由电子连续性方程、重粒子多组分扩散输运方程、重粒子动量方程、能量平衡方程和Poisson方程组成。空气放电物理过程的分析在数值分析中实质是求解偏微分方程问题[7]。为了准确、细致地重现电晕放电的微观物理过程，本文加入等离子体碰撞反应和化学反应模型，其电子的连续控制方程为[8]：

(1)

(2)

式中：ne、ni和nn分别为电子、正离子和负离子数密度；E为电场强度；Re为化学反应产生电子的净速率；we为电子的漂移速率；α为电离系数；η为附着系数；Rei为电子与离子的复合系数；vdet为解离系数；S0为初始电子的出现速率；Sph为光电离项，大气压下空气放电过程中电子与中性粒子之间的碰撞光电离过程剧烈，即使如此，光电离产生的电子数还是远小于碰撞电离产生的电子数，故本文光电离项忽略不计；t为时间；μe为电子迁移率;De为电子扩散性能函数。

平均电子能量Te(又称为“电子温度”)的平衡方程[9]为

(3)

式中：Γe为电子密度通量；χ=(5/2)neDe为热散射系数；ST为描述电子热源和冷源函数。解式(3)可以近似地考虑电子热传导引起的非局域效应。

为了准确地描述潮湿环境下电晕放电的放电区域，引入了电子能量Te的守恒方程，即Farouk的改进模型[10]

(4)

式中：nk为第k种物质的密度；ηk为电子与k物质碰撞后能量损失的速率系数；me为电子质量；Mk为第k种物质的质量；T为气体温度；ve,n为电子动量转移碰撞频率；je为能量增益系数；kB为玻尔兹曼常数。

其中电子密度方程为：

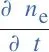
(5)

Γe=-(μe·E)ne-(Dene).

(6)

式中u为中性流体速度矢量。

平均电子能量

(7)

电子温度定义为

(8)

电场通过泊松方程来计算得

(9)

式(7)—(9)中：nε为电子能量密度；ε0为自由空间的介电常数；εr为相对介电常数；e为电子电荷；V为电势。

电场强度E的表达式为

E=-V.

(10)

1.2 等离子模型

设等离子模型温度为293.1 K(20 ℃)，压强为1个标准大气压，考虑到电晕放电的速度一般为十几纳秒，绝缘子上的电压变化相对于电晕放电电压的变化较为缓慢，可以近似地看作为是直流放电。设上端阳极电压为39 kV[11]，阴极接地，电势为0，并设置了1 pF的阻断电容与5 000 Ω的保护电阻[6]。

等离子模型选用的是电气化铁路用绝缘子中的FQB-25/8复合绝缘子。本文选择的绝缘子实际尺寸包括了8个小伞裙和9个大伞裙，结构如图1所示(单位mm)，但考虑到计算模型的复杂性和重复性，模型选择首尾金具及2个大伞裙和1个小伞裙，简化绝缘子的模型如图2(b)。这样既能研究电晕放电对绝缘子的影响，又不会耗费太多的计算时间。绝缘子模型在进行仿真计算中的重要一步就是网格剖分，网格剖分会影响计算的复杂性和准确性。本文研究重点是电晕放电对绝缘子表面的影响，而金属的曲率半径也会对电晕放电造成影响，故划分网格时对绝缘子表面和金具的凸出处都进行细化，而其他部分只做常规处理，剖分图如图2(a)。

图1 FQB-25/8复合绝缘子Fig.1 FQB-25/8 composite insulator

图2 绝缘子几何模型和网格剖分Fig.2 Geometric model of insulator and mesh generation

1.3 边界条件

绝缘子表面电晕放电过程中，入射离子和电子通量引起的电荷会在表面积累，故相应的边界方程[12]为

(11)

式中：D1和D2分别为界面两侧电通量的法向分量；Ji为壁上总离子电流密度的法向分量；Je为壁上总电子电流密度的法向分量。

1.4 二次发射系数条件

电子打在绝缘子表面会产生二次电子，二次电子在表面正电荷的吸引下会重新打在绝缘子表面上。故绝缘子的仿真计算中添加了相应的仿真条件。模型中阴极和阳极的电子通量为[13]：

(12)

(13)

式中：Γi为离子密度通量；vth,e为电子热速度；为二次电子发射系数；qi为第i个离子的带电量。

BURKE E A对不同聚合物材料的实验数据进行了总结归纳，得出了二次电子发射系数随入射电子能量变化的经验公式，发现材料发射系数K是与聚合物的发射效率成正比的，与聚合物组成的复杂程度直接相关[14]，结构越复杂K值越小，发射电子的效率也就越低，从而有利于抑制电子崩的形成。故本文考虑设置的二次发射系数K较小，阴极设为0.1，阳极设为0，伞裙设为0.05。

1.5 等离子区的放电反应

模型计算以潮湿的空气作为反应气体，即在N2和O2体积比为4∶1的干燥空气中加入10%的H2O(50 ℃左右空气中的饱和水汽含量)。粒子间的反应常见的是碰撞反应(包括弹性碰撞、激发和电离)，粒子之间还会发生二体重组、三体重组、解离重组、电子附着、电子逸出、电荷转移和离子转换、分子离子转换、去激发等；但是考虑到绝缘子模型计算的复杂性，本文主要采用6类粒子间反应。其中电子碰撞横截面积的数据来自于等离子数据交换中心[15]。

6类粒子间反应为：

a)碰撞反应(弹性碰撞、电离、激发)。

R1：e+N2→e+N2，m/M=1.95010-5;

R2：e+O2→e+O2，m/M=1.70010-5;

R3：e+H2O→e+H2O，m/M=3.04310-5;

R6：e+H2O→2e+H2O+，Δε=13.00 V;

R7：e+H2O→e+H2O，Δε=0.20 V;

R8：e+H2O→e+H2O，Δε=0.41 V;

R9：e+H2O→e+H2O，Δε=0.43 V;

R10：e+H2O→e+H+OH，Δε=7.00 V;

R11：e+H2O→e+O+H2，Δε=13.00 V。

b)电子与离子的重组。

R16：H2O++e→OH+H，k=3.8010-13;

R17：H2O++e→H2+O，k=1.4010-13;

R18：H2O++e→H+H+O，k=1.7310-13。

c)离子间的重组。

R21：H2O++O-→H2O+O，k=4.0010-13;

d)电子附着反应。

R24：e+H2O→H2+O-，横截面积;

R25：e+H2O→OH+H-，横截面积;

R26：e+H2O→H+OH-，横截面积。

e)电子的脱离(逸出)。

R28：H-+H→H2+e，k=2.0010-15;

R29：H-+O2→HO2+e，k=1.2010-15;

R30：OH-+H→H2O+e，k=1.4010-15;

R31：OH-+O→HO2+e，k=2.0010-15。

f)电荷的转移和离子转换。

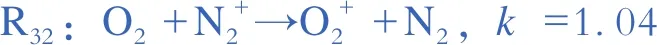
R42：H-+H2O→OH-+H2，k=3.8010-15。

其中：R1—R42为离子反应式；温度的比值Tr=T/Te，T为气体的温度(K)；m/M为电子质量比；Δε为阈值电压(能量损耗);R33—R40中M代表O2和N2；k为反应速率(二体反应为m3/s，三体为m6/s)。二体反应指有2个粒子参与的反应如R18、R32等，三体反应指有3个粒子参与的反应如R23、R33等。

表1 表面反应Tab.1 Surface reactions

2 结果与分析

2.1 电势与电场的发展规律

图3(a)左图为放电区域的几何模型，其中上端阳极是绝缘子直接接触高压的一端，下端阴极是接地极。图3(a)右图为电场等值线分布，它满足电场强度E的表达式(10)，即在电势密集的位置电场强度值较大，而在稀疏的位置电场强度值较小；并且电场集中的区域开始逐渐离开阳极和阴极区，幅值也不断地减小。这是由于在阳阴两极附近发生强烈粒子碰撞和化学反应，产生大量电子、正离子、负离子，其中速度迁移较快的电子会增强金具与等离子区域之间的电场强度[17]。

图3(b)为电势与电场强度发展曲线。从图3(b)可以看出：在放电起始(t=5 ns)，绝缘子表面电势和电场强度值都比较小，电势呈现梯形分布，而电场在绝缘子金具两端附近发生了畸变；随着时间的增加及放电的不断发展，电势逐渐增大，而在绝缘子阳极和阴极附近的电场畸变也越来越大。

图3 电势与电场强度的分布图Fig.3 Distribution diagram of electric potential and electric field

2.2 空间电荷密度的发展规律

图4为绝缘子沿面的不同时间点的电子密度曲线图。从图4可以明显地发现伞裙与阳极的电子密度随着时间的增加，在t=25 ns后电子密度急剧增加。阳极电子密度的增加是因为随着初级电子雪崩向阳极堆积，同时在阳极附近发生激发与电离；在较大电场力的作用下，电子迅速迁移，与附近离子更激烈地发生碰撞、电离，使得电子密度迅速增高。阴极附近的电子密度从放电开始，一直维持比较低的密度，这是因为尽管阴极附近电场强度很大，电离了大量的电子和离子，但是电子的迁移速率很快，在阴极几乎没有停留，绝缘子阴极沿面的离子不能持续地与电子发生碰撞电离。其中在伞裙的空间电子密度与如图5所示的干燥环境下的相比，电子密度要低上几个数量级，其原因是环境湿度越高，空气中的水分子增多，电子与水分子碰撞几率增大，碰撞后形成活动能力很差的负离子，碰撞能量及电子崩的作用减弱使伞裙的电子密度远低于干燥环境下的电子密度。

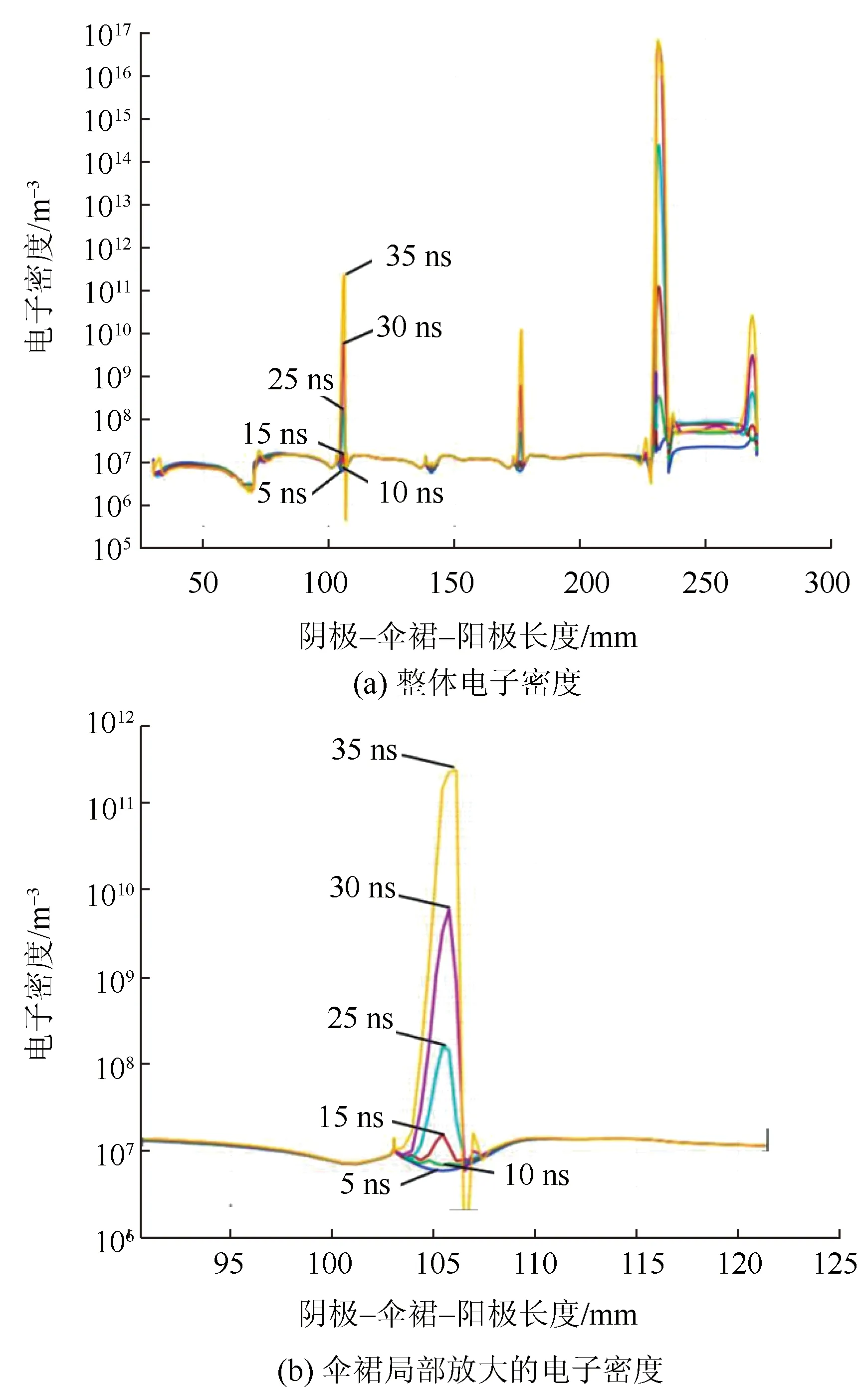
图4 绝缘子沿面的电子密度Fig.4 Electron density along the surface of insulator

图 6为阳极表面不同阶段电子密度变化。从图6(a)可以看出：在放电的初期电子密度发展是比较均匀地附着在阳极端[18]，这是因为在外电场的作用下，电子主要是以漂移为主。从图6(b)发现：随着时间的增大，电子密度在阳极出现指数级增大，并且开始缓慢地远离阳极，这是因为电子密度的增大让这片区域的电场强度出现了不同的梯度，使得电子运动不仅受到外电场作用，同时电子会发生扩散运动，从电子浓度高的点向浓度低的点运动。

图5 干燥环境下绝缘子沿面的电子密度Fig.5 Electron density along the surface of insulator in dry environment

图6 阳极表面不同阶段电子密度变化Fig.6 Electron density variation of anode surface at different stages

2.3 电子温度发展规律

电晕放电时电子温度的变化反映了碰撞电离反应和能量转移速度的变化，即粒子反应的剧烈程度。图7为电子温度变化曲线，由图7发现：在大伞裙的边沿以及绝缘子附近的电离区域的电子温度呈速率较大的正增长，且出现了极大值，而中间小伞裙的电子温度增加较慢；伞裙与绝缘子附近迁移区的电子温度都是迅速地下降，而在其他等离子放电区的电子温度是保持在一个稳定的数值。前者的变化图与电场曲线变化非常相似，从而证明通过电场的焦耳热效应所产生的能量可以使电子温度升高[19]，由图3(b)和图7对照，它们之间是正相关的；后者也与电场强度紧密相关，由于小伞裙的电场不够大，放电开始时电子不能持续与其他粒子发生碰撞电离，故电子温度增加缓慢。

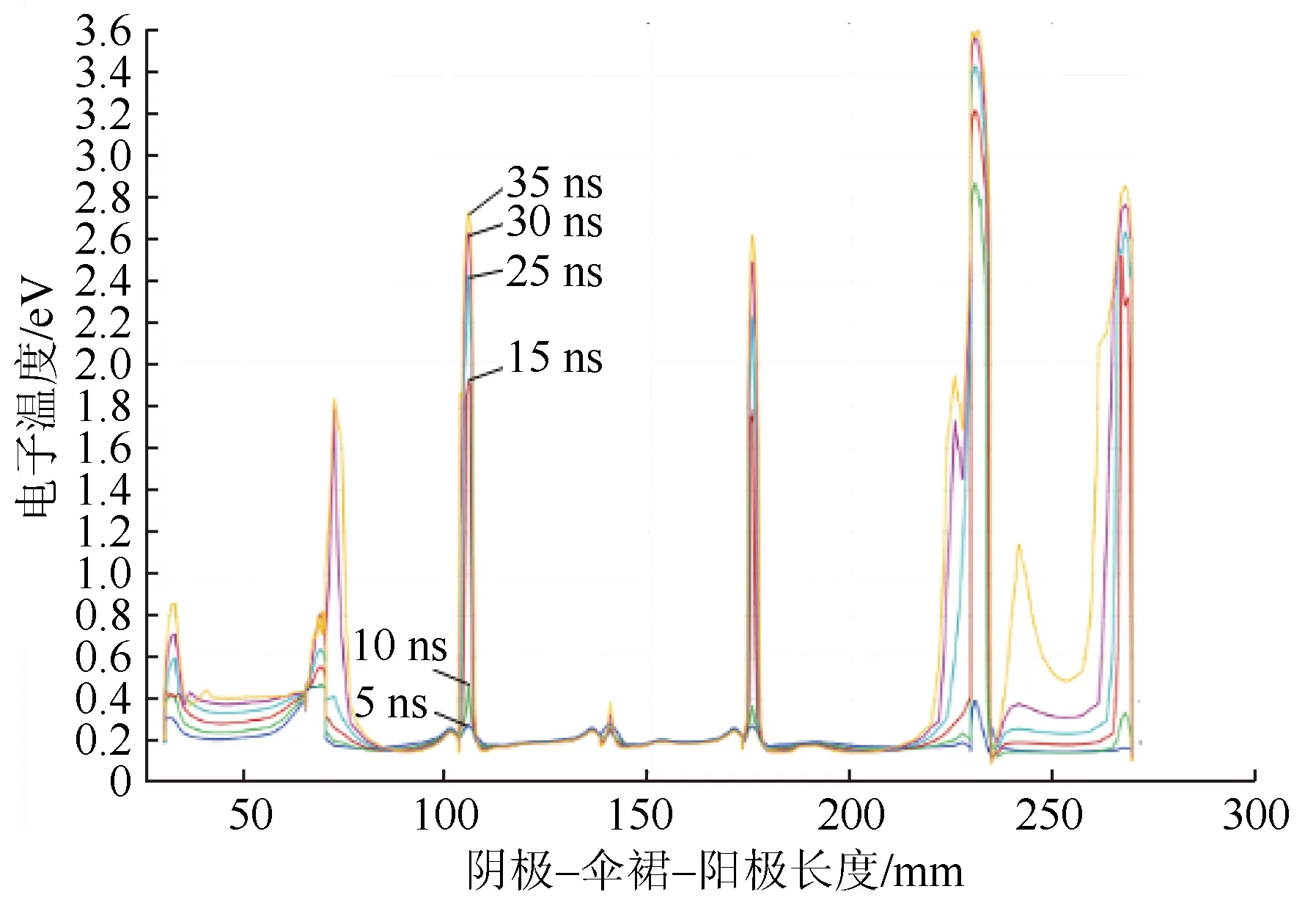
图7 不同时刻电子温度变化曲线图Fig.7 Curve of electron temperature change at different moments

2.4 潮湿环境与干燥环境电晕放电比较

潮湿环境下绝缘子附近的水分子是必然存在的，并且与干燥环境相比水分子的含量较多。在电流通过后,绝缘子的金具与导线的连接处会发热蒸发分解绝缘子附近的水滴，绝缘子附近放电空间水分子数目增多。2种环境下电晕放电比较见表2。从表2可知，潮湿环境下的电子温度与干燥环境下(不考虑水分子)相比，干燥环境下电晕放电中电离区的电子温度最大值在6 eV左右，而潮湿环境下电离区最大值在8 eV左右。电子温度的升高是因为电离系数随相对湿度的增加造成的，电子与空气中水分子发生碰撞电离次数的增加，使电离区等离子反应增强，电子温度升高[20-22]。

图8为2种环境下的粒子密度对比分析图。由图8看出本文所做的干燥环境下电晕放电的仿真与文献中的数据基本吻合。结合图9和表2发现：在t=30 ns时，潮湿环境下电晕放电的电子与离子密度要低于干燥环境下的；但是在t=35 ns时可以明显地看出潮湿环境下电晕放电的电子与离子密度要大于干燥环境下的。这是因为在水分子的参与下，电子与水分子的碰撞电离的电压阈值部分低于干燥环境下的，而反应速率部分高于干燥环境下的，在同等电场和电势下抑制了N2与O2相关粒子的产生；但是随着时间的增大及电子雪崩发生，空间中粒子反应加剧，电子与粒子密度增大。

表2 2种环境下电晕放电比较Tab.2 Comparison of corona discharge in two environments

图8 2种环境下的粒子密度的对比分析Fig.8 Ion density comparison in two environments

图9 t=30 ns时电子密度对比分析分布Fig.9 Electron density comparative analysis distribution diagram as t=30 ns

2.5 潮湿环境下重要粒子分析

本文主要分析在潮湿环境下的电晕放电，而H-、OH-和H2O+就是其中与水有关的离子成分。图10为这3种离子在阳极附近的曲线图，本文对其作了平滑处理，发现OH-和H2O+离子在阳极附近比较密集，远离阳极密度就大幅减小，OH-离子的密度在t=35 ns时最大值达到了4.04×1018m-3，H2O+离子最大值达到了9.02×1018m-3；H-离子密度则有极大的波动，其密度最大值达到1.49×1018m-3。在仿真模型中，H-与OH-的电子碰撞反应及参考反应分别是R25与R26，其电压阈值分别是3.28 V与4.36 V，小于H2O+参考反应R6的电压阈值13 V，H+与OH-被先电离，在同等电场相同能量下，能量被消耗后抑制H2O+的电离，使其密度小于H+和OH-的密度。但是仿真结果发现H2O+的密度远大于OH-的密度，原因是H+在R28、R29、R42与OH-在R30、R31的化学反应部分被消耗，从而使两者密度降低。

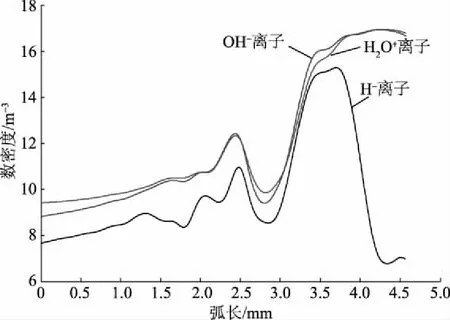
图10 t=35 ns时离子分布对数表示Fig.10 Ion distribution logarithm as t=35 ns

本文电晕放电中有关H2O的反应有22种，故会产生很多相关的粒子，而其中对绝缘子有严重影响的2个重要粒子分别是OH-离子和OH自由基。由图11可以看出在潮湿环境下，2种粒子在绝缘子金属部位(阳极)附近的密度很高，而这2种粒子都会加速绝缘子的腐蚀。其中OH-会加速绝缘子的腐蚀的原因有2点：①OH-在水参与下失去电子得到H+和O2，其中H+离子在电场的作用下会向阴极迁移，使OH-密度高处的氧气的含量较高；②绝缘子与外电源相连接的是锌材料，失去电子的Zn+离子与附近密度较高的OH-离子发生氧化还原反应，生成氢氧化锌[23]。OH自由基则是大气中一种重要的氧化剂，所以高密度的OH自由基自然会加速绝缘子的氧化。

图11 t=35 ns时绝缘子正极附近表面离子分布Fig.11 Surface ion distribution near the positive pole of the insulator as t=35 ns

3 结论

本文提出了在潮湿条件下绝缘子表面电晕放电特点，考虑了H2O对电晕放电的影响，研究了电晕放电的几大显著特征，分析了与仅有N2与O2环境下电晕放电的不同，讨论了在水分子参与下放电中产生的2种重要粒子。得到的结论如下：

a)在潮湿环境中，放电区域空间电子密度、电势与电场强度的发展规律与干燥环境下的发展规律极为相似，而其中电子密度的发展情况有着明显的不同，在绝缘子伞裙的附近电子密度要远低于干燥环境中的。在潮湿环境中，电子易附着在水分子上形成离子团，使得电子崩的作用减弱，伞裙表面附近的空间电子密度远低于干燥空气下的。

b)在潮湿环境下，电子温度明显大于干燥环境下的，说明了尽管水分子减小了电子崩的作用，但是放电区参与的化学反应更多，并且电离系数随相对湿度的增加而增大，电子与空气中水分子发生的碰撞电离次数增加，电离区等离子反应增强，从而电子的温度增大。

c)由于水分子的参与，潮湿环境下绝缘子正负两极的OH-和OH自由基密度明显提高，绝缘子金具腐蚀更为严重。

d)在水分子的参与下，潮湿环境中电子与水分子的碰撞使电离阈值电压部分低于干燥环境下的，而反应速率部分高于干燥环境下的，从而在相同的反应时间内抑制N2与O2相关粒子的产生。