基于切换理论的三机电力系统控制器设计

吕晶剑，孙丽颖

基于切换理论的三机电力系统控制器设计

吕晶剑，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州 121001）

电力系统中的发电机发生严重故障或需要检修时会被迫退出系统，当故障消除或检修完成时，又会重新回到系统。针对这两种情况发生后的系统稳定性问题，建立三机互联电力系统的切换数学模型。利用Lyapunov函数法和backstepping法，实现切换系统的切换励磁控制器设计。然后通过多Lyapunov函数法，证明三机互联电力系统切除或增加发电机的过程中，闭环系统是稳定的。最后通过仿真进行了验证。

切换系统；三机电力系统；backstepping法；多Lyapunov函数

电力系统是一个多维、复杂的非线性系统。随着我国科技的发展，对电力系统安全稳定运行的要求也越来越高。如何找到合适的方法保证电力系统安全稳定运行，是当下所面临的难题。

切换系统是由一组连续或离散的子系统组成的，按照某种切换规则在各个子系统之间进行切换的动态系统[1]。电力系统稳定是指系统受到扰动后能够重新获得运行平衡点，且系统可以在该平衡点处稳定运行的能力[2]。扰动可以有多种，在这里把扰动分为两类：自然因素、人为因素。自然因素包括线路老化造成某电力部件功能丧失，雷击造成保护装置跳闸，线路跳闸等；人为因素包括维护过程中操作人员将发电机、线路切除或加入等。将扰动前和扰动后的系统分别视为两个子系统，那么这两个子系统就组成了一个切换系统，则可以用切换系统理论进行电力系统稳定性研究。

近几十年来，人们将切换理论应用到诸多领域，并且取得了许多成果。文献[3]在给定切换信号的情况下，通过设计控制器选择机制，来保证切换发生时不同的子系统可以对应合适的控制器，从而达到稳定控制的目的。文献[4]研究一类纯反馈的非线性系统，基于多Lyapunov函数和backstepping法设计控制器，设计切换律，然后将此方法应用于非线性系统含有不确定性的情况中。文献[5]采用共同Lyapunov函数法，设计控制器，保证切换双机系统的稳定性，但是并没有考虑切换律的设计。文献[6-7]针对切换双机电力系统带有干扰和不确定的情况，利用共同Lyapunov函数设计控制器，证明闭环系统的稳定性。

将基于三机电力系统模型，采用多Lyapunov函数[9]和backstepping法，对三机切换电力系统进行控制器设计，给出切换律，证明闭环系统的稳定性，最后通过仿真验证所设计控制器的有效性。

1 系统模型

针对3台发电机组成的电力系统，图1为切换三机电力系统接线图[8]。

图1 三机电力系统接线图

建立三机电力系统的数学模型如下[10]：

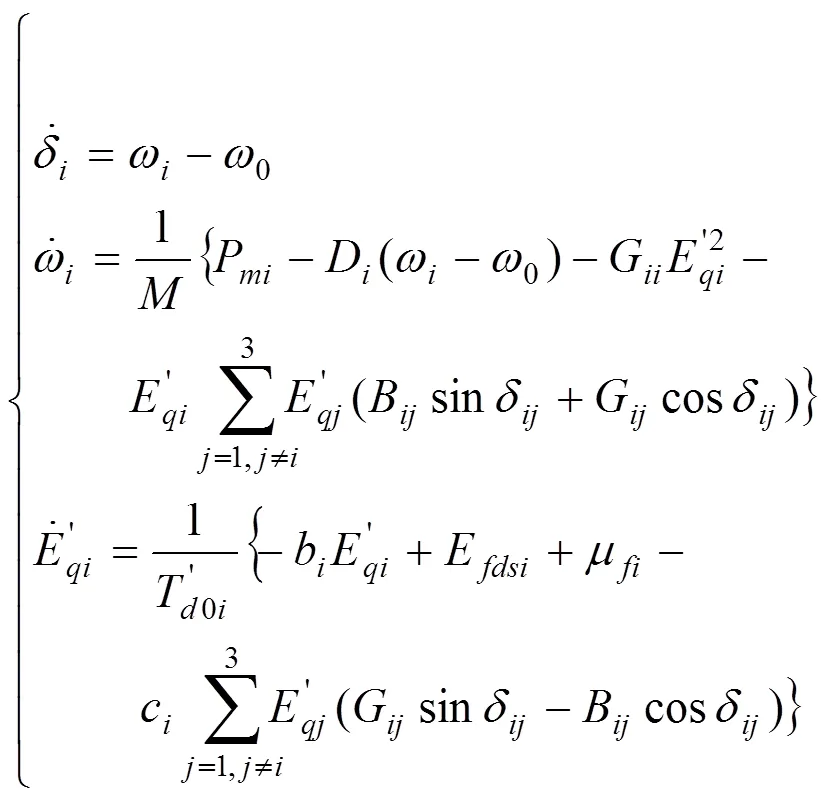
建立非线性切换模型，发电机被切除后可以表示为：

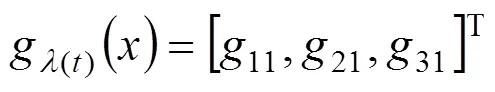
其中：

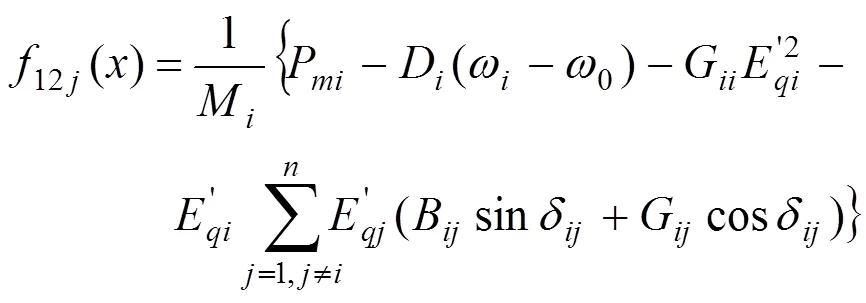
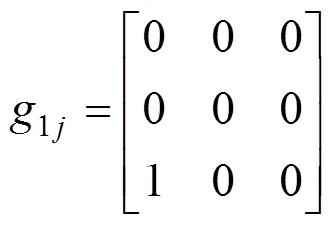
通过以上化简可以得到三机互联电力系统的非线性数学模型如下：

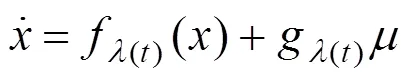
考虑三机互联电力系统：

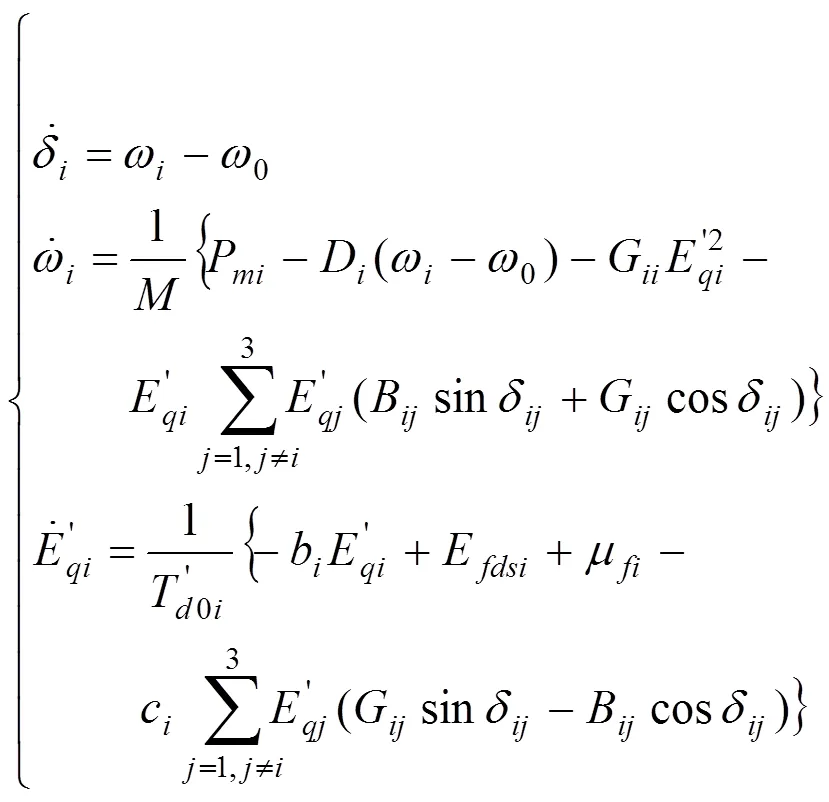
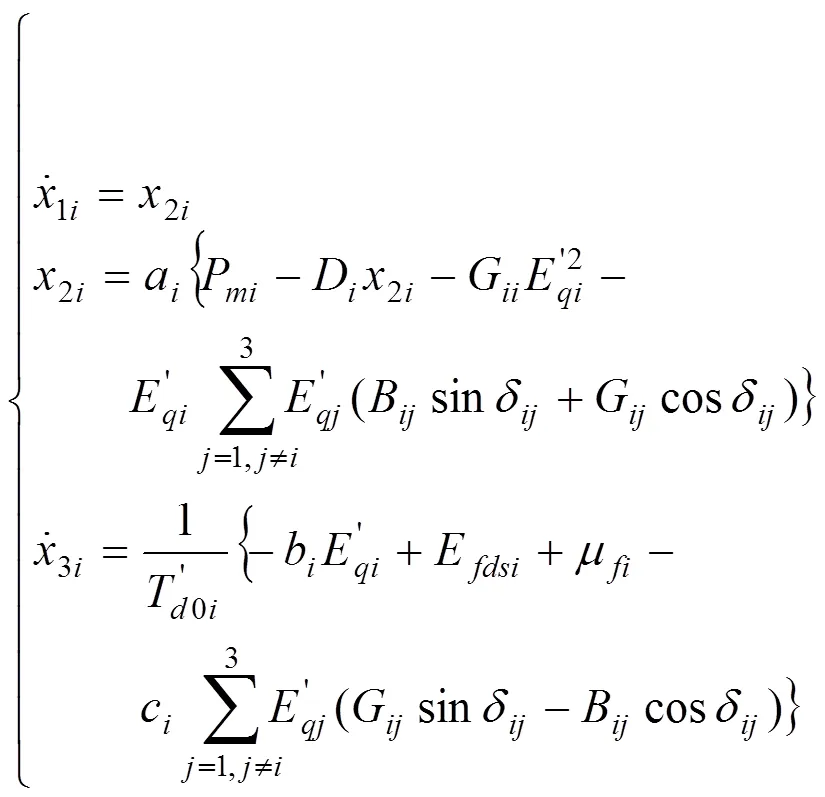
假设：(1)紧急情况发生时或者维护期间，1号、2号、3号发电机任意1台停止工作，紧急情况消失或维护完成后，停止工作的发电机再次加入运行。(2)紧急情况发生时或者维护期间，1号、2号、3号发电机任意2台停止工作，紧急情况消失或维护完成后，停止工作的发电机再次加入运行。(3)不管发生什么情况，最多有2台发电机退出系统。(4)3台发电机的平衡点相同或者差距很小。

基于以上假设一共可以分为7种情况，分别为1号发动机退出或加入系统，2号发动机退出或加入系统，3号发动机退出或加入系统；1、2号发动机退出或加入系统，1、3号发动机退出或加入系统，2、3号发动机退出或加入系统，发动机1、2、3号同时运行。由于这几种情况大致相仿，在这里主要讨论3号发电机退出系统然后又回到系统中和2、3号发电机退出和回到系统中，三机切换系统的稳定性问题。

基于以上假设，得到当3台发动机同时运行时的子系统1为：

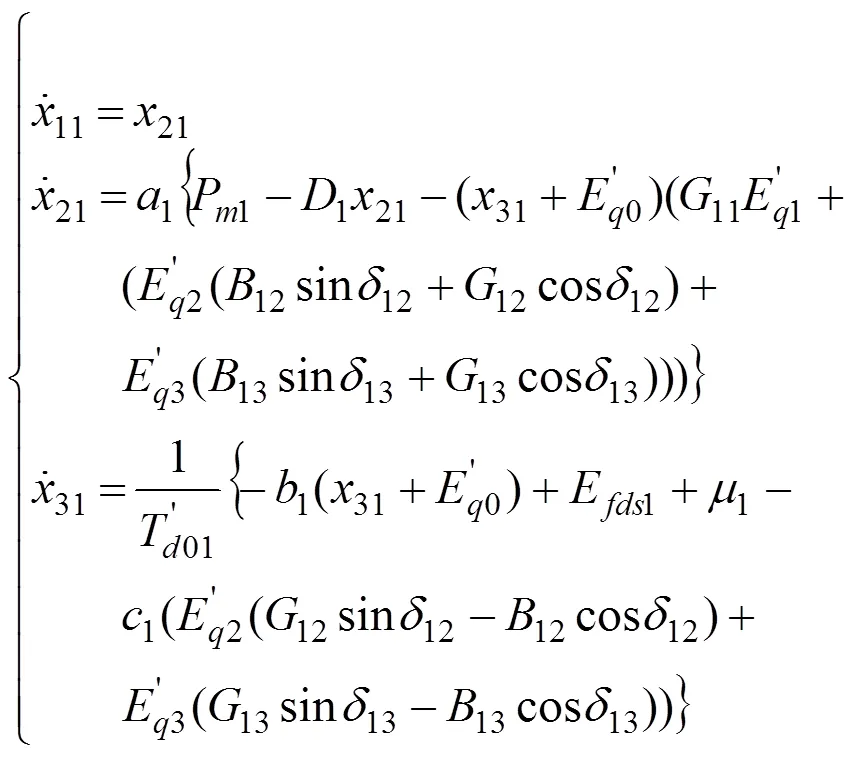
式(5)~(7)分别为子系统1中1号、2号、3号发动机的数学模型。

当3号发电机退出系统后，子系统2为：

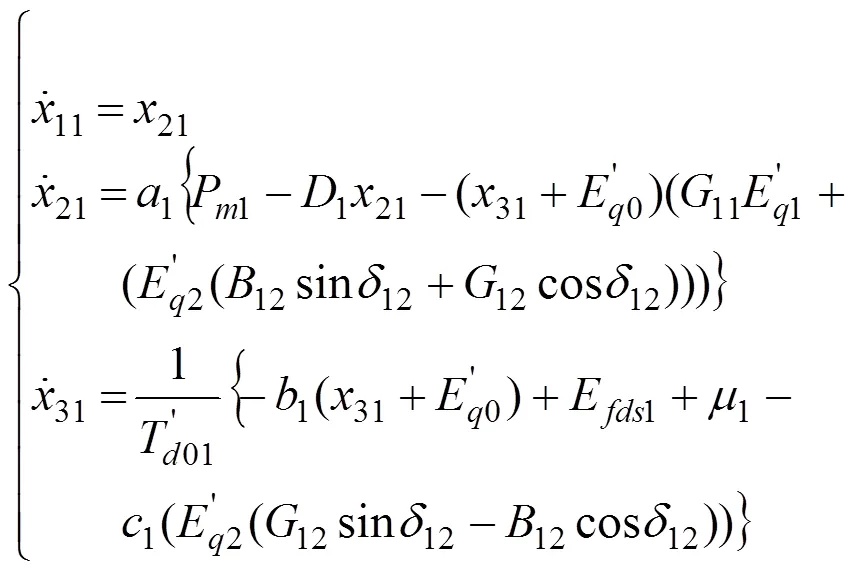
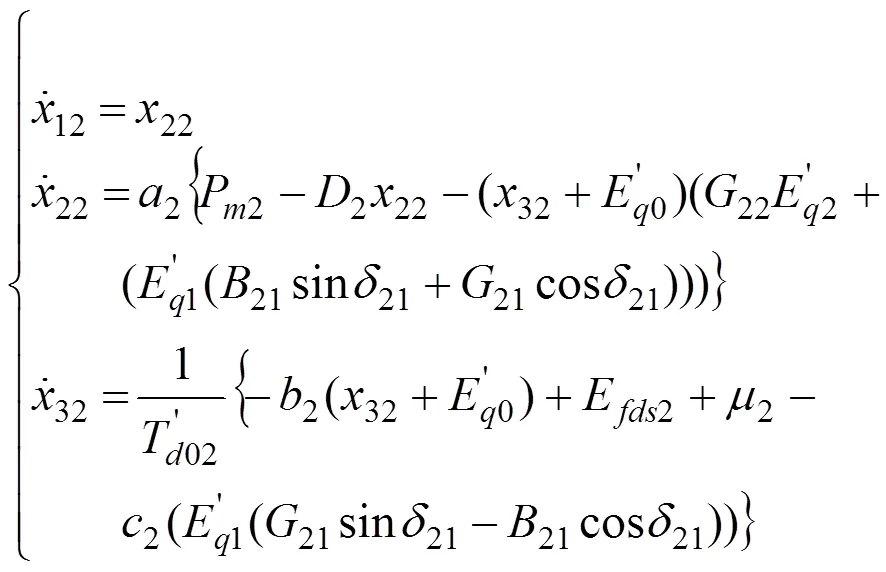
式(8)、(9)分别为子系统2中1号和2号发动机的数学模型。

2号3号发电机退出后，子系统3为：

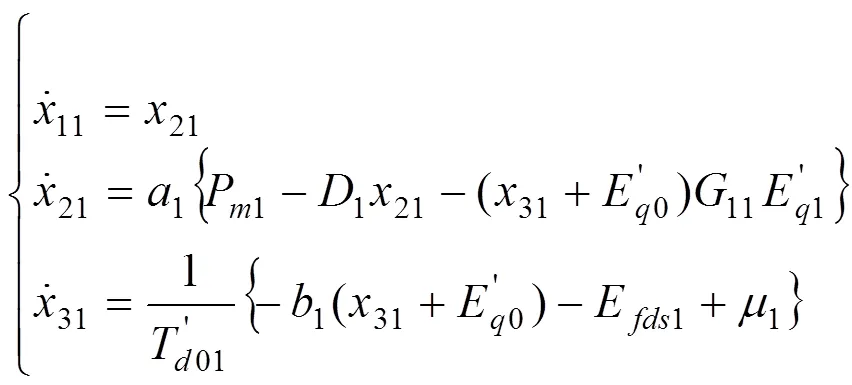
式(10)为子系统3中1号发动机数学模型。

控制目标：忽略阻尼不确定性对系统的影响，设计励磁控制器和切换律，调节发电机的相对功角，相对转速和相对暂态电势稳定运行于某平衡点。

2 子系统控制器设计

2.1 子系统1

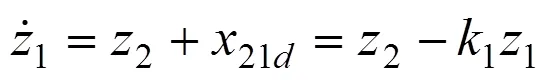
令系统(5)的第一阶Lyapunov函数为：

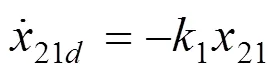
第二步 对式(11)进行增广，如下式：

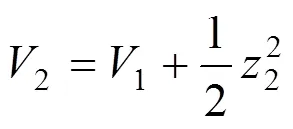
注意到：

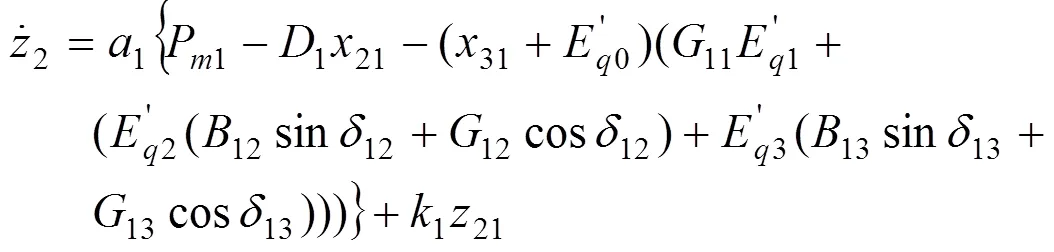
式(12)对时间的导数为：

令：

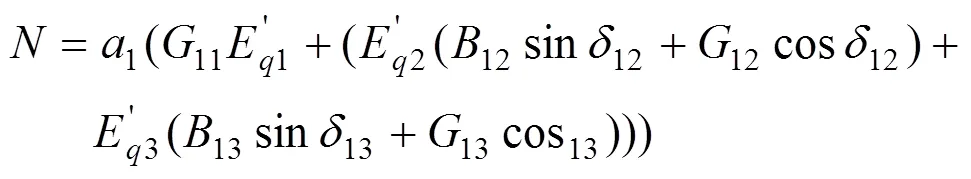
取新的镇定函数：

由此可得：

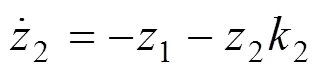
第三步 对(12)进行增广形成系统的全局Lyapunov函数为：

注意到：

式(13)对时间的导数为：

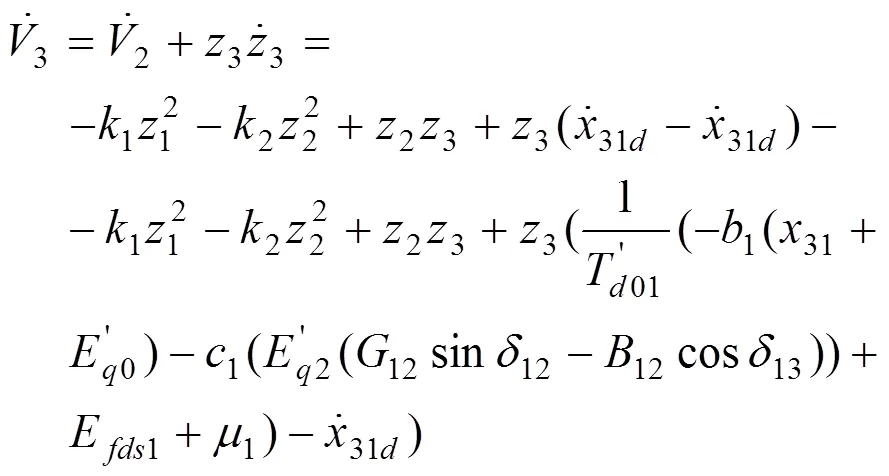
选择控制律：

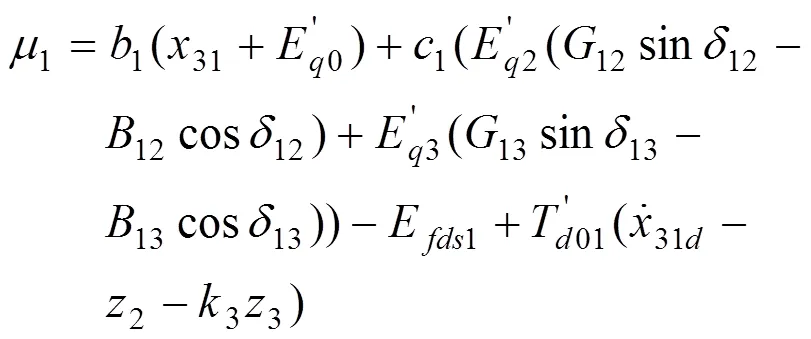
在反馈控制律(14)的作用下，子系统1中1号发动机的闭环误差系统为：

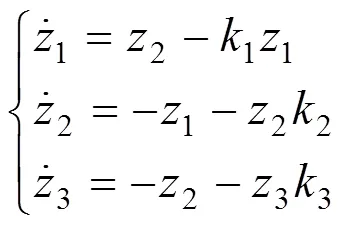
同理可以得到2号发电机的控制律和闭环误差系统如下：

(16)

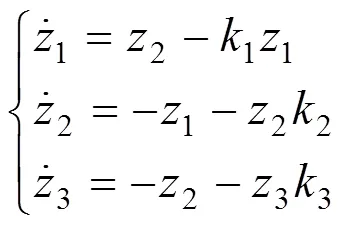
对于子系统2和子系统3，可以使用相同的方法进行设计，这里只给出设计结果。

2.2 子系统2

1号发电机控制律为：

闭环误差系统：

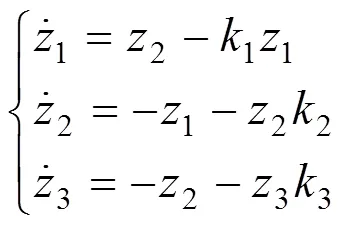
2号发电机控制律：

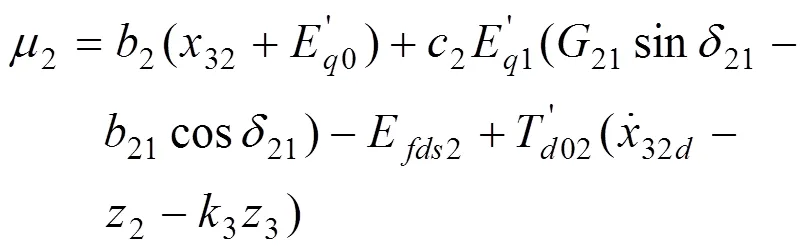
闭环误差系统：

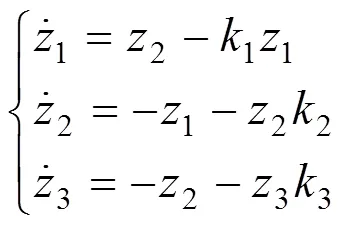
2.3 子系统3

1号发电机控制律：

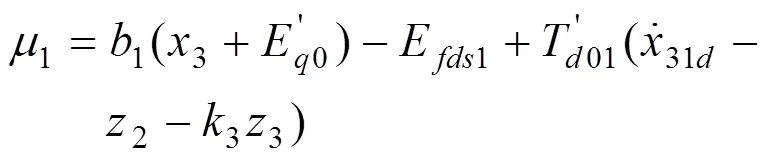
闭环误差系统:

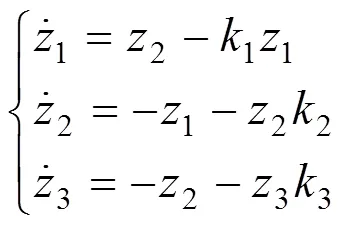
从式(15)、(17)、(19)、(21)、(23)可以看出，切换子系统对应的闭环误差系统是相同的。从所得控制律的表达形式看，系统中运行的发电机越多，受互电导和互电纳的影响，控制器的结构越复杂。

3 稳定性分析

考虑非线性切换系统：

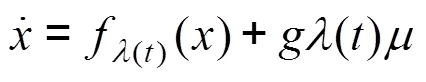
定义1 多Lyapunov函数法：对于任意一个子系统，如果下一次激活时的Lyapunov函数的终点值（或起点值）小于上一次被激活时Lyapunov函数的终点值（或起点值），那么系统能量呈现衰减趋势，则系统全局渐近稳定[5]。

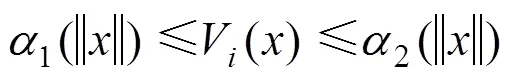
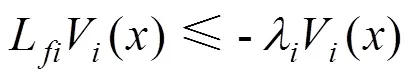
那么切换系统是渐近稳定的。

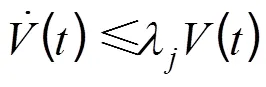
等价于：

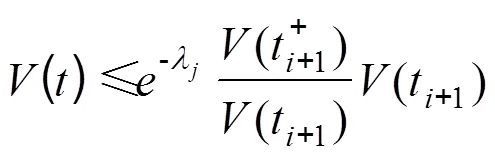
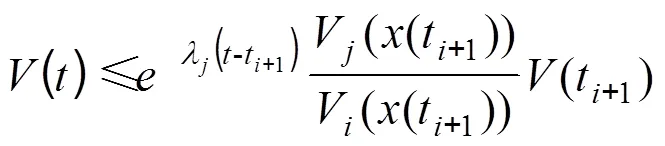
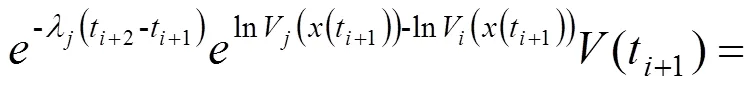
又由式(27)得：

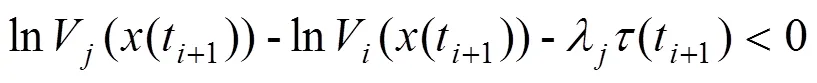
所以可以得：

式(30)符合定义1，切换非线性系统(24)渐近稳定，证毕。

4 切换律设计

假设一下两种情况：

由上文推论可知，假设1、2可以满足定义1，所以可以设计切换率如下：

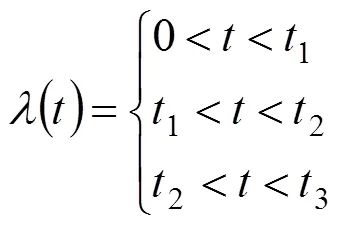
5 仿真研究

物理参数如下。

第一种情况：系统刚开始运行在子系统1，40s时发生故障切换到子系统2运行，故障清除后再次切换回子系统1运行。

仿真图如图2、图3。

图2 切换三机系统1号发电机状态响应曲线

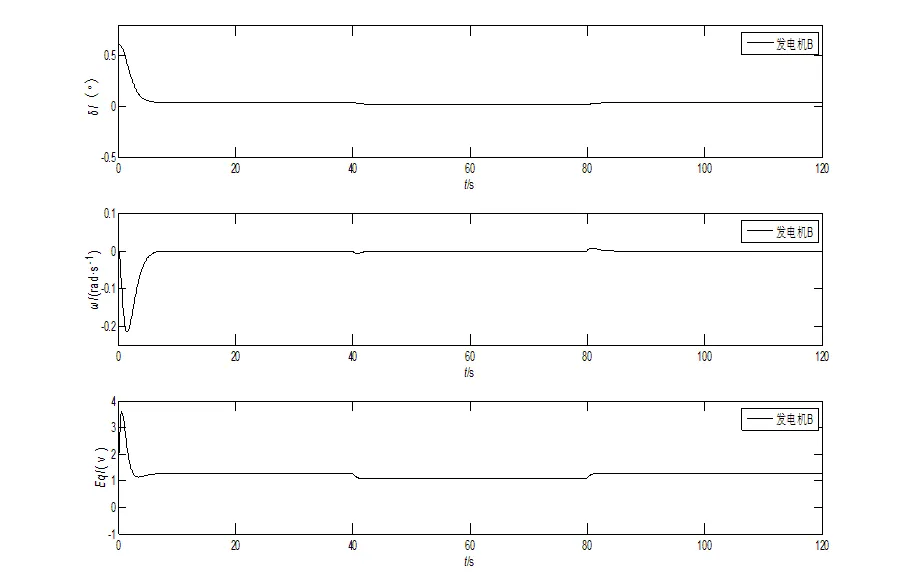
图3 切换三机系统2号发电机状态响应曲线

图4 切换三机系统1号发电机状态响应曲线

第二种情况：系统刚开始运行在子系统1，之后发生故障切换到子系统3运行，故障清除后再次切换回子系统1运行。

由仿真结果图2~图4的状态响应曲线可以看出，系统无论是切除发电机还是增加发电机，在控制器的作用下都可以在极短的时间内达到稳定，所以本文设计的控制器和切换律可以保证切换系统的稳定性。

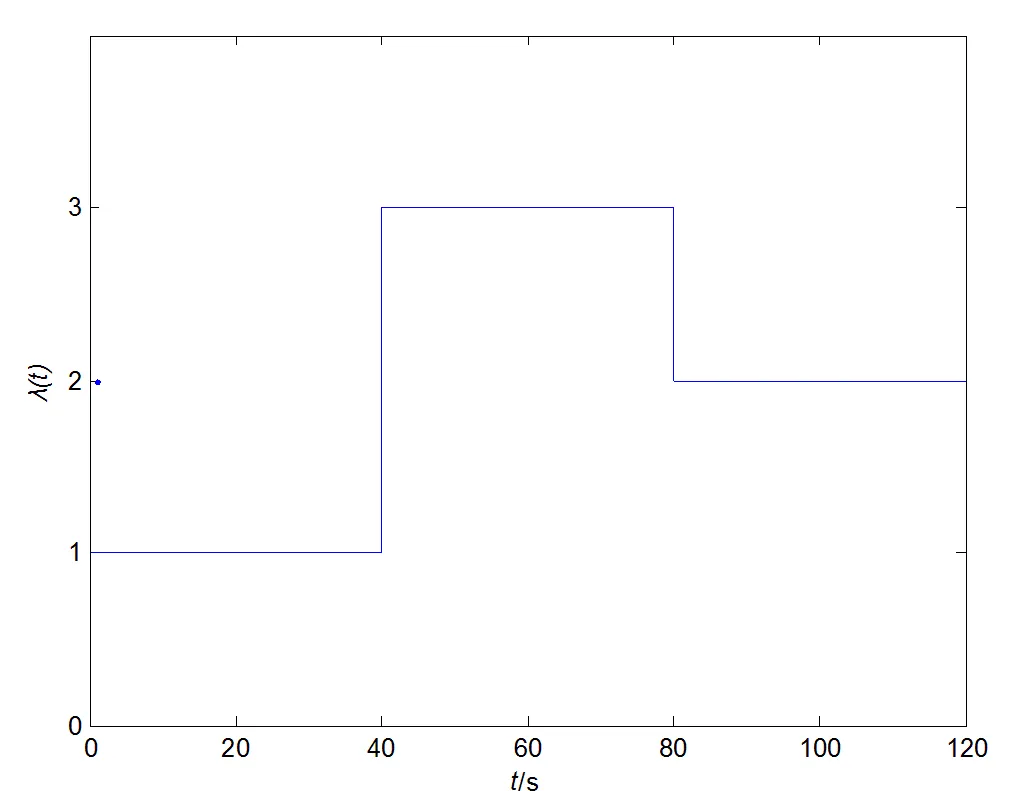
图5 切换信号

6 结论

研究了三机切换系统在发生切机操作时的稳定性问题，利用反步法设计子系统的控制器，用多Lyapunov函数法设计切换率，保证三机切换电力系统的稳定性。最后通过仿真证明结果的可行性。

[1] Decarlo R, Branicky M S, Lennartson B. Perspective and results on the stability and stabilizability of hybrid systems [J]. Procof IEEE, 2000, 88(7): 1069-1082.

[2] Kundur P, Paserba J, Ajjarapu V, et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions[J]. Power Systems, IEEE Transactions on, 2004, 19(3): 1387-1410.

[4] 向峥嵘, 向伟铭. 基于反步法的一类非线性切换系统控制器设计[J]. 控制与决策, 2007, 22(12): 1373-1376.

[5] 冯泉. 切换双机电力系统的稳定性研究[D]. 沈阳: 东北大学, 2009.

[6] 陈胜泉, 孙丽颖. 带干扰的切换双机电力系统鲁棒控制器设计[J]. 辽宁工业大学学报: 自然科学版, 2017, 37(1): 6-9.

[7] 切换双机电力系统的鲁棒控制器设计[J]. 西南民族大学学报: 自然科学版, 2014, 40(1): 115-119.

[8] 电力系统切换动态建模与励磁控制研究[J]. 郑州大学学报: 工学版, 2014, 34(6): 6-10.

[9] Liberzon D, Morse A S. Basic problems in stability and design of switched systems[J]. IEEE Control Systems Magazine, 1999, 19(5): 59-70.

[10] 电力系统非线性鲁棒控制[M]. 北京: 清华大学出版社, 2007.

Design of Three-machine Power System Controller Based on Switching Theory

LV Jing-jian, SUN Li-ying

（School of Electrical Engineering, Liaoning University of Technology, Jinzhou 121001, China）

When the generator in the power system has serious fault or needs to be repaired, it will be forced to exit the system. When the fault is eliminated or the repair is completed, it will return to the system. Aiming at the system stability problem after these two situations occur, a mathematical model of switching the three-machine interconnected power system is established. The Lyapunov function method and the backstep method are used to realize the design of the switching excitation controller of the switching system. Then, through the multiple Lyapunov function method, it is proved that the closed-loop system is stable during the process of cutting off or increasing the generator of the three-machine interconnection power system. Finally, verification is performed by simulation.

switching system; three-machine power system; backstepping method; multiple Lyapunov functions

TM761

A

1674-3261(2020)01-0005-07

10.15916/j.issn1674-3261.2020.01.002

2019-06-25

辽宁省自然科学基金项目(2015020076)

吕晶剑(1994-)，男，山东省淄博人，硕士生。

孙丽颖(1972-)，女，辽宁抚顺人，教授，博士。

优先出版地址：http://kns.cnki.net/kcms/detail/21.1567.T.20191227.1017.004.html

责任编校：孙 林