卧式埋地罐土层压力计算方法研究

吴 皓

(中国石化工程建设有限公司，北京 100101)

卧式埋地罐常用于存储汽油、柴油、煤油、渣油等油品, 被广泛应用于油库、加油站、化工厂等场所，同地上卧罐相比，具有消防设施简单、有较强的防火防爆能力、节省土地资源、降低工程造价等特点。但是由于卧式埋地罐要承受土层压力，因此在设计中应充分考虑土层压力对设备安全的影响。目前国内相关的设计标准和规范还没有对这部分内容的明确规定。

土层对于埋地罐的影响主要体现在2个方面：

1) 土层覆盖于卧罐之外，对埋地罐附加外压作用；

2) 土层重量作为均布载荷作用于埋地罐，使鞍座承受的载荷和壳体中的应力增大。

在埋地罐设计中应考虑以上两者的影响并进行相关计算与设计。

1 现有埋地罐土层压力计算方法

根据土力学基础【1】，距离地面深度为H的截面处竖直土压力pv为：

pv=γHgPa

(1)

式中：γ——土层密度,kg/m3；

H——离土层表面的深度,m；

g——重力加速度，m/s2，此处取值为9.81 m/s2。

在H深度上土层同时存在的侧向压力ph为：

ph=Kpv=KγHgPa

(2)

式中K为侧压系数，可根据土体内摩擦角φ计算获得【2】，即：

K=1-sin(φ)

(3)

对于埋地罐筒体上最大土层压力作用点的位置，目前国内的文献总体有两种看法【3】，一种认为埋地罐的最大压力在筒体顶部，基于式(1)和(2)有最大压力pmax为：

pmax=γH0gPa

(4)

式中：H0——筒体顶部到土层表面的距离,m。

另一种观点认为，埋地罐的最大压力出现在筒体水平轴对称平面以上1/3倍半径的位置【4】。这一结论主要依据挡土墙计算中土层作用力的作用点位于挡土墙下端以上1/3的位置【1】。因此筒体的最大压力pmax为：

(5)

式中：R——埋地罐筒体外半径,m。

以上两种计算方法从理论角度分析均存在问题。原因在于式(1)和式(2)都是基于均匀的土层，而当埋地罐存在时，会在土层内部增加新的边界条件，从而引起土层应力重新分布【5】，这将导致埋地罐附近土层的应力状态并不符合式(1)和式(2)。对于埋地管道周围应力分布的研究也表现出这一复杂性(见图1)【6】。

图1 埋地管道土层应力分布

英国工程师协会标准EEMUA-190【7】对埋地罐表面最大压力规定如下：

p0=G0/πRPa

(6)

式中：G0——筒体上部受到的土层重量载荷，N/m。

该方法是将筒体上的土层重量平均到半个圆周上作为筒体上的最大压力，但实际土压力在圆柱上表面并非均匀分布(见图1)，因此该方法得出的最大压力较低。

2 现有土层重量载荷计算方法

目前几种土层重量载荷计算方法的模型如图2 所示。图2(a)方法认为埋地罐上土层的重量载荷同筒体正上方的重量相关，因此单位长度上埋地罐上方的土层重量载荷为：

G0=(2HR-πR2/2)γg

(7)

由于筒体上方的土层在埋地罐边界上会发生滑移，因此筒体承受的土层重量理论上应大于正上方的重量，该方法对于重量的预估偏低。考虑到这一因素，图2(b)的方法认为筒体承受的是一个与内摩擦角相关的倒锥形区域内的土层重量，因此重量载荷可按式(8)计算：

G0=[2HR-πR2/2+H2/tan(φ)]γg

(8)

式(8)计算的筒体承受的土层重量载荷偏大，原因有二：一是实际土层的滑移角度并非为内摩擦角；二是土层滑移面为一斜面，滑移面上的重量由筒体和滑移面共同承担。对此EEMUA-190【7】对计算模型进行了修正[见图2(c)]，减小了倒锥形区域的面积，计算如式(9)所示：

G0=(2HR-πR2/2+H2/3)γg

(9)

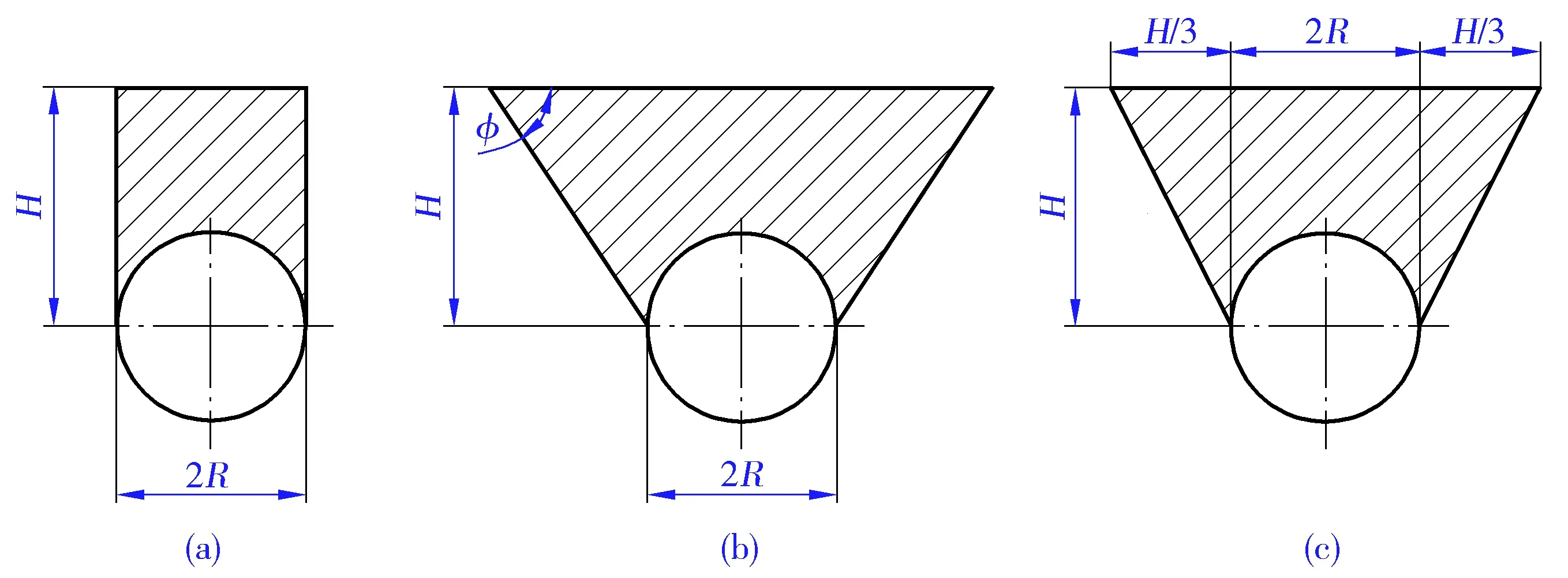
图2 土层重量模型计算示意

上述针对埋地罐土层外压和土层重量载荷的计算方法主要是基于挡土墙理论和埋地管道的研究结果，而直接针对埋地罐的研究很少。但埋地罐的边界情况和以上两种情况都存在较大的差别，目前的计算方法在工程设计中的适用性和可靠性都有待考察。因此本文采用ANSYS有限元软件和岩土力学方法，建立埋地罐计算模型，研究填埋高度、内摩擦角、填埋边界对埋地罐压力分布的影响，并将结果与现有计算方法进行对比分析，进而提出适合的土体外压和土体载荷计算方法，以期为埋地罐的工程设计提供依据。

3 计算模型

3.1 模型假设

为简化计算，采用二维模型对埋地罐土层压力开展研究，计算模型基于如下假设：

1) 埋地罐筒体足够长，可采用平面应变模型将埋地罐简化为二维模型；

2) 埋地罐筒体相对土体刚度足够大，可将埋地罐表面作为固定边界条件；

3) 埋地罐采用鞍座支撑，基础夯实，鞍座基础平面可作为固定边界条件。

埋地罐的填埋方式可以分为上埋式和沟埋式两种，各自模型的边界条件如图3所示。

3.2 土体模型

土体模型采用Mohr-Coulomb(MC)模型，该模型主要针对土壤、岩石混泥土之类的聚合材料。MC模型认为，土层颗粒在任意平面当剪切力满足式(10)时即会发生滑移。

图3 计算模型边界条件

τ=c-σmtan(φ)

(10)

式中：τ——切应力,Pa；

c——土的粘聚力,Pa；

σm——平均应力,Pa。

计算方法如下：

(11)

式中：σ1，σ2，σ3——分别为第一、第二和第三主应力，Pa。

由于埋地罐填埋一般选用砂土，故本文计算材料选为砂土。土体性质如表1所示。

表1 砂土的材料性质

建立ANSYS有限元模型如图4所示。

4 埋地罐土层压力参数影响分析

埋地罐的受力同填埋土体的性质和边界都有直接关系，本文主要针对以下计算工况开展不同参数条件(见表2)下埋地罐土层压力的分析。

图4 有限元模型

表2 计算工况与参数

4.1 填埋高度对土层外压的影响

以工况1为例进行填埋高度对土层压力影响分析。不同填埋高度下土层的压力云图见图5，筒体圆周上的压力分布见图6。

图5 工况1的不同填埋高度埋地罐土层压力分布

图6 工况1的不同填埋高度埋地罐圆周压力分布

由图5可以看出： 在土层压力作用下， 埋地罐筒体主要由上半圆承压。筒体上的压力最大点发生在上半圆两侧面一定角度(见图6)。这一点与文献【6】试验得到的压力分布趋势一致(见图1)， 同时也印证了本文方法的可靠性。当填埋高度较浅时， 顶部的压力相对较小， 上半圆土层压力分布不均匀性大， 在H0/R=0.2时，圆筒上的最大压力为顶部压力的5倍；随着填埋高度的增加， 圆筒顶部压力迅速增大， 上半圆压力分布差异减小， 在H0/R=4时， 整个上半圆压力水平已基本相同(见图6)。

H0/R=0.2时土层的压力矢量如图7所示。从压力矢量的方向可以看出：砂土土层在圆筒曲面边界上会发生一定的滑移，顶部和圆筒周围都倾向于向圆筒侧面流动。这也是导致侧面局部压力偏大的原因。而当H0/R=4时，由于填埋比较深，在圆筒上部一定距离会形成一个三角形滑移区[见图8(a)]，土体滑移发生重叠，从而对整个上表面都产生作用，使得顶部压力随之增加。

图7 H0/R=0.2土层压力矢量

图8 H0/R=4土层压力矢量

4.2 内摩擦角对土层压力的影响

内摩擦角为42°时的计算结果如图9和图10所示。由图9和图10可以看出，其不同填埋高度结果变化规律同工况1类似。当H0/R<2时，工况1和工况2的压力水平相差不大；当H0/R≥2时，随着填埋高度增加，工况2的压力水平比工况1明显增加(见图10)。与内摩擦角为32°时的情况相比，圆筒在内摩擦角为42°时受到竖直方向上的土层分压更大。

4.3 填埋边界对土层压力的影响

在很多情况下，埋地罐是放置于沟道或防渗池中的，这时边界离筒体较近，会对埋地罐的压力分布产生影响。本文采用工况3边界探讨填埋边界对土层压力的影响。

图11为不同填埋高度埋地罐土层压力分布，图12为工况3的不同填埋高度埋地罐圆周压力分布，将图11和图12的结果同前述工况1和工况2的结果进行对比，可以看出：沟埋方式的埋地罐筒体侧向压力比上埋方式的要小，这与边界限制了土体的滑移运动有关。由图11(c)、图11(d)和图12 可以看出：当H0/R较大时，筒体正上方的压力较大，且相比其他两种工况，整个上表面压力分布更为均匀。

5 结果分析与对比

5.1 土层压力

将上述数值计算结果同式(4)～式(6)所示的3种压力计算方法的计算结果进行对比，如表3所示。

将表3中的pmax/γgR数值计算结果同公式计算结果对比可以看出：式(4)与式(6)的结果与数值计算结果存在较大偏差；式(5)的结果比数值结果偏低但总体趋势上基本吻合。

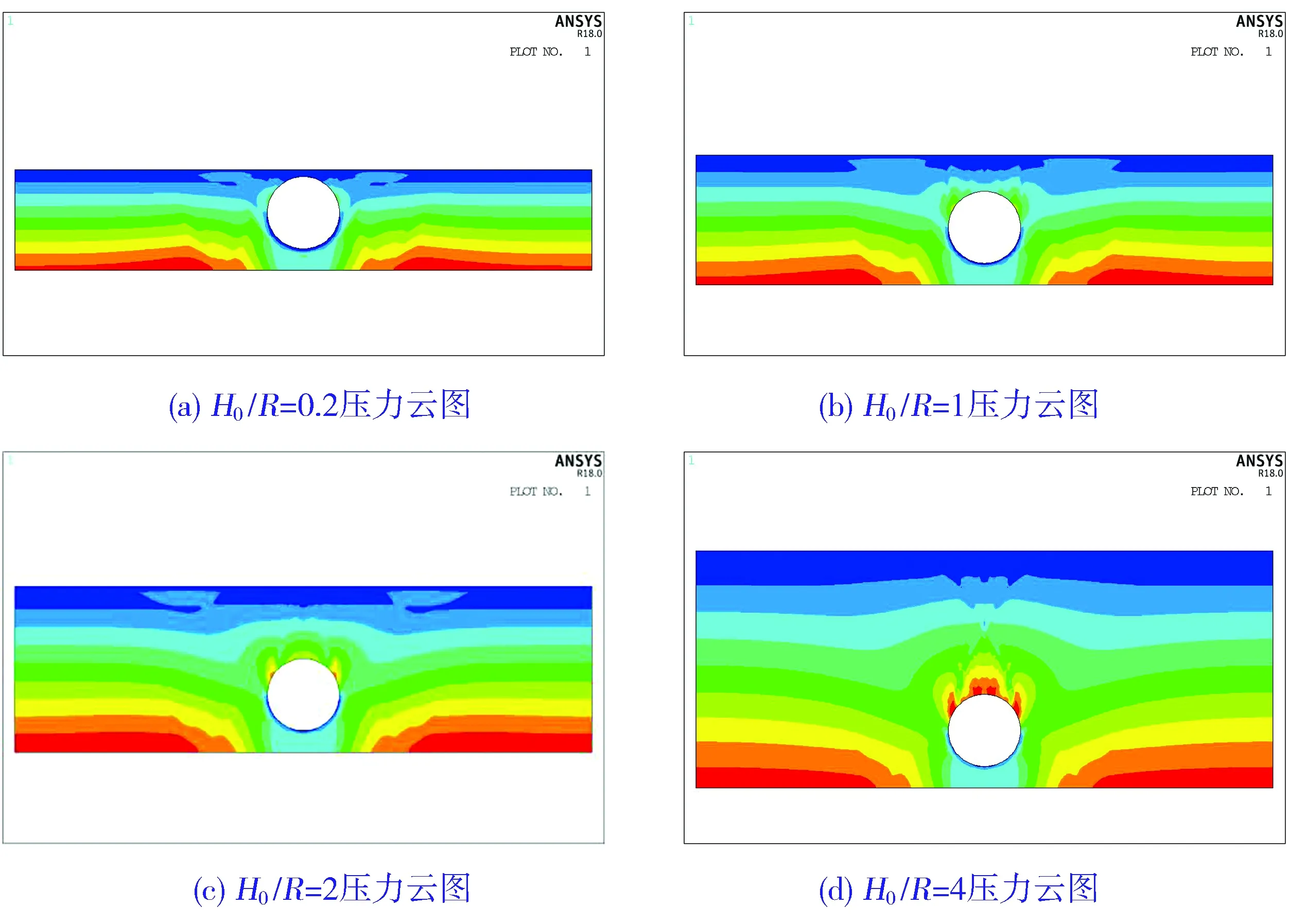
图9 工况2的不同填埋高度埋地罐土层压力分布

图10 工况2的不同填埋高度埋地罐圆周压力分布

根据以上结果可知，现有的计算公式对于埋地罐表面最大压力的预估都存在不同程度的偏低的问题，应用于设计不够安全。

基于本文的数值方法计算结果，现提出外压计算式(12)：

(12)

式中：k1——修正系数，根据数值计算结果并考虑工程安全裕量,可取1.7～2.0。

图11 工况3的不同填埋高度埋地罐土层压力分布

5.2 土层重量载荷

可在数值计算模型中提取筒体边界受到的总合力来评估筒体承受的土层重量载荷，获得的计算结果如表4所示。其中Fy为筒体承受的竖直力总和，Fx为筒体单侧承受的水平力总和。G、G1和G2分别为采用式(7) ～ 式(9)计算得到的土层重量载荷。

对比不同工况下Fy和Fx的计算结果可知：内摩擦角小时，水平力相对较大；内摩擦角大时，竖直力相对较大。这一结果与内摩擦角小时侧压作用大的判断一致[式(3)]。对于沟埋条件， 由于筒体两侧边界作用明显， 筒体受到的竖直力和水平力都比较高。

图12 工况3的不同填埋高度埋地罐圆周压力分布

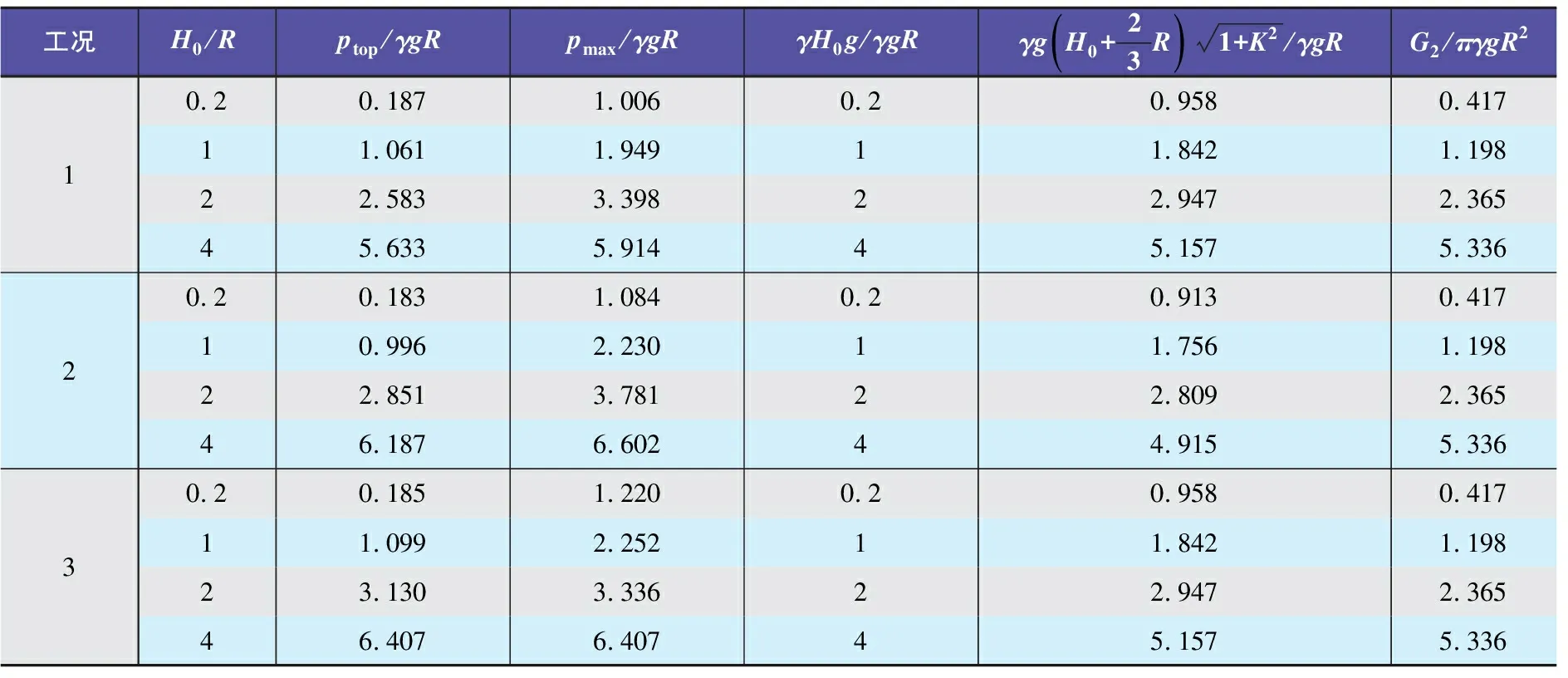
表3 土层压力计算结果对比

注：表3中ptop为数值计算的筒体顶部压力(Pa)，pmax为数值计算的筒体表面的最大压力(Pa)。

表4 土层重量计算结果对比

随着填埋高度的提高，筒体Fy/G并非是线性变化，这与埋地罐周围土体滑移规律发生变化有关。埋土较浅时，土层滑移为顶部和圆筒周围的砂土都向圆斜面滑动(见图7)。随着填埋高度增加，顶部形成三角滑移区，两侧土滑移均覆盖整个圆筒上部，使得土层对圆筒作用压力趋于平均化。由于工程中埋地罐的H0/R通常介于该滑移规律变化过程中，这就导致埋地罐土体载荷变化规律存在复杂性。因此，在设计中应保留一定裕量以考虑上述不确定性。

从表4可以看出：式(7)和式(8)的计算结果相比数值计算结果存在较大程度的偏离，式(9)的计算结果同数值计算结果基本吻合。

据此，提出式(13)以计算埋地罐承受的土体重量：

G0=k2G=k2(2HR-πR2/2)γg

(13)

式中：k2——修正系数，考虑安全裕量建议取2.0～2.4。

6 结论

采用岩土力学和数值分析方法对填埋土为砂土的不同参数条件下的埋地罐模型开展了研究，主要得到如下结论：

1) 不同填埋高度H0/R下筒体表面压力分布规律不同，H0/R<2时， 筒体圆周上压力分布不均匀性大， 最大压力同顶部压力最大差别可达5倍；H0/R≥2时， 筒体上方压力总体趋向于均匀。

2) 埋地罐承受的土体重量随内摩擦角增大而增大，水平总压力随内摩擦角增大而减小。

3) 沟埋条件下筒体表面压力分布相对于上埋条件更为均匀，且压力水平更高。

4) 埋地罐在不同H0/R下的土体载荷变化规律复杂，对土体载荷进行计算时应考虑足够的裕量。

5) 目前对于埋地罐承受的土层压力和土层重量的计算方法存在非保守和过保守的情况，本文在数值计算的基础上提出了工程适用的计算公式。