基于周期间歇策略的复杂网络随机同步定

马慧慧,何秀丽

(河海大学 理学院，江苏 南京 211100)

0 引言

复杂网络是具有复杂拓扑结构和动力行为的大规模网络，由大量的节点通过边的相互连接构成.在过去的几十年里，复杂网络在生物科学、电力系统、计算机世界等领域中得到了广泛的应用[1,2].在复杂网络研究中，复杂网络动力学行为的研究是神经网络理论成功应用的前提，因而受到学者们的普遍关注.

复杂网络中的每个节点相互影响、相互连接、相互耦合，构成一个网状结构,各子节点根据其它系统的状态来调整自己的状态，使得它们的动力学性质表现出某种关系，用动力学的术语就称为同步.同步现象在自然界中普遍存在，比如萤火虫的同步发光，钟摆的同步摆动等等.研究同步不仅能帮助人们理解这些自然现象和行为发生的内在机理，还能通过同步原理来实现无人机编队表演、合作型群体机器人的开发等任务.近十年来，为实现网络的同步定，众多新颖的控制策略被采用，如间歇控制[3-7]、牵制控制[4,5]、自适应控制[6]、有限时间控制[7,8].其中间歇控制策略能够减少控制器长时间工作产生的磨损,进而延长控制器的工作寿命和减少控制成本，因此成为研究热点.

众所周知，现实世界中不可避免的出现随机噪声，为了更精准的刻画现实世界，Yang X等[9]学者开始研究随机复杂网络的同步控制问题.自Hasminskii R[10]指出噪声可以镇定一个不稳定的系统后，噪声的作用也逐渐被认识，Mao X[11]和黄礼荣等[12]学者系统的研究了随机镇定理论.Russo等[13]首先尝试利用噪声实现复杂网络的同步定.

2019年，Liu L等[14]将间歇控制策略和随机镇定理论整合，针对一般系统建立了间歇随机镇定的充分性判据.复杂网络具有独特的结构特征和清晰的应用背景，因此基于复杂网络的结构特征建立间歇随机同步定判据具有理论意义和应用价值.据作者所知，基于间歇随机镇定策略的复杂网络的同步定尚未被研究，本文的研究动机就是填补这一空白.

1 预备知识

首先，考虑模型

(1)

其中xi(t)=(xi1,xi2,…,xin)T是第i个节点的状态变量，f:Rn→Rn是非线性函数，正常数c是耦合强度，正定矩阵Γ=diag(r1,r2,…,rn)表示节点的内联矩阵，G=(aij)N×N是网络的结构矩阵，其中元素定义如下：如果从节点j到节点i(i≠j)有一个定向连接，那么aij=1,否则

在此基础上，考虑使用周期性间歇控制来镇定复杂网络系统,得到基于周期间歇控制的复杂网络模型为

σh(t)Γ(s(t)-xi(t))dB(t)

(2)

其中

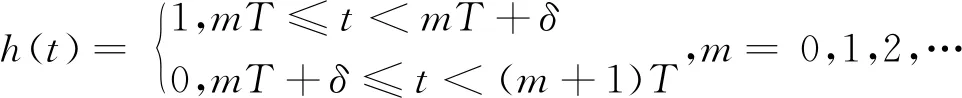
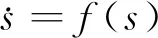
对于非线性函数f，做出如下假设：

假设1存在一个常数θ>0，对于∀x,y∈Rn，使得非线性函数f满足：

(x-y)T(f(x)-f(y))≤θ(x-y)TΓ(x-y)

(3)

2 主要结论

定理1令假设1和λmax(Γ)≤2λmin(Γ)成立，若噪声强度σ和间歇率ψ满足

(1-ψ)σ2>2λmax((θIN-cL)⊗Γ)·

(4)

那么系统(2)是几乎必然指数稳定的，即系统(1)可被随机同步定.

证明：对于某个节点的状态变量xi(t)，有

σh(t)Γ(s(t)-xi(t))dB(t),

m=0,1,2,….

设ei(t)=xi(t)-s(t),则

dei(t)=(f(t,xi(t))-f(t,s(t))-

(5)

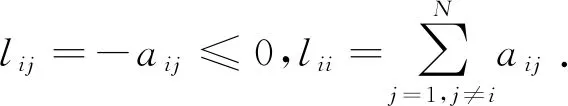
F(t,x)=(fT(t,x1),…,fT(t,xN))T,

则(5)式可改写为

de(t)=(F(t,x(t))-IN⊗f(t,s(t))-(cL⊗Γ)e(t))dt-h(t)((σIN⊗Γ)e(t))dB(t)

(6)

设V=log(|e(t)|2),

(cL⊗Γ)e(t))dt-h(t)((σIN⊗Γ)e(t))dB(t)}+

由假设1可得

h(t)((σIN⊗Γ)e(t))dB(t)}+

(7)

同时注意到

e(t)(θIN-cL)⊗Γ)e(t)≥

λmax(θIN-cL)⊗Γ)|e(t)|2,

所以

dV≤2λmax((θIN-cL)⊗Γ)dt+

(8)

当t∈[0,δ)，

dV≤2λmax((θIN-cL)⊗Γ)dt+

(9)

可得

log(|e(t)|2)≤log(|e(0)|2)+

(10)

其中

由(10)可得

log(|e(δ)|2)≤log(|e(0)|2)+

log(|e(0)|2)+δ(2λmax((θIN-cL)⊗Γ)+

(11)

当t∈[δ,T),有

log(|e(t)|2)≤log(|e(δ)|2)+

(12)

由(12)可得

log(|e(T)|2)≤log(|e(δ)|2)+

log(|e(0)|2)+δ(2λmax((θIN-cL)⊗Γ)+

(T-δ)(2λmax((θIN-cL)⊗Γ))+M(T)=

log(|e(0)|2)+δa1+(T-δ)a2+M(T)

(13)

其中

a2=2λmax((θIN-cL)⊗Γ).

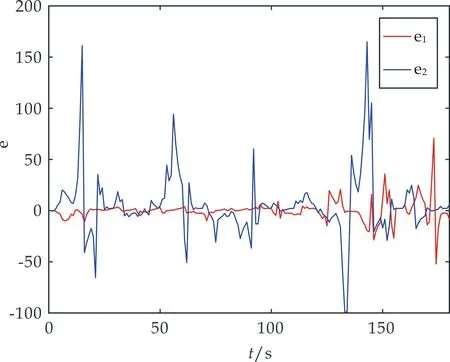
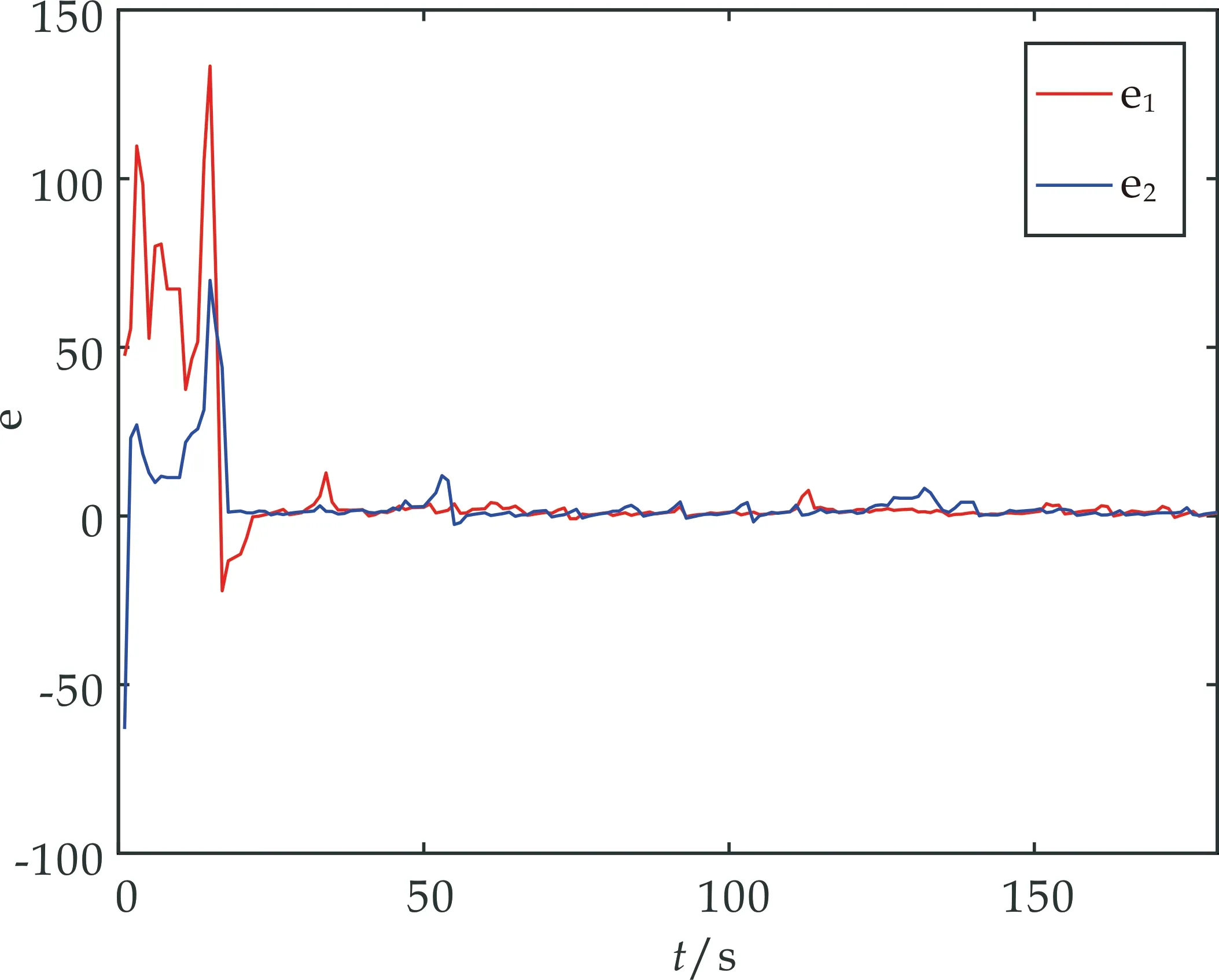
当mT≤t

log(|e(t)|2)≤log(|e(0)|2)+mδa1+

m(T-δ)a2+(t-mT)a1+M(t)=

(t-mT)a1+M(t)

所以

log(|e(t)|2)≤log(|e(0)|2)+

(ma1(1-ψ)+ma2ψ)T+(t-mT)a1+M(t)

(14)

当mT+δ≤t<(m+1)T，

log(|e(t)|2)≤log(|e(0)|2)+mδa1+

m(T-δ)a2+δa1+(t-mT-δ)a2+M(t)=

log(|e(0)|2)+(ma1(1-ψ)+ma2ψ)T+

δa1+(t-mT-δ)a2+M(t)

(15)

易证

〈M(t),M(t)〉=

由鞅大数定律，可得

(16)

两边同时取上极限可得

a1+ψ(a2-a1).a.s

(17)

由λmax(Γ)≤2λmin(Γ)和

(1-ψ)σ2>2λmax((θIN-cL)⊗Γ)·

证毕.

注1在文献[4]和文献[10]中，刘锡伟、杨鑫松等人研究了基于间歇策略的复杂网络同步定.本文将间歇策略和随机同步定结合，并证明了复杂网络的周期间歇随机同步定.

注2文献[14]研究了基于随机反馈的复杂网络同步定，相比于文献[14]，本文进一步利用周期间歇噪声实现复杂网络的同步定.

3 数值例子

考虑复杂网络(2)，相应的取值如下

当ψ=0.2、σ=0.3,系统的误差状态曲线如图1所示；当ψ=0.8、σ=0.68,系统的误差状态曲线如图2所示；当ψ=0.2、σ=0.68,系统的误差状态曲线如图3所示.

图1 ψ=0.2,σ=0.3时系统误差的状态曲线

图2 ψ=0.8,σ=0.68时系统误差的状态曲线

图3 ψ=0.2,σ=0.68时系统误差的状态曲线

注3对比图1和图3可知，间歇率相同的情况下，强度较大的噪声可以更好的镇定系统；对比图2和图3可知，噪声强度相同的情况下，较小的间歇率可以更好的镇定系统.

4 结论

本文研究了复杂网络的周期间歇随机同步定.首先，结合复杂网络的结构特征设计了周期间歇随机镇定控制器.其次，通过使用Ito公式、鞅大数定律等随机分析工具，结合间歇控制策略特点，建立了复杂网络随机同步定的充分性判据.最后，通过数值仿真验证了判据的有效性.