流固耦合对裸露输气管道固有频率的影响

马 青,赵子龙

(太原科技大学 应用科学学院,太原 030024)

埋地管道在石油、天然气等长距离输送领域得到广泛应用。在工程实际应用中,由于流体介质与管道系统的相互作用,使管道产生振动。管道系统的耦合振动将导致振动噪声污染,严重的耦合振动将导致管系结构损坏、管内介质外泄,甚至会引发爆炸等严重事故,给社会造成极大隐患。

国内外学者针对管道振动问题做出大量研究,谭平[1]等人针对外部激励作用下的振动问题进行了分析;任建亭[2]等人建立了输液管道线性、非线性动力学模型,并利用有限元模型进行分析;李长俊[3]等人建立了输气管道振动系统微分方程;TingyueHao[4]等人建立了简支约束下埋地管道的横向自由振动微分方程;张立翔、黄文虎[5]等人利用水动力学对输流管道流固耦合振动进行了研究;杨晓辉[6]等人详细的描述了采空区埋地管道的沉降变形;李琳[7]等人分析了管道系统流固耦合振动的研究动态;M.Fu-Iu、Y.Xiaoming[8]建立了埋地输流管道系统的振动的动力学模型;V.P.Feodosiev[9]对输流管道振动的稳定性做了详细研究;王世忠[10]等人推导出输送流体管道的固液耦合振动方程,求解出输水管道在不同边界条件下的临界速度和固有频率。

然而,对于考虑管内气体压力造成的流-固耦合及温度对输气管道横向振动的影响这类问题,还没有出现详细的描述。因此对这种现象进行分析研究,有利于管道系统的合理设计和管理,有利于提出更可靠的防振措施。

1 管道横向振动微分方程的建立

1.1 系统的能量

(1)系统的总动能

在考虑流体可压缩性、管内流体线密度可变性的基础上,对管道动能和流体动能进行分析,得到系统总动能。

T=TP+Tf=

(2)系统的总势能

管道势能包括管道弯曲产生的势能以及温度变化产生的势能,管道势能和流体势能的总和为系统总势能。

T=TP+TF=

1.2 横向振动微分方程

推导出在考虑了弯曲变形、流体压力和温度变化的下管道系统横向振动微分方程:

(1)

2 管道固有频率及临界流速分析

以简支管道为例,利用里兹法求解该管道振动系统的固有频率,其位移边界条件可表示为:

设满足上述边界条件的解为:

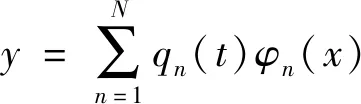
(2)

式中:qn(t)=q为广义坐标向量,φn(x)为振型函数(又称试函数),N为模态阶数。

将式(2)代入式(1)中,整理得到:

(3)

其中：“·”表示对时间t求偏导数,“′”表示对x求偏导数。

设简支管道中的振型函数为:

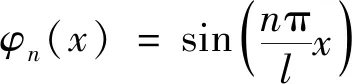
(4)

(1-2μ)(AFp+EAFαΔT).

将上式化简并整理,可得方程组

(5)

式中：q=[q1(t),q2(t),…,qn(t)]T为广义坐标向量。

C=[cnm]N×N为广义阻尼矩阵,矩阵中各元素为:

K=[knm]N×N为广义刚度矩阵,矩阵中各元素为:knm=

再将函数(4)代入上述三个矩阵元素,化简可得到:

由式(5)可得固有频率为：

由上式可得流体的临界流速为：

3 实例计算与分析

管道材质为X60(L415)钢管,管内输送的流体为天然气,其基本参数如表1所示。

表1 管道和流体基本参数表
Tab.1 Basic pipeline and fluid parameters

弹性模量E=210GPa管材密度ρp=7860kg/m3流体体积模量K∗=7.1MPa泊松比μ=0.3管材热膨胀系数α=1.2×10-5流体密度ρf=0.8kg/m3

根据表1提供数据和推导出的管道固有频率公式,利用MATLAB编程可分别得到管道几何参数、流体参数及温度改变量对管道各阶固有频率的影响。

3.1 流体对固有频率的影响

选取温度改变量分别为0 ℃、10 ℃、20 ℃,裸露长度l=15 m,壁厚t=10 mm,内径d=488 mm的管道,分别研究流体流速及压力对管道固有频率的影响。

3.1.1 流速

当管内流体压力为3.08 MPa,考虑工程实际中的流体流速,取值为0～30 m/s时,流速对输气管道前三阶固有频率的影响如图1所示。

由图1可得,管内流体流速对管道前三阶固有频率的影响较小,在该流速及温度变化范围内,均可忽略流体流速的影响。

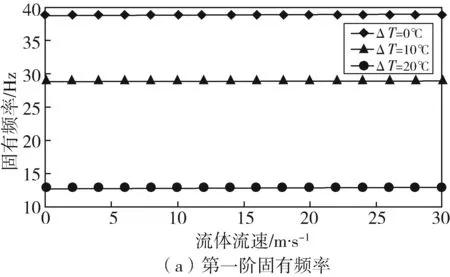
图1 流体流速对管道固有频率的影响曲线

3.1.2 流体压力

当管内流体流速为10 m/s,考虑工程实际中的流体压力,取值为0～6 MPa时,压力对输气管道固有频率的影响如图2所示。

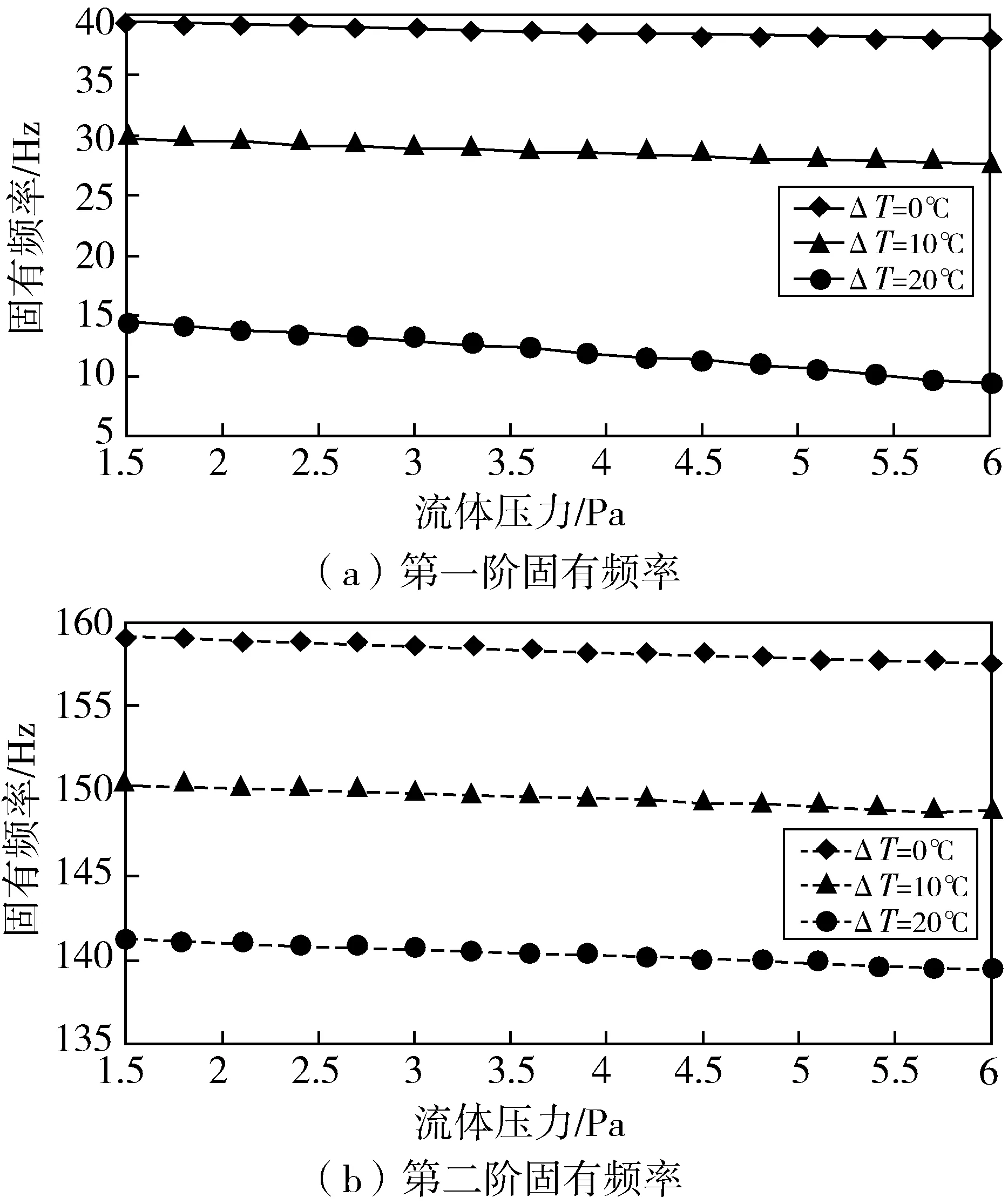
图2 流体压力对管道固有频率的影响曲线

由图2可得,管道固有频率随流体压力的增加而降低;温度改变量越大,固有频率随流体压力的变化越明显。

3.2 管道几何尺寸对固有频率的影响

当管内流体压力p=3.08 MPa,流速V=10 m/s时,分别考虑管道长度和外径因素对固有频率的影响。

3.2.1 管道长度

选取温度改变量分别为0 ℃、10 ℃、20 ℃,壁厚t=10 mm,管道内径d=488 mm,考虑工程实际中的管道长度,取值为10～20 m时,长度对输气管道固有频率的影响如图3所示。

由图3可得,管道固有频率值随管长的增加而降低;温差越大,固有频率随管长的变化越明显。对于较长的管道,当管道温度变化较大时,第一阶固有频率等于零,说明此时管道发生屈曲,在工程中要避免这种情况发生。

3.2.2 管道外径

选取温差分别为0 ℃、10 ℃、20 ℃,管道长度l=15 m,壁厚t=10 mm的管道,考虑工程实际中的管道外径,取值为0.2～1 m时,管道外径对输气管道固有频率的影响如图4所示。

由图4可得,管道固有频率随外径的增加而增加;温差越大,固有频率随外径的变化越明显。对于较细的管道,当管道温度变化较大时,第一、第二阶固有频率等于零,说明此时管道发生屈曲,在工程中要避免该情况发生。

3.3 温度改变量对固有频率的影响

在流体压力p=3.08 MPa,流速为V=10 m/s环境下,选取管道裸露长度分别为10 m、15 m、20 m,壁厚t=10 mm,管道内径d=488 mm的管道,当温度改变量在0～30 ℃范围时,温度改变量对输气管道固有频率的影响如图5所示。

图3 管道长度对固有频率的影响曲线

图4 管道外径对固有频率的影响曲线

图5 温度变化量对管道固有频率的影响曲线

由图5可得,管道固有频率随温差的增加而降低,管道越长固有频率随温差的变化越明显。

4 结论

(1)管内流体流速对管道固有频率的影响较小,工程流速范围内,可忽略流体流速的影响。

(2)管道固有频率随流体压力的增加而降低;温度改变量越大,固有频率随流体压力的变化越明显。

(3)管道固有频率值随管长的增加而降低,随外径的增加而增加;温度改变量越大,固有频率随外径的变化越明显。

(4)管道固有频率随温度改变量的增加而降低,管道越长固有频率随温度改变量的变化越明显。

(5)管道较长或温度变化量较大都会导致管道屈曲失效,在工程实际中要避免该情况的发生。