基于熵理论和RBF神经网络的有源压制干扰识别方法

彭荣硕 董鹏曙 孟藏珍

(空军预警学院 武汉 430019)

0 引言

近年来，电子技术发展迅猛，电子干扰机的性能大大提高，使得有源干扰可在极短时间内对探测到的雷达信号进行压制、调制与转发，对雷达产生有效干扰[1-3]。然而，目前国内对于复杂电磁环境下的干扰识别技术还处于相对初级阶段，在如何识别有源干扰，采取何种抗干扰手段，如何选取参数等方面都主要依靠操作员的经验，具体数据和理论支撑不够完善严谨，具有较大不确定性和模糊性，不利于形成稳定的可持续提升的战斗力。

目前，国内外学者针对有源压制干扰自动识别问题不懈努力，发表了大量研究成果。文献[4]针对FRFT域，提取盒维数和信息维数作为特征参数来描述压制干扰和高斯白噪声的分形特征，并以此识别压制干扰，但由于采用FRFT，因此计算量较大；文献[5]基于三种常规压制干扰在功率谱上与白噪声的差异，计算相关系数，并用门限检测方法识别干扰信号，但由于主要针对高干信比(Jamming-to-Noise Ratio, JNR)条件下设置门限，因此低JNR时识别率较低；文献[6]提取了雷达受干扰角度特征，雷达受干扰强度特征，干扰机径向距离特征，干扰机速度特征值，干扰机俯仰特征值，基于最大隶属原则，通过模糊综合评判判别干扰方式，但由于雷达受干扰强度特征需要通过操纵员人工判定，因此无法做到全自动化。

本文针对有源压制干扰的识别问题展开研究，在研究以上文章不足的基础上，提出了基于熵理论的有源压制干扰识别方法，利用3种有源压制干扰在频谱上的差异，提取干扰信号频谱的信息熵、指数熵以及范数熵特征，并使用神经网络进行识别，仿真结果表明，3种熵特征作为识别有源压制干扰的特征参数能取得较好的识别效果。相较于文献[4]、文献[5]和文献[6]，本方法仅需进行FFT，因此计算量较小，且分类器采用神经网络，低JNR条件下识别率较高，特征参数无需人工判定，自动化程度较高。

1 压制干扰分析建模

1.1 射频噪声干扰

利用直接噪声放大法，即使用射频功率放大器，放大通过带通滤波器的高斯白噪声信号，即可产生射频噪声干扰信号。尽管射频噪声干扰信号的性质与白噪声近乎一样，对雷达的干扰效果极好，但由于其功率受射频功率放大器的制约，因此功率一般不大，因此实际使用不多。射频噪声干扰信号数学表达式为

J(t)=Un(t)cos[ωjt+φ(t)]

(1)

式(1)中，ωj为载频；φ(t)为相位，且满足在[0,2π]上为均匀分布；包络Un(t)服从瑞利分布，且与φ(t)相互独立。

高斯白噪声通过0～20MHz的带通滤波器产生的射频噪声干扰的时域波形与功率谱波形如图1所示。

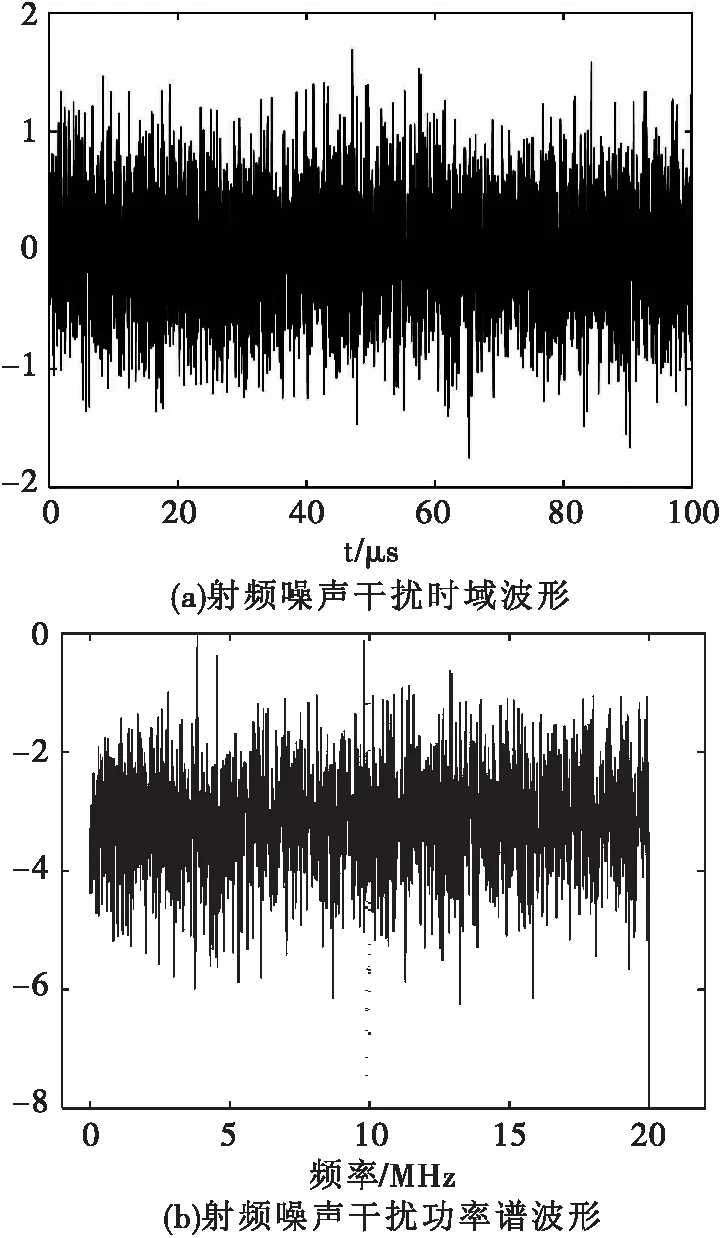
图1 射频噪声干扰时域波形与功率谱波形

1.2 噪声调频干扰

利用随机基带信号调制载波信号的频率，而其幅度不变，即可得到噪声调频干扰信号。由于噪声调频干扰信号包络起伏小，因此其效率高，是目前最为常用的有源压制干扰信号。噪声调频干扰信号数学表达式为

(2)

式(2)中，Uj为被调制信号幅度；ωj为载频；KFM为噪声调频信号的调制参数，表征频率的变化快慢；u(τ)为调制噪声，φ为初始相位且二者相互独立。

中心频率为10MHz，噪声调频斜率为100MHz/V的噪声调频干扰的时域波形与功率谱波形如图2所示。

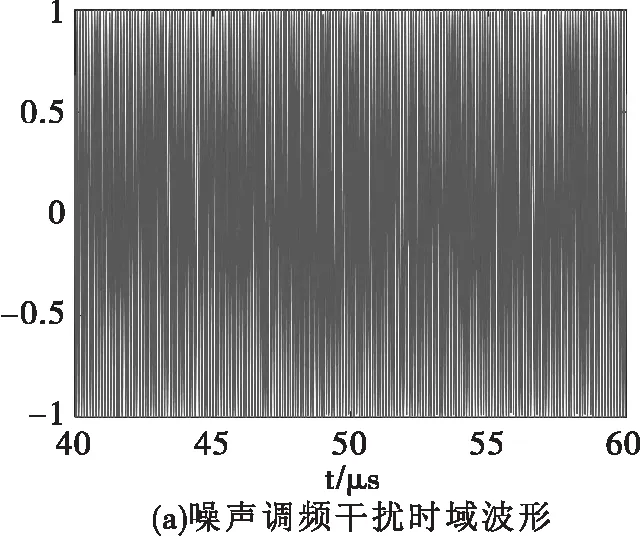
图2 噪声调频干扰时域波形与功率谱波形

1.3 噪声调幅干扰

与噪声调频信号相反，利用随机基带信号调制载波信号的幅度，而其频率不变，即可得到噪声调幅信号。由于噪声调幅干扰信号频谱较窄，因此一般用于瞄准式干扰，功率一般也不高。噪声调幅干扰信号数学表达式为

(3)

式(3)中，U0为被调制信号幅度；Un(t)为调制噪声，一般为带限高斯白噪声；KAM为噪声调幅信号的调制参数；ωj为载频；φ为相位，满足在[0,2π]上为均匀分布，且与Un(t)相互独立。

中心频率为10MHz，调制度为0.5的噪声调幅干扰的时域波形与功率谱波形如图3所示。

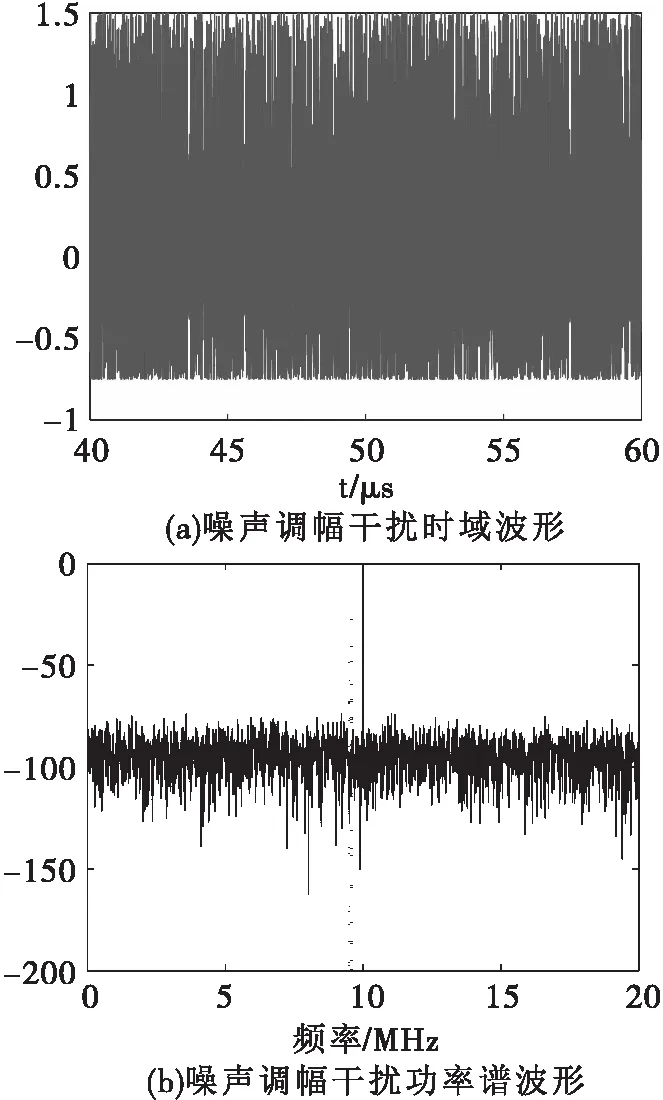
图3 噪声调幅干扰时域波形与功率谱波形

2 熵特征

熵最早是热力学系统中的一个概念，用来度量一个热力学系统的混乱度。之后，随着研究的深入，熵的概念在各个领域均得到不同的应用，其概念不断得到引申，但它用于表示系统的杂乱度等无序状态的用途始终如一。

2.1 信息熵

在信息熵理论[8]中，一条信息中的信息量，与其不确定性成正比，因此信息熵与信息中的信息量成正比。信号与噪声共同组成了雷达的接收信号，因此雷达即使接收两次同样的信号，但是受噪声的影响，信号也不完全相同，具有不确定性，因此可用信息熵来进行描述这种不确定性。将一个信息源中信号xi出现的概率定义为p(xi)，则信息熵H的数学表达式为

(4)

在不确定性问题上，信息熵无疑是一个有力且简便的工具，但其在实际应用中，却存在一定的缺陷。若一个信息源中信号xi出现的概率p(xi)趋近于0，按照定义，设ΔI(·)表示信息熵增量，则有ΔI(p(xi))→∞，然而在p(xi)=0的情况下，则ΔI(p(xi))=-ln(p(xi))是没有定义的，因此在实际应用中可能出现不收敛的情况。

2.2 指数熵

为了解决信息熵不收敛的问题，Pal等人[9]创造性地提出用1-p(xi)代替1/p(xi)，即为指数熵

(5)

通过式(5)可知，若一个信息源中信号xi出现的概率p(xi)=0，按照定义，指数熵的增量也为0，这就从原理上解决了信息熵可能不收敛的缺点，且由于用指数代替了对数，运算速度也可得到提升。

2.3 范数熵

不同干扰信号的脉内调制方式不同，其频谱有所区别，经张葛祥等人研究发现范数熵可用于定量描述信号的能量分布情况[10]。

设信号X={x(i),i=1,2,…,n}，则范数熵的数学表达式为

(6)

式(6)中，1

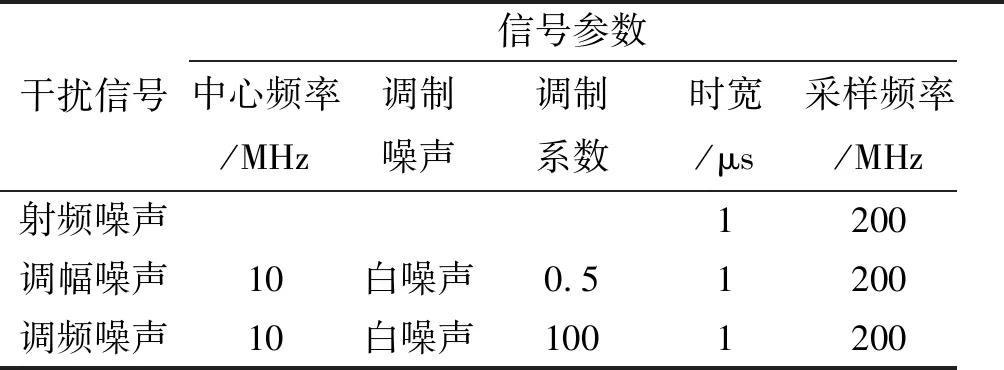
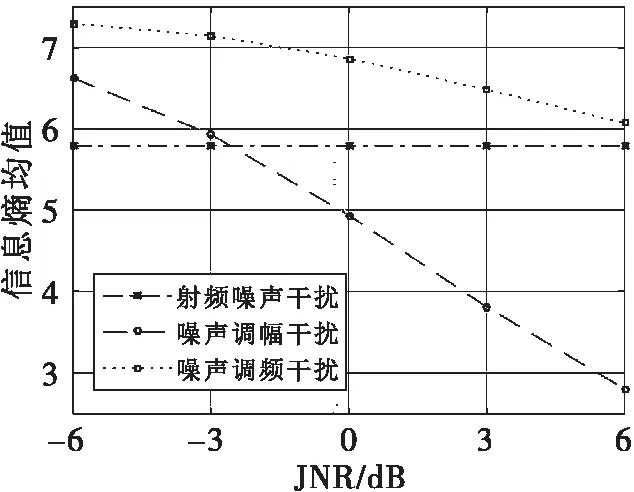
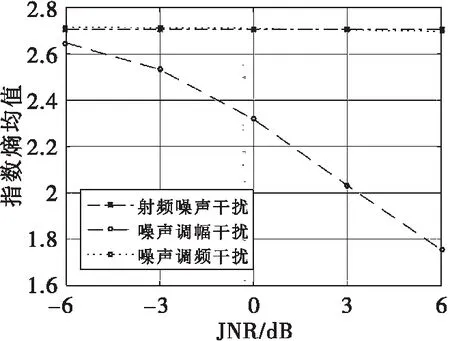
2.4 熵特征提取方法

本文利用3种有源压制干扰信号在频谱上的差异，提取信号的信息熵、指数熵以及范数熵，构建3维熵特征空间，用以描述不同干扰信号的频谱的不确定性，其提取流程如下：

1)对3种有源压制干扰信号进行FFT变换，将信号从时域变换到频域；

2)对频谱幅度归一化处理，并求出范数熵R；

3)计算单个频点的能量，并计算其占总能量比例，即为p(xi)；

4)利用p(xi)计算信息熵H和指数熵S。

3 仿真与分析

本文的仿真软硬件平台如下：MATLAB R2016a；Windows10x64；Intel Core i5-8400；NVIDIA GeForce GTX 1050 Ti。

为了检测3种熵特征在有源压制干扰识别中的性能，设置仿真参数如下：调制噪声为白噪声，方差σ2为1；JNR变化范围为-6dB～6dB，每3dB做500次蒙特卡洛仿真，分别计算3种有源压制干扰的信息熵、指数熵、和范数熵，并取均值；压制干扰参数设置如表1所示。

表1 干扰信号仿真参数表

干扰信号信号参数中心频率/MHz调制噪声调制系数时宽/μs采样频率/MHz射频噪声1200调幅噪声10白噪声0.51200调频噪声10白噪声1001200

经仿真后得到的3种熵特征随JNR的变化情况如图4-图6所示。

图4 信息熵随JNR变化曲线

图5 指数熵随JNR变化曲线

图6 范数熵随JNR变化曲线

从图中可看出，射频噪声干扰的3个熵特征均基本不随JNR改变，而指数熵和范数熵对噪声调幅干扰有较高的区分度，虽然范数熵在JNR趋近于0dB时难以区分射频噪声干扰和噪声调频干扰，但信息熵在此区间对二者有较高的区分度。通过以上分析可知，3种不同的压制干扰有不同的熵特征曲线，因此可用熵特征来对有源压制干扰进行识别。

为了验证熵特征在有源压制干扰识别方面的有效性，选用径向基函数(Radial Basis Function，RBF)神经网络对3种干扰信号进行分类识别。RBF神经网络性能优良，具有无局部极小问题，聚类分析能力强，学习算法简单方便且具有全局逼近能力等优点。

RBF神经网络有三种学习方法：一是自组织选取中心学习方法；二是直接计算法；三是有监督学习算法。本文选择有监督学习算法，通过训练样本集来获得满足监督要求的网络中心和其他权重参数，经历一个误差修正学习的过程，采用梯度下降法，因此可将其视为BP神经网络的一种。

每种信号的JNR变化范围为-6dB～6dB，每3dB做500次蒙特卡洛仿真，得到每种信号每3dB各500个特征样本，每个特征样本包含3种熵特征各1个点，并将 3个熵特征构建为{H，S，R}特征空间，以提高识别率。随机选择其中300个征样本用于RBF神经网络训练，剩余200个征样本用于测试RBF神经网络，RBF神经网络的径向基函数的扩展系数取1.0，得到的识别率如图7所示。

图7 识别率随JNR变化曲线

从图7可知，熵特征做为特征参数用以识别有源压制干扰，效果显著，在低JNR的情况下，识别准确率仍能高于90%，而JNR大于3dB时识别准确率超过98%。

4 结束语

干扰类型识别是雷达进行针对性抗干扰的基础，本文针对有源压制干扰的识别问题展开研究，在充分研究有源压制干扰数学模型和信息熵、指数熵以及范数熵的基础上，提出基于熵特征的有源压制干扰识别方法，将3种熵特征构建成{H，S，R}特征空间，用于联合识别有源压制干扰类型，并通过仿真分析验证了其性能。通过仿真实验证明，熵特征在低JNR时即可达到90%以上的识别准确性，当JNR高于3dB时识别准确率高于98%。